2019-2020学年高中数学新人教A版选修1-1课件:第二章圆锥曲线与方程2.2.2双曲线的简单几何性质(29张PPT)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修1-1课件:第二章圆锥曲线与方程2.2.2双曲线的简单几何性质(29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 00:00:00 | ||
图片预览








文档简介
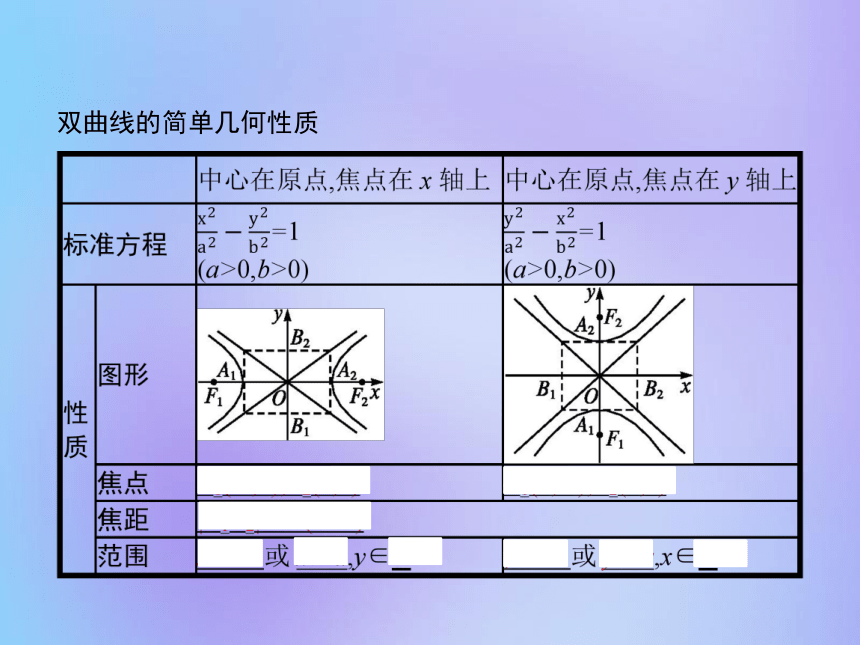
课件29张PPT。2.2.2 双曲线的简单几何性质双曲线的简单几何性质 解析:由于a2=16,b2=25,所以a=4,b=5,因此y0∈R,x0≥4或x0≤-4.
答案:(-∞,-4]∪[4,+∞) (-∞,+∞)【做一做3】 双曲线4x2-2y2=1的离心率等于 .?思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)双曲线的焦点一定位于双曲线的实轴上. ( )
(2)若两条双曲线的焦点相同,则其渐近线也一定相同. ( )
(3)焦点在x轴上的双曲线的离心率越大,其渐近线斜率的绝对值就越大. ( )
(4)焦点在x轴上的双曲线与焦点在y轴上的双曲线不可能具有共同的渐近线. ( )
(5)等轴双曲线的离心率等于 . ( )
答案:(1)√ (2)× (3)√ (4)× (5)√探究一探究二探究三思维辨析根据双曲线的标准方程研究其几何性质
【例1】 若点 是双曲线my2-4x2+4m=0上的一点,试求该双曲线的实轴长、虚轴长、焦距、焦点坐标、顶点坐标、渐近线方程、离心率.
思路点拨:先根据题意求出m的值,然后将双曲线方程化为标准方程,再写出其各个几何性质.探究一探究二探究三思维辨析反思感悟1.已知双曲线的方程研究其几何性质时,若不是标准方程,应先化为标准方程,确定方程中a,b的值,利用c2=a2+b2得到c,然后确定双曲线的焦点位置,从而写出双曲线的几何性质.
2.求双曲线的渐近线方程时,要特别注意焦点在x轴上还是在y轴上,以免写错.探究一探究二探究三思维辨析探究一探究二探究三思维辨析根据双曲线的几何性质求其标准方程
【例2】求解下列各题:思路点拨:对于(1)和(2),可直接设出双曲线方程,根据条件求出参数a,b的值,即得方程;对于(3)和(4),焦点位置不确定,应分类讨论,也可直接利用共渐近线的双曲线方程之间的关系求解.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟求双曲线标准方程的两种方法
1.根据双曲线的几何性质求其标准方程时,常用的方法是先定型(确定焦点在哪个轴上),后计算(确定a2,b2的值),要特别注意c2=a2+b2的应用,不要与椭圆中的关系混淆.
2.求双曲线标准方程,主要采用待定系数法,常用以下方法巧设双曲线方程进行求解:探究一探究二探究三思维辨析(5)渐近线为y=kx的双曲线的方程可设为k2x2-y2=λ(λ≠0);
(6)渐近线为ax±by=0的双曲线的方程可设为a2x2-b2y2=λ(λ≠0).探究一探究二探究三思维辨析探究一探究二探究三思维辨析双曲线的离心率与渐近线问题 探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析忽视双曲线的焦点位置致误 探究一探究二探究三思维辨析纠错心得:一般情况下,若只给出双曲线的渐近线方程、焦距、离心率等条件,要注意焦点位置的讨论,谨防丢解.探究一探究二探究三思维辨析跟踪训练已知双曲线的渐近线方程为5x±4y=0,实轴长为8,求双曲线的标准方程.
答案:(-∞,-4]∪[4,+∞) (-∞,+∞)【做一做3】 双曲线4x2-2y2=1的离心率等于 .?思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)双曲线的焦点一定位于双曲线的实轴上. ( )
(2)若两条双曲线的焦点相同,则其渐近线也一定相同. ( )
(3)焦点在x轴上的双曲线的离心率越大,其渐近线斜率的绝对值就越大. ( )
(4)焦点在x轴上的双曲线与焦点在y轴上的双曲线不可能具有共同的渐近线. ( )
(5)等轴双曲线的离心率等于 . ( )
答案:(1)√ (2)× (3)√ (4)× (5)√探究一探究二探究三思维辨析根据双曲线的标准方程研究其几何性质
【例1】 若点 是双曲线my2-4x2+4m=0上的一点,试求该双曲线的实轴长、虚轴长、焦距、焦点坐标、顶点坐标、渐近线方程、离心率.
思路点拨:先根据题意求出m的值,然后将双曲线方程化为标准方程,再写出其各个几何性质.探究一探究二探究三思维辨析反思感悟1.已知双曲线的方程研究其几何性质时,若不是标准方程,应先化为标准方程,确定方程中a,b的值,利用c2=a2+b2得到c,然后确定双曲线的焦点位置,从而写出双曲线的几何性质.
2.求双曲线的渐近线方程时,要特别注意焦点在x轴上还是在y轴上,以免写错.探究一探究二探究三思维辨析探究一探究二探究三思维辨析根据双曲线的几何性质求其标准方程
【例2】求解下列各题:思路点拨:对于(1)和(2),可直接设出双曲线方程,根据条件求出参数a,b的值,即得方程;对于(3)和(4),焦点位置不确定,应分类讨论,也可直接利用共渐近线的双曲线方程之间的关系求解.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟求双曲线标准方程的两种方法
1.根据双曲线的几何性质求其标准方程时,常用的方法是先定型(确定焦点在哪个轴上),后计算(确定a2,b2的值),要特别注意c2=a2+b2的应用,不要与椭圆中的关系混淆.
2.求双曲线标准方程,主要采用待定系数法,常用以下方法巧设双曲线方程进行求解:探究一探究二探究三思维辨析(5)渐近线为y=kx的双曲线的方程可设为k2x2-y2=λ(λ≠0);
(6)渐近线为ax±by=0的双曲线的方程可设为a2x2-b2y2=λ(λ≠0).探究一探究二探究三思维辨析探究一探究二探究三思维辨析双曲线的离心率与渐近线问题 探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析忽视双曲线的焦点位置致误 探究一探究二探究三思维辨析纠错心得:一般情况下,若只给出双曲线的渐近线方程、焦距、离心率等条件,要注意焦点位置的讨论,谨防丢解.探究一探究二探究三思维辨析跟踪训练已知双曲线的渐近线方程为5x±4y=0,实轴长为8,求双曲线的标准方程.
