2019-2020学年高中数学新人教A版选修1-1课件:第二章圆锥曲线与方程2.3.2抛物线的简单几何性质(22张PPT)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修1-1课件:第二章圆锥曲线与方程2.3.2抛物线的简单几何性质(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 765.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 08:50:14 | ||
图片预览








文档简介
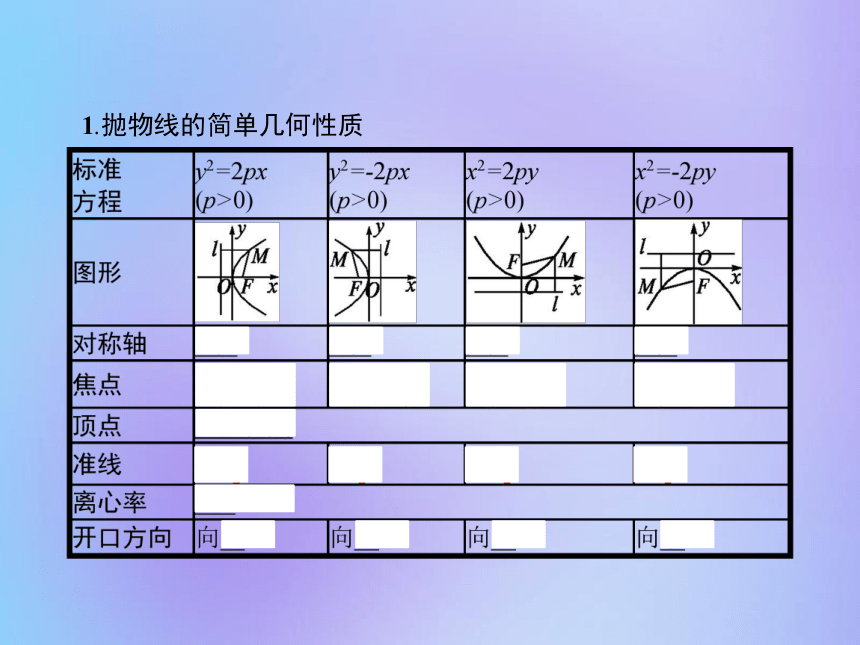
课件22张PPT。2.3.2 抛物线的简单几何性质1.抛物线的简单几何性质 名师点拨1.抛物线的几何性质与椭圆、双曲线相比有较大差别,它的离心率为定值1,只有一个焦点,一个顶点、一条对称轴、一条准线,没有渐近线,没有对称中心,通常称抛物线为无心圆锥曲线,而称椭圆、双曲线为有心圆锥曲线.
2.抛物线的焦点始终在对称轴上,抛物线的顶点就是抛物线与对称轴的交点,抛物线的准线始终与对称轴垂直,抛物线准线与对称轴的交点和焦点关于抛物线的顶点对称.
3.抛物线的通径:【做一做1】 (1)若点(m,n)在抛物线y2=-13x上,那么下列点中一定在该抛物线上的是( )
A.(-m,-n) B.(m,-n)
C.(-m,n) D.(-n,-m)
(2)顶点在原点,对称轴为y轴且过(4,1)的抛物线的准线与对称轴的交点坐标是 .?
解析:(1)由抛物线关于x轴对称易得.
(2)依题意设抛物线方程为x2=2py(p>0),则有42=2p·1,2p=16,于是抛物线方程为x2=16y,其准线为y=-4,准线与对称轴的交点坐标是(0,-4).
答案:(1)B (2)(0,-4)2.直线与抛物线的位置关系
设直线l:y=kx+b,抛物线C:y2=2px(p>0),将直线方程与抛物线方程联立消元得:k2x2+(2kb-2p)x+b2=0.则有:特别提醒直线与抛物线相交时,直线与抛物线不一定有两个公共点;直线与抛物线只有一个公共点时,直线与抛物线不一定相切,也有可能是相交,这时直线与抛物线的对称轴平行或重合.【做一做2】 (1)直线y=2x-1与抛物线 的位置关系是( )
A.相切 B.相交
C.相离 D.不确定
(2)过点(1,1)与抛物线y2=x只有一个公共点的直线有( )
A.1条 B.2条
C.3条 D.4条
解析:(1)
因为Δ=-1<0,所以直线与抛物线相离.
(2)因为点(1,1)在抛物线y2=x上,所以与y2=x只有一个公共点的直线有两条,其中一条为切线,一条为平行于x轴的直线.
答案:(1)C (2)B思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)在抛物线y2=2px(p>0)中,p值越大,抛物线的开口越开阔,p值越小,开口越扁狭. ( )
(2)抛物线既是轴对称图形也是中心对称图形. ( )
(3)抛物线的顶点一定在过焦点且与准线垂直的直线上. ( )
(4)直线与抛物线只有一个公共点,则直线与抛物线相切. ( )
(5)直线与抛物线相交时,直线与抛物线不一定有两个公共点. ( )
答案:(1)√ (2)× (3)√ (4)× (5)√探究一探究二探究三抛物线几何性质的应用
【例1】 抛物线y2=4x的焦点为F,准线为l,点A是抛物线上一点,且∠AFO=120°(O为坐标原点),AK⊥l,垂足为K,则△AKF的面积是 .?
思路点拨:要求△AKF的面积,只需求出点A的坐标即可.
自主解答:如图,设A(x0,y0),过A作AH⊥x轴于H,
在Rt△AFH中,|FH|=x0-1.
由∠AFO=120°得∠AFH=60°,探究一探究二探究三反思感悟利用抛物线的几何性质解决问题时,要熟练掌握各种形式的抛物线方程与其几何性质之间的对应关系,能够熟练地写出其焦点坐标与准线方程.探究一探究二探究三变式训练1若点A(6,4)在抛物线x2=-2py(p>0)的准线上,则点A与抛物线焦点F之间的距离等于 .?
解析:因为点A(6,4)在抛物线x2=-2py(p>0)的准线上,所以准线方程为y=4,于是焦点为F(0,-4),因此|AF|=
答案:10探究一探究二探究三直线与抛物线的位置关系及应用
【例2】 已知抛物线C:y2=2px(p>0)经过点A(1,-2).
(1)求抛物线方程,并求其准线方程;
(2)若直线l与OA平行,与抛物线有公共点,且直线OA与l的距离为
,求直线l的方程.
思路点拨:(1)将A点坐标代入抛物线方程即得p的值,从而得抛物线方程与准线方程;(2)设出直线l的方程与抛物线方程联立进行求解.探究一探究二探究三自主解答:(1)将点A(1,-2)代入抛物线y2=2px(p>0),
得(-2)2=2p×1,得p=2.
即抛物线C的方程为y2=4x,其准线方程为x=-1.
(2)设直线l的方程为y=-2x+t.反思感悟解决直线与抛物线位置关系的判断问题时,主要利用代数方法,即将直线方程与抛物线方程联立,通过方程组解的个数情况判断位置关系.探究一探究二探究三变式训练2过点(-3,2)的直线与抛物线y2=4x只有一个公共点,求此直线方程.探究一探究二探究三抛物线在实际问题中的应用
【例3】 如图所示,花坛水池中央有一喷泉,水管O'P=1 m,水从喷头P喷出后呈抛物线状,先向上至最高点后落下,若最高点距水面2 m,点P距抛物线的对称轴1 m,则水池的直径至少应设计多少米?(精确到1 m)
思路点拨:可以以抛物线的顶点为原点,对称轴为y轴建立平面直角坐标系,则易得点P坐标,再由P在抛物线上求出抛物线方程,设抛物线与水面的交点为B,则由点B的纵坐标求出点B的横坐标即可得解.探究一探究二探究三探究一探究二探究三反思感悟1.一般解决实际问题的步骤:
(1)建立适当的数学模型,将实际问题转换成数学问题;
(2)通过所学的数学知识进行求解.
2.利用抛物线模型解决实际问题时的关键点:
(1)一般将抛物线的顶点作为原点,将对称轴作为x轴或y轴建立坐标系,得到抛物线的标准方程;
(2)注意抛物线上关键点(焦点、顶点)的坐标;
(3)善于运用抛物线的对称性进行求解.探究一探究二探究三变式训练3一辆卡车高3 m,宽1.6 m,欲通过断面为抛物线型的隧道,已知拱口宽恰好是拱高的4倍,若拱口宽为a m,求使卡车通过的a的最小整数值.解析:由于通径长等于4,所以2p=4.
又因为经过点(2,1),所以方程只能为x2=4y.
答案:C解析:依题意,准线方程为x=2,于是 ,因此焦点坐标为(-2,0),故|MF|=5.
答案:B4.如图是抛物线形拱桥,当水面到直线l时,拱顶离水面2 m,水面宽为4 m.水位下降1 m后,水面宽为 m.?
2.抛物线的焦点始终在对称轴上,抛物线的顶点就是抛物线与对称轴的交点,抛物线的准线始终与对称轴垂直,抛物线准线与对称轴的交点和焦点关于抛物线的顶点对称.
3.抛物线的通径:【做一做1】 (1)若点(m,n)在抛物线y2=-13x上,那么下列点中一定在该抛物线上的是( )
A.(-m,-n) B.(m,-n)
C.(-m,n) D.(-n,-m)
(2)顶点在原点,对称轴为y轴且过(4,1)的抛物线的准线与对称轴的交点坐标是 .?
解析:(1)由抛物线关于x轴对称易得.
(2)依题意设抛物线方程为x2=2py(p>0),则有42=2p·1,2p=16,于是抛物线方程为x2=16y,其准线为y=-4,准线与对称轴的交点坐标是(0,-4).
答案:(1)B (2)(0,-4)2.直线与抛物线的位置关系
设直线l:y=kx+b,抛物线C:y2=2px(p>0),将直线方程与抛物线方程联立消元得:k2x2+(2kb-2p)x+b2=0.则有:特别提醒直线与抛物线相交时,直线与抛物线不一定有两个公共点;直线与抛物线只有一个公共点时,直线与抛物线不一定相切,也有可能是相交,这时直线与抛物线的对称轴平行或重合.【做一做2】 (1)直线y=2x-1与抛物线 的位置关系是( )
A.相切 B.相交
C.相离 D.不确定
(2)过点(1,1)与抛物线y2=x只有一个公共点的直线有( )
A.1条 B.2条
C.3条 D.4条
解析:(1)
因为Δ=-1<0,所以直线与抛物线相离.
(2)因为点(1,1)在抛物线y2=x上,所以与y2=x只有一个公共点的直线有两条,其中一条为切线,一条为平行于x轴的直线.
答案:(1)C (2)B思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)在抛物线y2=2px(p>0)中,p值越大,抛物线的开口越开阔,p值越小,开口越扁狭. ( )
(2)抛物线既是轴对称图形也是中心对称图形. ( )
(3)抛物线的顶点一定在过焦点且与准线垂直的直线上. ( )
(4)直线与抛物线只有一个公共点,则直线与抛物线相切. ( )
(5)直线与抛物线相交时,直线与抛物线不一定有两个公共点. ( )
答案:(1)√ (2)× (3)√ (4)× (5)√探究一探究二探究三抛物线几何性质的应用
【例1】 抛物线y2=4x的焦点为F,准线为l,点A是抛物线上一点,且∠AFO=120°(O为坐标原点),AK⊥l,垂足为K,则△AKF的面积是 .?
思路点拨:要求△AKF的面积,只需求出点A的坐标即可.
自主解答:如图,设A(x0,y0),过A作AH⊥x轴于H,
在Rt△AFH中,|FH|=x0-1.
由∠AFO=120°得∠AFH=60°,探究一探究二探究三反思感悟利用抛物线的几何性质解决问题时,要熟练掌握各种形式的抛物线方程与其几何性质之间的对应关系,能够熟练地写出其焦点坐标与准线方程.探究一探究二探究三变式训练1若点A(6,4)在抛物线x2=-2py(p>0)的准线上,则点A与抛物线焦点F之间的距离等于 .?
解析:因为点A(6,4)在抛物线x2=-2py(p>0)的准线上,所以准线方程为y=4,于是焦点为F(0,-4),因此|AF|=
答案:10探究一探究二探究三直线与抛物线的位置关系及应用
【例2】 已知抛物线C:y2=2px(p>0)经过点A(1,-2).
(1)求抛物线方程,并求其准线方程;
(2)若直线l与OA平行,与抛物线有公共点,且直线OA与l的距离为
,求直线l的方程.
思路点拨:(1)将A点坐标代入抛物线方程即得p的值,从而得抛物线方程与准线方程;(2)设出直线l的方程与抛物线方程联立进行求解.探究一探究二探究三自主解答:(1)将点A(1,-2)代入抛物线y2=2px(p>0),
得(-2)2=2p×1,得p=2.
即抛物线C的方程为y2=4x,其准线方程为x=-1.
(2)设直线l的方程为y=-2x+t.反思感悟解决直线与抛物线位置关系的判断问题时,主要利用代数方法,即将直线方程与抛物线方程联立,通过方程组解的个数情况判断位置关系.探究一探究二探究三变式训练2过点(-3,2)的直线与抛物线y2=4x只有一个公共点,求此直线方程.探究一探究二探究三抛物线在实际问题中的应用
【例3】 如图所示,花坛水池中央有一喷泉,水管O'P=1 m,水从喷头P喷出后呈抛物线状,先向上至最高点后落下,若最高点距水面2 m,点P距抛物线的对称轴1 m,则水池的直径至少应设计多少米?(精确到1 m)
思路点拨:可以以抛物线的顶点为原点,对称轴为y轴建立平面直角坐标系,则易得点P坐标,再由P在抛物线上求出抛物线方程,设抛物线与水面的交点为B,则由点B的纵坐标求出点B的横坐标即可得解.探究一探究二探究三探究一探究二探究三反思感悟1.一般解决实际问题的步骤:
(1)建立适当的数学模型,将实际问题转换成数学问题;
(2)通过所学的数学知识进行求解.
2.利用抛物线模型解决实际问题时的关键点:
(1)一般将抛物线的顶点作为原点,将对称轴作为x轴或y轴建立坐标系,得到抛物线的标准方程;
(2)注意抛物线上关键点(焦点、顶点)的坐标;
(3)善于运用抛物线的对称性进行求解.探究一探究二探究三变式训练3一辆卡车高3 m,宽1.6 m,欲通过断面为抛物线型的隧道,已知拱口宽恰好是拱高的4倍,若拱口宽为a m,求使卡车通过的a的最小整数值.解析:由于通径长等于4,所以2p=4.
又因为经过点(2,1),所以方程只能为x2=4y.
答案:C解析:依题意,准线方程为x=2,于是 ,因此焦点坐标为(-2,0),故|MF|=5.
答案:B4.如图是抛物线形拱桥,当水面到直线l时,拱顶离水面2 m,水面宽为4 m.水位下降1 m后,水面宽为 m.?
