2019-2020学年高中数学新人教A版选修1-1课件:第三章导数及其应用3.4生活中的优化问题举例(28张PPT)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修1-1课件:第三章导数及其应用3.4生活中的优化问题举例(28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 593.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 09:03:57 | ||
图片预览








文档简介
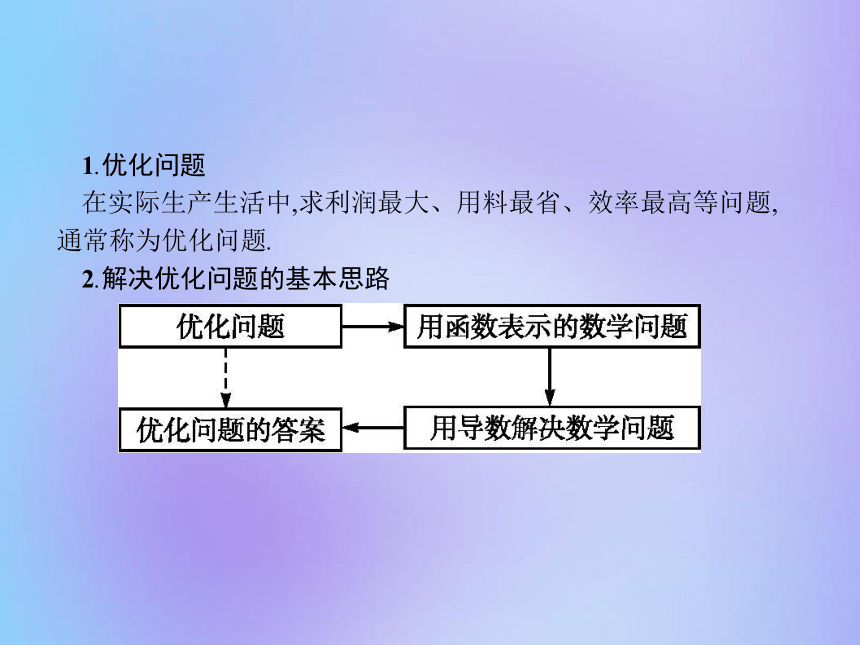
课件28张PPT。3.4 生活中的优化问题举例1.优化问题
在实际生产生活中,求利润最大、用料最省、效率最高等问题,通常称为优化问题.
2.解决优化问题的基本思路名师点拨解决实际优化问题的一般步骤
(1)认真阅读理解关于实际问题的材料,一般地,实际问题的材料都非常多,信息量较大,涉及的量也比较多,因此需要认真地、细心地阅读题目,发现其中有用的信息,揭示其数学本质.
(2)在理解题意的基础上,建立数学模型,把要解决的实际问题转化为数学问题,建立相应的函数关系式.
(3)针对数学模型,设计解决方案,用导数解决函数问题,同时要注意实际问题中变量的取值范围,即函数的定义域.
(4)根据数学问题的答案去回答实际问题中的优化问题.【做一做】 有矩形铁板,其长为6,宽为4,现从四个角上剪掉边长为x的四个小正方形,将剩余部分折成一个无盖的长方体盒子,要使容积最大,则x= .?思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)生活中的实际优化问题必须利用导数解决. ( )
(2)在解决实际优化问题时,若函数只有一个极值点,则极值点就是最值点. ( )
(3)求解实际优化问题时,必须考虑变量的实际意义,从而确定其取值范围. ( )
答案:(1)× (2)√ (3)√探究一探究二探究三思维辨析利润(收益)最大问题 思路点拨:由于投入的成本与x的不同取值范围有关,所以应该用分段函数表示利润函数,然后利用导数分段求解,求得最大值.探究一探究二探究三思维辨析L(x)在(80,100]上单调递增,∴L(x)max=L(100)=1 000ln 100-2 000.
∵1 000ln 50-250-(1 000ln 100-2 000)
=1 750-1 000ln 2>1 750-1 000>0,
∴当x=50,即年产量为50 000吨时,利润最大,最大利润为(1 000ln 50-250)万元.探究一探究二探究三思维辨析反思感悟利用导数解决利润(收益)最大问题,关键是灵活运用题设条件,建立利润(收益)的函数解析式,然后再利用导数方法求出该函数的最大值,即可得到最大利润(收益).常见的基本等量关系如下:
(1)利润(收益)=收入-成本;
(2)利润(收益)=每件产品的利润(收益)×销售量.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析面积与体积最大(小)问题
【例2】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形高科技工业园区.已知AB⊥BC, OA∥BC,AB=BC=2OA=4 km,曲线段OC是以点O 为顶点且开口向右的抛物线的一段.如果要使矩形的相邻两边分别落在AB,BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大用地面积.(精确到0.1 km2)探究一探究二探究三思维辨析思路点拨:首先应建立平面直角坐标系,求出抛物线段的方程,然后设出曲线段CO上顶点P的坐标,将矩形面积用P点坐标表示,最后用导数求其最大值.
自主解答:以O为坐标原点,OA所在直线为y轴,以O点到BC的垂线为x轴建立直角坐标系(图略),设矩形落在曲线段OC上的一个顶点为P,抛物线方程为y2=2px(p>0).
把点C(4,2)代入y2=2px(p>0),得4=8p,得 ,
∴y2=x(0≤x≤4,0≤y≤2).令P(t2,t)(0≤t<2),
记工业园区的用地面积为S km2,
则S=(4-t2)(t+2)=-t3-2t2+4t+8,0≤t<2.
∴S'=-3t2-4t+4=-(t+2)(3t-2).探究一探究二探究三思维辨析反思感悟求面积与体积的最值问题是实际生产生活中的常见问题,解决这类问题的关键是熟练掌握相关的面积、体积公式,能够依据题意确定出自变量的取值范围,建立准确的函数关系式,然后利用导数的方法加以解决,必要时,可选择建立坐标系,通过点的坐标建立函数关系式或曲线方程,以便于问题的解决.探究一探究二探究三思维辨析变式训练2要做一个圆锥形的漏斗,其母线长为20 cm,要使其体积最大,则高为多少?探究一探究二探究三思维辨析费用(用料)最省问题
【例3】 现有一批货物由海上从A地运往B地,已知轮船的最大航行速度为35海里/时,A地到B地之间的航行距离约为500海里,每小时的运输成本由燃料费和其余费用组成,轮船每小时的燃料费与轮船速度的平方成正比(比例系数为0.6),其余费用为每小时960元.
(1)把全程运输成本y(元)表示为速度x(海里/时)的函数;
(2)为了使全程运输成本最小,轮船应以多大速度航行?
思路点拨:(1)写出函数解析式时要注意函数的定义域;(2)利用导数求最值,注意函数定义域的限制.探究一探究二探究三思维辨析反思感悟用料最省、造价最低类问题的求解思路是找到变量之间的关系,借助关系建立函数关系式,然后借助导数予以求解.解题过程中要注意函数定义域的限制.探究一探究二探究三思维辨析变式训练3为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系: (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.探究一探究二探究三思维辨析探究一探究二探究三思维辨析忽视实际问题中变量的取值范围致误
【典例】 某厂生产一种机器,其固定成本(即固定投入)为0.5万元.但每生产100台,需要增加可变成本(即另增加投入)0.25万元.市场对此产品的年需求量为500台,销售收入(单位:万元)函数为: R(x)= (0≤x≤5),其中x是产品售出的数量(单位:百台).
(1)把利润y表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
易错分析:本题常见错误是忽视对年产量x的讨论,由于市场对该产品的年需求量为500台,所以当年产量x大于500台时,利润与x的关系不同于当年产量x小于500台时,应使用分段函数表示,分段求解.探究一探究二探究三思维辨析纠错心得在利用导数解决实际优化问题时,要注意对问题中变量取值范围的分析,应结合实际意义确定变量的取值范围,在变量的可取值范围内解决最值问题.探究一探究二探究三思维辨析跟踪训练已知A,B两地相距200千米,一只船从A地逆水到B地,水速为8千米/时,船在静水中的速度为v千米/时(8A.105 B.110 C.115 D.120
解析:利润为S(x)=(x-30)(200-x)=-x2+230x-6 000,S'(x)=-2x+230,
由S'(x)=0,得x=115,这时利润达到最大.
答案:C1234解析:设圆柱的底面半径为r,高为h,体积为V,
则4r+2h=l,答案:A 12343.容积为256的方底无盖水箱,它的高为 时最省材料.?12341234
在实际生产生活中,求利润最大、用料最省、效率最高等问题,通常称为优化问题.
2.解决优化问题的基本思路名师点拨解决实际优化问题的一般步骤
(1)认真阅读理解关于实际问题的材料,一般地,实际问题的材料都非常多,信息量较大,涉及的量也比较多,因此需要认真地、细心地阅读题目,发现其中有用的信息,揭示其数学本质.
(2)在理解题意的基础上,建立数学模型,把要解决的实际问题转化为数学问题,建立相应的函数关系式.
(3)针对数学模型,设计解决方案,用导数解决函数问题,同时要注意实际问题中变量的取值范围,即函数的定义域.
(4)根据数学问题的答案去回答实际问题中的优化问题.【做一做】 有矩形铁板,其长为6,宽为4,现从四个角上剪掉边长为x的四个小正方形,将剩余部分折成一个无盖的长方体盒子,要使容积最大,则x= .?思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)生活中的实际优化问题必须利用导数解决. ( )
(2)在解决实际优化问题时,若函数只有一个极值点,则极值点就是最值点. ( )
(3)求解实际优化问题时,必须考虑变量的实际意义,从而确定其取值范围. ( )
答案:(1)× (2)√ (3)√探究一探究二探究三思维辨析利润(收益)最大问题 思路点拨:由于投入的成本与x的不同取值范围有关,所以应该用分段函数表示利润函数,然后利用导数分段求解,求得最大值.探究一探究二探究三思维辨析L(x)在(80,100]上单调递增,∴L(x)max=L(100)=1 000ln 100-2 000.
∵1 000ln 50-250-(1 000ln 100-2 000)
=1 750-1 000ln 2>1 750-1 000>0,
∴当x=50,即年产量为50 000吨时,利润最大,最大利润为(1 000ln 50-250)万元.探究一探究二探究三思维辨析反思感悟利用导数解决利润(收益)最大问题,关键是灵活运用题设条件,建立利润(收益)的函数解析式,然后再利用导数方法求出该函数的最大值,即可得到最大利润(收益).常见的基本等量关系如下:
(1)利润(收益)=收入-成本;
(2)利润(收益)=每件产品的利润(收益)×销售量.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析面积与体积最大(小)问题
【例2】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形高科技工业园区.已知AB⊥BC, OA∥BC,AB=BC=2OA=4 km,曲线段OC是以点O 为顶点且开口向右的抛物线的一段.如果要使矩形的相邻两边分别落在AB,BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大用地面积.(精确到0.1 km2)探究一探究二探究三思维辨析思路点拨:首先应建立平面直角坐标系,求出抛物线段的方程,然后设出曲线段CO上顶点P的坐标,将矩形面积用P点坐标表示,最后用导数求其最大值.
自主解答:以O为坐标原点,OA所在直线为y轴,以O点到BC的垂线为x轴建立直角坐标系(图略),设矩形落在曲线段OC上的一个顶点为P,抛物线方程为y2=2px(p>0).
把点C(4,2)代入y2=2px(p>0),得4=8p,得 ,
∴y2=x(0≤x≤4,0≤y≤2).令P(t2,t)(0≤t<2),
记工业园区的用地面积为S km2,
则S=(4-t2)(t+2)=-t3-2t2+4t+8,0≤t<2.
∴S'=-3t2-4t+4=-(t+2)(3t-2).探究一探究二探究三思维辨析反思感悟求面积与体积的最值问题是实际生产生活中的常见问题,解决这类问题的关键是熟练掌握相关的面积、体积公式,能够依据题意确定出自变量的取值范围,建立准确的函数关系式,然后利用导数的方法加以解决,必要时,可选择建立坐标系,通过点的坐标建立函数关系式或曲线方程,以便于问题的解决.探究一探究二探究三思维辨析变式训练2要做一个圆锥形的漏斗,其母线长为20 cm,要使其体积最大,则高为多少?探究一探究二探究三思维辨析费用(用料)最省问题
【例3】 现有一批货物由海上从A地运往B地,已知轮船的最大航行速度为35海里/时,A地到B地之间的航行距离约为500海里,每小时的运输成本由燃料费和其余费用组成,轮船每小时的燃料费与轮船速度的平方成正比(比例系数为0.6),其余费用为每小时960元.
(1)把全程运输成本y(元)表示为速度x(海里/时)的函数;
(2)为了使全程运输成本最小,轮船应以多大速度航行?
思路点拨:(1)写出函数解析式时要注意函数的定义域;(2)利用导数求最值,注意函数定义域的限制.探究一探究二探究三思维辨析反思感悟用料最省、造价最低类问题的求解思路是找到变量之间的关系,借助关系建立函数关系式,然后借助导数予以求解.解题过程中要注意函数定义域的限制.探究一探究二探究三思维辨析变式训练3为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系: (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.探究一探究二探究三思维辨析探究一探究二探究三思维辨析忽视实际问题中变量的取值范围致误
【典例】 某厂生产一种机器,其固定成本(即固定投入)为0.5万元.但每生产100台,需要增加可变成本(即另增加投入)0.25万元.市场对此产品的年需求量为500台,销售收入(单位:万元)函数为: R(x)= (0≤x≤5),其中x是产品售出的数量(单位:百台).
(1)把利润y表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
易错分析:本题常见错误是忽视对年产量x的讨论,由于市场对该产品的年需求量为500台,所以当年产量x大于500台时,利润与x的关系不同于当年产量x小于500台时,应使用分段函数表示,分段求解.探究一探究二探究三思维辨析纠错心得在利用导数解决实际优化问题时,要注意对问题中变量取值范围的分析,应结合实际意义确定变量的取值范围,在变量的可取值范围内解决最值问题.探究一探究二探究三思维辨析跟踪训练已知A,B两地相距200千米,一只船从A地逆水到B地,水速为8千米/时,船在静水中的速度为v千米/时(8
解析:利润为S(x)=(x-30)(200-x)=-x2+230x-6 000,S'(x)=-2x+230,
由S'(x)=0,得x=115,这时利润达到最大.
答案:C1234解析:设圆柱的底面半径为r,高为h,体积为V,
则4r+2h=l,答案:A 12343.容积为256的方底无盖水箱,它的高为 时最省材料.?12341234
