2019-2020学年高中数学新人教A版选修1-1课件:第一章常用逻辑用语1.1.2四种命题1.1.3四种命题间的相互关系(26张PPT)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修1-1课件:第一章常用逻辑用语1.1.2四种命题1.1.3四种命题间的相互关系(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 436.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 00:00:00 | ||
图片预览






文档简介
课件26张PPT。1.1.2 四种命题
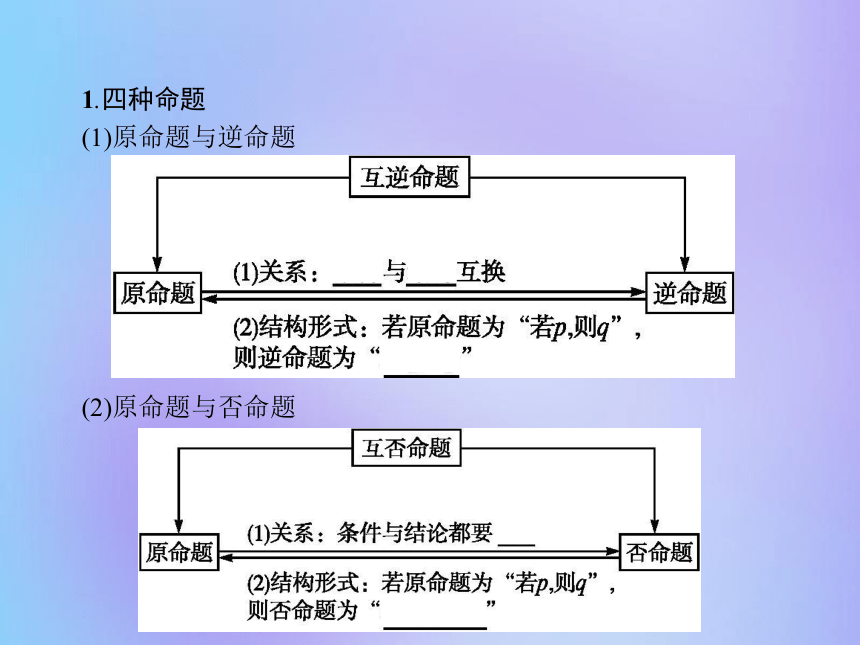
1.1.3 四种命题间的相互关系1.四种命题
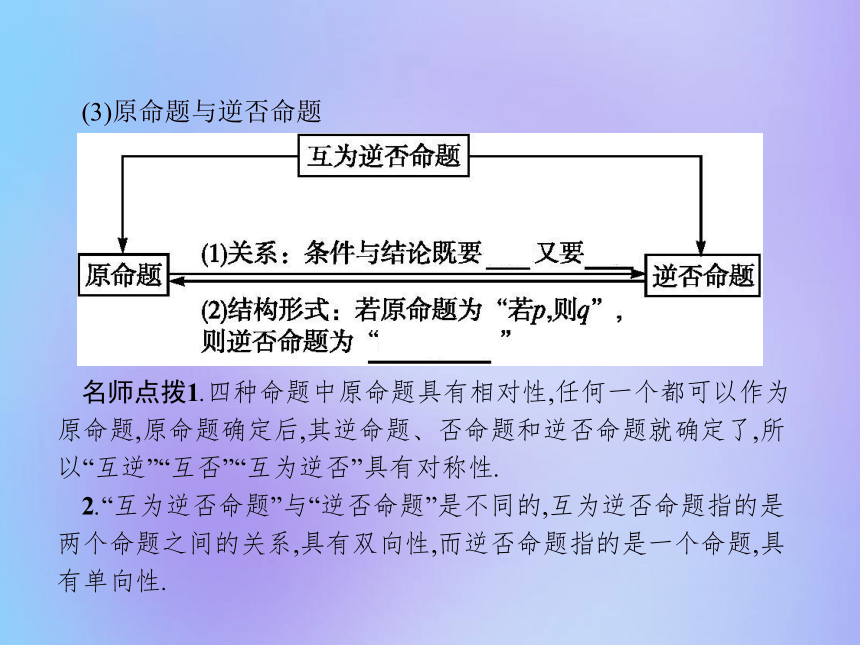
(1)原命题与逆命题(2)原命题与否命题 (3)原命题与逆否命题 名师点拨1.四种命题中原命题具有相对性,任何一个都可以作为原命题,原命题确定后,其逆命题、否命题和逆否命题就确定了,所以“互逆”“互否”“互为逆否”具有对称性.
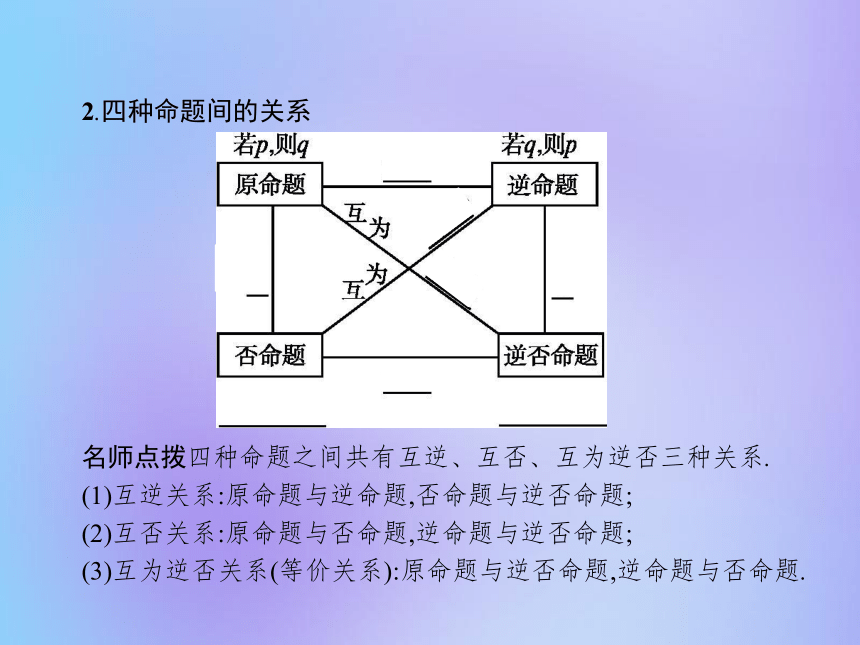
2.“互为逆否命题”与“逆否命题”是不同的,互为逆否命题指的是两个命题之间的关系,具有双向性,而逆否命题指的是一个命题,具有单向性.2.四种命题间的关系 名师点拨四种命题之间共有互逆、互否、互为逆否三种关系.
(1)互逆关系:原命题与逆命题,否命题与逆否命题;
(2)互否关系:原命题与否命题,逆命题与逆否命题;
(3)互为逆否关系(等价关系):原命题与逆否命题,逆命题与否命题.【做一做2】 给出以下命题:
①若一个四边形的四条边不相等,则它不是正方形;
②若一个四边形的对角互补,则它内接于圆;
③正方形的四条边相等;
④圆内接四边形的对角互补;
⑤对角不互补的四边形不内接于圆;
⑥若一个四边形的四条边相等,则它是正方形.
其中互为逆命题的有 ;互为否命题的有 ;互为逆否命题的有 .?
解析:命题③可改写为“若一个四边形是正方形,则它的四条边相等”;命题④可改写为“若一个四边形是圆内接四边形,则它的对角互补”;命题⑤可改写为“若一个四边形的对角不互补,则它不内接于圆”.因此互为逆命题的有③和⑥,②和④;互为否命题的有①和⑥,②和⑤;互为逆否命题的有①和③,④和⑤.
答案:③和⑥,②和④ ①和⑥,②和⑤ ①和③,④和⑤3.四种命题间的真假关系
(1)四种命题的真假性,有以下四种情况:(2)四种命题的真假性之间的关系如下:
①两个命题互为逆否命题,它们的真假性相同;
②两个命题互为逆命题或互为否命题,它们的真假性没有关系.
名师点拨由于原命题与其逆否命题的真假性相同,所以原命题与其逆否命题是等价命题,因此当直接证明原命题困难时,可以转化证明其逆否命题.【做一做3】 (1)命题“若x2≠1,则x≠1”的否命题是 (填“真”或“假”)命题.?
(2)若命题p的逆否命题是真命题,则命题p是 命题.(填“真”或“假”)?
(3)命题“若a>b,则a2>b2”的逆否命题为 ,其真假情况为 (填“真命题”或“假命题”).?
答案:(1)假 (2)真 (3)若a2≤b2,则a≤b 假命题思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)有的命题没有逆命题. ( )
(2)在四种命题中,只有原命题与否命题具有互否关系. ( )
(3)互逆命题的真假性一定相反. ( )
(4)在原命题及其逆命题、否命题和逆否命题中,假命题的个数一定是偶数. ( )
(5)原命题的否命题的逆命题就是原命题的逆否命题. ( )
答案:(1)× (2)× (3)× (4)√ (5)√探究一探究二思想方法写出原命题的其他三种命题
【例1】写出下列各个命题的逆命题、否命题和逆否命题.(2)若a+b是偶数,则a,b都是偶数;
(3)等底等高的两个三角形是全等三角形;
(4)当1(5)若ab=0,则a=0或b=0.
思路点拨:注意分清命题的条件和结论,然后按照四种命题的定义写出相应的命题,其中(2)要注意对“都是”的否定,(5)要注意对“或”的否定.探究一探究二思想方法(2)逆命题:若a,b都是偶数,
则a+b是偶数.
否命题:若a+b不是偶数,则a,b不都是偶数.
逆否命题:若a,b不都是偶数,
则a+b不是偶数.探究一探究二思想方法(3)逆命题:若两个三角形全等,则这两个三角形等底等高.
否命题:若两个三角形不等底或不等高,则这两个三角形不全等.
逆否命题:若两个三角形不全等,则这两个三角形不等底或不等高.
(4)逆命题:若x2-3x+2<0,则1否命题:若x≤1或x≥2,
则x2-3x+2≥0.
逆否命题:若x2-3x+2≥0,则x≤1或x≥2.
(5)逆命题:若a=0或b=0,则ab=0.
否命题:若ab≠0,则a≠0,且b≠0.
逆否命题:若a≠0,且b≠0,则ab≠0.探究一探究二思想方法反思感悟1.给出一个命题,写出该命题的其他三种形式时,首先要弄清楚该命题的条件和结论,若给出的命题不是“若p,则q”的形式,则应先改写为“若p,则q”的形式,找出命题的条件和结论.
2.写一个命题的否命题时,要对命题的条件和结论都进行否定,避免出现不否定条件,只否定结论的错误.
3.要特别注意一些常见形式的否定的写法,例如:“都是”的否定为“不都是”,“a,b中至少一个为零”的否定为“a,b都不为零”.探究一探究二思想方法变式训练1(1)若命题r的否命题为“若 p,则q”,那么原命题r为 .?
答案:若p,则 q
(2)写出命题“若抛物线y=ax2+bx+c(a≠0)的开口向下,则集合{x|ax2+bx+c<0,a≠0}≠?”的逆命题、否命题和逆否命题.
解:逆命题:若集合{x|ax2+bx+c<0,a≠0}≠?,
则抛物线y=ax2+bx+c(a≠0)的开口向下.
否命题:若抛物线y=ax2+bx+c(a≠0)的开口向上,
则集合{x|ax2+bx+c<0,a≠0}=?.
逆否命题:若集合{x|ax2+bx+c<0,a≠0)}=?,
则抛物线y=ax2+bx+c(a≠0)的开口向上.探究一探究二思想方法四种命题的真假判断
【例2】判断下列各个命题的真假:
(1)“若x+y=0,则x,y互为相反数”的否命题;
(2)“对顶角相等”的逆命题;
(3)“直角三角形的两个锐角互为余角”的逆否命题;
(4)若a≥0或b≥0,则a+b≥0.
思路点拨:可以直接根据要求写出每个命题,然后判断真假,也可以不写出命题,而利用四种命题之间的等价性关系进行判断.探究一探究二思想方法自主解答:(1)法一:“若x+y=0,则x,y互为相反数”的否命题是“若x+y≠0,则x,y不互为相反数”,是真命题.
法二:“若x+y=0,则x,y互为相反数”的逆命题是“若x,y互为相反数,则x+y=0”,显然是真命题,而逆命题和否命题等价,因此“若x+y=0,则x,y互为相反数”的否命题是真命题.
(2)法一:“对顶角相等”的逆命题是“若两个角相等,则它们是对顶角”,是假命题.
法二:“对顶角相等”的否命题是“若两个角不是对顶角,则它们不相等”,显然是假命题,而逆命题和否命题等价,故“对顶角相等”的逆命题是假命题.探究一探究二思想方法(3)法一:“直角三角形的两个锐角互为余角”的逆否命题是“若一个三角形的两个锐角不互为余角,则这个三角形不是直角三角形”,是真命题.
法二:由于命题“直角三角形的两个锐角互为余角”是真命题,而原命题与逆否命题等价,所以“直角三角形的两个锐角互为余角”的逆否命题是真命题.
(4)法一:取a=4,b=-6,满足a≥0或b≥0,但这时a+b≥0不成立,故原命题是假命题.
法二:命题“若a≥0或b≥0,则a+b≥0”的逆否命题是“若a+b<0,则a<0,且b<0”,显然是假命题,而原命题与逆否命题等价,所以原命题是假命题.探究一探究二思想方法反思感悟判断一个命题的真假通常有以下两种方法:
(1)分清该命题的条件与结论,直接对该命题的真假进行判断;
(2)不直接写出命题,而是根据命题之间的关系进行判断,即原命题与其逆否命题等价、逆命题与否命题等价,特别是当命题本身不容易判断真假时,通常都是通过判断其逆否命题的真假来判断.探究一探究二思想方法变式训练2(1)命题“个位数字为5的整数能被5整除”是 (填“真”或“假”)命题,它的逆命题是 (填“真”或“假”)命题.?
(2)下列说法正确的是 .?
① “若实数x,y满足x2+y2=0,则x,y全为零”的否命题是假命题;
②“正多边形都相似”的逆命题是真命题;
③“若 是有理数,则x是无理数”的逆否命题是真命题.探究一探究二思想方法解析:(1)显然原命题为真命题;而当一个整数能被5整除时,其末尾数字不一定为5,也可以为0,故逆命题是假命题.
(2)由于“若实数x,y满足x2+y2=0,则x,y全为零”的逆命题为“若x,y全为零,则x2+y2=0”,是真命题,所以“若实数x,y满足x2+y2=0,则x,y全为零”的否命题也是真命题,故①错误;相似的多边形不一定是正多边形,因此“正多边形都相似”的逆命题是假命题,故②错误;由于“若
是有理数,则x是无理数”是真命题,则其逆否命题也是真命题,故③正确.
答案:(1)真 假 (2)③探究一探究二思想方法等价性命题与“正难则反” 思想的应用
【典例】 若实数m,n满足m+n>3,求证:m2+n2≠4.
【审题视角】 将要证明的问题看做一个命题,只需证明这个命题为真命题即可,而当证明这个命题本身的真假比较困难时,可以利用命题的等价性证明其逆否命题为真命题.
自主解答:构造命题:若m+n>3,则m2+n2≠4.
该命题的逆否命题是:若m2+n2=4,则m+n≤3,以下证明该逆否命题为真命题.探究一探究二思想方法方法点睛“正难则反”思想的处理原则
(1)当原命题的真假不易判断,而逆否命题较容易判断真假时,可通过判断其逆否命题的真假来判断原命题的真假.
(2)在证明某一个命题的真假性有困难时,可以证明它的逆否命题为真(假)命题,来间接地证明原命题为真(假)命题.探究一探究二思想方法跟踪训练求证:当a2+b2=c2时,a,b,c不可能都是奇数.
证明:构造命题:若a2+b2=c2,则a,b,c不可能都是奇数.
该命题的逆否命题是:若a,b,c都是奇数,则a2+b2≠c2.下面证明该逆否命题是真命题.
由于a,b,c都是奇数,则a2,b2,c2都是奇数,于是a2+b2必为偶数,而c2为奇数,所以a2+b2≠c2,故逆否命题为真命题,从而原命题也是真命题.1.命题“若a+b=6,则ab≤9”的否命题是( )
A.若a+b=6,则ab>9 B.若ab≥9,则a+b≠6
C.若a+b≠6,则ab>9 D.若a+b≠6,则ab≤9
答案:C
2.已知命题s的逆命题是:“若??p,则q”,则命题s的否命题是( )
A.若q,则p B.若??q,则p C.若??q,则??p D.若p,则??q
解析:由已知得原命题s是“若q,则??p”,则s的否命题是“若??q,则p”.
答案:B
3.在命题“若a=5,则a2=25”及其逆命题、否命题、逆否命题这四个命题中,是假命题的是( )
A.原命题、否命题 B.原命题、逆命题
C.原命题、逆否命题 D.逆命题、否命题
解析:因为原命题为真命题,逆命题为假命题,所以其逆否命题为真命题,否命题为假命题.
答案:D4.下列命题中,真命题的个数是( )
①“若x,y都是奇数,则x+y是偶数”的否命题;②“全等三角形是相似三角形”的逆命题;③“圆内接四边形的对角互补”的逆否命题.
A.3 B.2 C.1 D.0
解析:①②是假命题,③是真命题.
答案:C
5.求证:若x+y≤8,则x,y中至少有一个不大于4.
证明:构造命题:若x+y≤8,则x,y中至少有一个不大于4.
其逆否命题是:若x,y都大于4,则x+y>8.
当x>4,y>4时,由不等式的性质可得x+y>8.
即逆否命题为真,故原命题为真命题,即原结论成立.
(1)原命题与逆命题(2)原命题与否命题 (3)原命题与逆否命题 名师点拨1.四种命题中原命题具有相对性,任何一个都可以作为原命题,原命题确定后,其逆命题、否命题和逆否命题就确定了,所以“互逆”“互否”“互为逆否”具有对称性.
2.“互为逆否命题”与“逆否命题”是不同的,互为逆否命题指的是两个命题之间的关系,具有双向性,而逆否命题指的是一个命题,具有单向性.2.四种命题间的关系 名师点拨四种命题之间共有互逆、互否、互为逆否三种关系.
(1)互逆关系:原命题与逆命题,否命题与逆否命题;
(2)互否关系:原命题与否命题,逆命题与逆否命题;
(3)互为逆否关系(等价关系):原命题与逆否命题,逆命题与否命题.【做一做2】 给出以下命题:
①若一个四边形的四条边不相等,则它不是正方形;
②若一个四边形的对角互补,则它内接于圆;
③正方形的四条边相等;
④圆内接四边形的对角互补;
⑤对角不互补的四边形不内接于圆;
⑥若一个四边形的四条边相等,则它是正方形.
其中互为逆命题的有 ;互为否命题的有 ;互为逆否命题的有 .?
解析:命题③可改写为“若一个四边形是正方形,则它的四条边相等”;命题④可改写为“若一个四边形是圆内接四边形,则它的对角互补”;命题⑤可改写为“若一个四边形的对角不互补,则它不内接于圆”.因此互为逆命题的有③和⑥,②和④;互为否命题的有①和⑥,②和⑤;互为逆否命题的有①和③,④和⑤.
答案:③和⑥,②和④ ①和⑥,②和⑤ ①和③,④和⑤3.四种命题间的真假关系
(1)四种命题的真假性,有以下四种情况:(2)四种命题的真假性之间的关系如下:
①两个命题互为逆否命题,它们的真假性相同;
②两个命题互为逆命题或互为否命题,它们的真假性没有关系.
名师点拨由于原命题与其逆否命题的真假性相同,所以原命题与其逆否命题是等价命题,因此当直接证明原命题困难时,可以转化证明其逆否命题.【做一做3】 (1)命题“若x2≠1,则x≠1”的否命题是 (填“真”或“假”)命题.?
(2)若命题p的逆否命题是真命题,则命题p是 命题.(填“真”或“假”)?
(3)命题“若a>b,则a2>b2”的逆否命题为 ,其真假情况为 (填“真命题”或“假命题”).?
答案:(1)假 (2)真 (3)若a2≤b2,则a≤b 假命题思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)有的命题没有逆命题. ( )
(2)在四种命题中,只有原命题与否命题具有互否关系. ( )
(3)互逆命题的真假性一定相反. ( )
(4)在原命题及其逆命题、否命题和逆否命题中,假命题的个数一定是偶数. ( )
(5)原命题的否命题的逆命题就是原命题的逆否命题. ( )
答案:(1)× (2)× (3)× (4)√ (5)√探究一探究二思想方法写出原命题的其他三种命题
【例1】写出下列各个命题的逆命题、否命题和逆否命题.(2)若a+b是偶数,则a,b都是偶数;
(3)等底等高的两个三角形是全等三角形;
(4)当1
思路点拨:注意分清命题的条件和结论,然后按照四种命题的定义写出相应的命题,其中(2)要注意对“都是”的否定,(5)要注意对“或”的否定.探究一探究二思想方法(2)逆命题:若a,b都是偶数,
则a+b是偶数.
否命题:若a+b不是偶数,则a,b不都是偶数.
逆否命题:若a,b不都是偶数,
则a+b不是偶数.探究一探究二思想方法(3)逆命题:若两个三角形全等,则这两个三角形等底等高.
否命题:若两个三角形不等底或不等高,则这两个三角形不全等.
逆否命题:若两个三角形不全等,则这两个三角形不等底或不等高.
(4)逆命题:若x2-3x+2<0,则1
则x2-3x+2≥0.
逆否命题:若x2-3x+2≥0,则x≤1或x≥2.
(5)逆命题:若a=0或b=0,则ab=0.
否命题:若ab≠0,则a≠0,且b≠0.
逆否命题:若a≠0,且b≠0,则ab≠0.探究一探究二思想方法反思感悟1.给出一个命题,写出该命题的其他三种形式时,首先要弄清楚该命题的条件和结论,若给出的命题不是“若p,则q”的形式,则应先改写为“若p,则q”的形式,找出命题的条件和结论.
2.写一个命题的否命题时,要对命题的条件和结论都进行否定,避免出现不否定条件,只否定结论的错误.
3.要特别注意一些常见形式的否定的写法,例如:“都是”的否定为“不都是”,“a,b中至少一个为零”的否定为“a,b都不为零”.探究一探究二思想方法变式训练1(1)若命题r的否命题为“若 p,则q”,那么原命题r为 .?
答案:若p,则 q
(2)写出命题“若抛物线y=ax2+bx+c(a≠0)的开口向下,则集合{x|ax2+bx+c<0,a≠0}≠?”的逆命题、否命题和逆否命题.
解:逆命题:若集合{x|ax2+bx+c<0,a≠0}≠?,
则抛物线y=ax2+bx+c(a≠0)的开口向下.
否命题:若抛物线y=ax2+bx+c(a≠0)的开口向上,
则集合{x|ax2+bx+c<0,a≠0}=?.
逆否命题:若集合{x|ax2+bx+c<0,a≠0)}=?,
则抛物线y=ax2+bx+c(a≠0)的开口向上.探究一探究二思想方法四种命题的真假判断
【例2】判断下列各个命题的真假:
(1)“若x+y=0,则x,y互为相反数”的否命题;
(2)“对顶角相等”的逆命题;
(3)“直角三角形的两个锐角互为余角”的逆否命题;
(4)若a≥0或b≥0,则a+b≥0.
思路点拨:可以直接根据要求写出每个命题,然后判断真假,也可以不写出命题,而利用四种命题之间的等价性关系进行判断.探究一探究二思想方法自主解答:(1)法一:“若x+y=0,则x,y互为相反数”的否命题是“若x+y≠0,则x,y不互为相反数”,是真命题.
法二:“若x+y=0,则x,y互为相反数”的逆命题是“若x,y互为相反数,则x+y=0”,显然是真命题,而逆命题和否命题等价,因此“若x+y=0,则x,y互为相反数”的否命题是真命题.
(2)法一:“对顶角相等”的逆命题是“若两个角相等,则它们是对顶角”,是假命题.
法二:“对顶角相等”的否命题是“若两个角不是对顶角,则它们不相等”,显然是假命题,而逆命题和否命题等价,故“对顶角相等”的逆命题是假命题.探究一探究二思想方法(3)法一:“直角三角形的两个锐角互为余角”的逆否命题是“若一个三角形的两个锐角不互为余角,则这个三角形不是直角三角形”,是真命题.
法二:由于命题“直角三角形的两个锐角互为余角”是真命题,而原命题与逆否命题等价,所以“直角三角形的两个锐角互为余角”的逆否命题是真命题.
(4)法一:取a=4,b=-6,满足a≥0或b≥0,但这时a+b≥0不成立,故原命题是假命题.
法二:命题“若a≥0或b≥0,则a+b≥0”的逆否命题是“若a+b<0,则a<0,且b<0”,显然是假命题,而原命题与逆否命题等价,所以原命题是假命题.探究一探究二思想方法反思感悟判断一个命题的真假通常有以下两种方法:
(1)分清该命题的条件与结论,直接对该命题的真假进行判断;
(2)不直接写出命题,而是根据命题之间的关系进行判断,即原命题与其逆否命题等价、逆命题与否命题等价,特别是当命题本身不容易判断真假时,通常都是通过判断其逆否命题的真假来判断.探究一探究二思想方法变式训练2(1)命题“个位数字为5的整数能被5整除”是 (填“真”或“假”)命题,它的逆命题是 (填“真”或“假”)命题.?
(2)下列说法正确的是 .?
① “若实数x,y满足x2+y2=0,则x,y全为零”的否命题是假命题;
②“正多边形都相似”的逆命题是真命题;
③“若 是有理数,则x是无理数”的逆否命题是真命题.探究一探究二思想方法解析:(1)显然原命题为真命题;而当一个整数能被5整除时,其末尾数字不一定为5,也可以为0,故逆命题是假命题.
(2)由于“若实数x,y满足x2+y2=0,则x,y全为零”的逆命题为“若x,y全为零,则x2+y2=0”,是真命题,所以“若实数x,y满足x2+y2=0,则x,y全为零”的否命题也是真命题,故①错误;相似的多边形不一定是正多边形,因此“正多边形都相似”的逆命题是假命题,故②错误;由于“若
是有理数,则x是无理数”是真命题,则其逆否命题也是真命题,故③正确.
答案:(1)真 假 (2)③探究一探究二思想方法等价性命题与“正难则反” 思想的应用
【典例】 若实数m,n满足m+n>3,求证:m2+n2≠4.
【审题视角】 将要证明的问题看做一个命题,只需证明这个命题为真命题即可,而当证明这个命题本身的真假比较困难时,可以利用命题的等价性证明其逆否命题为真命题.
自主解答:构造命题:若m+n>3,则m2+n2≠4.
该命题的逆否命题是:若m2+n2=4,则m+n≤3,以下证明该逆否命题为真命题.探究一探究二思想方法方法点睛“正难则反”思想的处理原则
(1)当原命题的真假不易判断,而逆否命题较容易判断真假时,可通过判断其逆否命题的真假来判断原命题的真假.
(2)在证明某一个命题的真假性有困难时,可以证明它的逆否命题为真(假)命题,来间接地证明原命题为真(假)命题.探究一探究二思想方法跟踪训练求证:当a2+b2=c2时,a,b,c不可能都是奇数.
证明:构造命题:若a2+b2=c2,则a,b,c不可能都是奇数.
该命题的逆否命题是:若a,b,c都是奇数,则a2+b2≠c2.下面证明该逆否命题是真命题.
由于a,b,c都是奇数,则a2,b2,c2都是奇数,于是a2+b2必为偶数,而c2为奇数,所以a2+b2≠c2,故逆否命题为真命题,从而原命题也是真命题.1.命题“若a+b=6,则ab≤9”的否命题是( )
A.若a+b=6,则ab>9 B.若ab≥9,则a+b≠6
C.若a+b≠6,则ab>9 D.若a+b≠6,则ab≤9
答案:C
2.已知命题s的逆命题是:“若??p,则q”,则命题s的否命题是( )
A.若q,则p B.若??q,则p C.若??q,则??p D.若p,则??q
解析:由已知得原命题s是“若q,则??p”,则s的否命题是“若??q,则p”.
答案:B
3.在命题“若a=5,则a2=25”及其逆命题、否命题、逆否命题这四个命题中,是假命题的是( )
A.原命题、否命题 B.原命题、逆命题
C.原命题、逆否命题 D.逆命题、否命题
解析:因为原命题为真命题,逆命题为假命题,所以其逆否命题为真命题,否命题为假命题.
答案:D4.下列命题中,真命题的个数是( )
①“若x,y都是奇数,则x+y是偶数”的否命题;②“全等三角形是相似三角形”的逆命题;③“圆内接四边形的对角互补”的逆否命题.
A.3 B.2 C.1 D.0
解析:①②是假命题,③是真命题.
答案:C
5.求证:若x+y≤8,则x,y中至少有一个不大于4.
证明:构造命题:若x+y≤8,则x,y中至少有一个不大于4.
其逆否命题是:若x,y都大于4,则x+y>8.
当x>4,y>4时,由不等式的性质可得x+y>8.
即逆否命题为真,故原命题为真命题,即原结论成立.
