2019-2020学年高中数学新人教A版选修1-1课件:第一章常用逻辑用语习题课——充分条件与必要条件的综合问题(21张PPT)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修1-1课件:第一章常用逻辑用语习题课——充分条件与必要条件的综合问题(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 599.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 00:00:00 | ||
图片预览








文档简介
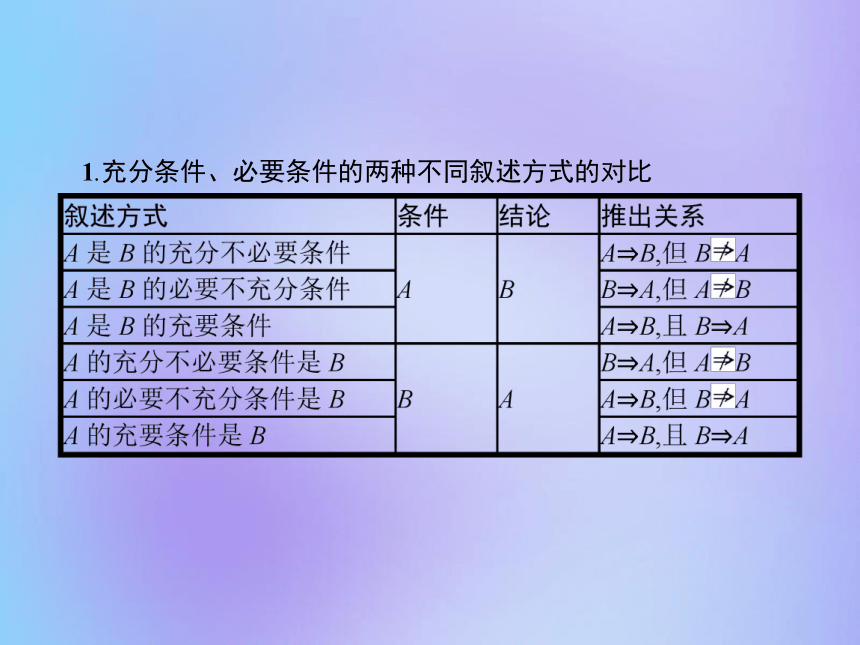
课件21张PPT。习题课——充分条件与必要条件的综合问题1.充分条件、必要条件的两种不同叙述方式的对比2.用集合之间的关系判断充分条件与必要条件的方法
若p,q中所涉及的问题与变量有关,p,q中相应变量的取值集合分别记为A,B,那么有以下结论:【做一做1】 设m∈R,则“m<4”的一个充分不必要条件是( )
A.m>4 B.m<2 C.m<6 D.m≤4
解析:由m<2可推得m<4,反之不成立,故m<4的一个充分不必要条件是m<2.
答案:B
【做一做2】 已知向量a=(x-1,2),b=(2,1),则a⊥b的充要条件是( )
A.x= B.x=-1 C.x=5 D.x=0
解析:因为a=(x-1,2),b=(2,1),a⊥b,
所以a·b=(x-1,2)·(2,1)=2(x-1)+2=2x=0,即x=0.
当x=0时,a=(-1,2),b=(2,1),a·b=-2+2=0,
∴a⊥b,故a⊥b的充要条件是x=0.
答案:D【做一做3】 若“x2+ax+2=0”是“x=1”的必要条件,则a= .
解析:由已知得x=1是方程x2+ax+2=0的根,所以12+a+2=0,所以a=-3.
答案:-3
【做一做4】 “x2<1”的充要条件是 .?
解析:解:不等式x2<1可得-1答案:-1【例1】 (1)一元二次方程ax2+bx+1=0(a≠0)有一个正根和一个负根的充分不必要条件是( )
A.a<0 B.a>0
C.a<-1 D.a<1
(2)一次函数 的图象同时经过第一、三、四象限的必要不充分条件是( )
A.m>1,n<-1 B.mn<0
C.m>0,n<0 D.m<0,n<0
(3)函数f(x)=x2+2x+4a没有零点的充要条件是 .?
思路点拨:(1)先寻找使结论成立的充要条件,然后将该充要条件缩小范围,即得相应的充分不必要条件;(2)先寻找使结论成立的充要条件,然后将该充要条件扩大范围,即得相应的必要不充分条件;(3)根据函数零点与方程根的关系直接探求充要条件.探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析反思感悟1.探求一个结论成立的充分不必要条件或必要不充分条件时,往往可以先找到其成立的充要条件,然后通过对充要条件的范围放大或缩小,得到相应的充分不必要条件或必要不充分条件.
2.如果p是q的充分不必要条件,那么p并不是唯一的,可以有多个;同样,如果p是q的必要不充分条件,那么p也不是唯一的,可以有多个;但如果p是q的充要条件,那么p是唯一的.探究一探究二思维辨析变式训练1(1)下列不等式:①x<1;②0-1.其中,可以作为x2<1的一个充分不必要条件的所有序号为 ;可以作为x2<1的一个必要不充分条件的所有序号为 .?
(2)直线x+y+m=0与圆(x-1)2+(y-1)2=2相切的充要条件是 .?
解析:(1)由x2<1解得-1-1},所以x<1和x>-1均可作为x2<1的一个必要不充分条件.
(2)直线x+y+m=0与圆(x-1)2+(y-1)2=2相切?圆心(1,1)到直线x+y+m=0的距离等于 或0.
答案:(1)②③ ①⑤ (2)m=-4或0探究一探究二思维辨析根据充分条件、必要条件求参数的取值范围 探究一探究二思维辨析反思感悟根据充分条件与必要条件求解参数取值范围的步骤如下:
(1)记集合M={x|p(x)},N={x|q(x)};
(2)根据以下表格确定集合M与N的包含关系:(3)根据集合M与N的包含关系建立关于参数的不等式(组);
(4)解不等式(组)求出参数的取值范围.探究一探究二思维辨析变式训练2(1)已知p:-4A.(-1,6)
B.[-1,6]
C.(-∞,-1)∪(6,+∞)
D.(-∞,-1]∪[6,+∞)
(2)若(x+2)(x-a)<0是0A.(-2,5] B.[-2,5]
C.[5,+∞) D.(5,+∞)探究一探究二思维辨析解析:(1)设q,p表示的范围分别为集合A,B,则A=(2,3),B=(a-4,a+4).
因为q是p的充分条件,则有A?B,即 所以-1≤a≤6.故选B.
(2)(x+2)(x-a)<0是0-2时,解(x+2)(x-a)<0得-2答案:(1)B (2)C探究一探究二思维辨析对问题的设问形式理解不清致误
【典例】 使不等式2x2-5x-3≥0成立的一个充分不必要条件是( )
A.x≥0 B.x>2或x<0
C.x∈{-1,3,5} D.x≥3或x≤
易错分析:本题常见的错解是对问题的设问方式理解不清,将条件和结论弄反,即将题意理解为:“2x2-5x-3≥0”是所选选项的充分不必要条件,从而出现错误结果.探究一探究二思维辨析探究一探究二思维辨析1.直线y=kx+1的倾斜角为钝角的一个必要不充分条件是( )
A.k<0 B.k<-1 C.k<1 D.k>-2
解析:直线y=kx+1的倾斜角为钝角的充要条件是斜率k<0,因此其必要不充分条件应该是k<1.
答案:C
2.“a+b>2c”的一个充分不必要条件是( )
A.a>c或b>c B.a>c或bC.a>c且bc且b>c
解析:由a>c且b>c可推出a+b>2c,但当a+b>2c时,推不出a>c且b>c,故选D.
答案:D4.若“x2-x<0”是“x>a”的充分不必要条件,则实数a的取值范围是 .?
解析:由x2-x<0可得0a”的充分不必要条件,所以a≤0.
答案:(-∞,0]
若p,q中所涉及的问题与变量有关,p,q中相应变量的取值集合分别记为A,B,那么有以下结论:【做一做1】 设m∈R,则“m<4”的一个充分不必要条件是( )
A.m>4 B.m<2 C.m<6 D.m≤4
解析:由m<2可推得m<4,反之不成立,故m<4的一个充分不必要条件是m<2.
答案:B
【做一做2】 已知向量a=(x-1,2),b=(2,1),则a⊥b的充要条件是( )
A.x= B.x=-1 C.x=5 D.x=0
解析:因为a=(x-1,2),b=(2,1),a⊥b,
所以a·b=(x-1,2)·(2,1)=2(x-1)+2=2x=0,即x=0.
当x=0时,a=(-1,2),b=(2,1),a·b=-2+2=0,
∴a⊥b,故a⊥b的充要条件是x=0.
答案:D【做一做3】 若“x2+ax+2=0”是“x=1”的必要条件,则a= .
解析:由已知得x=1是方程x2+ax+2=0的根,所以12+a+2=0,所以a=-3.
答案:-3
【做一做4】 “x2<1”的充要条件是 .?
解析:解:不等式x2<1可得-1
A.a<0 B.a>0
C.a<-1 D.a<1
(2)一次函数 的图象同时经过第一、三、四象限的必要不充分条件是( )
A.m>1,n<-1 B.mn<0
C.m>0,n<0 D.m<0,n<0
(3)函数f(x)=x2+2x+4a没有零点的充要条件是 .?
思路点拨:(1)先寻找使结论成立的充要条件,然后将该充要条件缩小范围,即得相应的充分不必要条件;(2)先寻找使结论成立的充要条件,然后将该充要条件扩大范围,即得相应的必要不充分条件;(3)根据函数零点与方程根的关系直接探求充要条件.探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析反思感悟1.探求一个结论成立的充分不必要条件或必要不充分条件时,往往可以先找到其成立的充要条件,然后通过对充要条件的范围放大或缩小,得到相应的充分不必要条件或必要不充分条件.
2.如果p是q的充分不必要条件,那么p并不是唯一的,可以有多个;同样,如果p是q的必要不充分条件,那么p也不是唯一的,可以有多个;但如果p是q的充要条件,那么p是唯一的.探究一探究二思维辨析变式训练1(1)下列不等式:①x<1;②0
(2)直线x+y+m=0与圆(x-1)2+(y-1)2=2相切的充要条件是 .?
解析:(1)由x2<1解得-1
(2)直线x+y+m=0与圆(x-1)2+(y-1)2=2相切?圆心(1,1)到直线x+y+m=0的距离等于 或0.
答案:(1)②③ ①⑤ (2)m=-4或0探究一探究二思维辨析根据充分条件、必要条件求参数的取值范围 探究一探究二思维辨析反思感悟根据充分条件与必要条件求解参数取值范围的步骤如下:
(1)记集合M={x|p(x)},N={x|q(x)};
(2)根据以下表格确定集合M与N的包含关系:(3)根据集合M与N的包含关系建立关于参数的不等式(组);
(4)解不等式(组)求出参数的取值范围.探究一探究二思维辨析变式训练2(1)已知p:-4
B.[-1,6]
C.(-∞,-1)∪(6,+∞)
D.(-∞,-1]∪[6,+∞)
(2)若(x+2)(x-a)<0是0
C.[5,+∞) D.(5,+∞)探究一探究二思维辨析解析:(1)设q,p表示的范围分别为集合A,B,则A=(2,3),B=(a-4,a+4).
因为q是p的充分条件,则有A?B,即 所以-1≤a≤6.故选B.
(2)(x+2)(x-a)<0是0
【典例】 使不等式2x2-5x-3≥0成立的一个充分不必要条件是( )
A.x≥0 B.x>2或x<0
C.x∈{-1,3,5} D.x≥3或x≤
易错分析:本题常见的错解是对问题的设问方式理解不清,将条件和结论弄反,即将题意理解为:“2x2-5x-3≥0”是所选选项的充分不必要条件,从而出现错误结果.探究一探究二思维辨析探究一探究二思维辨析1.直线y=kx+1的倾斜角为钝角的一个必要不充分条件是( )
A.k<0 B.k<-1 C.k<1 D.k>-2
解析:直线y=kx+1的倾斜角为钝角的充要条件是斜率k<0,因此其必要不充分条件应该是k<1.
答案:C
2.“a+b>2c”的一个充分不必要条件是( )
A.a>c或b>c B.a>c或b
解析:由a>c且b>c可推出a+b>2c,但当a+b>2c时,推不出a>c且b>c,故选D.
答案:D4.若“x2-x<0”是“x>a”的充分不必要条件,则实数a的取值范围是 .?
解析:由x2-x<0可得0
答案:(-∞,0]
