2018-2019学年天津市河西区八年级(下)期末数学试卷含解析
文档属性
| 名称 | 2018-2019学年天津市河西区八年级(下)期末数学试卷含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 98.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 11:59:24 | ||
图片预览



文档简介
2018-2019学年天津市河西区八年级(下)期末数学试卷
一、选择题:(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)注意事项每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点
1.(3分)化简的结果为( )
A.5 B.10 C.5 D.5
2.(3分)下列计算正确的是( )
A.+= B.2﹣= C.÷=3 D.×(﹣)=
3.(3分)在下列长度的各组线段中,能组成直角三角形的是( )
A.1,2,3 B.7,24,25 C.3,3,5 D.9,12,14
4.(3分)下列各点在直线y=2x+6上的是( )
A.(﹣5,4) B.(﹣7,20) C.(﹣5,﹣4) D.(7,﹣20)
5.(3分)如果某函数的图象如图所示,那么y随x的增大而( )
A.增大 B.减小
C.不变 D.有时增大有时减小
6.(3分)等边三角形的边长为2,则该等边三角形的面积是( )
A. B.2 C.1 D.
7.(3分)将直线y=3x+1向下平移2个单位长度,平移后直线的解析式为( )
A.y=3x﹣1 B.y=﹣3x+1 C.y=3x+3 D.y=x﹣3
8.(3分)下列方程中,没有实数根的是( )
A.x2+4=4x B.x2﹣x﹣1=0 C.2x2+4x+3=0 D.3x﹣8=0
9.(3分)要组织一次羽毛球邀请赛,参赛的两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排6天,每天安排6场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A.x(x+1)=36 B.x(x﹣1)=36
C.x(x+1)=36 D.x(x﹣1)=36
10.(3分)如图,有一正方形的纸片ABCD,边长为6,点E是DC边上一点且DC=3DE,把△ADE沿AE折叠使△ADE落在△AFE的位置,延长EF交BC边于点G,连接BF有以下四个结论:
①∠GAE=45°;
②BG+DE=GE;
③点G是BC的中点;
④连接FC,则BF⊥FC;
其中正确的结论序号是( )
A.①②③④ B.①②③ C.①② D.②③
二、填空题:(本大题共6小题,每小题3分,共18分.务必将答案涂写在“答题卡”上答案答在试卷上无效.)
11.(3分)方程x2=9的根是 .
12.(3分)在实数范围内,使得有意义的x的取值范围为 .
13.(3分)已知一次函数的图象经过点(0,2),且满足y随x的增大而增大,则该一次函数的解析式可以为 (写出一个即可)
14.(3分)一个直角三角形的两条直角边长分别为2,,则这个直角三角形的斜边长为 .
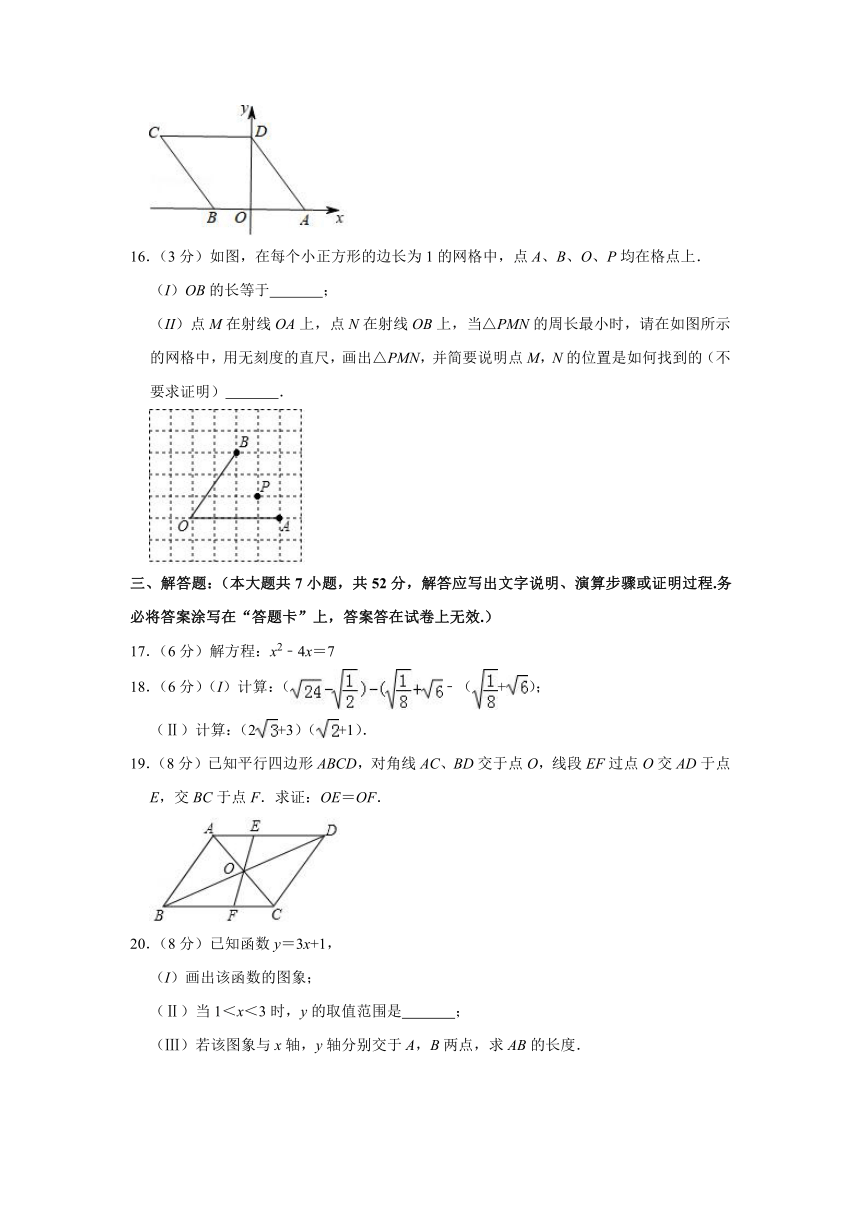
15.(3分)如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标是 .
16.(3分)如图,在每个小正方形的边长为1的网格中,点A、B、O、P均在格点上.
(I)OB的长等于 ;
(II)点M在射线OA上,点N在射线OB上,当△PMN的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出△PMN,并简要说明点M,N的位置是如何找到的(不要求证明) .
三、解答题:(本大题共7小题,共52分,解答应写出文字说明、演算步骤或证明过程.务必将答案涂写在“答题卡”上,答案答在试卷上无效.)
17.(6分)解方程:x2﹣4x=7
18.(6分)(I)计算:(﹣(+);
(Ⅱ)计算:(2+3)(+1).
19.(8分)已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF.
20.(8分)已知函数y=3x+1,
(I)画出该函数的图象;
(Ⅱ)当1<x<3时,y的取值范围是 ;
(Ⅲ)若该图象与x轴,y轴分别交于A,B两点,求AB的长度.
21.(8分)用配方法解一元二次方程x2+4x+c=0(c为常数)
22.(8分)用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
一次复印页数(页)
5
10
20
30
…
甲复印店收费(元)
0.5
2
…
乙复印店收费(元)
0.6
2.4
…
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.
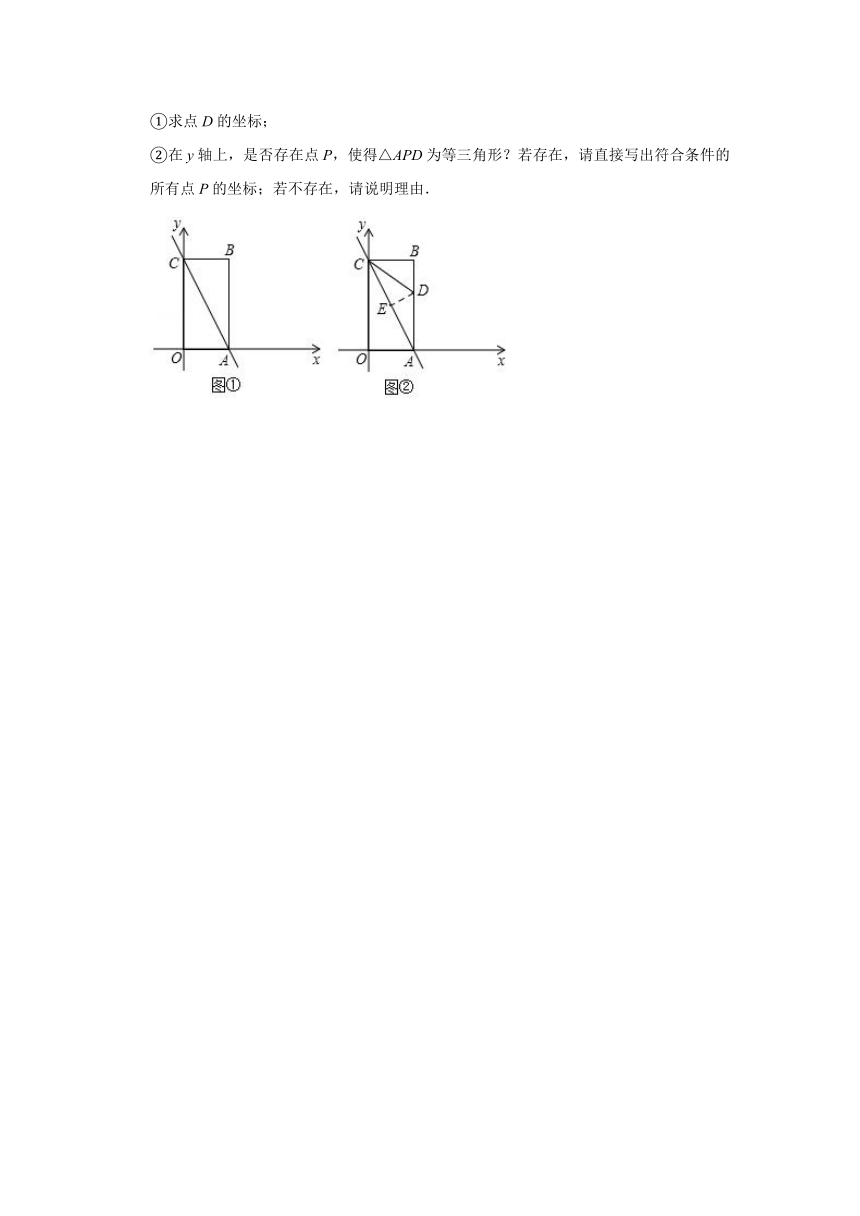
23.(8分)如图①,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.
(I)线段AB,BC,AC的长分别为:
AB= BC= AC= ;
(Ⅱ)折叠△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E连接CD,如图②
①求点D的坐标;
②在y轴上,是否存在点P,使得△APD为等三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
2018-2019学年天津市河西区八年级(下)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)注意事项每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点
1.【解答】解:=5,
故选:D.
2.【解答】解:A、+无法计算,故此选项错误;
B、2﹣=,故此选项正确;
C、÷=,故此选项错误;
D、×(﹣)=﹣,故此选项错误;
故选:B.
3.【解答】解:A、因为12+22≠32,所以不能组成直角三角形;
B、因为72+242=252,所以能组成直角三角形;
C、因为32+32≠52,所以不能组成直角三角形;
D、因为92+122≠142,所以不能组成直角三角形.
故选:B.
4.【解答】解:把x=﹣5代入y=2x+6得:y=﹣10+6=﹣4,
即当x=﹣5时,y=﹣4.过点(﹣5,﹣4)
故选:C.
5.【解答】解:由函数图象可得,
y随x的增大而增大,
故选:A.
6.【解答】解:AB=2,∵等边三角形高线即中点,
∴BD=CD=1,
在Rt△ABD中,AB=2,BD=1,
∴AD==,
∴等边△ABC的面积为BC?AD=×2×=,
故选:A.
7.【解答】解:将直线y=3x+1向下平移2个单位长度,平移后直线的解析式为y=3x+1﹣2,即y=3x﹣1.
故选:A.
8.【解答】解:A、x2+4=4x,△=(﹣4)2﹣4×1×4=0,方程有实数根,此选项不符合题意;
B、x2﹣x﹣1=0,△=(﹣1)2﹣4×1×(﹣1)=5>0,方程有实数根,此选项不符合题意;
C、2x2+4x+3=0,△=42﹣4×2×3=﹣8<0,方程没有实数根,此选项符合题意;
D、3x﹣8=0,x=,方程有实数根,此选项不符合题意;
故选:C.
9.【解答】解:由题意可得,x(x﹣1)=6×6,
即:x(x﹣1)=36,
故选:B.
10.【解答】解:连接AG,AG和BF交于H,如图所示:
∵正方形ABCD的边长为6,DC=3DE,
∴DE=2,EC=4,
∵把△ADE沿AE折叠使△ADE落在△AFE的位置,
∴AF=AD=AB=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,
在Rt△ABG和Rt△AFG中,,
∴Rt△ABG≌Rt△AFG(HL),
∴GB=GF,∠BAG=∠FAG,
∴∠GAE=∠FAE+∠FAG=∠BAD=45°,①正确;
∴GE=GF+EF=BG+DE,②正确;
设BG=x,则GF=x,CG=BC﹣BG=6﹣x,
在Rt△CGE中,GE=x+2,EC=4,CG=6﹣x,
∵CG2+CE2=GE2,
∴(6﹣x)2+42=(x+2)2,解得x=3,
∴BG=3,CG=6﹣3=3,
∴BG=CG,即点G为BC的中点,③正确;
∴GF=GC,
∴∠GFC=∠GCF,
又∵Rt△ABG≌Rt△AFG,
∴∠AGB=∠AGF,
而∠BGF=∠GFC+∠GCF,
∴∠AGB+∠AGF=∠GFC+∠GCF,
∴∠AGB=∠GCF,
∴FC∥AG,
∵AB=AF,BG=FG,
∴AG⊥BF,
∴BF⊥FC,④正确;
故选:A.
二、填空题:(本大题共6小题,每小题3分,共18分.务必将答案涂写在“答题卡”上答案答在试卷上无效.)
11.【解答】解:x2=9,
开方得:x1=3,x2=﹣3,
故答案为:x1=3,x2=﹣3.
12.【解答】解:在实数范围内,使得有意义
则3+x≥0,
解得:x≥﹣3.
故答案为:x≥﹣3.
13.【解答】解:∵一次函数y=kx+b的图象经过点(0,2),
∴b=2,
又∵y随x的增大而增大,
∴k>0 即可,
因此只要写出一个k>0,b=2的一个一次函数的关系式就可以.
故答案可以为:y=x+2
14.【解答】解:这个直角三角形的斜边长==,
故答案为:.
15.【解答】解:∵菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,
∴AB=5,
∴AD=5,
∴由勾股定理知:OD===4,
∴点C的坐标是:(﹣5,4).
故答案为:(﹣5,4).
16.【解答】解:(1)OB=,
(2)如图所示:
作点P关于OA,OB的对称点,连接两个对称点交OB于N,交OA于M即可;
故答案为:;作点P关于OA,OB的对称点,连接两个对称点交OB于N即可.
三、解答题:(本大题共7小题,共52分,解答应写出文字说明、演算步骤或证明过程.务必将答案涂写在“答题卡”上,答案答在试卷上无效.)
17.【解答】解:方程配方得:x2﹣4x+4=11,即(x﹣2)2=11,
开方得:x﹣2=±,
解得:x1=2+,x2=2﹣.
18.【解答】解:(Ⅰ)原式=2﹣﹣﹣
=﹣;
(Ⅱ)原式=2+2+3+3.
19.【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF.
20.【解答】解:(Ⅰ)∵函数y=3x+1,
∴当x=0时,y=1,当x=1时,y=4,
则该函数的图象一定过点(0,1)和点(1,4)两点,函数图象如右图所示;
(Ⅱ)函数y=3x+1,
∴当x=1时,y=4,当x=3时,y=10,该函数y随x的增大而增大,
故答案为:4<x<10;
(Ⅲ)∵函数y=3x+1,
∴当x=0时,y=1,当y=0时,x=﹣,
即点A(0,1),点B(﹣,0),
∴AB==
21.【解答】解:方程整理得:x2+4x=﹣c,
配方得:x2+4x+4=4﹣c,即(x+2)2=4﹣c,
当4﹣c>0时,x+2=±,即x1=﹣2+,x2=﹣2﹣;
当4﹣c=0时,x1=x2=﹣2;
当4﹣c<0时,方程无解.
22.【解答】解:(1)当x=10时,甲复印店收费为:0,1×10=1;乙复印店收费为:0.12×10=1.2;
当x=30时,甲复印店收费为:0,1×30=3;乙复印店收费为:0.12×20+0.09×10=3.3;
故答案为1,3;1.2,3.3;
(2)y1=0.1x(x≥0);
y2=;
(3)顾客在乙复印店复印花费少;
当x>70时,y1=0.1x,y2=0.09x+0.6,
设y=y1﹣y2,
∴y1﹣y2=0.1x﹣(0.09x+0.6)=0.01x﹣0.6,
设y=0.01x﹣0.6,
由0.01>0,则y随x的增大而增大,
当x=70时,y=0.1
∴x>70时,y>0.1,
∴y1>y2,
∴当x>70时,顾客在乙复印店复印花费少.
23.【解答】解:(Ⅰ)∵一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,
∴A(4,0),C(0,8),
∴OA=4,OC=8,
∵AB⊥x轴,CB⊥y轴,∠AOC=90°,
∴四边形OABC是矩形,
∴AB=OC=8,BC=OA=4,
在Rt△ABC中,根据勾股定理得,AC==4,
故答案为:8,4,4;
(Ⅱ)A、①由(1)知,BC=4,AB=8,
由折叠知,CD=AD,
在Rt△BCD中,BD=AB﹣AD=8﹣AD,
根据勾股定理得,CD2=BC2+BD2,
即:AD2=16+(8﹣AD)2,
∴AD=5,
∴D(4,5).
②由①知,D(4,5),
设P(0,y),
∵A(4,0),
∴AP2=16+y2,DP2=16+(y﹣5)2,
∵△APD为等腰三角形,
∴Ⅰ、AP=AD,
∴16+y2=25,
∴y=±3,
∴P(0,3)或(0,﹣3)
Ⅱ、AP=DP,
∴16+y2=16+(y﹣5)2,
∴y=,
∴P(0,),
Ⅲ、AD=DP,25=16+(y﹣5)2,
∴y=2或8,
∴P(0,2)或(0,8).
综上所述,满足条件的点P坐标为(0,3)或(0,﹣3)或(0,)或(0,2)或(0,8).
一、选择题:(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)注意事项每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点
1.(3分)化简的结果为( )
A.5 B.10 C.5 D.5
2.(3分)下列计算正确的是( )
A.+= B.2﹣= C.÷=3 D.×(﹣)=
3.(3分)在下列长度的各组线段中,能组成直角三角形的是( )
A.1,2,3 B.7,24,25 C.3,3,5 D.9,12,14
4.(3分)下列各点在直线y=2x+6上的是( )
A.(﹣5,4) B.(﹣7,20) C.(﹣5,﹣4) D.(7,﹣20)
5.(3分)如果某函数的图象如图所示,那么y随x的增大而( )
A.增大 B.减小
C.不变 D.有时增大有时减小
6.(3分)等边三角形的边长为2,则该等边三角形的面积是( )
A. B.2 C.1 D.
7.(3分)将直线y=3x+1向下平移2个单位长度,平移后直线的解析式为( )
A.y=3x﹣1 B.y=﹣3x+1 C.y=3x+3 D.y=x﹣3
8.(3分)下列方程中,没有实数根的是( )
A.x2+4=4x B.x2﹣x﹣1=0 C.2x2+4x+3=0 D.3x﹣8=0
9.(3分)要组织一次羽毛球邀请赛,参赛的两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排6天,每天安排6场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A.x(x+1)=36 B.x(x﹣1)=36
C.x(x+1)=36 D.x(x﹣1)=36
10.(3分)如图,有一正方形的纸片ABCD,边长为6,点E是DC边上一点且DC=3DE,把△ADE沿AE折叠使△ADE落在△AFE的位置,延长EF交BC边于点G,连接BF有以下四个结论:
①∠GAE=45°;
②BG+DE=GE;
③点G是BC的中点;
④连接FC,则BF⊥FC;
其中正确的结论序号是( )
A.①②③④ B.①②③ C.①② D.②③
二、填空题:(本大题共6小题,每小题3分,共18分.务必将答案涂写在“答题卡”上答案答在试卷上无效.)
11.(3分)方程x2=9的根是 .
12.(3分)在实数范围内,使得有意义的x的取值范围为 .
13.(3分)已知一次函数的图象经过点(0,2),且满足y随x的增大而增大,则该一次函数的解析式可以为 (写出一个即可)
14.(3分)一个直角三角形的两条直角边长分别为2,,则这个直角三角形的斜边长为 .
15.(3分)如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标是 .
16.(3分)如图,在每个小正方形的边长为1的网格中,点A、B、O、P均在格点上.
(I)OB的长等于 ;
(II)点M在射线OA上,点N在射线OB上,当△PMN的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出△PMN,并简要说明点M,N的位置是如何找到的(不要求证明) .
三、解答题:(本大题共7小题,共52分,解答应写出文字说明、演算步骤或证明过程.务必将答案涂写在“答题卡”上,答案答在试卷上无效.)
17.(6分)解方程:x2﹣4x=7
18.(6分)(I)计算:(﹣(+);
(Ⅱ)计算:(2+3)(+1).
19.(8分)已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF.
20.(8分)已知函数y=3x+1,
(I)画出该函数的图象;
(Ⅱ)当1<x<3时,y的取值范围是 ;
(Ⅲ)若该图象与x轴,y轴分别交于A,B两点,求AB的长度.
21.(8分)用配方法解一元二次方程x2+4x+c=0(c为常数)
22.(8分)用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
一次复印页数(页)
5
10
20
30
…
甲复印店收费(元)
0.5
2
…
乙复印店收费(元)
0.6
2.4
…
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.
23.(8分)如图①,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.
(I)线段AB,BC,AC的长分别为:
AB= BC= AC= ;
(Ⅱ)折叠△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E连接CD,如图②
①求点D的坐标;
②在y轴上,是否存在点P,使得△APD为等三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
2018-2019学年天津市河西区八年级(下)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)注意事项每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点
1.【解答】解:=5,
故选:D.
2.【解答】解:A、+无法计算,故此选项错误;
B、2﹣=,故此选项正确;
C、÷=,故此选项错误;
D、×(﹣)=﹣,故此选项错误;
故选:B.
3.【解答】解:A、因为12+22≠32,所以不能组成直角三角形;
B、因为72+242=252,所以能组成直角三角形;
C、因为32+32≠52,所以不能组成直角三角形;
D、因为92+122≠142,所以不能组成直角三角形.
故选:B.
4.【解答】解:把x=﹣5代入y=2x+6得:y=﹣10+6=﹣4,
即当x=﹣5时,y=﹣4.过点(﹣5,﹣4)
故选:C.
5.【解答】解:由函数图象可得,
y随x的增大而增大,
故选:A.
6.【解答】解:AB=2,∵等边三角形高线即中点,
∴BD=CD=1,
在Rt△ABD中,AB=2,BD=1,
∴AD==,
∴等边△ABC的面积为BC?AD=×2×=,
故选:A.
7.【解答】解:将直线y=3x+1向下平移2个单位长度,平移后直线的解析式为y=3x+1﹣2,即y=3x﹣1.
故选:A.
8.【解答】解:A、x2+4=4x,△=(﹣4)2﹣4×1×4=0,方程有实数根,此选项不符合题意;
B、x2﹣x﹣1=0,△=(﹣1)2﹣4×1×(﹣1)=5>0,方程有实数根,此选项不符合题意;
C、2x2+4x+3=0,△=42﹣4×2×3=﹣8<0,方程没有实数根,此选项符合题意;
D、3x﹣8=0,x=,方程有实数根,此选项不符合题意;
故选:C.
9.【解答】解:由题意可得,x(x﹣1)=6×6,
即:x(x﹣1)=36,
故选:B.
10.【解答】解:连接AG,AG和BF交于H,如图所示:
∵正方形ABCD的边长为6,DC=3DE,
∴DE=2,EC=4,
∵把△ADE沿AE折叠使△ADE落在△AFE的位置,
∴AF=AD=AB=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,
在Rt△ABG和Rt△AFG中,,
∴Rt△ABG≌Rt△AFG(HL),
∴GB=GF,∠BAG=∠FAG,
∴∠GAE=∠FAE+∠FAG=∠BAD=45°,①正确;
∴GE=GF+EF=BG+DE,②正确;
设BG=x,则GF=x,CG=BC﹣BG=6﹣x,
在Rt△CGE中,GE=x+2,EC=4,CG=6﹣x,
∵CG2+CE2=GE2,
∴(6﹣x)2+42=(x+2)2,解得x=3,
∴BG=3,CG=6﹣3=3,
∴BG=CG,即点G为BC的中点,③正确;
∴GF=GC,
∴∠GFC=∠GCF,
又∵Rt△ABG≌Rt△AFG,
∴∠AGB=∠AGF,
而∠BGF=∠GFC+∠GCF,
∴∠AGB+∠AGF=∠GFC+∠GCF,
∴∠AGB=∠GCF,
∴FC∥AG,
∵AB=AF,BG=FG,
∴AG⊥BF,
∴BF⊥FC,④正确;
故选:A.
二、填空题:(本大题共6小题,每小题3分,共18分.务必将答案涂写在“答题卡”上答案答在试卷上无效.)
11.【解答】解:x2=9,
开方得:x1=3,x2=﹣3,
故答案为:x1=3,x2=﹣3.
12.【解答】解:在实数范围内,使得有意义
则3+x≥0,
解得:x≥﹣3.
故答案为:x≥﹣3.
13.【解答】解:∵一次函数y=kx+b的图象经过点(0,2),
∴b=2,
又∵y随x的增大而增大,
∴k>0 即可,
因此只要写出一个k>0,b=2的一个一次函数的关系式就可以.
故答案可以为:y=x+2
14.【解答】解:这个直角三角形的斜边长==,
故答案为:.
15.【解答】解:∵菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,
∴AB=5,
∴AD=5,
∴由勾股定理知:OD===4,
∴点C的坐标是:(﹣5,4).
故答案为:(﹣5,4).
16.【解答】解:(1)OB=,
(2)如图所示:
作点P关于OA,OB的对称点,连接两个对称点交OB于N,交OA于M即可;
故答案为:;作点P关于OA,OB的对称点,连接两个对称点交OB于N即可.
三、解答题:(本大题共7小题,共52分,解答应写出文字说明、演算步骤或证明过程.务必将答案涂写在“答题卡”上,答案答在试卷上无效.)
17.【解答】解:方程配方得:x2﹣4x+4=11,即(x﹣2)2=11,
开方得:x﹣2=±,
解得:x1=2+,x2=2﹣.
18.【解答】解:(Ⅰ)原式=2﹣﹣﹣
=﹣;
(Ⅱ)原式=2+2+3+3.
19.【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF.
20.【解答】解:(Ⅰ)∵函数y=3x+1,
∴当x=0时,y=1,当x=1时,y=4,
则该函数的图象一定过点(0,1)和点(1,4)两点,函数图象如右图所示;
(Ⅱ)函数y=3x+1,
∴当x=1时,y=4,当x=3时,y=10,该函数y随x的增大而增大,
故答案为:4<x<10;
(Ⅲ)∵函数y=3x+1,
∴当x=0时,y=1,当y=0时,x=﹣,
即点A(0,1),点B(﹣,0),
∴AB==
21.【解答】解:方程整理得:x2+4x=﹣c,
配方得:x2+4x+4=4﹣c,即(x+2)2=4﹣c,
当4﹣c>0时,x+2=±,即x1=﹣2+,x2=﹣2﹣;
当4﹣c=0时,x1=x2=﹣2;
当4﹣c<0时,方程无解.
22.【解答】解:(1)当x=10时,甲复印店收费为:0,1×10=1;乙复印店收费为:0.12×10=1.2;
当x=30时,甲复印店收费为:0,1×30=3;乙复印店收费为:0.12×20+0.09×10=3.3;
故答案为1,3;1.2,3.3;
(2)y1=0.1x(x≥0);
y2=;
(3)顾客在乙复印店复印花费少;
当x>70时,y1=0.1x,y2=0.09x+0.6,
设y=y1﹣y2,
∴y1﹣y2=0.1x﹣(0.09x+0.6)=0.01x﹣0.6,
设y=0.01x﹣0.6,
由0.01>0,则y随x的增大而增大,
当x=70时,y=0.1
∴x>70时,y>0.1,
∴y1>y2,
∴当x>70时,顾客在乙复印店复印花费少.
23.【解答】解:(Ⅰ)∵一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,
∴A(4,0),C(0,8),
∴OA=4,OC=8,
∵AB⊥x轴,CB⊥y轴,∠AOC=90°,
∴四边形OABC是矩形,
∴AB=OC=8,BC=OA=4,
在Rt△ABC中,根据勾股定理得,AC==4,
故答案为:8,4,4;
(Ⅱ)A、①由(1)知,BC=4,AB=8,
由折叠知,CD=AD,
在Rt△BCD中,BD=AB﹣AD=8﹣AD,
根据勾股定理得,CD2=BC2+BD2,
即:AD2=16+(8﹣AD)2,
∴AD=5,
∴D(4,5).
②由①知,D(4,5),
设P(0,y),
∵A(4,0),
∴AP2=16+y2,DP2=16+(y﹣5)2,
∵△APD为等腰三角形,
∴Ⅰ、AP=AD,
∴16+y2=25,
∴y=±3,
∴P(0,3)或(0,﹣3)
Ⅱ、AP=DP,
∴16+y2=16+(y﹣5)2,
∴y=,
∴P(0,),
Ⅲ、AD=DP,25=16+(y﹣5)2,
∴y=2或8,
∴P(0,2)或(0,8).
综上所述,满足条件的点P坐标为(0,3)或(0,﹣3)或(0,)或(0,2)或(0,8).
同课章节目录
