2018-2019学年上海市嘉定区八年级(上)期末数学试卷含解析(沪教版五四制)
文档属性
| 名称 | 2018-2019学年上海市嘉定区八年级(上)期末数学试卷含解析(沪教版五四制) |

|
|
| 格式 | zip | ||
| 文件大小 | 115.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 00:00:00 | ||
图片预览




文档简介
2018-2019学年上海市嘉定区八年级(上)期末数学试卷
一、选择题(本大题共有6题,每小题3分,满分18分)
1.(3分)下列各式中与是同类二次根式的是( )
A. B. C. D.
2.(3分)下列方程中,属于一元二次方程的是( )
A. B.2y+x2=1 C.x2﹣2=0 D.=4
3.(3分)下列关于x的二次三项式中(m表示实数),在实数范围内一定能分解因式的是( )
A.x2﹣2x+2 B.2x2﹣mx+1 C.x2﹣2x+m D.x2﹣mx﹣1
4.(3分)正比例函数y=k1x(k1≠0)与反比例函数y=的大致图象如图所示,那么k1、k2的取值范围是( )
A.k1>0,k2> B.k1>0,k2< C.k1<0,k2> D.k1<0,k2<
5.(3分)下列四个命题:(1)三角形的一条中线把三角形分成面积相等的两部分;(2)有两边和其中一边的对角对应相等的两三角形全等;(3)点P(1,2)关于原点的对称点坐标为P′(﹣1,﹣2);(4)若=a,则a>0;其中真命题的有( )
A.(1)、(2) B.(1)、(3) C.(2)、(3) D.(3)、(4)
6.(3分)如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )
①DE=AC;②DE⊥AC;③∠EAF=∠ADE;④∠CAB=30°.
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共有12题,每小题2分,满分24分)
7.(2分)×= .
8.(2分)方程x2=4x的解是 .
9.(2分)不解方程,判断方程3x2+2x=﹣1的根的情况 .
10.(2分)某商场八月份的营业额是100万元,预计十月份的营业额可达到144万元,若九、十月份营业额的月增长率相同为x,那么由题意可列得方程为 .
11.(2分)已知关于x的方程x2+(m﹣2)x+m2﹣1=0有两个实数根,那么m的取值范围是 .
12.(2分)函数的定义域是 .
13.(2分)已知f(x)=,则f(﹣1)= .
14.(2分)命题“等腰三角形的两个底角相等”的逆命题是 .
15.(2分)经过已知点M和N的圆的圆心的轨迹是 .
16.(2分)如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=10cm,则AD= cm.
17.(2分)如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= .
18.(2分)在△ABC中,AB=5,AC=7,AD是BC边上的中线,则AD的取值范围是 .
三、解答题(本大题共7题,满分58分)
19.(7分)计算:.
20.(7分)解方程:3x(x﹣1)﹣2=2x.
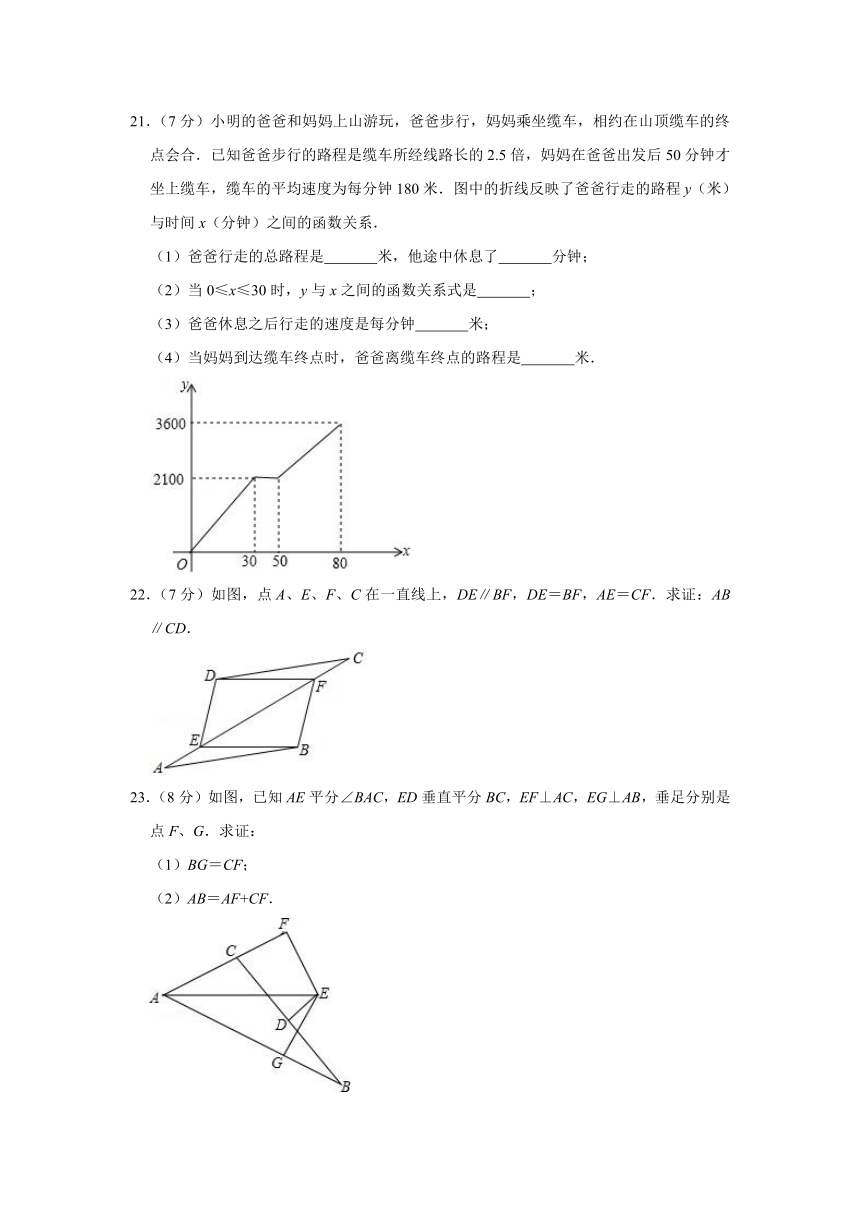
21.(7分)小明的爸爸和妈妈上山游玩,爸爸步行,妈妈乘坐缆车,相约在山顶缆车的终点会合.已知爸爸步行的路程是缆车所经线路长的2.5倍,妈妈在爸爸出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米.图中的折线反映了爸爸行走的路程y(米)与时间x(分钟)之间的函数关系.
(1)爸爸行走的总路程是 米,他途中休息了 分钟;
(2)当0≤x≤30时,y与x之间的函数关系式是 ;
(3)爸爸休息之后行走的速度是每分钟 米;
(4)当妈妈到达缆车终点时,爸爸离缆车终点的路程是 米.
22.(7分)如图,点A、E、F、C在一直线上,DE∥BF,DE=BF,AE=CF.求证:AB∥CD.
23.(8分)如图,已知AE平分∠BAC,ED垂直平分BC,EF⊥AC,EG⊥AB,垂足分别是点F、G.求证:
(1)BG=CF;
(2)AB=AF+CF.
24.(10分)已知反比例函数y=的图象与正比例函数y=k2x(k2≠0)的图象都经过点A(m,2),点P(﹣3,﹣4)在反比例函数y=的图象上,点B(﹣3,n)在正比例函数y=k2x(k2≠0)的图象上.
(1)求此正比例函数的解析式;
(2)求线段AB的长;
(3)求△PAB的面积.
25.(12分)如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,点P是AB边上一个动点,过点P作AB的垂线交AC边与点D,以PD为边作∠DPE=60°,PE交BC边与点E.
(1)当点D为AC边的中点时,求BE的长;
(2)当PD=PE时,求AP的长;
(3)设AP的长为x,四边形CDPE的面积为y,请直接写出y与x的函数解析式及自变量x的取值范围.
2018-2019学年上海市嘉定区八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共有6题,每小题3分,满分18分)
1.【解答】解:A.=3,与是同类二次根式;
B.=2,与不是同类二次根式;
C.=,与不是同类二次根式;
D.与不是同类二次根式;
故选:A.
2.【解答】解:x2﹣2=0为一元二次方程.
故选:C.
3.【解答】解:选项A,x2﹣2x+2=0,△=4﹣4×2=﹣4<0,方程没有实数根,即x2﹣2x+2在数范围内不能分解因式;
选项B,2x2﹣mx+1=0,△=m2﹣8的值有可能小于0,即2x2﹣mx+1在数范围内不一定能分解因式;
选项C,x2﹣2x+m=0,△=4﹣4m的值有可能小于0,即x2﹣2x+m在数范围内不一定能分解因式;
选项D,x2﹣mx﹣1=0,△=m2+4>0,方程有两个不相等的实数根,即x2﹣mx﹣1在数范围内一定能分解因式.
故选:D.
4.【解答】解:正比例函数y=k1x过一、三象限,故k1>0;
反比例函数y=的图象在二、四象限,故2k2﹣1<0,即k2<.
故选:B.
5.【解答】解:(1)三角形的一条中线能将三角形分成面积相等的两部分,正确;
(2)有两边和其中一边的对角对应相等的两个三角形全等,错误;
(3)点P(1,2)关于原点的对称点坐标为(﹣1,﹣2),正确;
(4)若=a,则a≥0,故本小题错误.
综上所述,正确的是(1)(3).
故选:B.
6.【解答】解:点D是AB的中点,则AD=,
∵AB=2BC,
∴AD=BC,
∵EA⊥AB,CB⊥AB,
∴∠B=∠EAB=90°,
在△AED与△BAC中,
,
∴△AED≌△BAC,
∴∠E=∠CAB,DE=AC,
∴①正确;
∵∠E+∠EDA=90°,
∴∠FAD+∠EDA=90°,
∴∠AFD=180°﹣(∠FAD+∠EDA)=90°,
∴DE⊥AC,
∴②正确;
∵∠EAF与∠ADE都是∠E的余角,
∴∠EAF=∠ADE,
∴③正确;
∵BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,
∴④错误;
故选:C.
二、填空题(本大题共有12题,每小题2分,满分24分)
7.【解答】解:×
=
=
=.
8.【解答】解:原方程可化为:x2﹣4x=0,
∴x(x﹣4)=0
解得x=0或4;
故方程的解为:0,4.
9.【解答】解:由3x2+2x=﹣1得到:3x2+2x+1=0.
∵a=3,b=2,c=1,
∴△=b2﹣4ac=8﹣12=﹣4<0,
∴一元二次方程3x2+2x=﹣1无实数根.
故答案为:无实数根.
10.【解答】解:设九、十月份营业额的月平均增长率为x,
依题意,得:100(1+x)2=144.
故答案为:100(1+x)2=144.
11.【解答】解:∵关于x的方程x2+(m﹣2)x+m2﹣1=0有两个实数根,
∴△=(m﹣2)2﹣4×1×(m2﹣1)=﹣4m+8≥0,
∴m≤2.
故答案为:m≤2.
12.【解答】解:根据题意得:3x﹣2≥0,
解得:x≥.
故答案是:x≥.
13.【解答】解:f(﹣1)==4,
故答案为:4.
14.【解答】解:因为原命题的题设是:“一个三角形是等腰三角形”,结论是“这个三角形两底角相等”,
所以命题“等腰三角形的两个底角相等”的逆命题是“两个角相等三角形是等腰三角形”.
15.【解答】解:根据同圆的半径相等,则圆心应满足到点M和点N的距离相等,即经过已知点M和点N的圆的圆心的轨迹是线段MN的垂直平分线.
故答案为:线段MN的垂直平分线.
16.【解答】解:∵DE是边AB的垂直平分线,
∴DE=CD=10cm,
∵DE⊥AB,∠A=30°,
∴AD=2DE=20cm,
故答案为:20.
17.【解答】解:在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,
∵∠ACB=60°,∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
故答案为∠CHD=45°.
18.【解答】解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
∵,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵AB=5,BE=AC=7,
∴7﹣5<2AD<7+5,即2<2x<12,
∴1<AD<6.
故答案为:1<AD<6.
三、解答题(本大题共7题,满分58分)
19.【解答】解:原式=2+3×﹣(+)
=2+﹣4
=﹣.
20.【解答】解:
3x(x﹣1)﹣2=2x
3x2﹣3x﹣2=2x
3x2﹣5x﹣2=0
(3x+1)(x﹣2)=0
解得:x1=,x2=2
21.【解答】故答案为:y=70x;
(3)爸爸休息之后行走的速度是(3600﹣2100)÷(80﹣50)=50米/分钟,
故答案为:50.
(4)妈妈到达缆车终点的时间为:(分),
爸爸迟到80﹣50﹣8=22(分),
终点时,爸爸离缆车终点的路程为:22×50=1100(米),
故答案为:1100.
22.【解答】证明:∵DE∥BF
∴∠DEF=∠BFE
∵AE=CF
∴AF=CE,且DE=BF,∠DEF=∠BFE
∴△AFB≌△CED(SAS)
∴∠A=∠C
∴AB∥CD
23.【解答】证明:(1)连接CE、BE,
∵ED垂直平分BC,
∴EC=EB,
∵AE平分∠CAB,EF⊥AC,EG⊥AB,
∴EF=EG,
在Rt△CFE和Rt△BGE中,
,
∴Rt△CFE≌Rt△BGE,
∴BG=CF;
(2)∵AE平分∠BAC,EF⊥AC,EG⊥AB,
∴EF=EG,
在Rt△AGE和Rt△AFE中,
,
∴Rt△AGE≌Rt△AFE,
∴AG=AF,
∵AB=AG+BG,
∴AB=AF+CF.
24.【解答】解:(1)∵点(﹣3,﹣4)在反比例函数y=图象上,
∴k1=﹣3×(﹣4)=12.
∵点A(m,2)在反比例函数y=图象上,
∴2m=12,
∴m=6,
∴点A的坐标为(6,2);
∵正比例函数y=k2x(k2≠0)的图象都经过点A(6,2),
∴2=6k2,解得k2,=,
∴正比例函数为y=x;
(2)∵点B(﹣3,n)在正比例函数y=x的图象上,
∴n=﹣3×=﹣1,
∴点B的坐标为(﹣3,﹣1),
∴AB==3.
(3)∵点B的坐标为(﹣3,﹣1),P(﹣3,﹣4),
∴BP=3,
又∵A(6,2),
∴△PAB的面积=BP×h=×3×9=.
25.【解答】解:(1)在△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=AB=2,
∴AC==2,
∵D是AC的中点,
∴AD=,DP=,AP=,
∴BP=AB﹣AP=,
∵∠DPE=60°,
∴∠EPB=30°,
∴EB=BP=;
(2)设AP=x,则BP=4﹣x,
在两个有30°的Rt△APD,Rt△BPE中,AD=2DP,BP=2BE,
由勾股定理解得PD=x,PE=(4﹣x),
因为PD=PE,
所以x=(4﹣x),
解得x=,即AP=;
(3)由(2)知:AP=x,PD=x,PE=(4﹣x),BE=(4﹣x),
∴y=S△ABC﹣S△APD﹣S△BPE
=×2×2﹣?x?x﹣×(4﹣x)?(4﹣x)
=﹣x2+x(0<x<3).
一、选择题(本大题共有6题,每小题3分,满分18分)
1.(3分)下列各式中与是同类二次根式的是( )
A. B. C. D.
2.(3分)下列方程中,属于一元二次方程的是( )
A. B.2y+x2=1 C.x2﹣2=0 D.=4
3.(3分)下列关于x的二次三项式中(m表示实数),在实数范围内一定能分解因式的是( )
A.x2﹣2x+2 B.2x2﹣mx+1 C.x2﹣2x+m D.x2﹣mx﹣1
4.(3分)正比例函数y=k1x(k1≠0)与反比例函数y=的大致图象如图所示,那么k1、k2的取值范围是( )
A.k1>0,k2> B.k1>0,k2< C.k1<0,k2> D.k1<0,k2<
5.(3分)下列四个命题:(1)三角形的一条中线把三角形分成面积相等的两部分;(2)有两边和其中一边的对角对应相等的两三角形全等;(3)点P(1,2)关于原点的对称点坐标为P′(﹣1,﹣2);(4)若=a,则a>0;其中真命题的有( )
A.(1)、(2) B.(1)、(3) C.(2)、(3) D.(3)、(4)
6.(3分)如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )
①DE=AC;②DE⊥AC;③∠EAF=∠ADE;④∠CAB=30°.
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共有12题,每小题2分,满分24分)
7.(2分)×= .
8.(2分)方程x2=4x的解是 .
9.(2分)不解方程,判断方程3x2+2x=﹣1的根的情况 .
10.(2分)某商场八月份的营业额是100万元,预计十月份的营业额可达到144万元,若九、十月份营业额的月增长率相同为x,那么由题意可列得方程为 .
11.(2分)已知关于x的方程x2+(m﹣2)x+m2﹣1=0有两个实数根,那么m的取值范围是 .
12.(2分)函数的定义域是 .
13.(2分)已知f(x)=,则f(﹣1)= .
14.(2分)命题“等腰三角形的两个底角相等”的逆命题是 .
15.(2分)经过已知点M和N的圆的圆心的轨迹是 .
16.(2分)如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=10cm,则AD= cm.
17.(2分)如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= .
18.(2分)在△ABC中,AB=5,AC=7,AD是BC边上的中线,则AD的取值范围是 .
三、解答题(本大题共7题,满分58分)
19.(7分)计算:.
20.(7分)解方程:3x(x﹣1)﹣2=2x.
21.(7分)小明的爸爸和妈妈上山游玩,爸爸步行,妈妈乘坐缆车,相约在山顶缆车的终点会合.已知爸爸步行的路程是缆车所经线路长的2.5倍,妈妈在爸爸出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米.图中的折线反映了爸爸行走的路程y(米)与时间x(分钟)之间的函数关系.
(1)爸爸行走的总路程是 米,他途中休息了 分钟;
(2)当0≤x≤30时,y与x之间的函数关系式是 ;
(3)爸爸休息之后行走的速度是每分钟 米;
(4)当妈妈到达缆车终点时,爸爸离缆车终点的路程是 米.
22.(7分)如图,点A、E、F、C在一直线上,DE∥BF,DE=BF,AE=CF.求证:AB∥CD.
23.(8分)如图,已知AE平分∠BAC,ED垂直平分BC,EF⊥AC,EG⊥AB,垂足分别是点F、G.求证:
(1)BG=CF;
(2)AB=AF+CF.
24.(10分)已知反比例函数y=的图象与正比例函数y=k2x(k2≠0)的图象都经过点A(m,2),点P(﹣3,﹣4)在反比例函数y=的图象上,点B(﹣3,n)在正比例函数y=k2x(k2≠0)的图象上.
(1)求此正比例函数的解析式;
(2)求线段AB的长;
(3)求△PAB的面积.
25.(12分)如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,点P是AB边上一个动点,过点P作AB的垂线交AC边与点D,以PD为边作∠DPE=60°,PE交BC边与点E.
(1)当点D为AC边的中点时,求BE的长;
(2)当PD=PE时,求AP的长;
(3)设AP的长为x,四边形CDPE的面积为y,请直接写出y与x的函数解析式及自变量x的取值范围.
2018-2019学年上海市嘉定区八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共有6题,每小题3分,满分18分)
1.【解答】解:A.=3,与是同类二次根式;
B.=2,与不是同类二次根式;
C.=,与不是同类二次根式;
D.与不是同类二次根式;
故选:A.
2.【解答】解:x2﹣2=0为一元二次方程.
故选:C.
3.【解答】解:选项A,x2﹣2x+2=0,△=4﹣4×2=﹣4<0,方程没有实数根,即x2﹣2x+2在数范围内不能分解因式;
选项B,2x2﹣mx+1=0,△=m2﹣8的值有可能小于0,即2x2﹣mx+1在数范围内不一定能分解因式;
选项C,x2﹣2x+m=0,△=4﹣4m的值有可能小于0,即x2﹣2x+m在数范围内不一定能分解因式;
选项D,x2﹣mx﹣1=0,△=m2+4>0,方程有两个不相等的实数根,即x2﹣mx﹣1在数范围内一定能分解因式.
故选:D.
4.【解答】解:正比例函数y=k1x过一、三象限,故k1>0;
反比例函数y=的图象在二、四象限,故2k2﹣1<0,即k2<.
故选:B.
5.【解答】解:(1)三角形的一条中线能将三角形分成面积相等的两部分,正确;
(2)有两边和其中一边的对角对应相等的两个三角形全等,错误;
(3)点P(1,2)关于原点的对称点坐标为(﹣1,﹣2),正确;
(4)若=a,则a≥0,故本小题错误.
综上所述,正确的是(1)(3).
故选:B.
6.【解答】解:点D是AB的中点,则AD=,
∵AB=2BC,
∴AD=BC,
∵EA⊥AB,CB⊥AB,
∴∠B=∠EAB=90°,
在△AED与△BAC中,
,
∴△AED≌△BAC,
∴∠E=∠CAB,DE=AC,
∴①正确;
∵∠E+∠EDA=90°,
∴∠FAD+∠EDA=90°,
∴∠AFD=180°﹣(∠FAD+∠EDA)=90°,
∴DE⊥AC,
∴②正确;
∵∠EAF与∠ADE都是∠E的余角,
∴∠EAF=∠ADE,
∴③正确;
∵BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,
∴④错误;
故选:C.
二、填空题(本大题共有12题,每小题2分,满分24分)
7.【解答】解:×
=
=
=.
8.【解答】解:原方程可化为:x2﹣4x=0,
∴x(x﹣4)=0
解得x=0或4;
故方程的解为:0,4.
9.【解答】解:由3x2+2x=﹣1得到:3x2+2x+1=0.
∵a=3,b=2,c=1,
∴△=b2﹣4ac=8﹣12=﹣4<0,
∴一元二次方程3x2+2x=﹣1无实数根.
故答案为:无实数根.
10.【解答】解:设九、十月份营业额的月平均增长率为x,
依题意,得:100(1+x)2=144.
故答案为:100(1+x)2=144.
11.【解答】解:∵关于x的方程x2+(m﹣2)x+m2﹣1=0有两个实数根,
∴△=(m﹣2)2﹣4×1×(m2﹣1)=﹣4m+8≥0,
∴m≤2.
故答案为:m≤2.
12.【解答】解:根据题意得:3x﹣2≥0,
解得:x≥.
故答案是:x≥.
13.【解答】解:f(﹣1)==4,
故答案为:4.
14.【解答】解:因为原命题的题设是:“一个三角形是等腰三角形”,结论是“这个三角形两底角相等”,
所以命题“等腰三角形的两个底角相等”的逆命题是“两个角相等三角形是等腰三角形”.
15.【解答】解:根据同圆的半径相等,则圆心应满足到点M和点N的距离相等,即经过已知点M和点N的圆的圆心的轨迹是线段MN的垂直平分线.
故答案为:线段MN的垂直平分线.
16.【解答】解:∵DE是边AB的垂直平分线,
∴DE=CD=10cm,
∵DE⊥AB,∠A=30°,
∴AD=2DE=20cm,
故答案为:20.
17.【解答】解:在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,
∵∠ACB=60°,∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
故答案为∠CHD=45°.
18.【解答】解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
∵,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵AB=5,BE=AC=7,
∴7﹣5<2AD<7+5,即2<2x<12,
∴1<AD<6.
故答案为:1<AD<6.
三、解答题(本大题共7题,满分58分)
19.【解答】解:原式=2+3×﹣(+)
=2+﹣4
=﹣.
20.【解答】解:
3x(x﹣1)﹣2=2x
3x2﹣3x﹣2=2x
3x2﹣5x﹣2=0
(3x+1)(x﹣2)=0
解得:x1=,x2=2
21.【解答】故答案为:y=70x;
(3)爸爸休息之后行走的速度是(3600﹣2100)÷(80﹣50)=50米/分钟,
故答案为:50.
(4)妈妈到达缆车终点的时间为:(分),
爸爸迟到80﹣50﹣8=22(分),
终点时,爸爸离缆车终点的路程为:22×50=1100(米),
故答案为:1100.
22.【解答】证明:∵DE∥BF
∴∠DEF=∠BFE
∵AE=CF
∴AF=CE,且DE=BF,∠DEF=∠BFE
∴△AFB≌△CED(SAS)
∴∠A=∠C
∴AB∥CD
23.【解答】证明:(1)连接CE、BE,
∵ED垂直平分BC,
∴EC=EB,
∵AE平分∠CAB,EF⊥AC,EG⊥AB,
∴EF=EG,
在Rt△CFE和Rt△BGE中,
,
∴Rt△CFE≌Rt△BGE,
∴BG=CF;
(2)∵AE平分∠BAC,EF⊥AC,EG⊥AB,
∴EF=EG,
在Rt△AGE和Rt△AFE中,
,
∴Rt△AGE≌Rt△AFE,
∴AG=AF,
∵AB=AG+BG,
∴AB=AF+CF.
24.【解答】解:(1)∵点(﹣3,﹣4)在反比例函数y=图象上,
∴k1=﹣3×(﹣4)=12.
∵点A(m,2)在反比例函数y=图象上,
∴2m=12,
∴m=6,
∴点A的坐标为(6,2);
∵正比例函数y=k2x(k2≠0)的图象都经过点A(6,2),
∴2=6k2,解得k2,=,
∴正比例函数为y=x;
(2)∵点B(﹣3,n)在正比例函数y=x的图象上,
∴n=﹣3×=﹣1,
∴点B的坐标为(﹣3,﹣1),
∴AB==3.
(3)∵点B的坐标为(﹣3,﹣1),P(﹣3,﹣4),
∴BP=3,
又∵A(6,2),
∴△PAB的面积=BP×h=×3×9=.
25.【解答】解:(1)在△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=AB=2,
∴AC==2,
∵D是AC的中点,
∴AD=,DP=,AP=,
∴BP=AB﹣AP=,
∵∠DPE=60°,
∴∠EPB=30°,
∴EB=BP=;
(2)设AP=x,则BP=4﹣x,
在两个有30°的Rt△APD,Rt△BPE中,AD=2DP,BP=2BE,
由勾股定理解得PD=x,PE=(4﹣x),
因为PD=PE,
所以x=(4﹣x),
解得x=,即AP=;
(3)由(2)知:AP=x,PD=x,PE=(4﹣x),BE=(4﹣x),
∴y=S△ABC﹣S△APD﹣S△BPE
=×2×2﹣?x?x﹣×(4﹣x)?(4﹣x)
=﹣x2+x(0<x<3).
同课章节目录
