湖南省邵阳市2017-2018学年八年级(下)期末数学试卷(解析版)
文档属性
| 名称 | 湖南省邵阳市2017-2018学年八年级(下)期末数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 20:06:45 | ||
图片预览

文档简介
湖南省邵阳市2017-2018学年八年级(下)期末数学试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1.在直角三角形ABC中,∠C=90°,AB=8,CD是AB边上的中线,则CD=( )
A.3 B.4 C.5 D.6
2.下列各组数据中的三个数作为三角形的边长,其中不能构成直角三角形的( )
A.5,12,13 B.3,4,5 C.6,8,10 D.2,3,4
3.若一个多边形的每个内角都等于150°,则这个多边形的边数是( )
A.10 B.11 C.12 D.13
4.如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,则平行四边形ABCD的周长为( )
A.4 B.6 C.8 D.12
5.如图,已知A(2,1),现将A点绕原点O逆时针旋转90°得到A1,则A1的坐标是( )
A.(﹣1,2) B.(2,﹣1) C.(1,﹣2) D.(﹣2,1)
6.下列图形中,是中心对称图形的是( )
A. B.
C. D.
7.张山统计了他家今年3月份打电话的次数及通话时间,并列出如下频数分布表:
通话时间x(分钟) 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数 20 16 9 5
则通话时间不超过15分钟的频率是( )
A.0.4 B.0.6 C.0.7 D.0.9
8.若顺次连接四边形各边中点所得到的四边形是菱形,则该四边形一定是( )
A.矩形
B.对角线相等的四边形
C.正方形
D.对角线互相垂直的四边形
9.将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A.y=﹣3x+2 B.y=﹣3x﹣2 C.y=﹣3(x+2) D.y=﹣3(x﹣2)
10.周大爷每天坚持体育锻炼,某天他慢步到公园,在公园里打了一会儿太极拳,然后跑步回家,下面能反映周大爷离家的距离y与时间x的函数关系的大致图象是( )
A. B.
C. D.
二、填空题(本大题共8小题,每小题3分,满分24分)
11.五边形从某一个顶点出发可以引 条对角线.
12.如图,OC平分∠AOB,P在OC上,PD⊥OA于D,PE⊥OB于E.若PD=3cm,则PE= cm.
13.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若BC=BD,则∠A= 度.
14.如图,菱形ABCD的对角线AC=3cm,BD=4cm,则菱形ABCD的面积是 .
15.如图,将Rt△ABC绕直角顶点A按顺时针方向旋转180°得△AB1C1,写出旋转后BC的对应线段 .
16.某校对n名学生的体育成绩统计如图所示,则n= 人.
17.如图,已知一次函数y=kx+b经过A(2,0),B(0,﹣1),当y>0时,则x的取值范围是 .
18.如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为 米.
三、解答题(19题到25题,每小题8分,26题10分,共66分)
19.如图,在Rt△ABC中,∠C=90°,以点B为圆心,以适当的长为半径画弧,与∠ABC的两边相交于点E、F,分别以点E和点F为圆心,以大于EF的长为半径画弧,两弧相交于点M,作射线BM交AC于点D;若∠ABC=2∠A,证明:AD=2CD.
20.如图,已知平行四边形ABCD中,E、F是对角线BD上的两个点,且BE=DF.
求证:四边形AECF为平行四边形.
21.如图,已知A、B两艘船同时从港口Q出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,它们离开港口2h后相距多远?
22.为了增强学生的身体素质,某校坚持长年的全员体育锻炼,并定期进行体能测试,下面是将某班学生的立定跳远成绩(精确到0.01m),进行整理后,分成5组,画了的频率分布直方图的部分,已知:从左到右4个小组的频率分别是:0.05,0.15,0.30,0.35,第五小组的频数是9.
(1)该班参加测试的人数是多少?
(2)补全频率分布直方图.
(3)若该成绩在2.00m(含2.00)的为合格,问该班成绩合格率是多少?
23.在矩形ABCD中,对角线AC、BD交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°.
(1)求证:△AOB是等边三角形;
(2)求∠BOE的度数.
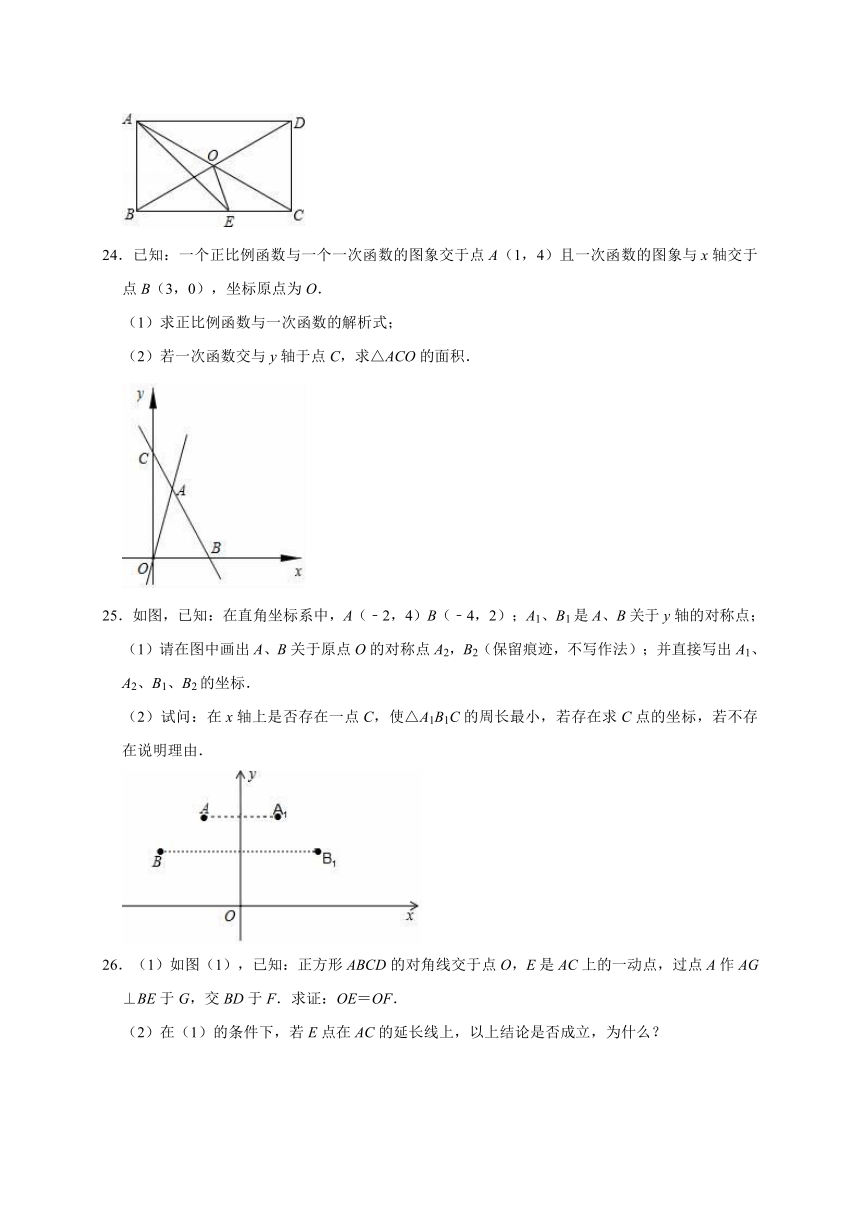
24.已知:一个正比例函数与一个一次函数的图象交于点A(1,4)且一次函数的图象与x轴交于点B(3,0),坐标原点为O.
(1)求正比例函数与一次函数的解析式;
(2)若一次函数交与y轴于点C,求△ACO的面积.
25.如图,已知:在直角坐标系中,A(﹣2,4)B(﹣4,2);A1、B1是A、B关于y轴的对称点;
(1)请在图中画出A、B关于原点O的对称点A2,B2(保留痕迹,不写作法);并直接写出A1、A2、B1、B2的坐标.
(2)试问:在x轴上是否存在一点C,使△A1B1C的周长最小,若存在求C点的坐标,若不存在说明理由.
26.(1)如图(1),已知:正方形ABCD的对角线交于点O,E是AC上的一动点,过点A作AG⊥BE于G,交BD于F.求证:OE=OF.
(2)在(1)的条件下,若E点在AC的延长线上,以上结论是否成立,为什么?
参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,共30分)
1.解:∵∠ACB=90°,AB=8,CD为AB边上的中线,
∴CD=AB=×8=4.
故选:B.
2.解:A、52+122=132,能构成直角三角形,故不符合题意;
B、32+42=52,能构成直角三角形,故不符合题意;
C、62+82=102,能构成直角三角形,故不符合题意;
D、22+32≠42,不能构成直角三角形,故符合题意.
故选:D.
3.解:由题意可得:180°?(n﹣2)=150°?n,
解得n=12.
故多边形是12边形.
故选:C.
4.解:∵四边形ABCD为平行四边形,
∴∠1=∠4,∠2=∠3,
∵AC平分∠DAB,
∴∠1=∠2,
∴∠1=∠3,
∴AD=DC,
四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.
故选:C.
5.解:将A点绕原点O逆时针旋转90°得到A1,
即将Rt△OBA点绕原点O逆时针旋转90°得到Rt△OB1A1,如图,
所以OB1=OB=2,A1B1=AB=1,
所以点A1的坐标是(﹣1,2).
故选:A.
6.解:A、不是中心对称图形,故本选项错误;
B、不是中心对称图形,故本选项错误;
C、是中心对称图形,不是轴对称图形,故本选项正确;
D、不是中心对称图形,故本选项错误.
故选:C.
7.解:由表格可得,通话时间不超过15分钟的频率是:=0.9,
故选:D.
8.解:∵点E,F,G,H分别是边AD,AB,BC,CD的中点,
∴EH∥AC,EH=AC,FG∥AC,FG=AC,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
根据题意得:四边形EFGH是菱形,
∴EF=EH,
∴AC=BD,
∴原四边形一定是对角线相等的四边形.
故选:B.
9.解:根据平移的规律可知:平移后的函数关系式为y=﹣3x+2.
故选:A.
10.解:图象应分三个阶段,第一阶段:慢步到离家较远的公园,在这个阶段,离家的距离随时间的增大而增大;
第二阶段:打了一会儿太极拳,这一阶段离家的距离不随时间的变化而改变.故D错误;
第三阶段:跑步回家,这一阶段,离家的距离随时间的增大而减小,故A错误,并且这段的速度大于第一阶段的速度,则B错误.
故选:C.
二、填空题(本大题共8小题,每小题3分,满分24分)
11.解:从五边形的一个顶点出发有5﹣3=2条对角线,
故答案为:2.
12.解:∵OC平分∠AOB,PD⊥OA,PE⊥OB,
∴PE=PD=3cm.
故答案为;3
13.解:∵在Rt△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD,
∵BC=BD,
∴CD=BC=BD,
∴△BCD是等边三角形,
∴∠B=60度,
∴∠A=30度.
故答案为:30.
14.解:因为菱形的对角线互相垂直平分,
∵AC=3cm,BD=4cm,
则菱形ABCD的面积是cm2.
故答案为12cm2.
15.解:
∵将Rt△ABC绕直角顶点A按顺时针方向旋转180°得△AB1C1,
∴△ABC≌△AB1C1,
∴BC=B1C1,
∴旋转后BC的对应线段是B1C1,
故答案为:B1C1.
16.解:由统计图可得,
n=20+30+10=60(人),
故答案为:60.
17.解:由A(2,0),B(0,﹣1),可得直线AB的解析式为y=x﹣1,
∴当y>0时, x﹣1>0,
解得x>2,
故答案为:x>2.
18.解:过点C作CE⊥AB,交AB的延长线于E,如右图,
∵∠ABC=150°,
∴∠CBE=30°,
在Rt△BCE中,∵BC=12,∠CBE=30°,
∴CE=BC=6.
故答案是6.
三、解答题(19题到25题,每小题8分,26题10分,共66分)
19.证明:由题意可得:BD是∠ABC的角平分线,
∵∠ABC=2∠A,在Rt△ABC中,∠C=90°,
∴∠ABC=60°,∠A=30°,
∴∠CBD=∠DBA=30°,
∴BD=2CD,
∵∠DBA=∠A=30°,
∴AD=BD,
∴AD=2CD.
20.证明:连接对角线AC交对角线BD于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵点E,F是对角线BD上的两点,且BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
∴四边形AECF是平行四边形.
21.解:∵A、B两艘船同时从港口O出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,
∴∠AOB=90°,它们离开港口2h后,AO=40×2=80km,BO=30×2=60km,
∴AB==100km,
答:它们离开港口2h后相距100km.
22.解:(1)9÷(1﹣0.05﹣0.15﹣0.30﹣0.35)=60(人)
答:参加测试的有60人;
(2)第五组的频率是:1﹣0.05﹣0.15﹣0.30﹣0.35=0.15,
补全的频率分布直方图如右图所示;
(3)0.30+0.35+0.15=0.80,
答:该班成绩合格率是0.80.
23.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°,
∴OA=OB,∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°=∠AEB,
∴AB=BE,
∵∠CAE=15°,
∴∠DAC=45°﹣15°=30°,
∠BAC=60°,
∴△BAO是等边三角形.
(2)∵△AOB是等边三角形,
∴AB=OB,∠ABO=60°,
∴∠OBC=90°﹣60°=30°,
∵AB=OB=BE,
∴∠BOE=∠BEO=(180°﹣30°)=75°.
24.解:(1)设正比例函数解析式为y=mx,
∵图象经过点A(1,4),
∴4=m×1,即m=4,
∴正比例函数解析式为y=4x;
设一次函数解析式为y=kx+b,
∵图象经过(1,4)(3,0),
∴,
解得:,
∴一次函数解析式为y=﹣2x+6.
(2)在y=﹣2x+6中,令x=0,则y=6,
∴C(0,6),
∴OC=6,
∴S△AOC=×6×1=3.
25.解:(1)如图,点A2,B2为所作,点A1、A2、B1、B2的坐标分别为(2,4),(4,2),(2,﹣4),(4,﹣2);
(2)存在.
连接A1B2交x轴于C,如图,
∵点B1与B2关于x轴对称,
∴CB1=CB2,
∴CA1+CB1=CA1+CB2=A1B2,
此时CA1+CB1的值最小,则△A1B1C的周长最小,
设直线A1B2的解析式为y=kx+b,
把A1(2,4),B2(4,﹣2)代入得,解得,
∴直线A1B2的解析式为y=﹣3x+10,
当y=0时,﹣3x+10=0,解得x=,
∴C点坐标为(,0).
26.(1)证明:∵四边形ABCD为正方形,
∴OA=OB,∠AOB=∠BOC=90°,
∵AG⊥BE于点G,
∴∠AGE=90°,
∴∠GAE=∠OBE,
在△AOF和△BOE中
,
∴△AOF≌△BOE(ASA),
∴OF=OE;
(2)解:以上结论仍然成立.理由如下:
同样可证明△AOF≌△BOE(ASA),所以OF=OE.
一、选择题(本大题共10小题,每小题3分,共30分)
1.在直角三角形ABC中,∠C=90°,AB=8,CD是AB边上的中线,则CD=( )
A.3 B.4 C.5 D.6
2.下列各组数据中的三个数作为三角形的边长,其中不能构成直角三角形的( )
A.5,12,13 B.3,4,5 C.6,8,10 D.2,3,4
3.若一个多边形的每个内角都等于150°,则这个多边形的边数是( )
A.10 B.11 C.12 D.13
4.如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,则平行四边形ABCD的周长为( )
A.4 B.6 C.8 D.12
5.如图,已知A(2,1),现将A点绕原点O逆时针旋转90°得到A1,则A1的坐标是( )
A.(﹣1,2) B.(2,﹣1) C.(1,﹣2) D.(﹣2,1)
6.下列图形中,是中心对称图形的是( )
A. B.
C. D.
7.张山统计了他家今年3月份打电话的次数及通话时间,并列出如下频数分布表:
通话时间x(分钟) 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数 20 16 9 5
则通话时间不超过15分钟的频率是( )
A.0.4 B.0.6 C.0.7 D.0.9
8.若顺次连接四边形各边中点所得到的四边形是菱形,则该四边形一定是( )
A.矩形
B.对角线相等的四边形
C.正方形
D.对角线互相垂直的四边形
9.将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A.y=﹣3x+2 B.y=﹣3x﹣2 C.y=﹣3(x+2) D.y=﹣3(x﹣2)
10.周大爷每天坚持体育锻炼,某天他慢步到公园,在公园里打了一会儿太极拳,然后跑步回家,下面能反映周大爷离家的距离y与时间x的函数关系的大致图象是( )
A. B.
C. D.
二、填空题(本大题共8小题,每小题3分,满分24分)
11.五边形从某一个顶点出发可以引 条对角线.
12.如图,OC平分∠AOB,P在OC上,PD⊥OA于D,PE⊥OB于E.若PD=3cm,则PE= cm.
13.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若BC=BD,则∠A= 度.
14.如图,菱形ABCD的对角线AC=3cm,BD=4cm,则菱形ABCD的面积是 .
15.如图,将Rt△ABC绕直角顶点A按顺时针方向旋转180°得△AB1C1,写出旋转后BC的对应线段 .
16.某校对n名学生的体育成绩统计如图所示,则n= 人.
17.如图,已知一次函数y=kx+b经过A(2,0),B(0,﹣1),当y>0时,则x的取值范围是 .
18.如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为 米.
三、解答题(19题到25题,每小题8分,26题10分,共66分)
19.如图,在Rt△ABC中,∠C=90°,以点B为圆心,以适当的长为半径画弧,与∠ABC的两边相交于点E、F,分别以点E和点F为圆心,以大于EF的长为半径画弧,两弧相交于点M,作射线BM交AC于点D;若∠ABC=2∠A,证明:AD=2CD.
20.如图,已知平行四边形ABCD中,E、F是对角线BD上的两个点,且BE=DF.
求证:四边形AECF为平行四边形.
21.如图,已知A、B两艘船同时从港口Q出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,它们离开港口2h后相距多远?
22.为了增强学生的身体素质,某校坚持长年的全员体育锻炼,并定期进行体能测试,下面是将某班学生的立定跳远成绩(精确到0.01m),进行整理后,分成5组,画了的频率分布直方图的部分,已知:从左到右4个小组的频率分别是:0.05,0.15,0.30,0.35,第五小组的频数是9.
(1)该班参加测试的人数是多少?
(2)补全频率分布直方图.
(3)若该成绩在2.00m(含2.00)的为合格,问该班成绩合格率是多少?
23.在矩形ABCD中,对角线AC、BD交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°.
(1)求证:△AOB是等边三角形;
(2)求∠BOE的度数.
24.已知:一个正比例函数与一个一次函数的图象交于点A(1,4)且一次函数的图象与x轴交于点B(3,0),坐标原点为O.
(1)求正比例函数与一次函数的解析式;
(2)若一次函数交与y轴于点C,求△ACO的面积.
25.如图,已知:在直角坐标系中,A(﹣2,4)B(﹣4,2);A1、B1是A、B关于y轴的对称点;
(1)请在图中画出A、B关于原点O的对称点A2,B2(保留痕迹,不写作法);并直接写出A1、A2、B1、B2的坐标.
(2)试问:在x轴上是否存在一点C,使△A1B1C的周长最小,若存在求C点的坐标,若不存在说明理由.
26.(1)如图(1),已知:正方形ABCD的对角线交于点O,E是AC上的一动点,过点A作AG⊥BE于G,交BD于F.求证:OE=OF.
(2)在(1)的条件下,若E点在AC的延长线上,以上结论是否成立,为什么?
参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,共30分)
1.解:∵∠ACB=90°,AB=8,CD为AB边上的中线,
∴CD=AB=×8=4.
故选:B.
2.解:A、52+122=132,能构成直角三角形,故不符合题意;
B、32+42=52,能构成直角三角形,故不符合题意;
C、62+82=102,能构成直角三角形,故不符合题意;
D、22+32≠42,不能构成直角三角形,故符合题意.
故选:D.
3.解:由题意可得:180°?(n﹣2)=150°?n,
解得n=12.
故多边形是12边形.
故选:C.
4.解:∵四边形ABCD为平行四边形,
∴∠1=∠4,∠2=∠3,
∵AC平分∠DAB,
∴∠1=∠2,
∴∠1=∠3,
∴AD=DC,
四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.
故选:C.
5.解:将A点绕原点O逆时针旋转90°得到A1,
即将Rt△OBA点绕原点O逆时针旋转90°得到Rt△OB1A1,如图,
所以OB1=OB=2,A1B1=AB=1,
所以点A1的坐标是(﹣1,2).
故选:A.
6.解:A、不是中心对称图形,故本选项错误;
B、不是中心对称图形,故本选项错误;
C、是中心对称图形,不是轴对称图形,故本选项正确;
D、不是中心对称图形,故本选项错误.
故选:C.
7.解:由表格可得,通话时间不超过15分钟的频率是:=0.9,
故选:D.
8.解:∵点E,F,G,H分别是边AD,AB,BC,CD的中点,
∴EH∥AC,EH=AC,FG∥AC,FG=AC,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
根据题意得:四边形EFGH是菱形,
∴EF=EH,
∴AC=BD,
∴原四边形一定是对角线相等的四边形.
故选:B.
9.解:根据平移的规律可知:平移后的函数关系式为y=﹣3x+2.
故选:A.
10.解:图象应分三个阶段,第一阶段:慢步到离家较远的公园,在这个阶段,离家的距离随时间的增大而增大;
第二阶段:打了一会儿太极拳,这一阶段离家的距离不随时间的变化而改变.故D错误;
第三阶段:跑步回家,这一阶段,离家的距离随时间的增大而减小,故A错误,并且这段的速度大于第一阶段的速度,则B错误.
故选:C.
二、填空题(本大题共8小题,每小题3分,满分24分)
11.解:从五边形的一个顶点出发有5﹣3=2条对角线,
故答案为:2.
12.解:∵OC平分∠AOB,PD⊥OA,PE⊥OB,
∴PE=PD=3cm.
故答案为;3
13.解:∵在Rt△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD,
∵BC=BD,
∴CD=BC=BD,
∴△BCD是等边三角形,
∴∠B=60度,
∴∠A=30度.
故答案为:30.
14.解:因为菱形的对角线互相垂直平分,
∵AC=3cm,BD=4cm,
则菱形ABCD的面积是cm2.
故答案为12cm2.
15.解:
∵将Rt△ABC绕直角顶点A按顺时针方向旋转180°得△AB1C1,
∴△ABC≌△AB1C1,
∴BC=B1C1,
∴旋转后BC的对应线段是B1C1,
故答案为:B1C1.
16.解:由统计图可得,
n=20+30+10=60(人),
故答案为:60.
17.解:由A(2,0),B(0,﹣1),可得直线AB的解析式为y=x﹣1,
∴当y>0时, x﹣1>0,
解得x>2,
故答案为:x>2.
18.解:过点C作CE⊥AB,交AB的延长线于E,如右图,
∵∠ABC=150°,
∴∠CBE=30°,
在Rt△BCE中,∵BC=12,∠CBE=30°,
∴CE=BC=6.
故答案是6.
三、解答题(19题到25题,每小题8分,26题10分,共66分)
19.证明:由题意可得:BD是∠ABC的角平分线,
∵∠ABC=2∠A,在Rt△ABC中,∠C=90°,
∴∠ABC=60°,∠A=30°,
∴∠CBD=∠DBA=30°,
∴BD=2CD,
∵∠DBA=∠A=30°,
∴AD=BD,
∴AD=2CD.
20.证明:连接对角线AC交对角线BD于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵点E,F是对角线BD上的两点,且BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
∴四边形AECF是平行四边形.
21.解:∵A、B两艘船同时从港口O出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,
∴∠AOB=90°,它们离开港口2h后,AO=40×2=80km,BO=30×2=60km,
∴AB==100km,
答:它们离开港口2h后相距100km.
22.解:(1)9÷(1﹣0.05﹣0.15﹣0.30﹣0.35)=60(人)
答:参加测试的有60人;
(2)第五组的频率是:1﹣0.05﹣0.15﹣0.30﹣0.35=0.15,
补全的频率分布直方图如右图所示;
(3)0.30+0.35+0.15=0.80,
答:该班成绩合格率是0.80.
23.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°,
∴OA=OB,∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°=∠AEB,
∴AB=BE,
∵∠CAE=15°,
∴∠DAC=45°﹣15°=30°,
∠BAC=60°,
∴△BAO是等边三角形.
(2)∵△AOB是等边三角形,
∴AB=OB,∠ABO=60°,
∴∠OBC=90°﹣60°=30°,
∵AB=OB=BE,
∴∠BOE=∠BEO=(180°﹣30°)=75°.
24.解:(1)设正比例函数解析式为y=mx,
∵图象经过点A(1,4),
∴4=m×1,即m=4,
∴正比例函数解析式为y=4x;
设一次函数解析式为y=kx+b,
∵图象经过(1,4)(3,0),
∴,
解得:,
∴一次函数解析式为y=﹣2x+6.
(2)在y=﹣2x+6中,令x=0,则y=6,
∴C(0,6),
∴OC=6,
∴S△AOC=×6×1=3.
25.解:(1)如图,点A2,B2为所作,点A1、A2、B1、B2的坐标分别为(2,4),(4,2),(2,﹣4),(4,﹣2);
(2)存在.
连接A1B2交x轴于C,如图,
∵点B1与B2关于x轴对称,
∴CB1=CB2,
∴CA1+CB1=CA1+CB2=A1B2,
此时CA1+CB1的值最小,则△A1B1C的周长最小,
设直线A1B2的解析式为y=kx+b,
把A1(2,4),B2(4,﹣2)代入得,解得,
∴直线A1B2的解析式为y=﹣3x+10,
当y=0时,﹣3x+10=0,解得x=,
∴C点坐标为(,0).
26.(1)证明:∵四边形ABCD为正方形,
∴OA=OB,∠AOB=∠BOC=90°,
∵AG⊥BE于点G,
∴∠AGE=90°,
∴∠GAE=∠OBE,
在△AOF和△BOE中
,
∴△AOF≌△BOE(ASA),
∴OF=OE;
(2)解:以上结论仍然成立.理由如下:
同样可证明△AOF≌△BOE(ASA),所以OF=OE.
同课章节目录
