湖南省邵阳市武冈市2017-2018学年八年级(下)期末数学试卷含解析
文档属性
| 名称 | 湖南省邵阳市武冈市2017-2018学年八年级(下)期末数学试卷含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 283.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 20:31:37 | ||
图片预览


文档简介
湖南省邵阳市武冈市2017-2018学年八年级(下)期末数学试卷
一、细心选一选(将正确答案的序号填在对应的题号下面,本大题共10小题,每小题3分,共30分)
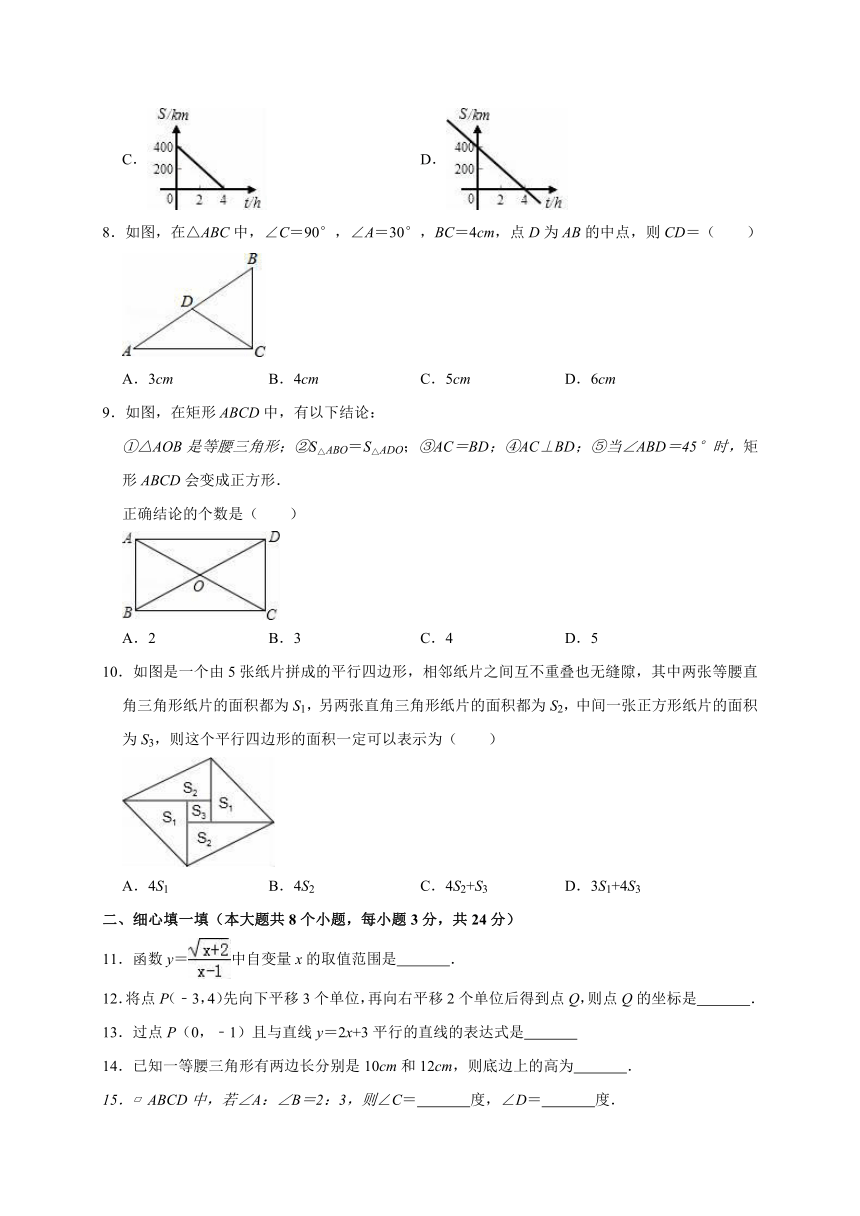
1.下列图形中既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.以下列各组数为边长能构成直角三角形的是( )
A.1,1, B.2,3,4 C.4,5,6 D.6,8,11
3.在平面直角坐标系中,点M到x轴的距离是3,到y轴的距离是2,且在第二象限,则点M的坐标是( )
A.(3,﹣2) B.(﹣2,3) C.(﹣3,2) D.(﹣2,﹣3)
4.已知直线y=2x+4与x轴交于点A,与y轴交于点B,则△AOB面积为( )
A.8 B.6 C.4 D.2
5.一次函数y=kx+k的图象可能是( )
A. B.
C. D.
6.一组数据的最大值与最小值的差为80,若确定组距为9,则分成的组数为( )
A.7 B.8 C.9 D.12
7.汽车由重庆驶往相距400千米的成都,如果汽车的平均速度是100千米/时,那么汽车距成都的路程s(千米)与行驶时间t(小时)的函数关系用图象表示为( )
A. B.
C. D.
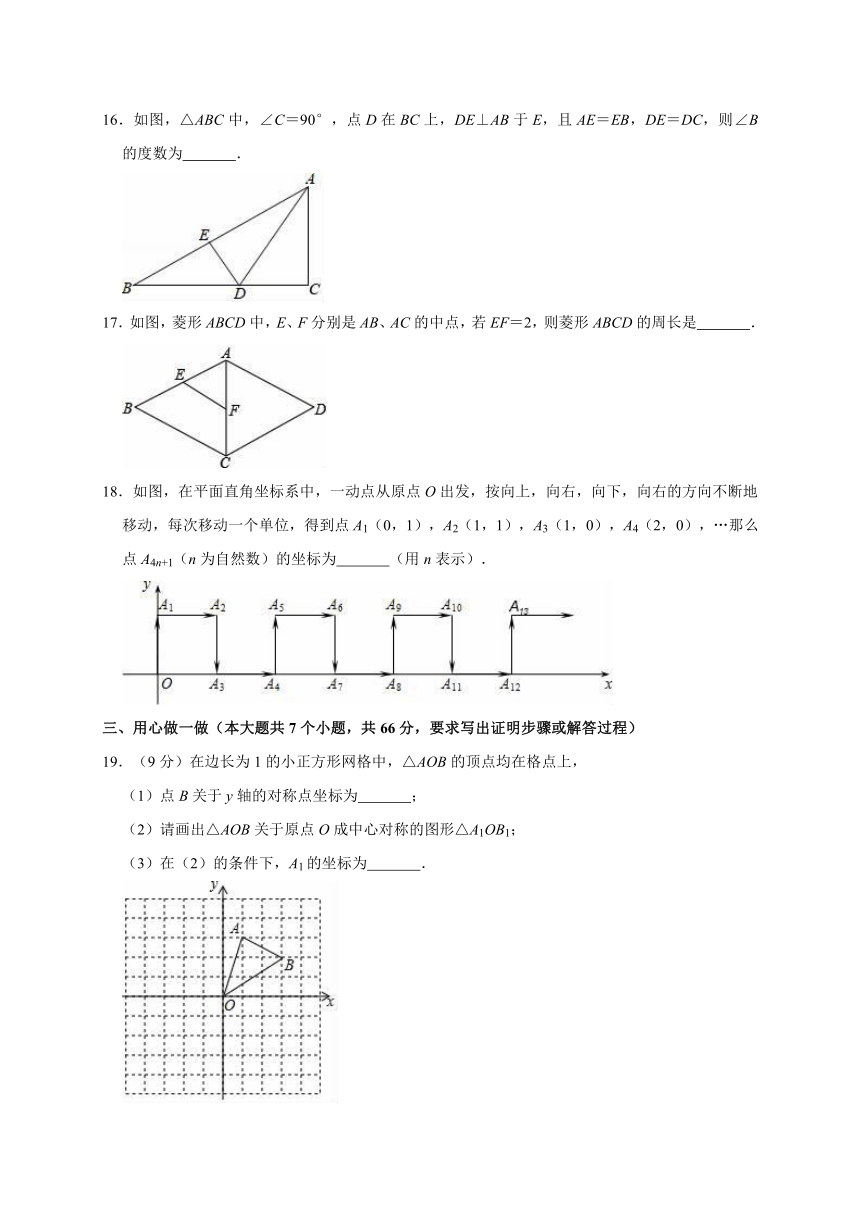
8.如图,在△ABC中,∠C=90°,∠A=30°,BC=4cm,点D为AB的中点,则CD=( )
A.3cm B.4cm C.5cm D.6cm
9.如图,在矩形ABCD中,有以下结论:
①△AOB是等腰三角形;②S△ABO=S△ADO;③AC=BD;④AC⊥BD;⑤当∠ABD=45°时,矩形ABCD会变成正方形.
正确结论的个数是( )
A.2 B.3 C.4 D.5
10.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1 B.4S2 C.4S2+S3 D.3S1+4S3
二、细心填一填(本大题共8个小题,每小题3分,共24分)
11.函数y=中自变量x的取值范围是 .
12.将点P(﹣3,4)先向下平移3个单位,再向右平移2个单位后得到点Q,则点Q的坐标是 .
13.过点P(0,﹣1)且与直线y=2x+3平行的直线的表达式是
14.已知一等腰三角形有两边长分别是10cm和12cm,则底边上的高为 .
15.?ABCD中,若∠A:∠B=2:3,则∠C= 度,∠D= 度.
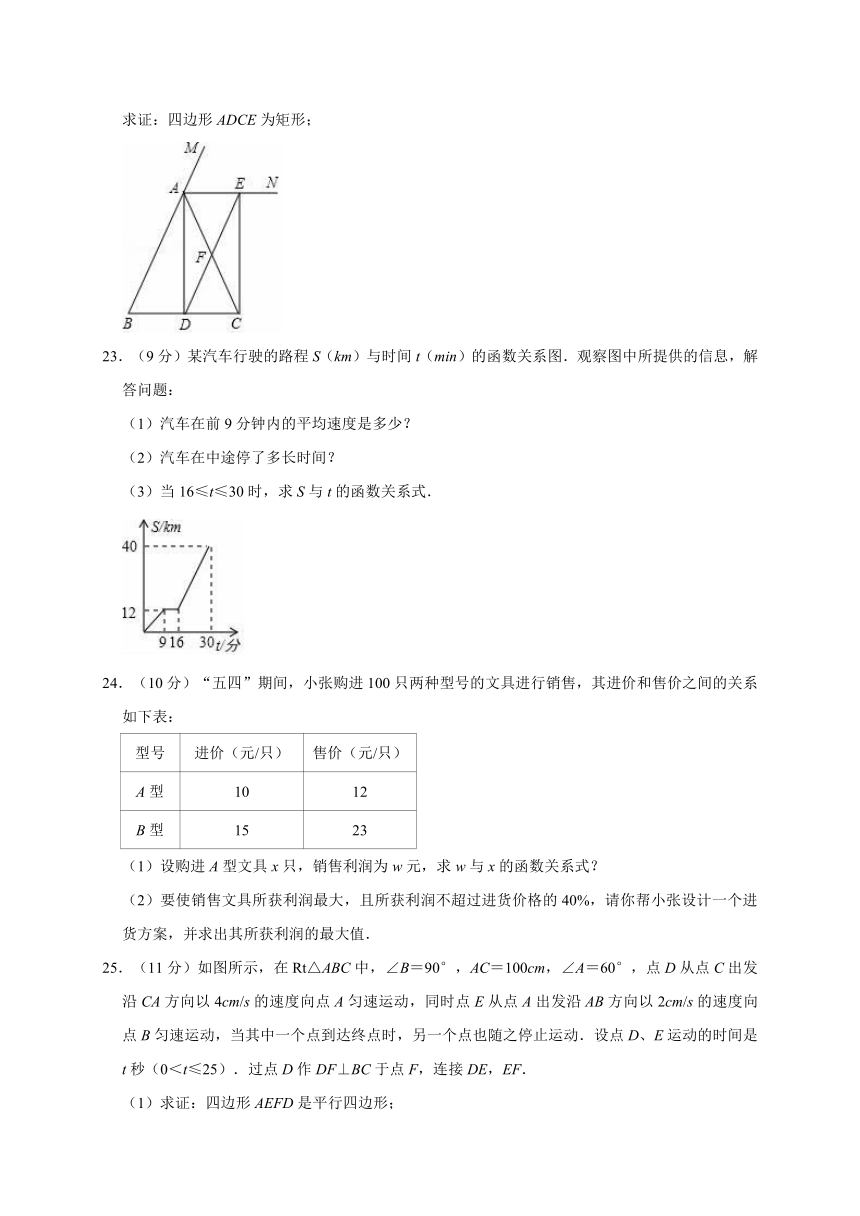
16.如图,△ABC中,∠C=90°,点D在BC上,DE⊥AB于E,且AE=EB,DE=DC,则∠B的度数为 .
17.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=2,则菱形ABCD的周长是 .
18.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示).
三、用心做一做(本大题共7个小题,共66分,要求写出证明步骤或解答过程)
19.(9分)在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)点B关于y轴的对称点坐标为 ;
(2)请画出△AOB关于原点O成中心对称的图形△A1OB1;
(3)在(2)的条件下,A1的坐标为 .
20.(9分)为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 成绩x分 频数(人数)
第1组 25≤x<30 4
第2组 30≤x<35 6
第3组 35≤x<40 14
第4组 40≤x<45 a
第5组 45≤x<50 10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
21.(10分)如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
求证:(1)△ADE≌△BEC
(2)△CDE是直角三角形.
22.(8分)已知:如图,在△ABC中,AB=AC,AD是∠BAC的平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
求证:四边形ADCE为矩形;
23.(9分)某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.
24.(10分)“五四”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 进价(元/只) 售价(元/只)
A型 10 12
B型 15 23
(1)设购进A型文具x只,销售利润为w元,求w与x的函数关系式?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
25.(11分)如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
参考答案与试题解析
一、细心选一选(将正确答案的序号填在对应的题号下面,本大题共10小题,每小题3分,共30分)
1.解:A、是中心对称图形,不是轴对称图形,故本选项错误;
B、是中心对称图形,不是轴对称图形,故本选项错误;
C、既是中心对称图形,又是轴对称图形,故本选项正确;
D、是中心对称图形,不是轴对称图形,故本选项错误.
故选:C.
2.解:A、∵12+12=2=()2,∴能构成直角三角形,故本选项正确;
B、∵22+32=25≠42,∴不能构成直角三角形,故本选项错误;
C、∵42+52=41≠62,∴不能构成直角三角形,故本选项错误;
D、∵62+82=100≠112,∴不能构成直角三角形,故本选项错误.
故选:A.
3.解:由题意,得
|y|=3,|x|=2,
点M到x轴的距离是3,到y轴的距离是2,且在第二象限,得
x=﹣2,y=3,
则点M的坐标是(﹣2,3),
故选:B.
4.解:∵直线y=2x+4与x轴交于点A,与y轴交于点B,
∴A(﹣2,0),B(0,4),
∴OA=2,OB=4,
∴S△AOB=?OA?OB=×2×4=4;
故选:C.
5.解:当k>0时,函数图象经过一、二、三象限;
当k<0时,函数图象经过二、三、四象限,故B正确.
故选:B.
6.解:在样本数据中最大值与最小值的差为80,已知组距为9,那么由于=8,故可以分成9组.
故选:C.
7.解:根据题意可知s=400﹣100t(0≤t≤4),
∴与坐标轴的交点坐标为(0,400),(4,0).
要注意x、y的取值范围(0≤t≤4,0≤y≤400).
故选:C.
8.解:∵∠C=90°,∠A=30°,BC=4cm,
∴AB=2BC=8cm,
∵点D为AB的中点,
∴CD=4cm,
故选:B.
9.解:∵四边形ABCD是矩形,
∴AO=BO=DO=CO,AC=BD,故①③正确;
∵BO=DO,
∴S△ABO=S△ADO,故②正确;
当∠ABD=45°时,
则∠AOD=90°,
∴AC⊥BD,
∴矩形ABCD变成正方形,故⑤正确,
而④不一定正确,矩形的对角线只是相等,
∴正确结论的个数是4个.
故选:C.
10.解:设等腰直角三角形的直角边为a,正方形边长为c,
则S2=(a+c)(a﹣c)=a2﹣c2,
∴S2=S1﹣S3,
∴S3=2S1﹣2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1.
故选:A.
二、细心填一填(本大题共8个小题,每小题3分,共24分)
11.解:由题意得,x+2≥0且x﹣1≠0,
解得x≥﹣2且x≠1.
故答案为:x≥﹣2且x≠1.
12.解:根据题意,知点Q的坐标是(﹣3+2,4﹣3),即(﹣1,1),
故答案为:(﹣1,1).
13.解:设所求的一次函数解析式为y=kx+b,
∵直线y=kx+b与y=2x+3平行,
∴k=2,
∵点P(0,﹣1)在直线y=2x+b上,
∴﹣0+b=﹣1,解得b=﹣1,
∴所求的一次函数解析式为y=2x﹣1.
故答案为y=2x﹣1.
14.解:作AD⊥BC于D,
当AB=AC=10,BC=12时,BD=BC=6,
底边上的高AD==8,
当AB=AC=12,BC=10时,BD=BC=5,
底边上的高AD==,
故答案为:8cm或cm.
15.解:根据平行四边形的性质可知,∠A+∠B=180°,
∵∠A:∠B=2:3,
∴∠A=72°,∠B=108°
∴∠C=72°,∠D=108°.
故答案为72,108.
16.解:∵AE=EB,DE⊥AB,
∴DA=DB,
∴∠B=∠DAE,
∵DE⊥AB,DC⊥AC,DE=DC,
∴∠DAE=∠DAC,
∴∠B=∠BAD=∠CAD=30°,
故答案为30°.
17.解:∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴BC=2EF=2×2=4,
∴菱形ABCD的周长=4BC=4×4=16.
故答案为16.
18.解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
三、用心做一做(本大题共7个小题,共66分,要求写出证明步骤或解答过程)
19.解:(1)点B关于y轴的对称点坐标为(﹣3,2);
(2)如图所示,△A1OB1即为所求;
(3)在(2)的条件下,A1的坐标为(﹣1,﹣3).
故答案为:(1)(﹣3,2);(3)(﹣1,﹣3)
20.解:(1)a=50﹣4﹣6﹣14﹣10=16;
(2)如图所示:
(3)本次测试的优秀率是:×100%=52%.
21.证明:(1)∵∠1=∠2,
∴DE=CE,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
∴Rt△ADE≌Rt△BEC(HL);
(2)∵Rt△ADE≌Rt△BEC,
∴∠3=∠4,
∵∠3+∠5=90°,
∴∠4+∠5=90°,
∴∠DEC=90°,
∴△CDE是直角三角形.
22.证明:∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,∠BAD=∠CAD.
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN.
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°.
∴四边形ADCE为矩形.
23.解:(1)由图可得,
汽车在前9分钟内的平均速度是:12÷9=km/min;
(2)由图可得,
汽车在中途停了:16﹣9=7min,
即汽车在中途停了7min;
(3)设当16≤t≤30时,S与t的函数关系式是S=at+b,
,得,
即当16≤t≤30时,S与t的函数关系式是S=2t﹣20.
24.解:(1)由题意可得,
w=(12﹣10)x+(23﹣15)(100﹣x)=﹣6x+800
∴w与x之间的函数关系式为w=﹣6x+800;
(2)由题意可得,
﹣6x+800≤40%[10x+15(100﹣x)]
解得:x≥50
又由(1)得:w=﹣6x+800,k=﹣6<0,
∴w随x的增大而减小
∴当x=50时,w达到最大值,即最大利润w=﹣50×6+800=500元,
此时100﹣x=100﹣50=50只
答:购进A型文具50只,B型文具50只时所获利润最大,利润最大为500元.
25.证明:(1)由题意得:AE=2t,CD=4t,
∵DF⊥BC,
∴∠CFD=90°,
∵∠C=30°,
∴DF=CD=×4t=2t,
∴AE=DF;
∵DF⊥BC,
∴∠CFD=∠B=90°,
∴DF∥AE,
∴四边形AEFD是平行四边形.
(2)四边形AEFD能够成为菱形,理由是:
由(1)得:AE=DF,
∵∠DFC=∠B=90°,
∴AE∥DF,
∴四边形AEFD为平行四边形,
若?AEFD为菱形,则AE=AD,
∵AC=100,CD=4t,
∴AD=100﹣4t,
∴2t=100﹣4t,
t=,
∴当t=时,四边形AEFD能够成为菱形;
(3)分三种情况:
①当∠EDF=90°时,如图3,
则四边形DFBE为矩形,
∴DF=BE=2t,
∵AB=AC=50,AE=2t,
∴2t=50﹣2t,
t=,
②当∠DEF=90°时,如图4,
∵四边形AEFD为平行四边形,
∴EF∥AD,
∴∠ADE=∠DEF=90°,
在Rt△ADE中,∠A=60°,AE=2t,
∴AD=t,
∴AC=AD+CD,
则100=t+4t,
t=20,
③当∠DFE=90°不成立;
综上所述:当t为或20时,△DEF为直角三角形.
一、细心选一选(将正确答案的序号填在对应的题号下面,本大题共10小题,每小题3分,共30分)
1.下列图形中既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.以下列各组数为边长能构成直角三角形的是( )
A.1,1, B.2,3,4 C.4,5,6 D.6,8,11
3.在平面直角坐标系中,点M到x轴的距离是3,到y轴的距离是2,且在第二象限,则点M的坐标是( )
A.(3,﹣2) B.(﹣2,3) C.(﹣3,2) D.(﹣2,﹣3)
4.已知直线y=2x+4与x轴交于点A,与y轴交于点B,则△AOB面积为( )
A.8 B.6 C.4 D.2
5.一次函数y=kx+k的图象可能是( )
A. B.
C. D.
6.一组数据的最大值与最小值的差为80,若确定组距为9,则分成的组数为( )
A.7 B.8 C.9 D.12
7.汽车由重庆驶往相距400千米的成都,如果汽车的平均速度是100千米/时,那么汽车距成都的路程s(千米)与行驶时间t(小时)的函数关系用图象表示为( )
A. B.
C. D.
8.如图,在△ABC中,∠C=90°,∠A=30°,BC=4cm,点D为AB的中点,则CD=( )
A.3cm B.4cm C.5cm D.6cm
9.如图,在矩形ABCD中,有以下结论:
①△AOB是等腰三角形;②S△ABO=S△ADO;③AC=BD;④AC⊥BD;⑤当∠ABD=45°时,矩形ABCD会变成正方形.
正确结论的个数是( )
A.2 B.3 C.4 D.5
10.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1 B.4S2 C.4S2+S3 D.3S1+4S3
二、细心填一填(本大题共8个小题,每小题3分,共24分)
11.函数y=中自变量x的取值范围是 .
12.将点P(﹣3,4)先向下平移3个单位,再向右平移2个单位后得到点Q,则点Q的坐标是 .
13.过点P(0,﹣1)且与直线y=2x+3平行的直线的表达式是
14.已知一等腰三角形有两边长分别是10cm和12cm,则底边上的高为 .
15.?ABCD中,若∠A:∠B=2:3,则∠C= 度,∠D= 度.
16.如图,△ABC中,∠C=90°,点D在BC上,DE⊥AB于E,且AE=EB,DE=DC,则∠B的度数为 .
17.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=2,则菱形ABCD的周长是 .
18.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示).
三、用心做一做(本大题共7个小题,共66分,要求写出证明步骤或解答过程)
19.(9分)在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)点B关于y轴的对称点坐标为 ;
(2)请画出△AOB关于原点O成中心对称的图形△A1OB1;
(3)在(2)的条件下,A1的坐标为 .
20.(9分)为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 成绩x分 频数(人数)
第1组 25≤x<30 4
第2组 30≤x<35 6
第3组 35≤x<40 14
第4组 40≤x<45 a
第5组 45≤x<50 10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
21.(10分)如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
求证:(1)△ADE≌△BEC
(2)△CDE是直角三角形.
22.(8分)已知:如图,在△ABC中,AB=AC,AD是∠BAC的平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
求证:四边形ADCE为矩形;
23.(9分)某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.
24.(10分)“五四”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 进价(元/只) 售价(元/只)
A型 10 12
B型 15 23
(1)设购进A型文具x只,销售利润为w元,求w与x的函数关系式?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
25.(11分)如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
参考答案与试题解析
一、细心选一选(将正确答案的序号填在对应的题号下面,本大题共10小题,每小题3分,共30分)
1.解:A、是中心对称图形,不是轴对称图形,故本选项错误;
B、是中心对称图形,不是轴对称图形,故本选项错误;
C、既是中心对称图形,又是轴对称图形,故本选项正确;
D、是中心对称图形,不是轴对称图形,故本选项错误.
故选:C.
2.解:A、∵12+12=2=()2,∴能构成直角三角形,故本选项正确;
B、∵22+32=25≠42,∴不能构成直角三角形,故本选项错误;
C、∵42+52=41≠62,∴不能构成直角三角形,故本选项错误;
D、∵62+82=100≠112,∴不能构成直角三角形,故本选项错误.
故选:A.
3.解:由题意,得
|y|=3,|x|=2,
点M到x轴的距离是3,到y轴的距离是2,且在第二象限,得
x=﹣2,y=3,
则点M的坐标是(﹣2,3),
故选:B.
4.解:∵直线y=2x+4与x轴交于点A,与y轴交于点B,
∴A(﹣2,0),B(0,4),
∴OA=2,OB=4,
∴S△AOB=?OA?OB=×2×4=4;
故选:C.
5.解:当k>0时,函数图象经过一、二、三象限;
当k<0时,函数图象经过二、三、四象限,故B正确.
故选:B.
6.解:在样本数据中最大值与最小值的差为80,已知组距为9,那么由于=8,故可以分成9组.
故选:C.
7.解:根据题意可知s=400﹣100t(0≤t≤4),
∴与坐标轴的交点坐标为(0,400),(4,0).
要注意x、y的取值范围(0≤t≤4,0≤y≤400).
故选:C.
8.解:∵∠C=90°,∠A=30°,BC=4cm,
∴AB=2BC=8cm,
∵点D为AB的中点,
∴CD=4cm,
故选:B.
9.解:∵四边形ABCD是矩形,
∴AO=BO=DO=CO,AC=BD,故①③正确;
∵BO=DO,
∴S△ABO=S△ADO,故②正确;
当∠ABD=45°时,
则∠AOD=90°,
∴AC⊥BD,
∴矩形ABCD变成正方形,故⑤正确,
而④不一定正确,矩形的对角线只是相等,
∴正确结论的个数是4个.
故选:C.
10.解:设等腰直角三角形的直角边为a,正方形边长为c,
则S2=(a+c)(a﹣c)=a2﹣c2,
∴S2=S1﹣S3,
∴S3=2S1﹣2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1.
故选:A.
二、细心填一填(本大题共8个小题,每小题3分,共24分)
11.解:由题意得,x+2≥0且x﹣1≠0,
解得x≥﹣2且x≠1.
故答案为:x≥﹣2且x≠1.
12.解:根据题意,知点Q的坐标是(﹣3+2,4﹣3),即(﹣1,1),
故答案为:(﹣1,1).
13.解:设所求的一次函数解析式为y=kx+b,
∵直线y=kx+b与y=2x+3平行,
∴k=2,
∵点P(0,﹣1)在直线y=2x+b上,
∴﹣0+b=﹣1,解得b=﹣1,
∴所求的一次函数解析式为y=2x﹣1.
故答案为y=2x﹣1.
14.解:作AD⊥BC于D,
当AB=AC=10,BC=12时,BD=BC=6,
底边上的高AD==8,
当AB=AC=12,BC=10时,BD=BC=5,
底边上的高AD==,
故答案为:8cm或cm.
15.解:根据平行四边形的性质可知,∠A+∠B=180°,
∵∠A:∠B=2:3,
∴∠A=72°,∠B=108°
∴∠C=72°,∠D=108°.
故答案为72,108.
16.解:∵AE=EB,DE⊥AB,
∴DA=DB,
∴∠B=∠DAE,
∵DE⊥AB,DC⊥AC,DE=DC,
∴∠DAE=∠DAC,
∴∠B=∠BAD=∠CAD=30°,
故答案为30°.
17.解:∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴BC=2EF=2×2=4,
∴菱形ABCD的周长=4BC=4×4=16.
故答案为16.
18.解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
三、用心做一做(本大题共7个小题,共66分,要求写出证明步骤或解答过程)
19.解:(1)点B关于y轴的对称点坐标为(﹣3,2);
(2)如图所示,△A1OB1即为所求;
(3)在(2)的条件下,A1的坐标为(﹣1,﹣3).
故答案为:(1)(﹣3,2);(3)(﹣1,﹣3)
20.解:(1)a=50﹣4﹣6﹣14﹣10=16;
(2)如图所示:
(3)本次测试的优秀率是:×100%=52%.
21.证明:(1)∵∠1=∠2,
∴DE=CE,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
∴Rt△ADE≌Rt△BEC(HL);
(2)∵Rt△ADE≌Rt△BEC,
∴∠3=∠4,
∵∠3+∠5=90°,
∴∠4+∠5=90°,
∴∠DEC=90°,
∴△CDE是直角三角形.
22.证明:∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,∠BAD=∠CAD.
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN.
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°.
∴四边形ADCE为矩形.
23.解:(1)由图可得,
汽车在前9分钟内的平均速度是:12÷9=km/min;
(2)由图可得,
汽车在中途停了:16﹣9=7min,
即汽车在中途停了7min;
(3)设当16≤t≤30时,S与t的函数关系式是S=at+b,
,得,
即当16≤t≤30时,S与t的函数关系式是S=2t﹣20.
24.解:(1)由题意可得,
w=(12﹣10)x+(23﹣15)(100﹣x)=﹣6x+800
∴w与x之间的函数关系式为w=﹣6x+800;
(2)由题意可得,
﹣6x+800≤40%[10x+15(100﹣x)]
解得:x≥50
又由(1)得:w=﹣6x+800,k=﹣6<0,
∴w随x的增大而减小
∴当x=50时,w达到最大值,即最大利润w=﹣50×6+800=500元,
此时100﹣x=100﹣50=50只
答:购进A型文具50只,B型文具50只时所获利润最大,利润最大为500元.
25.证明:(1)由题意得:AE=2t,CD=4t,
∵DF⊥BC,
∴∠CFD=90°,
∵∠C=30°,
∴DF=CD=×4t=2t,
∴AE=DF;
∵DF⊥BC,
∴∠CFD=∠B=90°,
∴DF∥AE,
∴四边形AEFD是平行四边形.
(2)四边形AEFD能够成为菱形,理由是:
由(1)得:AE=DF,
∵∠DFC=∠B=90°,
∴AE∥DF,
∴四边形AEFD为平行四边形,
若?AEFD为菱形,则AE=AD,
∵AC=100,CD=4t,
∴AD=100﹣4t,
∴2t=100﹣4t,
t=,
∴当t=时,四边形AEFD能够成为菱形;
(3)分三种情况:
①当∠EDF=90°时,如图3,
则四边形DFBE为矩形,
∴DF=BE=2t,
∵AB=AC=50,AE=2t,
∴2t=50﹣2t,
t=,
②当∠DEF=90°时,如图4,
∵四边形AEFD为平行四边形,
∴EF∥AD,
∴∠ADE=∠DEF=90°,
在Rt△ADE中,∠A=60°,AE=2t,
∴AD=t,
∴AC=AD+CD,
则100=t+4t,
t=20,
③当∠DFE=90°不成立;
综上所述:当t为或20时,△DEF为直角三角形.
同课章节目录
