陕西省榆林二中2018-2019学年高二下学期期末考试数学(理)试题 Word版含答案
文档属性
| 名称 | 陕西省榆林二中2018-2019学年高二下学期期末考试数学(理)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 239.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-10 11:21:40 | ||
图片预览




文档简介
榆林市第二中学2018--2019学年第二学期期末考试
高二年级数学(理科)试题
命题人:
时间:120分钟 满分:150分
一、选择题(本大题共12小题,共60分)
复数z=的共轭复数所对应的点位于复平面的( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
若f′(x0)=4,则=( )
A. 2 B. 4 C. D. 8
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
A. 假设三内角都不大于60度 B. 假设三内角都大于60度 C. 假设三内角至多有一个大于60度 D. 假设三内角至多有两个大于60度
设则???????????????????????? (??? )
A. 都大于2 B. 至少有一个大于2 C. 至少有一个不小于2 D. 至少有一个不大于2
若复数z=,其中i为虚数单位,则下列结论正确的是( )
A. z的虚部为-i B. C. z2为纯虚数 D. z的共轭复数为-1-i
在一次连环交通事故中,只有一个人需要负主要责任,但在警察询问时,甲说:“主要责任在乙”;乙说:“丙应负主要责任”;丙说“甲说的对”;丁说:“反正我没有责任”.四人中只有一个人说的是真话,则该事故中需要负主要责任的人是()
A. 甲 B. 乙 C. 丙 D. 丁
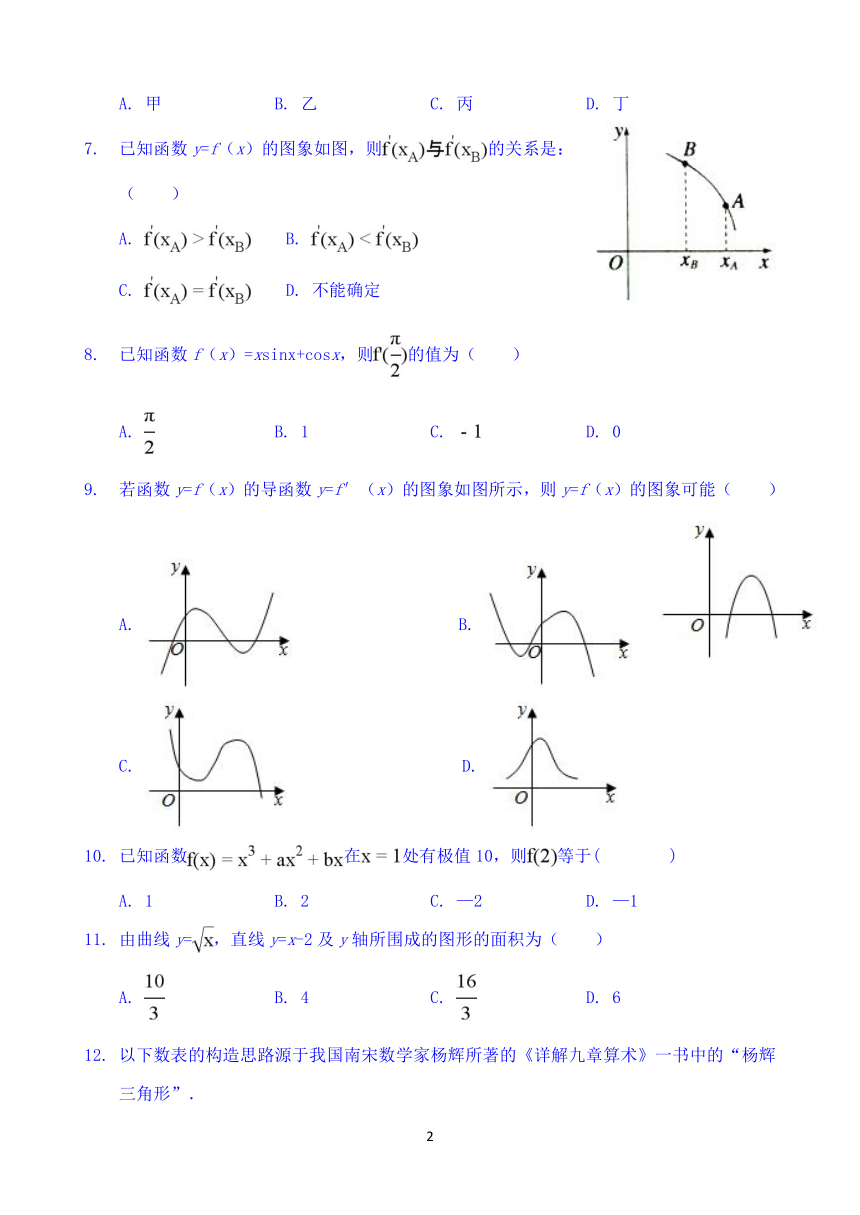
已知函数y=f(x)的图象如图,则的关系是:( )
A. B. C. D. 不能确定
已知函数f(x)=xsinx+cosx,则的值为( )
A. B. 1 C. D. 0
若函数y=f(x)的导函数y=f′(x)的图象如图所示,则y=f(x)的图象可能( )
A. B.
C. D.
已知函数在处有极值10,则等于(? ? ?)
A. 1 B. 2 C. —2 D. —1
由曲线y=,直线y=x-2及y轴所围成的图形的面积为( )
A. B. 4 C. D. 6
以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”. 该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
A. B.
C. D.
二、填空题(本大题共4小题,共20分)
+与2+的大小关系为________.
若直线为曲线的一条切线,则实数的值是________________.
定积分(2x+)dx的值为______ .
如图甲是第七届国际数学教育大会(简称ICME-7)的会徽图案,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图乙中的直角三角形继续作下去,记OA1,OA2,…OAn,…的长度构成数列{an},则此数列的通项公式为an=______.
三、解答题(本大题共6小题,共70分)
(本小题10分)求曲线y=,y=2-x,y=-x所围成图形的面积.
(本小题12分)已知函数,a,若在处与直线相切. 求a,b的值; 求在上的极值.
(本小题12分)已知函数. 当,求函数的图象在点处的切线方程; 当时,求函数的单调区间.
(本小题12分)已知函数在处的切线的斜率为1.
求a的值及f(x)的最大值; 用数学归纳法证明:
(本小题12分)在平面直角坐标系xOy中,直线l的参数方程为(t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=2sinθ. (1)写出直线l的普通方程和圆C的直角坐标方程; (2)若点P坐标为(3,),圆C与直线l交于A、B两点,求|PA|+|PB|的值.
(本小题12分)已知x,y∈R,且x+y=1. (1)求证:x2+3y2≥; (2)当xy>0时,不等式|恒成立,求a的取值范围.
高二理科数学答案
1.C 2.D 3.B 4.C 5.C 6.A 7.B 8.D 9.C 10. B11. C 12.B 13.+>2+? 14.1 15.3+ln2 16.
17. (本小题10分)解:由题意,如图所示:
由y=,y=2-x,y=-x可得交点坐标分别为(1,1),(0,0),(3,-1), 则S= =.
18. (本小题12分)解:(1)f′(x)=-2bx, ∵函数f(x)在x=1处与直线相切, ∴,即,解得; (2)由(1)得:f(x)=lnx-x2,定义域为(0,+∞). f′(x)=-x=, 令f′(x)>0,解得0<x<1,令f′(x)<0,得x>1. ∴f(x)在上单调递增,在(1,e)上单调递减, ∴f(x)在上的极大值为f(1)=-,无极小值.
19. (本小题12分)解:(1)根据题意,当a=2时,, ∴,∴,, ∴函教f(x)的图象在点(1,f(1))处的切线方程为. (2)由题知,函数f(x)的定义域为(0,+∞), ,令,解得x1=1,x2=a-1, ①当a>2时,a-1>1, 在区间(0,1)和(a-1,+∞)上,, 在区间(1,a-1)上,, 故函数f(x)的单调递增区间是(0,1)和(a-1,+∞),单调递减区间是(1,a-1). ②当a =2时,f'(x)0恒成立,故函数f(x)的单调递增区间是(0,+∞). ③当1<a<2时,a-1<1, 在区间(0,a-1)和(1,+∞)上f'(x)>0,在(a-1,1)上f'(x)<0, 故函数f(x)的单调递增区间是(0,a-1)和(1,+∞),单调递减区间是(a-1,1) ④当a =1时,f'(x)=x-1,x>1时f'(x)>0,x<1时f'(x)<0, 函数f(x)的单调递增区间是(1,+∞),单调递减区间是(0,1) ⑤当0<a<1时,, 函数f(x)的单调递增区间是,单调递减区间是(0,1), 综上所述, ?①a>2时函数f(x)的单调递增区间是(0,1)和(a-1,+∞),单调递减区间是(1,a-1); ②a=2时,函数f(x)的单调递增区间是, ③当1<a<2时,函数f(x)的单调递增区间是和,单调递减区间是; ④当时,函数f(x)的单调递增区间是,单调递减区间是.
20. (本小题12分)解:(1)函数f(x)的定义域为(-1,+∞).求导数,得f ′(x)=-a. 由已知,得f ′(-)=1,即-a=1,∴a=1. 此时f(x)=ln(1+x)-x,f ′(x)=-1=, 当-1<x<0时,f ′(x)>0;当x>0时,f ′(x)<0. ∴当x=0时,f(x)取得极大值,该极大值即为最大值, ∴f(x)max=f(0)=0; (2)用数学归纳法证明: ①当n=1时,左边=1=lne,右边=ln2,∴左边>右边,不等式成立. ②假设当n=k时,不等式成立,即1+++…+>ln(k+1).那么1+++…++>ln(k+1)+, 由(1),知x>ln(1+x)(x>-1,且x≠0). 令x=,则>ln(1+)=ln, ∴ln(k+1)+>ln(k+1)+ln=ln(k+2), ∴1+++…++>ln(k+2).即当n=k+1时,不等式也成立. 根据①②,可知不等式对任意n∈N*都成立.
21. (本小题12分)解:(1)由,得直线l的普通方程为x+y-3-=0, 又由ρ=2sinθ,得圆C的直角坐标方程为x2+y2-2y=0, 即x2+(y-)2=5; (2)把直线l的参数方程代入圆C的直角坐标方程, 得2+2=5, 即t2-3t+4=0. 由于Δ=(3)2-4×4=2>0, 故可设t1、t2是上述方程的两实数根, 所以t1+t2=3,t1·t2=4. 又直线l过点P(3, ),A、B两点对应的参数分别为t1、t2, 所以|PA|+|PB|=|t1|+|t2|=t1+t2=3.
22. (本小题12分)解:(1)由柯西不等式得[x2+(][12+()2]. ∴(x2+3y2)×≥(x+y)2,当且仅当x=3y时取等号. ∴x2+3y2≥; (2)=(x+y)()=2+, 要使得不等式|恒成立,即可转化为|a-2|+|a+1|≤4, 当a≥2时,2a-1≤4,可得2, 当-1<a<2时,3≤4,可得-1<a<2, 当a≤-1时,-2a+1≤4,可得, ∴a的取值范围为:( -].
高二年级数学(理科)试题
命题人:
时间:120分钟 满分:150分
一、选择题(本大题共12小题,共60分)
复数z=的共轭复数所对应的点位于复平面的( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
若f′(x0)=4,则=( )
A. 2 B. 4 C. D. 8
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
A. 假设三内角都不大于60度 B. 假设三内角都大于60度 C. 假设三内角至多有一个大于60度 D. 假设三内角至多有两个大于60度
设则???????????????????????? (??? )
A. 都大于2 B. 至少有一个大于2 C. 至少有一个不小于2 D. 至少有一个不大于2
若复数z=,其中i为虚数单位,则下列结论正确的是( )
A. z的虚部为-i B. C. z2为纯虚数 D. z的共轭复数为-1-i
在一次连环交通事故中,只有一个人需要负主要责任,但在警察询问时,甲说:“主要责任在乙”;乙说:“丙应负主要责任”;丙说“甲说的对”;丁说:“反正我没有责任”.四人中只有一个人说的是真话,则该事故中需要负主要责任的人是()
A. 甲 B. 乙 C. 丙 D. 丁
已知函数y=f(x)的图象如图,则的关系是:( )
A. B. C. D. 不能确定
已知函数f(x)=xsinx+cosx,则的值为( )
A. B. 1 C. D. 0
若函数y=f(x)的导函数y=f′(x)的图象如图所示,则y=f(x)的图象可能( )
A. B.
C. D.
已知函数在处有极值10,则等于(? ? ?)
A. 1 B. 2 C. —2 D. —1
由曲线y=,直线y=x-2及y轴所围成的图形的面积为( )
A. B. 4 C. D. 6
以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”. 该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
A. B.
C. D.
二、填空题(本大题共4小题,共20分)
+与2+的大小关系为________.
若直线为曲线的一条切线,则实数的值是________________.
定积分(2x+)dx的值为______ .
如图甲是第七届国际数学教育大会(简称ICME-7)的会徽图案,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图乙中的直角三角形继续作下去,记OA1,OA2,…OAn,…的长度构成数列{an},则此数列的通项公式为an=______.
三、解答题(本大题共6小题,共70分)
(本小题10分)求曲线y=,y=2-x,y=-x所围成图形的面积.
(本小题12分)已知函数,a,若在处与直线相切. 求a,b的值; 求在上的极值.
(本小题12分)已知函数. 当,求函数的图象在点处的切线方程; 当时,求函数的单调区间.
(本小题12分)已知函数在处的切线的斜率为1.
求a的值及f(x)的最大值; 用数学归纳法证明:
(本小题12分)在平面直角坐标系xOy中,直线l的参数方程为(t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=2sinθ. (1)写出直线l的普通方程和圆C的直角坐标方程; (2)若点P坐标为(3,),圆C与直线l交于A、B两点,求|PA|+|PB|的值.
(本小题12分)已知x,y∈R,且x+y=1. (1)求证:x2+3y2≥; (2)当xy>0时,不等式|恒成立,求a的取值范围.
高二理科数学答案
1.C 2.D 3.B 4.C 5.C 6.A 7.B 8.D 9.C 10. B11. C 12.B 13.+>2+? 14.1 15.3+ln2 16.
17. (本小题10分)解:由题意,如图所示:
由y=,y=2-x,y=-x可得交点坐标分别为(1,1),(0,0),(3,-1), 则S= =.
18. (本小题12分)解:(1)f′(x)=-2bx, ∵函数f(x)在x=1处与直线相切, ∴,即,解得; (2)由(1)得:f(x)=lnx-x2,定义域为(0,+∞). f′(x)=-x=, 令f′(x)>0,解得0<x<1,令f′(x)<0,得x>1. ∴f(x)在上单调递增,在(1,e)上单调递减, ∴f(x)在上的极大值为f(1)=-,无极小值.
19. (本小题12分)解:(1)根据题意,当a=2时,, ∴,∴,, ∴函教f(x)的图象在点(1,f(1))处的切线方程为. (2)由题知,函数f(x)的定义域为(0,+∞), ,令,解得x1=1,x2=a-1, ①当a>2时,a-1>1, 在区间(0,1)和(a-1,+∞)上,, 在区间(1,a-1)上,, 故函数f(x)的单调递增区间是(0,1)和(a-1,+∞),单调递减区间是(1,a-1). ②当a =2时,f'(x)0恒成立,故函数f(x)的单调递增区间是(0,+∞). ③当1<a<2时,a-1<1, 在区间(0,a-1)和(1,+∞)上f'(x)>0,在(a-1,1)上f'(x)<0, 故函数f(x)的单调递增区间是(0,a-1)和(1,+∞),单调递减区间是(a-1,1) ④当a =1时,f'(x)=x-1,x>1时f'(x)>0,x<1时f'(x)<0, 函数f(x)的单调递增区间是(1,+∞),单调递减区间是(0,1) ⑤当0<a<1时,, 函数f(x)的单调递增区间是,单调递减区间是(0,1), 综上所述, ?①a>2时函数f(x)的单调递增区间是(0,1)和(a-1,+∞),单调递减区间是(1,a-1); ②a=2时,函数f(x)的单调递增区间是, ③当1<a<2时,函数f(x)的单调递增区间是和,单调递减区间是; ④当时,函数f(x)的单调递增区间是,单调递减区间是.
20. (本小题12分)解:(1)函数f(x)的定义域为(-1,+∞).求导数,得f ′(x)=-a. 由已知,得f ′(-)=1,即-a=1,∴a=1. 此时f(x)=ln(1+x)-x,f ′(x)=-1=, 当-1<x<0时,f ′(x)>0;当x>0时,f ′(x)<0. ∴当x=0时,f(x)取得极大值,该极大值即为最大值, ∴f(x)max=f(0)=0; (2)用数学归纳法证明: ①当n=1时,左边=1=lne,右边=ln2,∴左边>右边,不等式成立. ②假设当n=k时,不等式成立,即1+++…+>ln(k+1).那么1+++…++>ln(k+1)+, 由(1),知x>ln(1+x)(x>-1,且x≠0). 令x=,则>ln(1+)=ln, ∴ln(k+1)+>ln(k+1)+ln=ln(k+2), ∴1+++…++>ln(k+2).即当n=k+1时,不等式也成立. 根据①②,可知不等式对任意n∈N*都成立.
21. (本小题12分)解:(1)由,得直线l的普通方程为x+y-3-=0, 又由ρ=2sinθ,得圆C的直角坐标方程为x2+y2-2y=0, 即x2+(y-)2=5; (2)把直线l的参数方程代入圆C的直角坐标方程, 得2+2=5, 即t2-3t+4=0. 由于Δ=(3)2-4×4=2>0, 故可设t1、t2是上述方程的两实数根, 所以t1+t2=3,t1·t2=4. 又直线l过点P(3, ),A、B两点对应的参数分别为t1、t2, 所以|PA|+|PB|=|t1|+|t2|=t1+t2=3.
22. (本小题12分)解:(1)由柯西不等式得[x2+(][12+()2]. ∴(x2+3y2)×≥(x+y)2,当且仅当x=3y时取等号. ∴x2+3y2≥; (2)=(x+y)()=2+, 要使得不等式|恒成立,即可转化为|a-2|+|a+1|≤4, 当a≥2时,2a-1≤4,可得2, 当-1<a<2时,3≤4,可得-1<a<2, 当a≤-1时,-2a+1≤4,可得, ∴a的取值范围为:( -].
同课章节目录
