人教版七年级下册9.3 一元一次不等式组课件(45张PPT)
文档属性
| 名称 | 人教版七年级下册9.3 一元一次不等式组课件(45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-10 00:00:00 | ||
图片预览








文档简介
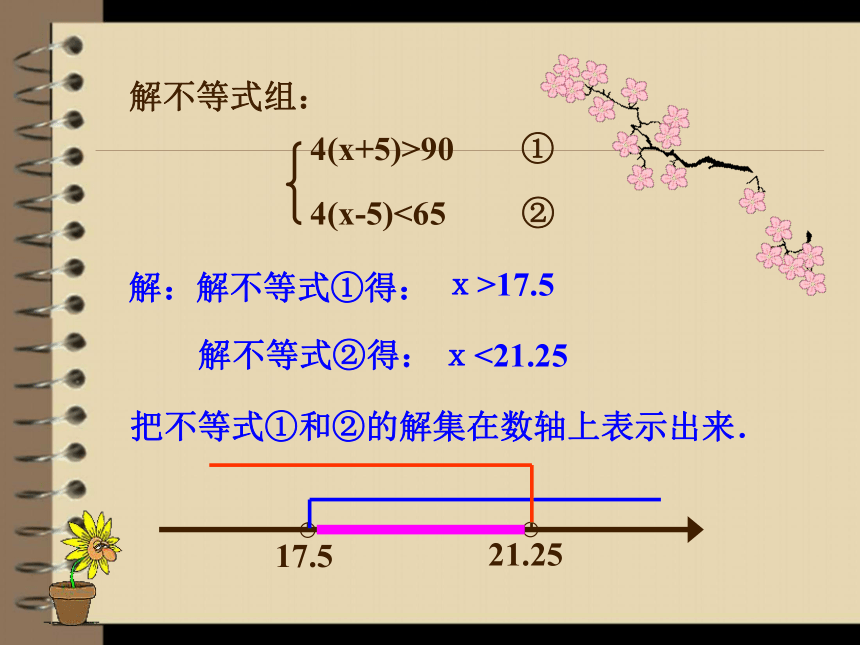
课件45张PPT。 某校冬季烧煤取暖时间为4个月.如果每个月比计划多烧5吨煤, 那么取暖用煤总量将超过90吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足65吨,试问该校计划每月烧煤多少吨?解:设该校计划每月烧煤x吨,根据题意,得且 4(x-5)<65 ②4(x+5)>90 ① 未知数x同时满足① ②两个条件,把① ②两个不等式合在一起得: 一元一次不等式组:把两个不等式合起来,就组成一个一元一次不等式组. 1.知道一元一次不等式组及其解集的含义;知道什么叫解不等式组;
2.理解一元一次不等式组的解集是这个不等式组的解集的公共部分,如果各个不等式的解集没有公共部分,那么这个不等式无解;
3.说出解一元一次不等式组的两个步 骤;
4.会利用数轴解一元一次不等式组,初步领会数形结合的思想.知识与能力 1.通过求不等式组的解集,体验“求同存异”的处理问题的思路;
2.会利用数轴,求出一元一次不等式组的解集,培养数形结合意识.过程与方法 懂得一元一次不等式组解集的含义,初步渗透交集思想.情感态度与价值观 1.理解有关不等式组的概念;
2.会解由两个一元一次不等式组成的不等式组;
3.掌握一元一次不等式组的解法步骤并准确地求出解集;
4.会利用数轴求出一元一次不等式组的解集. 重点 1.利用数轴确定不等式组的解集;
2.正确应用不等式的基本性质对不等式进行变形、求不等式组中各个不等式解集的公共部分;
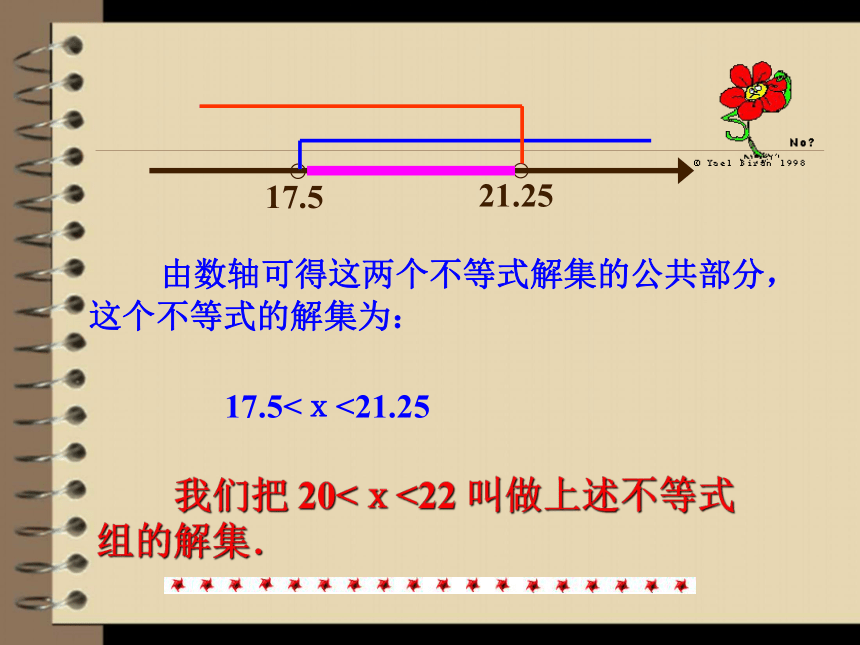
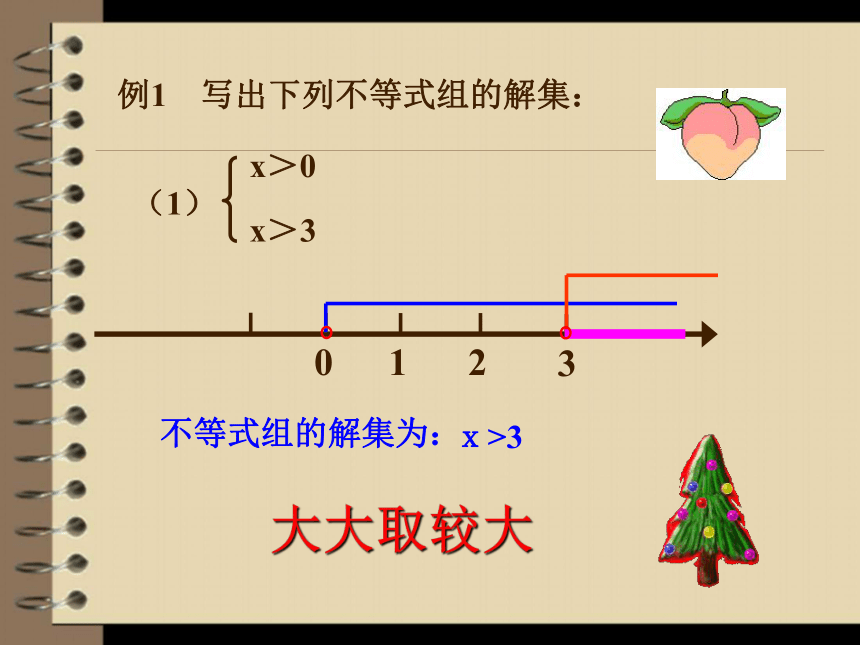
3.理解一元一次不等式组解集的含义.难点判断下列哪些是一元一次不等式组? √××√解:解不等式①得: x>17.5解不等式②得: x<21.25 把不等式①和②的解集在数轴上表示出来.解不等式组: 由数轴可得这两个不等式解集的公共部分,这个不等式的解集为: 17.5<x<21.25 我们把 20<x<22 叫做上述不等式组的解集. 不等式组中所有不等式的解集的公共部分叫做不等式组的解集. 求不等式组解集的过程叫做解不等式组.知识要点不等式组的解集为: x>3大大取较大例1 写出下列不等式组的解集:不等式组的解集为: x<0小小取较小不等式组的解集为:0<x< 3大大小小大中间找不等式组的解集为空集.即:不等式组无解小小大大解不了一般由两个一元一次不等式组成的不等式组由四种基本类型确定,它们的解集、数轴表示如下表:(设a1.解:不等式组的解集是 x≤-2.解:不等式组无解.解一元一次不等式组的方法: 2.(1)利用数轴找几个解集的公共部分;(2)利用规律:大大取较大,小小取较小;
大小小大中间找,小小大大解不了.1.求出不等式组中各个不等式的解集.3.写出这个不等式组的解集;解:解不等式①得: x< 1解不等式②得: x≤2把不等式①和②的解在数轴上表示出来.所以不等式组的解集为: x< 1.解:解不等式① ,得 解不等式② ,得x < 2x >1 所以,原不等式的解集是:1 < x<2 .把不等式①和②的解在数轴上表示出来.解:解不等式①,得x>6解不等式②,得x>5不等式组的解集是:x>6.把不等式①和②的解在数轴上表示出来.解:解不等式① ,得 解不等式② ,得x <-7x >-5 所以,原不等式组无解.把不等式①和②的解在数轴上表示出来.解:解不等式①,得 x < 5
解不等式②,得 x <4
解不等式③,得 x ≤2 把不等式①、②、③的解集表示在同一数轴上,如下图所以,不等式组的解集是x ≤ 2.解:解不等式① ,得 解不等式② ,得x ≥-5所以,不等式的整数解为-5,-4,-3. 例9 当 x 取哪些整数时,不等式 2(x+3)2x 同时成立?解:由不等式2(x+3)2x, 得所以这两个不等式解集的公共部分是:所以当x为 3 时,两个不等式同时成立.x<4x>22 x=16
答:每个小组原先每天生产16件产品.由不等式①得由不等式②得因此,不等式组的解集为 例12 一群女生住若干间宿舍,每间住4人,剩15人无房住;每间住6人,有一间宿舍住不满.问: 解:(1)设有x间宿舍,请写出x应满足的不等式组;7.5第一种,有8间宿舍,
第二种,有9间宿舍,
第三种,有10间宿舍,47名学生;51名学生;55名学生. 例13【2005·咸宁】为了解决学生的饮水问题,学校为各班购置了饮水机,并提供“七里山牌”和“九宫山牌”两种桶装矿泉水,让学生喝上了矿泉水.下表是这两种桶装矿泉水的容积和单价. (1)已知二(1)班五月份饮用两种矿泉水共60桶,饮水费用为292元,问该班五月份饮用两种矿泉水各多少桶?
(2)由于气温升高,估计二(1)班六月份饮水量比五月份增加150L到200L,在饮用两种矿泉水仍为60桶的情况下,设六月份饮用“七里山牌”矿泉水m桶,饮水量为QL,所需饮水费为W元.
①请分别写出Q与m,W与m之间的函数关系式;
②试求六月份该班所需饮水费的范围. 解(1)设饮用“七里山牌”矿泉水 x 桶,则饮用“九宫山牌”矿泉水(60-x)桶,
依题意,得
5.6x+4.5(60-x) =292,
解得x=20,则60-x=40(桶).
答:饮用“七里山牌”矿泉水20桶,饮用“九宫山牌”矿泉水40桶.解(2)①Q=20m+(60-m) ×15=5 m+900,
W=5.6m+(60-m) ×4.5=1.1m+270;
②五月份的饮水量为 20×20+40×15=1000(L).
依题意,六月份的饮水量范围为:
∴ 50≤m≤60,
∵W=1.1m+270,
∴ 1.1×50+270≤W≤1.1×60+270,
解得 325≤W≤336.
答:该班六月份饮水费不少于325元,不超过336元.(1)求出每个不等式的解集;(2)把不等式的解集在同一个数轴上表示出来;(3)找出各个不等式的解集的公共部分;(4)不等式组的解集就是这个公共部分.特别注意,没有公共部分称为不等式组无解.解一元一次不等式组的步骤:1.使不等式x+6≥0与2x-4<0都成立的x的取值范
围是__________.
2.不等式-1≤2x-1≤5的解集是_________.-6≤x<20≤x≤3-2<x<4解:解不等式①,得,
x>2
解不等式②,得,
x>2所以不等式组的解集:x>2.解: 解不等式①,得,
x≥8
解不等式②,得,
x<0所以不等式组无解.4.解下列不等式组-3<m≤-2m≥3a≤-38 解:设有x辆汽车,则有4x+8吨货物,根据题意,可列出不等式9.用若干辆载重量为7吨的汽车运一批货物,若
每辆汽车只装4吨,则剩下8吨货物,若每辆汽
车装满6吨,则最后一辆汽车不满也不空.请
问:有多少辆汽车?解不等式组,得3.5<x<7答:可能有4、5、6辆汽车.10.一次野营活动,小丽把自己带来的若干个香蕉分
给班上若干个同学,如果每人分4个香蕉那么还
剩下20个香蕉,如果每人分8个香蕉,那么最后
一个同学分得的不足8个香蕉,求香蕉的总个
数.解:设共有x名同学,则香蕉有(4x+20)个.不等式组解集为:答:共有44个香蕉.由题意得: 解:设有x间宿舍,则有4x+20人住宿,依题意可得因为宿舍是整数所以
x=6; 4x+20=44答:该班有6间宿舍及44人住宿.11.某班有若干学生住宿,若每间住4人,则有
20人没宿舍住;若每间住8人则有一间没有
住满人,试求该班宿舍间数及住宿人数?
2.理解一元一次不等式组的解集是这个不等式组的解集的公共部分,如果各个不等式的解集没有公共部分,那么这个不等式无解;
3.说出解一元一次不等式组的两个步 骤;
4.会利用数轴解一元一次不等式组,初步领会数形结合的思想.知识与能力 1.通过求不等式组的解集,体验“求同存异”的处理问题的思路;
2.会利用数轴,求出一元一次不等式组的解集,培养数形结合意识.过程与方法 懂得一元一次不等式组解集的含义,初步渗透交集思想.情感态度与价值观 1.理解有关不等式组的概念;
2.会解由两个一元一次不等式组成的不等式组;
3.掌握一元一次不等式组的解法步骤并准确地求出解集;
4.会利用数轴求出一元一次不等式组的解集. 重点 1.利用数轴确定不等式组的解集;
2.正确应用不等式的基本性质对不等式进行变形、求不等式组中各个不等式解集的公共部分;
3.理解一元一次不等式组解集的含义.难点判断下列哪些是一元一次不等式组? √××√解:解不等式①得: x>17.5解不等式②得: x<21.25 把不等式①和②的解集在数轴上表示出来.解不等式组: 由数轴可得这两个不等式解集的公共部分,这个不等式的解集为: 17.5<x<21.25 我们把 20<x<22 叫做上述不等式组的解集. 不等式组中所有不等式的解集的公共部分叫做不等式组的解集. 求不等式组解集的过程叫做解不等式组.知识要点不等式组的解集为: x>3大大取较大例1 写出下列不等式组的解集:不等式组的解集为: x<0小小取较小不等式组的解集为:0<x< 3大大小小大中间找不等式组的解集为空集.即:不等式组无解小小大大解不了一般由两个一元一次不等式组成的不等式组由四种基本类型确定,它们的解集、数轴表示如下表:(设a
大小小大中间找,小小大大解不了.1.求出不等式组中各个不等式的解集.3.写出这个不等式组的解集;解:解不等式①得: x< 1解不等式②得: x≤2把不等式①和②的解在数轴上表示出来.所以不等式组的解集为: x< 1.解:解不等式① ,得 解不等式② ,得x < 2x >1 所以,原不等式的解集是:1 < x<2 .把不等式①和②的解在数轴上表示出来.解:解不等式①,得x>6解不等式②,得x>5不等式组的解集是:x>6.把不等式①和②的解在数轴上表示出来.解:解不等式① ,得 解不等式② ,得x <-7x >-5 所以,原不等式组无解.把不等式①和②的解在数轴上表示出来.解:解不等式①,得 x < 5
解不等式②,得 x <4
解不等式③,得 x ≤2 把不等式①、②、③的解集表示在同一数轴上,如下图所以,不等式组的解集是x ≤ 2.解:解不等式① ,得 解不等式② ,得x ≥-5所以,不等式的整数解为-5,-4,-3. 例9 当 x 取哪些整数时,不等式 2(x+3)
答:每个小组原先每天生产16件产品.由不等式①得由不等式②得因此,不等式组的解集为 例12 一群女生住若干间宿舍,每间住4人,剩15人无房住;每间住6人,有一间宿舍住不满.问: 解:(1)设有x间宿舍,请写出x应满足的不等式组;7.5
第二种,有9间宿舍,
第三种,有10间宿舍,47名学生;51名学生;55名学生. 例13【2005·咸宁】为了解决学生的饮水问题,学校为各班购置了饮水机,并提供“七里山牌”和“九宫山牌”两种桶装矿泉水,让学生喝上了矿泉水.下表是这两种桶装矿泉水的容积和单价. (1)已知二(1)班五月份饮用两种矿泉水共60桶,饮水费用为292元,问该班五月份饮用两种矿泉水各多少桶?
(2)由于气温升高,估计二(1)班六月份饮水量比五月份增加150L到200L,在饮用两种矿泉水仍为60桶的情况下,设六月份饮用“七里山牌”矿泉水m桶,饮水量为QL,所需饮水费为W元.
①请分别写出Q与m,W与m之间的函数关系式;
②试求六月份该班所需饮水费的范围. 解(1)设饮用“七里山牌”矿泉水 x 桶,则饮用“九宫山牌”矿泉水(60-x)桶,
依题意,得
5.6x+4.5(60-x) =292,
解得x=20,则60-x=40(桶).
答:饮用“七里山牌”矿泉水20桶,饮用“九宫山牌”矿泉水40桶.解(2)①Q=20m+(60-m) ×15=5 m+900,
W=5.6m+(60-m) ×4.5=1.1m+270;
②五月份的饮水量为 20×20+40×15=1000(L).
依题意,六月份的饮水量范围为:
∴ 50≤m≤60,
∵W=1.1m+270,
∴ 1.1×50+270≤W≤1.1×60+270,
解得 325≤W≤336.
答:该班六月份饮水费不少于325元,不超过336元.(1)求出每个不等式的解集;(2)把不等式的解集在同一个数轴上表示出来;(3)找出各个不等式的解集的公共部分;(4)不等式组的解集就是这个公共部分.特别注意,没有公共部分称为不等式组无解.解一元一次不等式组的步骤:1.使不等式x+6≥0与2x-4<0都成立的x的取值范
围是__________.
2.不等式-1≤2x-1≤5的解集是_________.-6≤x<20≤x≤3-2<x<4解:解不等式①,得,
x>2
解不等式②,得,
x>2所以不等式组的解集:x>2.解: 解不等式①,得,
x≥8
解不等式②,得,
x<0所以不等式组无解.4.解下列不等式组-3<m≤-2m≥3a≤-38 解:设有x辆汽车,则有4x+8吨货物,根据题意,可列出不等式9.用若干辆载重量为7吨的汽车运一批货物,若
每辆汽车只装4吨,则剩下8吨货物,若每辆汽
车装满6吨,则最后一辆汽车不满也不空.请
问:有多少辆汽车?解不等式组,得3.5<x<7答:可能有4、5、6辆汽车.10.一次野营活动,小丽把自己带来的若干个香蕉分
给班上若干个同学,如果每人分4个香蕉那么还
剩下20个香蕉,如果每人分8个香蕉,那么最后
一个同学分得的不足8个香蕉,求香蕉的总个
数.解:设共有x名同学,则香蕉有(4x+20)个.不等式组解集为:答:共有44个香蕉.由题意得: 解:设有x间宿舍,则有4x+20人住宿,依题意可得因为宿舍是整数所以
x=6; 4x+20=44答:该班有6间宿舍及44人住宿.11.某班有若干学生住宿,若每间住4人,则有
20人没宿舍住;若每间住8人则有一间没有
住满人,试求该班宿舍间数及住宿人数?
