2.8.2 有理数的加减混合运算的应用 课件(24张PPT)
文档属性
| 名称 | 2.8.2 有理数的加减混合运算的应用 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 372.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-10 00:00:00 | ||
图片预览







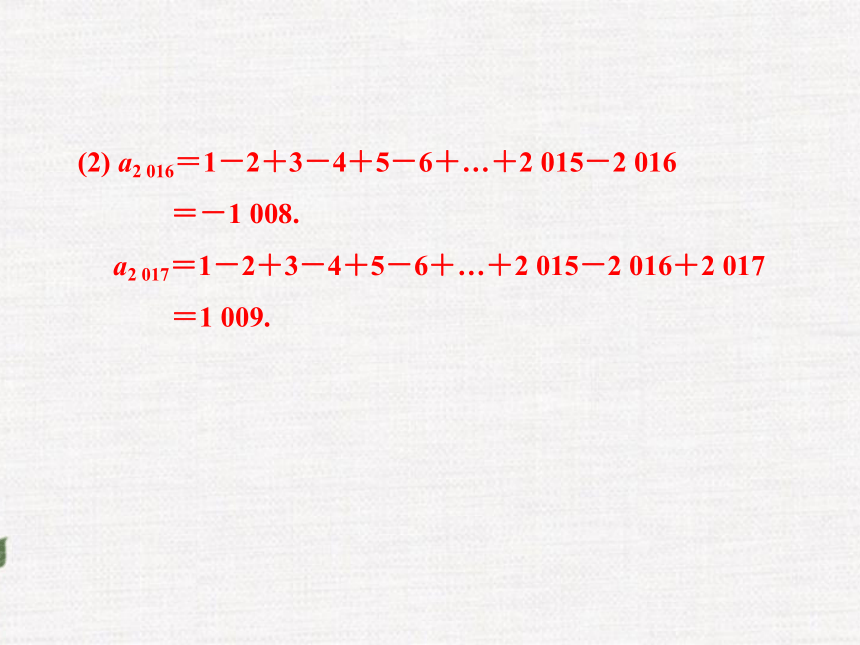

文档简介
课件24张PPT。2.8 有理数的加减混合运算有理数的加减混合运算的应用1题型数学中的应用1.若一个数是-8,另一个数比-8的相反数小3,
则这两个数的和是( )
A.2 B.3 C.-3 D.-19C2.在1,2,3,…,99,100这100个数中,任意加上
“+”或“-”,相加后的结果一定是( )
A.奇数 B.偶数 C.0 D.不确定B 从1到100一共100个数,相邻两个数之和或之差
都为奇数,所以可以得到50个奇数,这50个奇数相
加一定为偶数.3.若 表示运算x+z-(y+w),则 的结
果是 ( )
A.5 B.7 C.9 D.11C 因为 表示运算x+z-(y+w),所以
可表示为3-1-(-2-5)=3-1+7=9.4.有若干个数,第一个记为a1,第二个记为a2,第
三个记为a3,…,第n个记为an,且a1=1,a2=1
-2,a3=1-2+3,a4=1-2+3-4,….
(1)写出a5,a6,a7,a8,并计算结果;
(2)根据以上结果直接写出a2 016,a2 017的结果.
解:(1) a5=1-2+3-4+5=3.
a6=1-2+3-4+5-6=-3.
a7=1-2+3-4+5-6+7=4.
a8=1-2+3-4+5-6+7-8=-4.(2) a2 016=1-2+3-4+5-6+…+2 015-2 016
=-1 008.
a2 017=1-2+3-4+5-6+…+2 015-2 016+2 017
=1 009.
5.问题:能否将1,2,3,4,…,10这10个数分成
两组并分别求和,且使所求的两个和的差为5?
解:1+2+3+…+10=55,要满足题设要求,需
将这10个数分成两组,一组的和为30,另一组的
和为25,然后把它们相减.
下面给出一种分法,例如:
(6+7+8+9)-(1+2+3+4+5+10)=5.
应用:在1,2,3,4,5,6,7,8,9,10这10个数前面任意添上“+”或“-”.
(1)能否使它们的和等于-7?
(2)能否使它们的和等于-2?若能,给出一种添加符
号的方法;若不能,请说明理由.(1)能使它们的和等于-7.如:
(+1)+(-2)+(+3)+(-4)+(+5)+(-6)+(+7)
+(+8)+(-9)+(-10)=1-2+3-4+5-6+7+8
-9-10=-7.(答案不唯一)
(2)不能.因为从1到10一共10个数,相邻两个数之和
或之差都为奇数,所以可以得到5个奇数,这5个
奇数相加一定为奇数,所以无论怎样添加符号,
其和不可能为偶数,当然就不会等于-2.解:2题型实际中的应用6.粮库3天内进出粮食的记录如下(进库的吨数记为正数,
出库的吨数记为负数):+26,-32,-25,+34,-
38,+10.
(1)经过这3天,库里的粮食是增多了还是减少了?并求
出变化的吨数.
(2)经过这3天,仓库管理员结算发现库存粮食有480吨,
那么3天前库存是多少?
(3)若进出的装卸费都是5元/吨,求这3天的装卸费.(+26)+(-32)+(-25)+(+34)+(-38)+(+10)
=26-32-25+34-38+10=-25(吨),
即粮库里的粮食减少了,减少了25吨.
(2) 480-(-25)=480+25=505(吨),
即3天前粮库里存粮505吨.
(3) (26+32+25+34+38+10)×5=825(元),
即这3天的装卸费是825元.解:7.某检修小组从A地出发,在东西方向的马路上检修
线路,如果规定向东行驶为正,向西行驶为负,一
天中七次行驶记录如下(单位:千米):(1)求收工时检修小组距A地多远;
因为(-3)+8+(-9)+10+4+(-6)+(-2)
=-3+8-9+10+4-6-2=2(千米),
所以收工时检修小组距A地2千米.解:(2)在第________次记录时检修小组距A地最远;
由题意得,该小组第一次距A地|-3|=3(千米);第二次距A
地|-3+8|=5(千米);第三次距A地|-3+8-9|=4(千米);
第四次距A地|-3+8-9+10|=6(千米);第五次距A地|-3
+8-9+10+4|=10(千米);第六次距A地|-3+8-9+10
+4-6|=4(千米);第七次距A地|-3+8-9+10+4-6-2|
=2(千米).综上可知,在第五次记录时检修小组距A地最远.
(3)若每千米耗油0.3升,每升汽油需7.2元,则检修小
组工作一天需汽油费多少元?
(3)所求汽油费为(3+8+9+10+4+6+2)×0.3×7.2
=42×0.3×7.2=90.72(元).
五点拨:8.一只蚂蚁在一条直线上运送食物,它先向前爬了
1 m,然后向后爬2 m,再向前爬3 m,然后向后爬
4 m,…,以此规律继续爬行,试探索向前向后往
返的次数a与它的位置关系.解:设向前为正,1+(-2)=3+(-4)=5+(-6)=…
=-1 m,显然每次往返都要后退1 m,
所以往返a次则向后退a m.
点拨:规定向前为正,则向后为负.9.一位股民上周星期五买进某公司股票1 000股,每股
17元,下表为本周内每日该股票收盘时与前一天相
比的涨跌情况(单位:元):注:正号表示比前一天上涨,负号表示比前一天下跌.
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?(1)星期三收盘时,每股价格为
17+(+0.4)+(+0.45)+(-0.1)=17.75(元).
(2)本周内每股最高价是
17+(+0.4)+(+0.45)=17.85(元),
最低价是17+(+0.4)+(+0.45)+(-0.1)+
(-0.25)+(-0.6)=16.9(元).解:10. 小亮用50元钱买了10支钢笔,准备以一定的价格出
售,如果每支钢笔的售价以6元为标准,超过的记作
正数,不足的记作负数,记录如下(单位:元):0.5,
0.7,-1,-1.5,0.8,1,-1.5,-2,1.9,0.9.
(1)这10支钢笔最高的售价和最低的售价各是多少元?
(2)当小亮卖完钢笔后是盈还是亏?解:(1) 6+1.9=7.9(元);6-2=4(元).
所以最高售价是7.9元,最低售价是4元.
(2) 0.5+0.7-1-1.5+0.8+1-1.5-2+1.9+0.9
=-0.2(元),
6×10-0.2-50=9.8(元),
所以当小亮卖完钢笔后是盈利.
11. 已知贵阳市阿哈湖水库正常水位是20米,下表是该
水库今年某周的水位记录情注:高于正常水位记作正,低于正常水位记作负.
(1)本周星期二的水位是________米;
(2)最高水位是________米,最低水位是________米;
(3)请用折线统计图表示本周的水位情况.2022.517(3) 如图所示.解:12.甲、乙两队进行拔河比赛,标志物先向乙队方向移
动0.2 m,又向甲队方向移动0.5 m.相持一会儿后,
又向乙队方向移动0.4 m,随后再向甲队方向移动
1.3 m,在大家的欢呼鼓励声中,标志物又向甲队移
动0.9 m,若规定标志物向某队方向移动2 m,该队
即可获胜,那么现在谁赢了?用算式表示出你的判
断.解:假设标志物向乙队方向移动为正,向甲队方向移
动为负,根据题意可得式子如下:
0.2-0.5+0.4-1.3-0.9
=(0.2+0.4)+(-0.5-1.3-0.9)
=0.6+(-2.7)=-2.1(m).
∴标志物最后向甲队方向移动了2.1 m,2.1 m>2 m,
∴甲队获胜.
点拨:本题也可以取标志物向甲队方向移动为正.
则这两个数的和是( )
A.2 B.3 C.-3 D.-19C2.在1,2,3,…,99,100这100个数中,任意加上
“+”或“-”,相加后的结果一定是( )
A.奇数 B.偶数 C.0 D.不确定B 从1到100一共100个数,相邻两个数之和或之差
都为奇数,所以可以得到50个奇数,这50个奇数相
加一定为偶数.3.若 表示运算x+z-(y+w),则 的结
果是 ( )
A.5 B.7 C.9 D.11C 因为 表示运算x+z-(y+w),所以
可表示为3-1-(-2-5)=3-1+7=9.4.有若干个数,第一个记为a1,第二个记为a2,第
三个记为a3,…,第n个记为an,且a1=1,a2=1
-2,a3=1-2+3,a4=1-2+3-4,….
(1)写出a5,a6,a7,a8,并计算结果;
(2)根据以上结果直接写出a2 016,a2 017的结果.
解:(1) a5=1-2+3-4+5=3.
a6=1-2+3-4+5-6=-3.
a7=1-2+3-4+5-6+7=4.
a8=1-2+3-4+5-6+7-8=-4.(2) a2 016=1-2+3-4+5-6+…+2 015-2 016
=-1 008.
a2 017=1-2+3-4+5-6+…+2 015-2 016+2 017
=1 009.
5.问题:能否将1,2,3,4,…,10这10个数分成
两组并分别求和,且使所求的两个和的差为5?
解:1+2+3+…+10=55,要满足题设要求,需
将这10个数分成两组,一组的和为30,另一组的
和为25,然后把它们相减.
下面给出一种分法,例如:
(6+7+8+9)-(1+2+3+4+5+10)=5.
应用:在1,2,3,4,5,6,7,8,9,10这10个数前面任意添上“+”或“-”.
(1)能否使它们的和等于-7?
(2)能否使它们的和等于-2?若能,给出一种添加符
号的方法;若不能,请说明理由.(1)能使它们的和等于-7.如:
(+1)+(-2)+(+3)+(-4)+(+5)+(-6)+(+7)
+(+8)+(-9)+(-10)=1-2+3-4+5-6+7+8
-9-10=-7.(答案不唯一)
(2)不能.因为从1到10一共10个数,相邻两个数之和
或之差都为奇数,所以可以得到5个奇数,这5个
奇数相加一定为奇数,所以无论怎样添加符号,
其和不可能为偶数,当然就不会等于-2.解:2题型实际中的应用6.粮库3天内进出粮食的记录如下(进库的吨数记为正数,
出库的吨数记为负数):+26,-32,-25,+34,-
38,+10.
(1)经过这3天,库里的粮食是增多了还是减少了?并求
出变化的吨数.
(2)经过这3天,仓库管理员结算发现库存粮食有480吨,
那么3天前库存是多少?
(3)若进出的装卸费都是5元/吨,求这3天的装卸费.(+26)+(-32)+(-25)+(+34)+(-38)+(+10)
=26-32-25+34-38+10=-25(吨),
即粮库里的粮食减少了,减少了25吨.
(2) 480-(-25)=480+25=505(吨),
即3天前粮库里存粮505吨.
(3) (26+32+25+34+38+10)×5=825(元),
即这3天的装卸费是825元.解:7.某检修小组从A地出发,在东西方向的马路上检修
线路,如果规定向东行驶为正,向西行驶为负,一
天中七次行驶记录如下(单位:千米):(1)求收工时检修小组距A地多远;
因为(-3)+8+(-9)+10+4+(-6)+(-2)
=-3+8-9+10+4-6-2=2(千米),
所以收工时检修小组距A地2千米.解:(2)在第________次记录时检修小组距A地最远;
由题意得,该小组第一次距A地|-3|=3(千米);第二次距A
地|-3+8|=5(千米);第三次距A地|-3+8-9|=4(千米);
第四次距A地|-3+8-9+10|=6(千米);第五次距A地|-3
+8-9+10+4|=10(千米);第六次距A地|-3+8-9+10
+4-6|=4(千米);第七次距A地|-3+8-9+10+4-6-2|
=2(千米).综上可知,在第五次记录时检修小组距A地最远.
(3)若每千米耗油0.3升,每升汽油需7.2元,则检修小
组工作一天需汽油费多少元?
(3)所求汽油费为(3+8+9+10+4+6+2)×0.3×7.2
=42×0.3×7.2=90.72(元).
五点拨:8.一只蚂蚁在一条直线上运送食物,它先向前爬了
1 m,然后向后爬2 m,再向前爬3 m,然后向后爬
4 m,…,以此规律继续爬行,试探索向前向后往
返的次数a与它的位置关系.解:设向前为正,1+(-2)=3+(-4)=5+(-6)=…
=-1 m,显然每次往返都要后退1 m,
所以往返a次则向后退a m.
点拨:规定向前为正,则向后为负.9.一位股民上周星期五买进某公司股票1 000股,每股
17元,下表为本周内每日该股票收盘时与前一天相
比的涨跌情况(单位:元):注:正号表示比前一天上涨,负号表示比前一天下跌.
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?(1)星期三收盘时,每股价格为
17+(+0.4)+(+0.45)+(-0.1)=17.75(元).
(2)本周内每股最高价是
17+(+0.4)+(+0.45)=17.85(元),
最低价是17+(+0.4)+(+0.45)+(-0.1)+
(-0.25)+(-0.6)=16.9(元).解:10. 小亮用50元钱买了10支钢笔,准备以一定的价格出
售,如果每支钢笔的售价以6元为标准,超过的记作
正数,不足的记作负数,记录如下(单位:元):0.5,
0.7,-1,-1.5,0.8,1,-1.5,-2,1.9,0.9.
(1)这10支钢笔最高的售价和最低的售价各是多少元?
(2)当小亮卖完钢笔后是盈还是亏?解:(1) 6+1.9=7.9(元);6-2=4(元).
所以最高售价是7.9元,最低售价是4元.
(2) 0.5+0.7-1-1.5+0.8+1-1.5-2+1.9+0.9
=-0.2(元),
6×10-0.2-50=9.8(元),
所以当小亮卖完钢笔后是盈利.
11. 已知贵阳市阿哈湖水库正常水位是20米,下表是该
水库今年某周的水位记录情注:高于正常水位记作正,低于正常水位记作负.
(1)本周星期二的水位是________米;
(2)最高水位是________米,最低水位是________米;
(3)请用折线统计图表示本周的水位情况.2022.517(3) 如图所示.解:12.甲、乙两队进行拔河比赛,标志物先向乙队方向移
动0.2 m,又向甲队方向移动0.5 m.相持一会儿后,
又向乙队方向移动0.4 m,随后再向甲队方向移动
1.3 m,在大家的欢呼鼓励声中,标志物又向甲队移
动0.9 m,若规定标志物向某队方向移动2 m,该队
即可获胜,那么现在谁赢了?用算式表示出你的判
断.解:假设标志物向乙队方向移动为正,向甲队方向移
动为负,根据题意可得式子如下:
0.2-0.5+0.4-1.3-0.9
=(0.2+0.4)+(-0.5-1.3-0.9)
=0.6+(-2.7)=-2.1(m).
∴标志物最后向甲队方向移动了2.1 m,2.1 m>2 m,
∴甲队获胜.
点拨:本题也可以取标志物向甲队方向移动为正.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
