11.3.2多边形及其内角和(2)——多边形的内角和(同步课件)
文档属性
| 名称 | 11.3.2多边形及其内角和(2)——多边形的内角和(同步课件) |

|
|
| 格式 | zip | ||
| 文件大小 | 463.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-11 09:06:50 | ||
图片预览





文档简介
课件13张PPT。多边形及其内角和——多边形的内角和授课:平方差人教版《数学》 八年级上册[慕联教育同步课程]
课程编号:TS1608010202R81110302LDF
慕课联盟课程开发中心:www.moocun.com学习目标1.探索并证明多边形内角和公式,体会化归思想
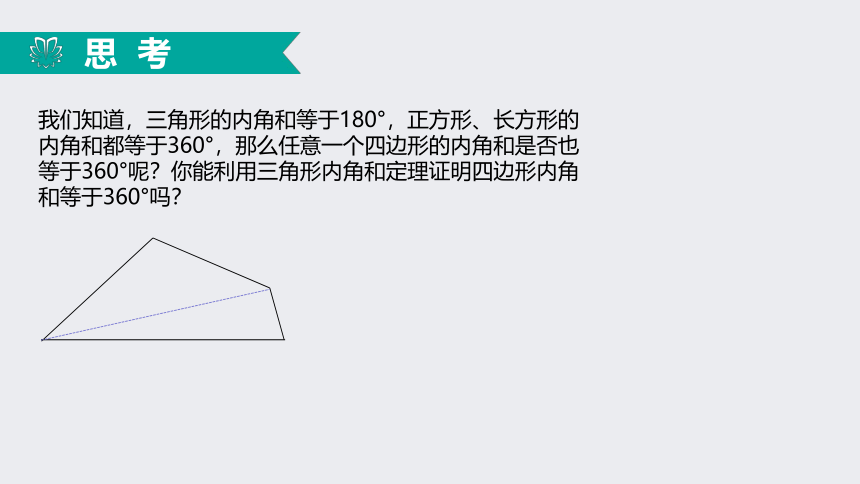
和从具体到抽象的研究问题方法.2.运用多边形内角和公式解决简单问题.3.探索并掌握多边形的外角和公式.思 考我们知道,三角形的内角和等于180°,正方形、长方形的内角和都等于360°,那么任意一个四边形的内角和是否也等于360°呢?你能利用三角形内角和定理证明四边形内角和等于360°吗?思 考如图,四边形ABCD中,连接对角线AC,则四边形ABCD被分为△ABC和△ACD两个三角形.由此可得:∠DAB+∠B+∠BCD+∠D= ∠1+∠2+∠B+∠3+∠4+∠D=(∠1+∠B+∠3)+(∠2+∠4+∠D)∵ ∠1+∠B+∠3=180°∠2+∠4+∠D=180°∴ ∠DAB+∠B+∠BCD+∠D=360°多边形的内角和类比上面的过程,你能推导出五边形和六边形的内角和各是多少吗?观察下图,填空:从五边形的一个顶点出发,可以作( )条对角线,它们将五边形分为( )个三角形,五边形的内角和等于180°×( ).从六边形的一个顶点出发,可以作( )条对角线,它们将六边形分为( )个三角形,六边形的内角和等于180°×( ).233344从以上过程,你能发现多边形的内角和与边数的关系吗?多边形内角和一般地,从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n边形分为(n-2)个三角形,n边形的内角和等于180°×(n-2).这样我们就得出了多边形内角和公式:n边形内角和等于(n-2)×180°.例 题例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:如图,在四边形ABCD中,∠A+∠C=180°.∵ ∠A+∠B+∠C+∠D=(4-2)×180°=360°∴ ∠B+∠D=360°- (∠A+∠C)=360°-180°=180°这就是说,如果四边形的一组对角互补,那么另一组对角也互补.练一练求出下列图形中x的值.例 题例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外交和.六边形的外角和等于多少?思 考如图将例2中六边形换成n边形(n是不小于3的任意整数),可以得到同样的结果吗?n×180°-(n-2)×180°=360°多边形的外角和等于360°练一练(1)一个多边形的各内角都等于120°,它是几边形?(2)一个多边形的内角和等于1260°,它是几边形?知识小结······0n -3 1231234 n -2 ( n -2 )·180o180o360o 540o720o··················慕联提示亲爱的同学,课后请做一个习题测试,假如达到90分以上,就说明你已经很好的掌握了这节课的内容,有关情况将记录在你的学习记录上,亲爱的同学再见!
下节课我们不见不散!
课程编号:TS1608010202R81110302LDF
慕课联盟课程开发中心:www.moocun.com学习目标1.探索并证明多边形内角和公式,体会化归思想
和从具体到抽象的研究问题方法.2.运用多边形内角和公式解决简单问题.3.探索并掌握多边形的外角和公式.思 考我们知道,三角形的内角和等于180°,正方形、长方形的内角和都等于360°,那么任意一个四边形的内角和是否也等于360°呢?你能利用三角形内角和定理证明四边形内角和等于360°吗?思 考如图,四边形ABCD中,连接对角线AC,则四边形ABCD被分为△ABC和△ACD两个三角形.由此可得:∠DAB+∠B+∠BCD+∠D= ∠1+∠2+∠B+∠3+∠4+∠D=(∠1+∠B+∠3)+(∠2+∠4+∠D)∵ ∠1+∠B+∠3=180°∠2+∠4+∠D=180°∴ ∠DAB+∠B+∠BCD+∠D=360°多边形的内角和类比上面的过程,你能推导出五边形和六边形的内角和各是多少吗?观察下图,填空:从五边形的一个顶点出发,可以作( )条对角线,它们将五边形分为( )个三角形,五边形的内角和等于180°×( ).从六边形的一个顶点出发,可以作( )条对角线,它们将六边形分为( )个三角形,六边形的内角和等于180°×( ).233344从以上过程,你能发现多边形的内角和与边数的关系吗?多边形内角和一般地,从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n边形分为(n-2)个三角形,n边形的内角和等于180°×(n-2).这样我们就得出了多边形内角和公式:n边形内角和等于(n-2)×180°.例 题例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:如图,在四边形ABCD中,∠A+∠C=180°.∵ ∠A+∠B+∠C+∠D=(4-2)×180°=360°∴ ∠B+∠D=360°- (∠A+∠C)=360°-180°=180°这就是说,如果四边形的一组对角互补,那么另一组对角也互补.练一练求出下列图形中x的值.例 题例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外交和.六边形的外角和等于多少?思 考如图将例2中六边形换成n边形(n是不小于3的任意整数),可以得到同样的结果吗?n×180°-(n-2)×180°=360°多边形的外角和等于360°练一练(1)一个多边形的各内角都等于120°,它是几边形?(2)一个多边形的内角和等于1260°,它是几边形?知识小结······0n -3 1231234 n -2 ( n -2 )·180o180o360o 540o720o··················慕联提示亲爱的同学,课后请做一个习题测试,假如达到90分以上,就说明你已经很好的掌握了这节课的内容,有关情况将记录在你的学习记录上,亲爱的同学再见!
下节课我们不见不散!
