13.1.2线段垂直平分线的性质(1)垂线定理(同步课件)
文档属性
| 名称 | 13.1.2线段垂直平分线的性质(1)垂线定理(同步课件) |  | |
| 格式 | zip | ||
| 文件大小 | 311.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-11 09:27:43 | ||
图片预览


文档简介
课件11张PPT。授课:大刚老师人教版《数学》 八年级上册13.1.2 线段的垂直平分线的性质(1)
中垂线定理[慕联教育同步课程]
课程编号:TS1703010202R8113010201ZYG
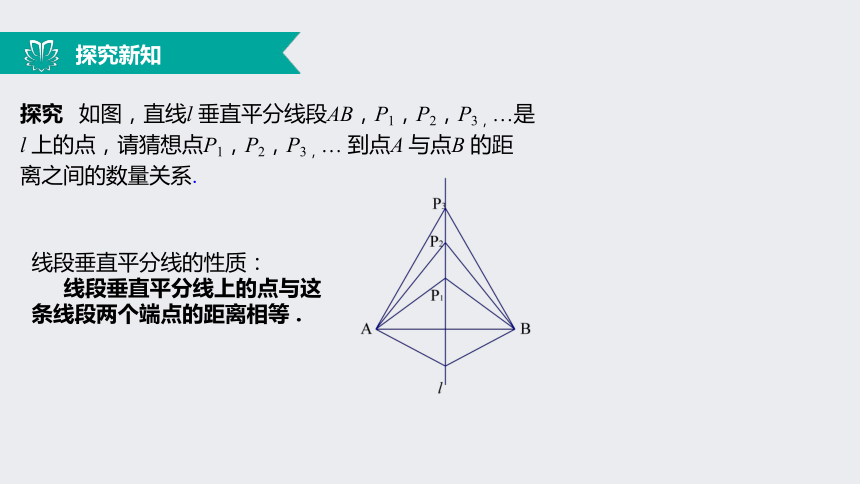
慕课联盟课程开发中心:www.moocun.com学习目标1. 理解线段垂直平分线的性质和判定. 2. 能运用线段垂直平分线的性质和判定解决实际问题.3. 会用尺规经过已知直线外一点作这条直线的垂线,了解作图的道理.探究新知探究 如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
离之间的数量关系.线段垂直平分线的性质:
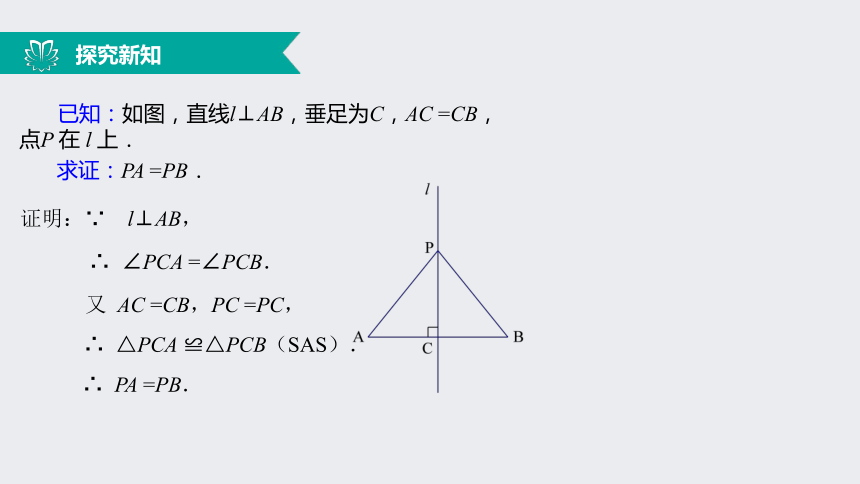
线段垂直平分线上的点与这条线段两个端点的距离相等 . 探究新知 已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在 l 上.
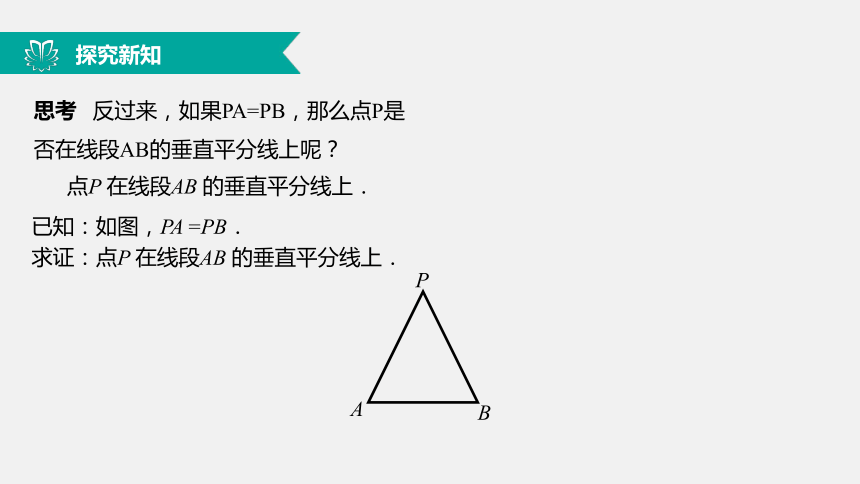
求证:PA =PB. 证明:∵ l⊥AB,∴ ∠PCA =∠PCB.又 AC =CB,PC =PC,∴ △PCA ≌△PCB(SAS).∴ PA =PB.探究新知思考 反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?点P 在线段AB 的垂直平分线上. 已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.PAB 探究新知已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.PAB C 证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上 .
探究新知 线段垂直平分线上的点与这条线段两个端点的距离相等 .
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上 . 应用新知拓展思维练习 如图,AD⊥BC,BD =DC,点C 在AE 的垂
直平分线上,AB,AC,CE 的长度有什么关系?
AB+BD与DE 有什么关系?解: ∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平分线上,
∴ AC =CE.
∴ AB =AC =CE. ∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .知识小结 1.线段垂直平分线上的点与这条线段两个端点的距离相等 . 2. 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上 . 3. 经过已知直线外一点作这条直线的垂线 . 慕联提示亲爱的同学,课后请做一个习题测试,假如达到90分以上,就说明你已经很好的掌握了这节课的内容,有关情况将记录在你的学习记录上,亲爱的同学再见!
下节课我们不见不散!
中垂线定理[慕联教育同步课程]
课程编号:TS1703010202R8113010201ZYG
慕课联盟课程开发中心:www.moocun.com学习目标1. 理解线段垂直平分线的性质和判定. 2. 能运用线段垂直平分线的性质和判定解决实际问题.3. 会用尺规经过已知直线外一点作这条直线的垂线,了解作图的道理.探究新知探究 如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
离之间的数量关系.线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等 . 探究新知 已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在 l 上.
求证:PA =PB. 证明:∵ l⊥AB,∴ ∠PCA =∠PCB.又 AC =CB,PC =PC,∴ △PCA ≌△PCB(SAS).∴ PA =PB.探究新知思考 反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?点P 在线段AB 的垂直平分线上. 已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.PAB 探究新知已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.PAB C 证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上 .
探究新知 线段垂直平分线上的点与这条线段两个端点的距离相等 .
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上 . 应用新知拓展思维练习 如图,AD⊥BC,BD =DC,点C 在AE 的垂
直平分线上,AB,AC,CE 的长度有什么关系?
AB+BD与DE 有什么关系?解: ∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平分线上,
∴ AC =CE.
∴ AB =AC =CE. ∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .知识小结 1.线段垂直平分线上的点与这条线段两个端点的距离相等 . 2. 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上 . 3. 经过已知直线外一点作这条直线的垂线 . 慕联提示亲爱的同学,课后请做一个习题测试,假如达到90分以上,就说明你已经很好的掌握了这节课的内容,有关情况将记录在你的学习记录上,亲爱的同学再见!
下节课我们不见不散!
