第十一章数学活动:镶嵌(同步课件)
图片预览






文档简介
课件14张PPT。授课:平方差人教版《数学》 八年级上册第11章 教学活动[慕联教育同步课程]
课程编号:TS1608010202R81110401LDF
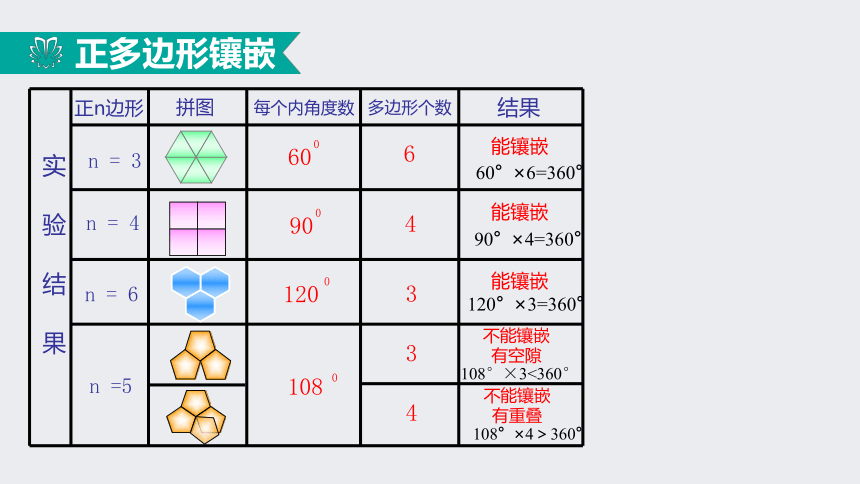
慕课联盟课程开发中心:www.moocun.com—— 平面镶嵌学习目标1.理解平面镶嵌的概念.2.理解多边形能够平面镶嵌的条件;体会从特殊到一般,从简单到复杂的研究问题的思路与方法.3.积极参加数学活动,在数学活动中培养敢于动手,合作交流,归纳反思 .课题导入生活中的各种图案:思 考这些图形拼成一个平面图案的共同特征是什么?(3)铺成的图案把一个平面完全覆盖.(1)用于拼接的图案都是平面图形;(2)拼接处没有空隙,没有重叠的现象;平面镶嵌平面镶嵌的概念:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做多边形覆盖平面(或平面镶嵌).思 考分别剪一些边长相同的正三角形、正方形、正五边形、正六边形,如果用其中一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?正多边形镶嵌64334能镶嵌能镶嵌不能镶嵌
有空隙能镶嵌60° ×6=360° 90° ×4=360° 108°×3<360°108° ×4>360° 120° ×3=360° 不能镶嵌
有重叠实 验 结 果正n边形拼图每个内角度数多边形个数结果 n = 3 n = 4 n =5 n = 6正多边形镶嵌结论:当正多边形的一个内角度数的整数倍是360 ° 时,这种正多边形就能镶嵌.如果选择边长相等的两种正多边形进行镶嵌,你又会选择哪两种呢?正多边形镶嵌两种正多边形拼接在同一点的各个角的和恰好等于360°,这两种正多边形就能镶嵌.图形欣赏正三角形和正方形的平面镶嵌图形欣赏正十二边形与正三角形的平面镶嵌正十边形与正五边形的平面镶嵌正八边形与正方形的平面镶嵌
思 考任意剪出一些形状、大小相同的三角形、四边形,拼拼看,它们能否镶嵌成平面图案.你还可以搜集一些其他用多边形镶嵌的平面图案,或者设计一些地板的平面镶嵌图形,并与你的小伙伴交流一下.知识小结平面镶嵌的概念:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做多边形覆盖平面(或平面镶嵌).当正多边形的一个内角度数的整数倍是360 ° 时,这种正多边形就能镶嵌.慕联提示亲爱的同学,课后请做一个习题测试,假如达到90分以上,就说明你已经很好的掌握了这节课的内容,有关情况将记录在你的学习记录上,亲爱的同学再见!
下节课我们不见不散!
课程编号:TS1608010202R81110401LDF
慕课联盟课程开发中心:www.moocun.com—— 平面镶嵌学习目标1.理解平面镶嵌的概念.2.理解多边形能够平面镶嵌的条件;体会从特殊到一般,从简单到复杂的研究问题的思路与方法.3.积极参加数学活动,在数学活动中培养敢于动手,合作交流,归纳反思 .课题导入生活中的各种图案:思 考这些图形拼成一个平面图案的共同特征是什么?(3)铺成的图案把一个平面完全覆盖.(1)用于拼接的图案都是平面图形;(2)拼接处没有空隙,没有重叠的现象;平面镶嵌平面镶嵌的概念:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做多边形覆盖平面(或平面镶嵌).思 考分别剪一些边长相同的正三角形、正方形、正五边形、正六边形,如果用其中一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?正多边形镶嵌64334能镶嵌能镶嵌不能镶嵌
有空隙能镶嵌60° ×6=360° 90° ×4=360° 108°×3<360°108° ×4>360° 120° ×3=360° 不能镶嵌
有重叠实 验 结 果正n边形拼图每个内角度数多边形个数结果 n = 3 n = 4 n =5 n = 6正多边形镶嵌结论:当正多边形的一个内角度数的整数倍是360 ° 时,这种正多边形就能镶嵌.如果选择边长相等的两种正多边形进行镶嵌,你又会选择哪两种呢?正多边形镶嵌两种正多边形拼接在同一点的各个角的和恰好等于360°,这两种正多边形就能镶嵌.图形欣赏正三角形和正方形的平面镶嵌图形欣赏正十二边形与正三角形的平面镶嵌正十边形与正五边形的平面镶嵌正八边形与正方形的平面镶嵌
思 考任意剪出一些形状、大小相同的三角形、四边形,拼拼看,它们能否镶嵌成平面图案.你还可以搜集一些其他用多边形镶嵌的平面图案,或者设计一些地板的平面镶嵌图形,并与你的小伙伴交流一下.知识小结平面镶嵌的概念:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做多边形覆盖平面(或平面镶嵌).当正多边形的一个内角度数的整数倍是360 ° 时,这种正多边形就能镶嵌.慕联提示亲爱的同学,课后请做一个习题测试,假如达到90分以上,就说明你已经很好的掌握了这节课的内容,有关情况将记录在你的学习记录上,亲爱的同学再见!
下节课我们不见不散!
