上海市金山区2017-2018学年七年级(下)期末数学试卷含解析
文档属性
| 名称 | 上海市金山区2017-2018学年七年级(下)期末数学试卷含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 256.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-10 18:53:39 | ||
图片预览



文档简介
上海市金山区2017-2018学年七年级(下)期末数学试卷
一、选择题(本大题共6题,每题2分,满分12分)
1.下列实数中,是无理数的是( )
A.16 B. C.0. D.
2.下列运算一定正确的是( )
A.=a B.=
C.a2?b2=(a?b)2 D.=a(a≥0)
3.如果三角形的两边长分别是5厘米、7厘米,那么这个三角形第三边的长可能是( )
A.12厘米 B.10厘米 C.2厘米 D.1厘米
4.如图,根据下列条件,不能说明△ABD≌△ACD的是( )
A.BD=DC,AB=AC B.∠ADB=∠ADC,∠BAD=∠CAD
C.∠B=∠C,∠BAD=∠CAD D.∠ADB=∠ADC,AB=AC
5.在平面直角坐标系中,将点P(﹣2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P的坐标是( )
A.(1,5) B.(1,﹣3) C.(﹣5,5) D.(﹣5,﹣3)
6.如图,△ABC≌△AED,点D在BC边上,BC∥AE,∠CAB=80°,则∠BAE的度数是( )
A.35° B.30° C.25° D.20°
二、填空题(本大题共12题,每题2分,满分24分)
7.4的平方根是 .
8.计算:= .
9.比较大小:﹣5 ﹣(填“>”“=”或“<”).
10.用科学记数法表示405500,并保留三个有效数字的近似数表示为 .
11.计算:4×= .
12.在直角坐标平面内,点M(﹣2,3)关于y轴对称的点的坐标是 .
13.若点A(a+1,b)在第二象限,则点B(﹣a,b+1)在 象限.
14.等腰三角形的一边长为2,另一边长为5,则它的周长是 .
15.等腰三角形中,有一个角等于40°,则这个三角形的底角等于 .
16.如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠A=60°,则∠BFC= .
17.如图,已知△ABC是等边三角形,D为BC延长线上一点,CE平分∠ACD,CE=BD,AD=7,那么AE的长度是 .
18.如图,在△ABC中,D是AB上一点,将△BCD沿直线CD翻折,使B点落在AC边所在的直线上的B′处,如果DC=DB′=AB′,则∠B等于 度.
三、简答题(本大题共4题,每题6分,满分24分)
19.计算: +﹣+.
20.计算:4×2÷.
21.计算: +()0﹣()﹣1.
22.利用幂的运算性质计算:2××÷.
四、解答题(本大题共5题,每题8分,满分40分)
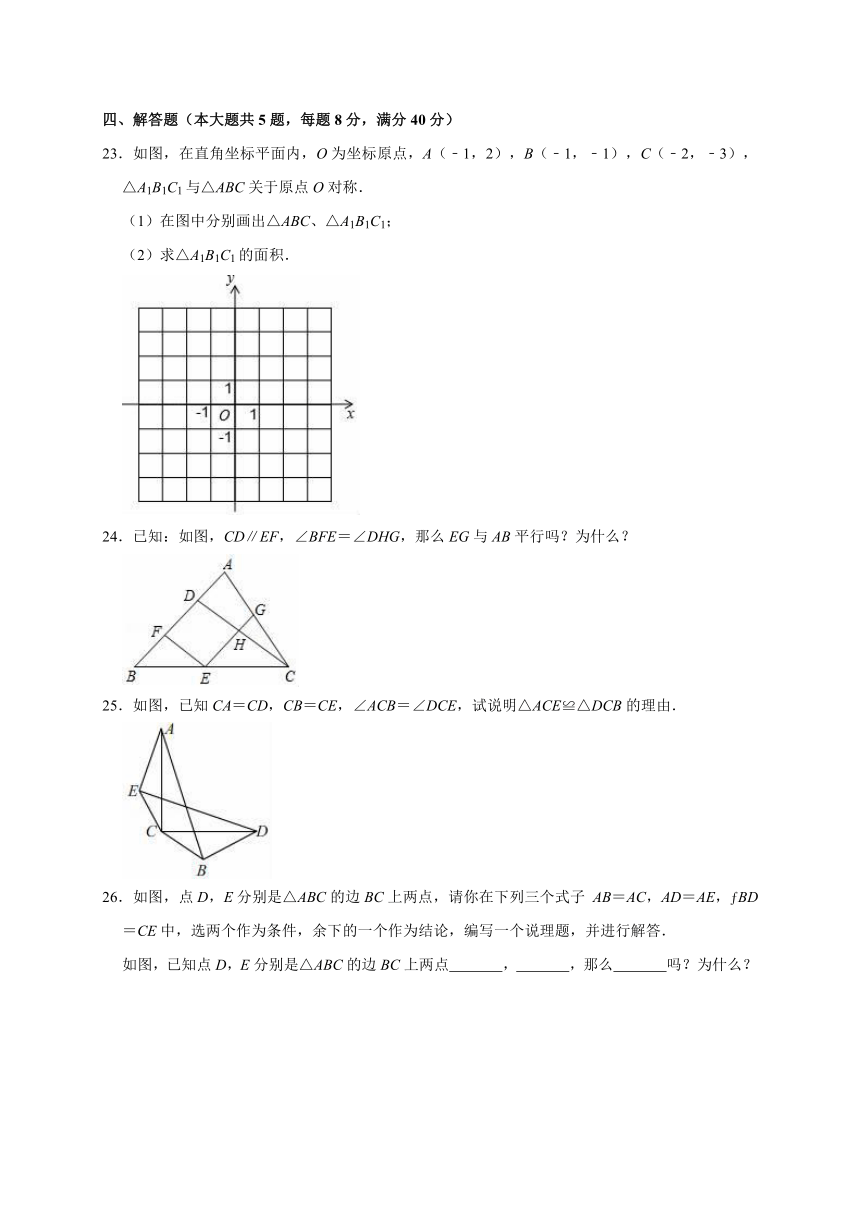
23.如图,在直角坐标平面内,O为坐标原点,A(﹣1,2),B(﹣1,﹣1),C(﹣2,﹣3),△A1B1C1与△ABC关于原点O对称.
(1)在图中分别画出△ABC、△A1B1C1;
(2)求△A1B1C1的面积.
24.已知:如图,CD∥EF,∠BFE=∠DHG,那么EG与AB平行吗?为什么?
25.如图,已知CA=CD,CB=CE,∠ACB=∠DCE,试说明△ACE≌△DCB的理由.
26.如图,点D,E分别是△ABC的边BC上两点,请你在下列三个式子?AB=AC,AD=AE,?BD=CE中,选两个作为条件,余下的一个作为结论,编写一个说理题,并进行解答.
如图,已知点D,E分别是△ABC的边BC上两点 , ,那么 吗?为什么?
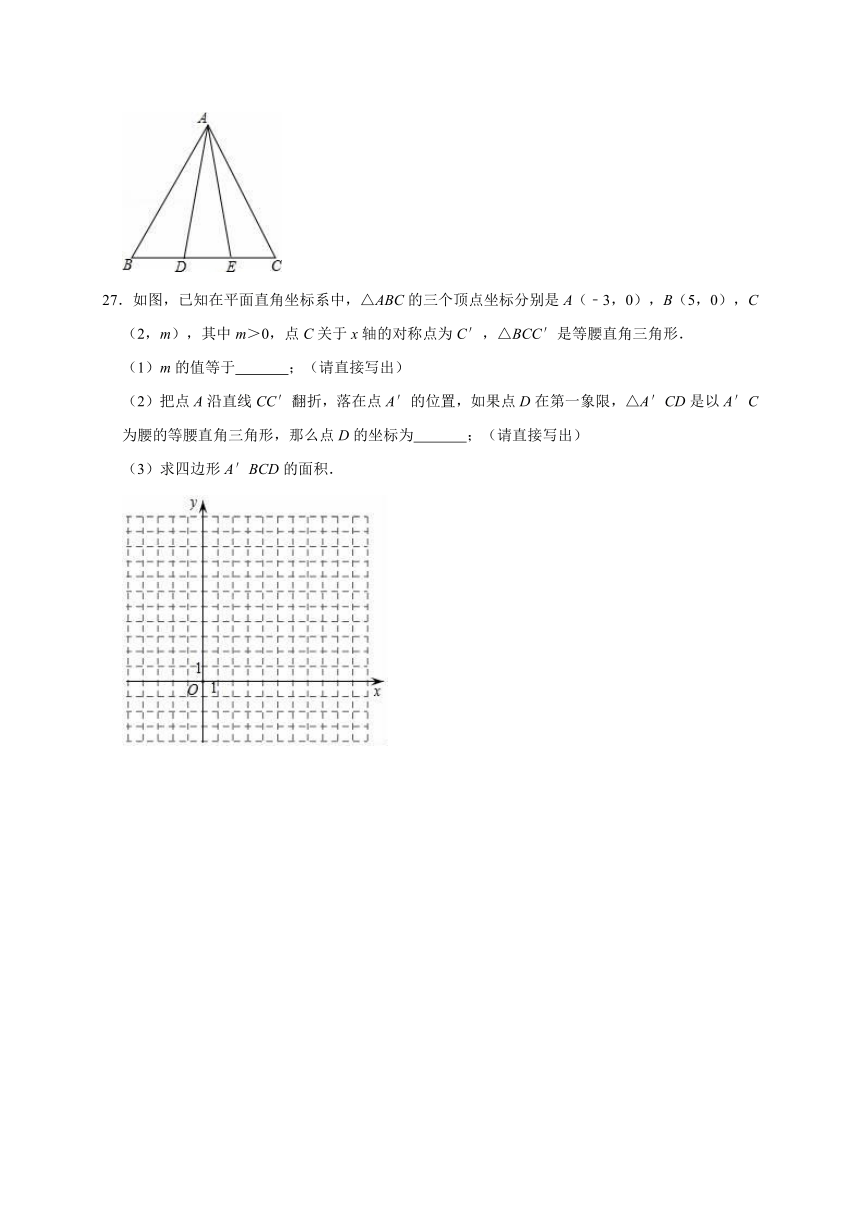
27.如图,已知在平面直角坐标系中,△ABC的三个顶点坐标分别是A(﹣3,0),B(5,0),C(2,m),其中m>0,点C关于x轴的对称点为C′,△BCC′是等腰直角三角形.
(1)m的值等于 ;(请直接写出)
(2)把点A沿直线CC′翻折,落在点A′的位置,如果点D在第一象限,△A′CD是以A′C为腰的等腰直角三角形,那么点D的坐标为 ;(请直接写出)
(3)求四边形A′BCD的面积.
参考答案与试题解析
一、选择题(本大题共6题,每题2分,满分12分)
1.解:无限不循环的小数是无理数,
故选:B.
2.解:A、=|a|,故此选项错误;
B、=,成立,则a,b均为非负数,故此选项错误;
C、a2?b2=(a?b)2,正确;
D、=(a≥0),故此选项错误;
故选:C.
3.解:∵三角形的两边长分别是5厘米、7厘米,
∴设这个三角形第三边长为x,则x的取值范围是:2<x<12,
故这个三角形第三边的长可能是10cm.
故选:B.
4.解:A、由BD=DC、AB=AC,结合AD=AD可得△ACD≌△ABD;
B、由∠ADB=∠ADC,∠BAD=∠CAD,结合AD=AD可得△ACD≌△ABD;
C、由∠B=∠C、∠BAD=∠CAD,结合AD=AD可得△ACD≌△ABD;
D、由∠ADB=∠ADC、AB=AC不能说明△ABD≌△ACD;
故选:D.
5.解:将点P(﹣2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P的坐标是(﹣2+3,1+4),即(1,5),
故选:A.
6.解:∵△ABC≌△AED,
∴∠CAB=∠DAE=80°,
∵BC∥AE,
∴∠CDA=∠DAE=80°
∵AC=AD,
∴∠C=∠ADC=80°,
∴∠CAD=20°,
∵∠CAB=∠DAE,
∴∠CAD=∠BAE=20°
故选:D.
二、填空题(本大题共12题,每题2分,满分24分)
7.解:∵(±2)2=4,
∴4的平方根是±2.
故答案为:±2.
8.解:8==2.
故答案为2.
9.解:(﹣5)2=25,=26,
∵25<26,
∴﹣5>﹣.
故答案为:>.
10.解:405500=4.055×105≈4.05×105.
故答案为:4.06×105.
11.解:原式=×
=2×3
=6,
故答案为:6.
12.解:点M(﹣2,3)关于y轴对称的点的坐标是(2,3),
故答案为:(2,3).
13.解:由A在第二象限可知:a+1<0,b>0,即a<﹣1,b>0,
则可得到:﹣a>1,b+1>1,
故B点在第一象限.
故答案为:第一.
14.解:当2为底时,其它两边都为5,2、5、5可以构成三角形,
周长为12;当2为腰时,其它两边为2和5,∵2+2=4<5,
所以不能构成三角形,故舍去,∴答案只有12.
故填12.
15.解:(1)当40°角本身为底角时,底角就是40°;
(2)当40°角为顶角时,底角=(180°﹣40°)=70°.
∴底角为70°或40°.
故填70°或40°.
16.解:∵∠ABC、∠ACB的平分线BE、CD相交于点F,
∴∠CBF=∠ABC,∠BCF=∠ACB,
∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=120°,
∴∠BFC=180°﹣(∠CBF+BCF)=180°﹣(∠ABC+∠ACB)=120°.
故答案为:120°.
17.解:∵△ABC为等边三角形,
∴AB=AC,∠B=∠ACB=60°,
∴∠ACD=120°,
∵CE平分∠ACD,
∴∠ACE=∠ACD=60°,
在△ABD和△ACE中
,
∴△ABD≌△ACE,
∴AE=AD=7.
故答案为7.
18.解:∵△BCD沿直线CD翻折
∴DB=DB',∠B=∠DB'C
∵AB'=DB'=DC=DB
∴∠A=∠ADB',∠DB'C=∠DCB',∠B=∠DCB
设∠A=x° 则∠ADB'=x
∴∠DB'C=2x=∠DCB'=∠B=∠DCB
根据三角形内角和定理可得:
∴x+2x+4x=180°
x=
∴∠B=2x=
故答案为
三、简答题(本大题共4题,每题6分,满分24分)
19.解:原式=(+1﹣+)
=
20.解:原式=8÷
=8×3
=24.
21.解:原式=﹣1+1﹣+1
=1.
22.解:原式=2××÷==23=8.
四、解答题(本大题共5题,每题8分,满分40分)
23.解:
(1)如图所示:
(2)△A1B1C1的面积=×3×1=.
24.解:平行,
理由:∵CD∥EF,
∴∠BDC=∠BFE,
又∵∠BFE=∠DHG,
∴∠BDC=∠DHG,
∴EG∥AB.
25.解:∵∠ACB=∠DCE,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即:∠ACE=∠DCB,
在△ACE与△DCB中
,
∴△ACE≌△DCB(SAS).
26.解:如图,已知点D,E分别是△ABC的边BC上两点AB=AC,BD=EC,求证:AD=AE
故答案为:AB=AC,BD=EC,AD=AE;
理由:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△ABD与△ACE中
,
∴△ABD≌△ACE(SAS),
∴AD=AE(全等三角形的对应边相等).
27.解:(1)如图,AB与CC'交于E
∵C与C'关于x轴对称
∴BC=BC',BE⊥CC'
∴B是直角顶点,且△BCC'是等腰直角三角形,且BE⊥CC'
∴CE=C'E=BE
∵B(5,0),C(2,m),
∴BE=3=CE
∴m=3
(2)∵点A与点A'关于CC'对称
∴A'(7,0)
∴A'E=5
∵若∠DCA'=90°,且△A'CD是等腰直角三角形
∴DC=DA'
过点D作DF⊥CE于F
∴∠FDC+∠DCF=90°且∠ECA'+DCF=90°
∴∠FDC=∠ECA'且A'C=DC,∠DFC=∠CEA'=90°
∴△DCF=CEA'
∴DF=CE=3,A'E=CF=5
∴EF=8
∴D(5,8)
若∠CA'D=90°,同理可得D(10,5)
∴D(5,8)或(10,5)
(3)∵AE=5,EC=3
∴A'C=
∵SA'BCD=S△A'BC+S△A'CD
∴SA'BCD=×2×3+××=20
一、选择题(本大题共6题,每题2分,满分12分)
1.下列实数中,是无理数的是( )
A.16 B. C.0. D.
2.下列运算一定正确的是( )
A.=a B.=
C.a2?b2=(a?b)2 D.=a(a≥0)
3.如果三角形的两边长分别是5厘米、7厘米,那么这个三角形第三边的长可能是( )
A.12厘米 B.10厘米 C.2厘米 D.1厘米
4.如图,根据下列条件,不能说明△ABD≌△ACD的是( )
A.BD=DC,AB=AC B.∠ADB=∠ADC,∠BAD=∠CAD
C.∠B=∠C,∠BAD=∠CAD D.∠ADB=∠ADC,AB=AC
5.在平面直角坐标系中,将点P(﹣2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P的坐标是( )
A.(1,5) B.(1,﹣3) C.(﹣5,5) D.(﹣5,﹣3)
6.如图,△ABC≌△AED,点D在BC边上,BC∥AE,∠CAB=80°,则∠BAE的度数是( )
A.35° B.30° C.25° D.20°
二、填空题(本大题共12题,每题2分,满分24分)
7.4的平方根是 .
8.计算:= .
9.比较大小:﹣5 ﹣(填“>”“=”或“<”).
10.用科学记数法表示405500,并保留三个有效数字的近似数表示为 .
11.计算:4×= .
12.在直角坐标平面内,点M(﹣2,3)关于y轴对称的点的坐标是 .
13.若点A(a+1,b)在第二象限,则点B(﹣a,b+1)在 象限.
14.等腰三角形的一边长为2,另一边长为5,则它的周长是 .
15.等腰三角形中,有一个角等于40°,则这个三角形的底角等于 .
16.如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠A=60°,则∠BFC= .
17.如图,已知△ABC是等边三角形,D为BC延长线上一点,CE平分∠ACD,CE=BD,AD=7,那么AE的长度是 .
18.如图,在△ABC中,D是AB上一点,将△BCD沿直线CD翻折,使B点落在AC边所在的直线上的B′处,如果DC=DB′=AB′,则∠B等于 度.
三、简答题(本大题共4题,每题6分,满分24分)
19.计算: +﹣+.
20.计算:4×2÷.
21.计算: +()0﹣()﹣1.
22.利用幂的运算性质计算:2××÷.
四、解答题(本大题共5题,每题8分,满分40分)
23.如图,在直角坐标平面内,O为坐标原点,A(﹣1,2),B(﹣1,﹣1),C(﹣2,﹣3),△A1B1C1与△ABC关于原点O对称.
(1)在图中分别画出△ABC、△A1B1C1;
(2)求△A1B1C1的面积.
24.已知:如图,CD∥EF,∠BFE=∠DHG,那么EG与AB平行吗?为什么?
25.如图,已知CA=CD,CB=CE,∠ACB=∠DCE,试说明△ACE≌△DCB的理由.
26.如图,点D,E分别是△ABC的边BC上两点,请你在下列三个式子?AB=AC,AD=AE,?BD=CE中,选两个作为条件,余下的一个作为结论,编写一个说理题,并进行解答.
如图,已知点D,E分别是△ABC的边BC上两点 , ,那么 吗?为什么?
27.如图,已知在平面直角坐标系中,△ABC的三个顶点坐标分别是A(﹣3,0),B(5,0),C(2,m),其中m>0,点C关于x轴的对称点为C′,△BCC′是等腰直角三角形.
(1)m的值等于 ;(请直接写出)
(2)把点A沿直线CC′翻折,落在点A′的位置,如果点D在第一象限,△A′CD是以A′C为腰的等腰直角三角形,那么点D的坐标为 ;(请直接写出)
(3)求四边形A′BCD的面积.
参考答案与试题解析
一、选择题(本大题共6题,每题2分,满分12分)
1.解:无限不循环的小数是无理数,
故选:B.
2.解:A、=|a|,故此选项错误;
B、=,成立,则a,b均为非负数,故此选项错误;
C、a2?b2=(a?b)2,正确;
D、=(a≥0),故此选项错误;
故选:C.
3.解:∵三角形的两边长分别是5厘米、7厘米,
∴设这个三角形第三边长为x,则x的取值范围是:2<x<12,
故这个三角形第三边的长可能是10cm.
故选:B.
4.解:A、由BD=DC、AB=AC,结合AD=AD可得△ACD≌△ABD;
B、由∠ADB=∠ADC,∠BAD=∠CAD,结合AD=AD可得△ACD≌△ABD;
C、由∠B=∠C、∠BAD=∠CAD,结合AD=AD可得△ACD≌△ABD;
D、由∠ADB=∠ADC、AB=AC不能说明△ABD≌△ACD;
故选:D.
5.解:将点P(﹣2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P的坐标是(﹣2+3,1+4),即(1,5),
故选:A.
6.解:∵△ABC≌△AED,
∴∠CAB=∠DAE=80°,
∵BC∥AE,
∴∠CDA=∠DAE=80°
∵AC=AD,
∴∠C=∠ADC=80°,
∴∠CAD=20°,
∵∠CAB=∠DAE,
∴∠CAD=∠BAE=20°
故选:D.
二、填空题(本大题共12题,每题2分,满分24分)
7.解:∵(±2)2=4,
∴4的平方根是±2.
故答案为:±2.
8.解:8==2.
故答案为2.
9.解:(﹣5)2=25,=26,
∵25<26,
∴﹣5>﹣.
故答案为:>.
10.解:405500=4.055×105≈4.05×105.
故答案为:4.06×105.
11.解:原式=×
=2×3
=6,
故答案为:6.
12.解:点M(﹣2,3)关于y轴对称的点的坐标是(2,3),
故答案为:(2,3).
13.解:由A在第二象限可知:a+1<0,b>0,即a<﹣1,b>0,
则可得到:﹣a>1,b+1>1,
故B点在第一象限.
故答案为:第一.
14.解:当2为底时,其它两边都为5,2、5、5可以构成三角形,
周长为12;当2为腰时,其它两边为2和5,∵2+2=4<5,
所以不能构成三角形,故舍去,∴答案只有12.
故填12.
15.解:(1)当40°角本身为底角时,底角就是40°;
(2)当40°角为顶角时,底角=(180°﹣40°)=70°.
∴底角为70°或40°.
故填70°或40°.
16.解:∵∠ABC、∠ACB的平分线BE、CD相交于点F,
∴∠CBF=∠ABC,∠BCF=∠ACB,
∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=120°,
∴∠BFC=180°﹣(∠CBF+BCF)=180°﹣(∠ABC+∠ACB)=120°.
故答案为:120°.
17.解:∵△ABC为等边三角形,
∴AB=AC,∠B=∠ACB=60°,
∴∠ACD=120°,
∵CE平分∠ACD,
∴∠ACE=∠ACD=60°,
在△ABD和△ACE中
,
∴△ABD≌△ACE,
∴AE=AD=7.
故答案为7.
18.解:∵△BCD沿直线CD翻折
∴DB=DB',∠B=∠DB'C
∵AB'=DB'=DC=DB
∴∠A=∠ADB',∠DB'C=∠DCB',∠B=∠DCB
设∠A=x° 则∠ADB'=x
∴∠DB'C=2x=∠DCB'=∠B=∠DCB
根据三角形内角和定理可得:
∴x+2x+4x=180°
x=
∴∠B=2x=
故答案为
三、简答题(本大题共4题,每题6分,满分24分)
19.解:原式=(+1﹣+)
=
20.解:原式=8÷
=8×3
=24.
21.解:原式=﹣1+1﹣+1
=1.
22.解:原式=2××÷==23=8.
四、解答题(本大题共5题,每题8分,满分40分)
23.解:
(1)如图所示:
(2)△A1B1C1的面积=×3×1=.
24.解:平行,
理由:∵CD∥EF,
∴∠BDC=∠BFE,
又∵∠BFE=∠DHG,
∴∠BDC=∠DHG,
∴EG∥AB.
25.解:∵∠ACB=∠DCE,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即:∠ACE=∠DCB,
在△ACE与△DCB中
,
∴△ACE≌△DCB(SAS).
26.解:如图,已知点D,E分别是△ABC的边BC上两点AB=AC,BD=EC,求证:AD=AE
故答案为:AB=AC,BD=EC,AD=AE;
理由:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△ABD与△ACE中
,
∴△ABD≌△ACE(SAS),
∴AD=AE(全等三角形的对应边相等).
27.解:(1)如图,AB与CC'交于E
∵C与C'关于x轴对称
∴BC=BC',BE⊥CC'
∴B是直角顶点,且△BCC'是等腰直角三角形,且BE⊥CC'
∴CE=C'E=BE
∵B(5,0),C(2,m),
∴BE=3=CE
∴m=3
(2)∵点A与点A'关于CC'对称
∴A'(7,0)
∴A'E=5
∵若∠DCA'=90°,且△A'CD是等腰直角三角形
∴DC=DA'
过点D作DF⊥CE于F
∴∠FDC+∠DCF=90°且∠ECA'+DCF=90°
∴∠FDC=∠ECA'且A'C=DC,∠DFC=∠CEA'=90°
∴△DCF=CEA'
∴DF=CE=3,A'E=CF=5
∴EF=8
∴D(5,8)
若∠CA'D=90°,同理可得D(10,5)
∴D(5,8)或(10,5)
(3)∵AE=5,EC=3
∴A'C=
∵SA'BCD=S△A'BC+S△A'CD
∴SA'BCD=×2×3+××=20
同课章节目录
