人教A版数学必修4 1.2.2 同角三角函数的基本关系(共18张ppt)
文档属性
| 名称 | 人教A版数学必修4 1.2.2 同角三角函数的基本关系(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 17.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-11 21:02:00 | ||
图片预览




文档简介
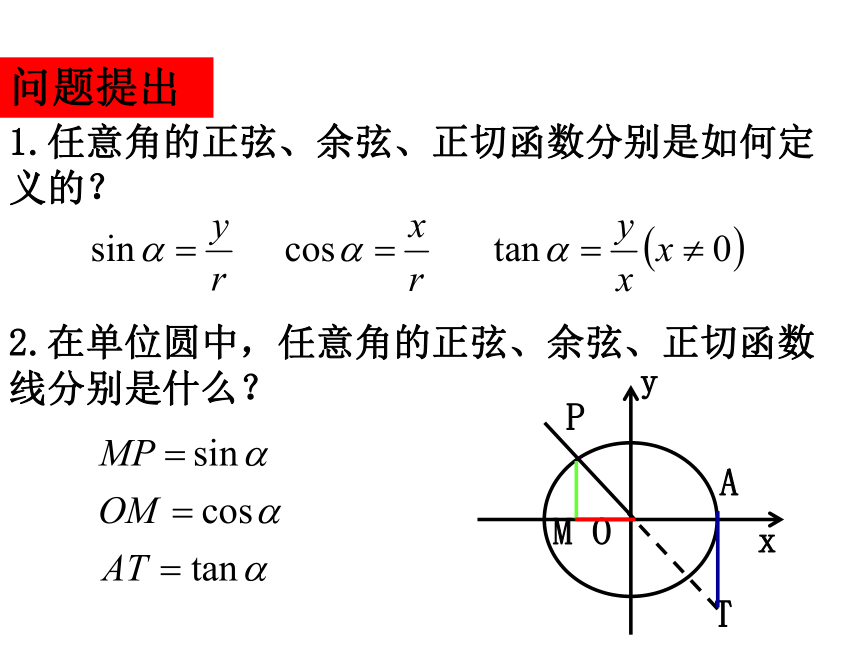
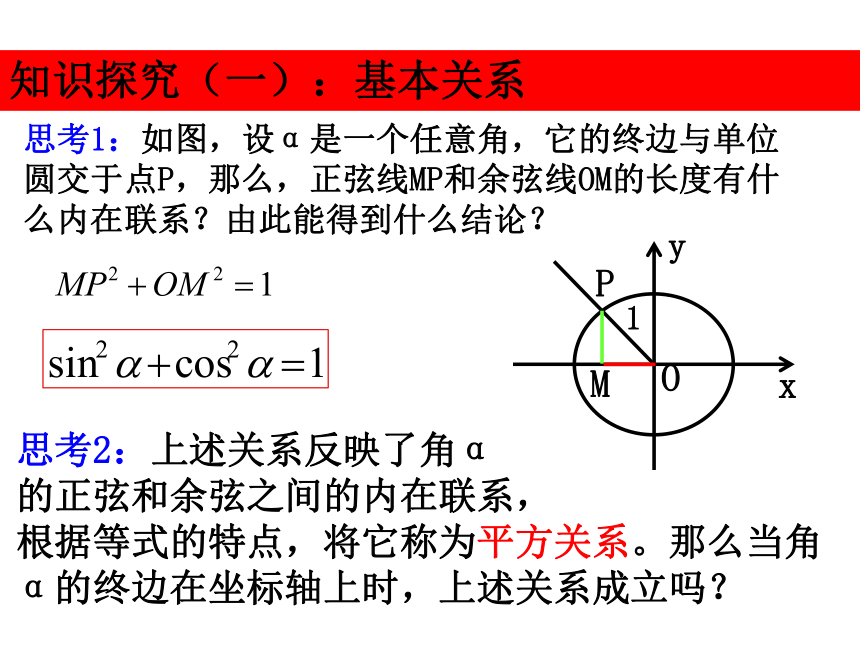
课件18张PPT。任意角的三角函数1.2.2同角三角函数的基本关系问题提出1.任意角的正弦、余弦、正切函数分别是如何定义的?2.在单位圆中,任意角的正弦、余弦、正切函数线分别是什么? 3.对于一个任意角α,sinα,cosα,tanα是三个不同的三角函数,三者之间应存在一定的内在联系,我们希望找出这种同角三角函数之间的基本关系,实现正弦、余弦、正切函数的互相转化,为进一步解决三角恒等变形问题提供理论依据. 知识探究(一):基本关系 思考1:如图,设α是一个任意角,它的终边与单位圆交于点P,那么,正弦线MP和余弦线OM的长度有什么内在联系?由此能得到什么结论? 思考2:上述关系反映了角α
的正弦和余弦之间的内在联系,
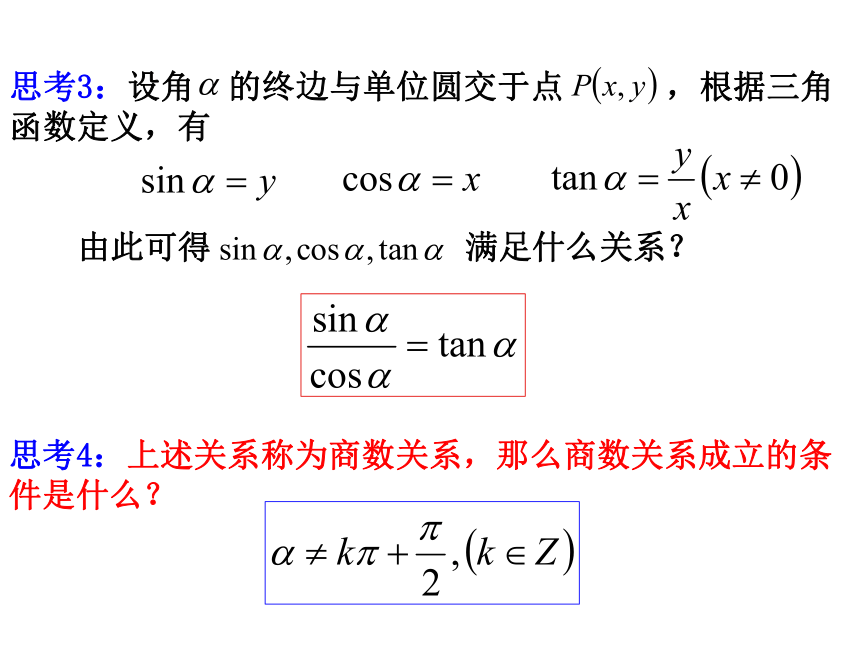
根据等式的特点,将它称为平方关系。那么当角α的终边在坐标轴上时,上述关系成立吗?思考4:上述关系称为商数关系,那么商数关系成立的条件是什么?思考3:设角 的终边与单位圆交于点 ,根据三角函数定义,有
由此可得 满足什么关系?知识探究(二):基本变形 思考1:对于平方关系 可作哪些变形? 思考2:对于商数关系 可作哪些变形?平方和关系与商关系是同角三角函数的两个基本关系,能实现正弦、余弦、正切函数的互相转化,解决三角恒等变形问题。知识探究(三):应用示例 从而解:因为 , 所以 是第三或第四象限角.由 得如果 是第三象限角,那么如果 是第四象限角,那么跟踪练习:(2)解:注意:“1”的灵活代换,特别是关于sina 、cosa齐次式。跟踪练习:例3、求证: 基本思路:由繁到简
可以从左边往右边证,可以从右边往左边证,也可以证明等价式。证明恒等式例3、求证:证明:因此作差法证法二:因为因此由原题知:恒等变形的条件1、求证:sin4α-cos4α=2sin2α-1;证明:
原式左边=(sin2α+cos2α)(sin2α-cos2α)
=sin2α-cos2α
=sin2α-(1-sin2α)
=2sin2α-1=右边.
所以原等式成立.跟踪练习:小结:1.同角三角函数的两个基本关系是对同一个角而言的,由此可以派生出许多变形公式,应用中具有灵活、多变的特点。2.利用平方关系求值时往往要进行开方运算,因此要根据角所在的象限确定三角函数值符号,必要时应就角所在象限进行分类讨论。3.化简、求值、证明,是三角变换的三个基本问题,具有一定的技巧性,需要加强训练,不断总结、提高。课后练习:
的正弦和余弦之间的内在联系,
根据等式的特点,将它称为平方关系。那么当角α的终边在坐标轴上时,上述关系成立吗?思考4:上述关系称为商数关系,那么商数关系成立的条件是什么?思考3:设角 的终边与单位圆交于点 ,根据三角函数定义,有
由此可得 满足什么关系?知识探究(二):基本变形 思考1:对于平方关系 可作哪些变形? 思考2:对于商数关系 可作哪些变形?平方和关系与商关系是同角三角函数的两个基本关系,能实现正弦、余弦、正切函数的互相转化,解决三角恒等变形问题。知识探究(三):应用示例 从而解:因为 , 所以 是第三或第四象限角.由 得如果 是第三象限角,那么如果 是第四象限角,那么跟踪练习:(2)解:注意:“1”的灵活代换,特别是关于sina 、cosa齐次式。跟踪练习:例3、求证: 基本思路:由繁到简
可以从左边往右边证,可以从右边往左边证,也可以证明等价式。证明恒等式例3、求证:证明:因此作差法证法二:因为因此由原题知:恒等变形的条件1、求证:sin4α-cos4α=2sin2α-1;证明:
原式左边=(sin2α+cos2α)(sin2α-cos2α)
=sin2α-cos2α
=sin2α-(1-sin2α)
=2sin2α-1=右边.
所以原等式成立.跟踪练习:小结:1.同角三角函数的两个基本关系是对同一个角而言的,由此可以派生出许多变形公式,应用中具有灵活、多变的特点。2.利用平方关系求值时往往要进行开方运算,因此要根据角所在的象限确定三角函数值符号,必要时应就角所在象限进行分类讨论。3.化简、求值、证明,是三角变换的三个基本问题,具有一定的技巧性,需要加强训练,不断总结、提高。课后练习:
