六年级上册数学导学案 倒数的认识 人教新课标
文档属性
| 名称 | 六年级上册数学导学案 倒数的认识 人教新课标 |

|
|
| 格式 | zip | ||
| 文件大小 | 54.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-11 00:00:00 | ||
图片预览

文档简介
《倒数的认识》学习案
班别:__________ 姓名:__________ 学号:__________
学习目标:
1、通过计算、观察、概括,会说出倒数的意义。
2、能总结出求一个数的倒数的方法,培养抽象思维和归纳能力。
3、会求一个数(分数、整数、小数)的倒数。
学习重点:会说出倒数的意义;求一个数的倒数。
学习难点:会正确地求出一个数的倒数。
一、合作交流:探索倒数的意义。
1、乘积是( )的两个数互为倒数。(请圈出重点词)
2、两个互为倒数的数之间的关系的正确表述。
和互为( ),就是指:的倒数是( ),的倒数是( )。
3、想一想:互为倒数的两个数有什么特点?
(1)互为倒数的两个数的( )是( )。
(2)互为倒数的两个数的分子和分母( )。
(3)如果一个数大于1,那么它的倒数( )1;如果一个数小于1,那么它的倒数( )1。
4、练一练:我是小法官。
(1)结果是1的两个数互为倒数。 ( )
(2)因此,所以的倒数是。 ( )
(3)3和互为倒数,3是倒数,也是倒数。 ( )
(4)互为倒数的两个数的乘积一定是1。 ( )
二、合作探究:研究求一个数的倒数的方法。
1、小组合作学习书本P28例1,并完成下面题目。
例1:下面哪两个数互为倒数?为什么?(用线连一连)
6 1 0
(1)求分数的倒数,只需要交换( )和( )的位置。
(2)求整数的倒数,先把整数看成分母是( )的分数,再交换( )和( )的位置。
(3)1的倒数是( )。0的倒数呢?为什么?
2、练一练:书本P28做一做。
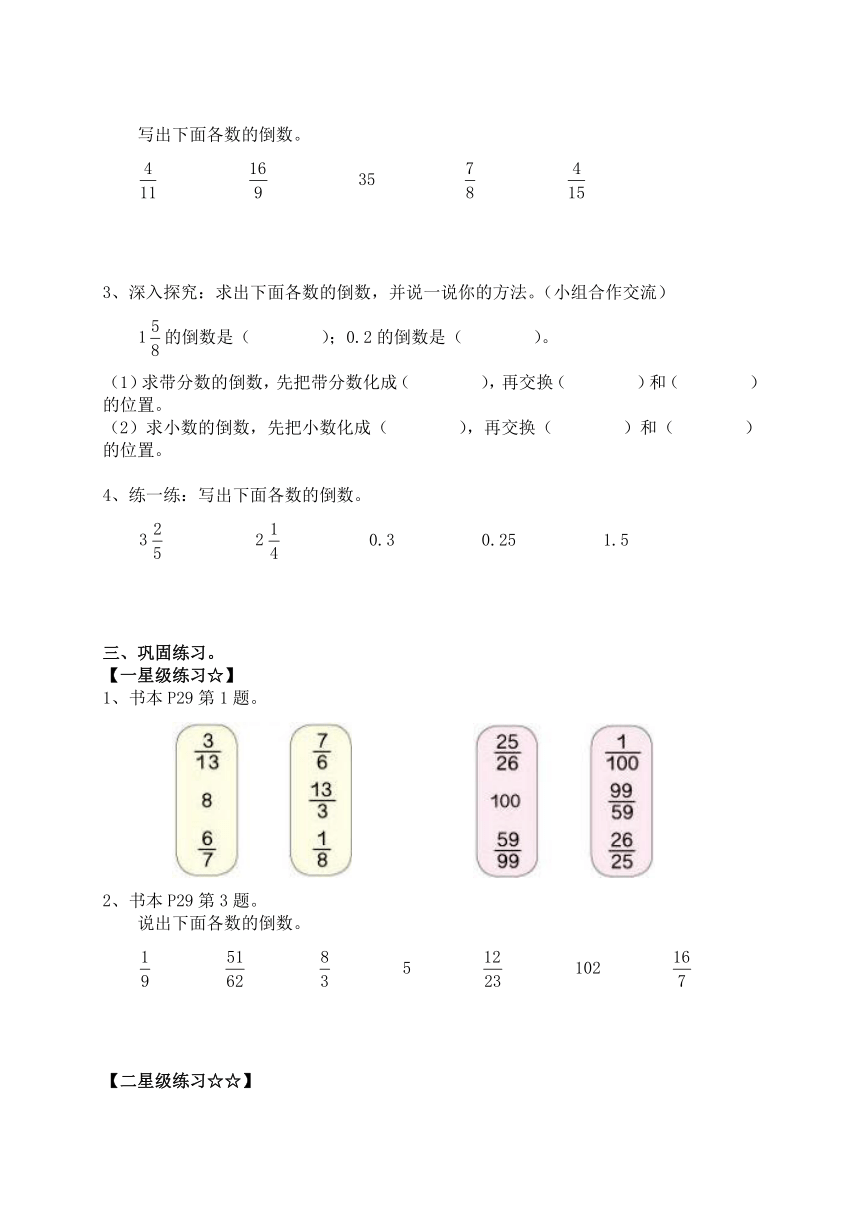
写出下面各数的倒数。
35
3、深入探究:求出下面各数的倒数,并说一说你的方法。(小组合作交流)
的倒数是( );0.2的倒数是( )。
(1)求带分数的倒数,先把带分数化成( ),再交换( )和( )的位置。
(2)求小数的倒数,先把小数化成( ),再交换( )和( )的位置。
4、练一练:写出下面各数的倒数。
0.3 0.25 1.5
三、巩固练习。
【一星级练习☆】
1、书本P29第1题。
2、书本P29第3题。
说出下面各数的倒数。
5 102
【二星级练习☆☆】
1、选一选。
(1)真分数的倒数( )1,假分数的倒数( )1。
A、大于 B、小于 C、等于 D、小于或等于
(2)因为,所以( )。
A、和都是倒数 B、是倒数 C、的倒数是
2、填一填。
(1)( )的倒数是它本身,( )没有倒数。
(2)( )的倒数是;( )与200互为倒数;0.8的倒数是( );与( )互为倒数。
(3)最小合数的倒数是( )。
(4)0.125和它的倒数的乘积是( )。
3、书本P29第2题。
下面的说法对不对?为什么?
(1)与的乘积为1,所以和互为倒数。 ( )
(2),所以、、互为倒数。 ( )
(3)0的倒数还是0。 ( )
(4)一个数的倒数一定比这个数小。 ( )
【三星级练习☆☆☆】
已知(和都不为0),请你比较和的大小。
四、课堂总结。
1、乘积是( )的( )数互为倒数。
2、求分数的倒数,只需要交换( )和( )的位置;求整数(0除外)的倒数,先把整数看成分母是( )的分数,再交换( )和( )的位置;求带分数和小数的倒数,先把带分数化成( ),把小数化成( ),再交换( )和( )的位置。
3、1的倒数是( ),( )没有倒数。
五、课堂检测。
1、填空。
(1)8的倒数是( )。
(2)( )与互为倒数。
(3)与( )的乘积是1。
(4)0.5的倒数是( )。
(5)的倒数是( )。
2、判断。
(1)因为,所以是倒数,也是倒数。 ( )
(2)9的倒数是。 ( )
(3)任何真分数的倒数都是假分数。 ( )
(4)所有的自然数都有倒数。 ( )
班别:__________ 姓名:__________ 学号:__________
学习目标:
1、通过计算、观察、概括,会说出倒数的意义。
2、能总结出求一个数的倒数的方法,培养抽象思维和归纳能力。
3、会求一个数(分数、整数、小数)的倒数。
学习重点:会说出倒数的意义;求一个数的倒数。
学习难点:会正确地求出一个数的倒数。
一、合作交流:探索倒数的意义。
1、乘积是( )的两个数互为倒数。(请圈出重点词)
2、两个互为倒数的数之间的关系的正确表述。
和互为( ),就是指:的倒数是( ),的倒数是( )。
3、想一想:互为倒数的两个数有什么特点?
(1)互为倒数的两个数的( )是( )。
(2)互为倒数的两个数的分子和分母( )。
(3)如果一个数大于1,那么它的倒数( )1;如果一个数小于1,那么它的倒数( )1。
4、练一练:我是小法官。
(1)结果是1的两个数互为倒数。 ( )
(2)因此,所以的倒数是。 ( )
(3)3和互为倒数,3是倒数,也是倒数。 ( )
(4)互为倒数的两个数的乘积一定是1。 ( )
二、合作探究:研究求一个数的倒数的方法。
1、小组合作学习书本P28例1,并完成下面题目。
例1:下面哪两个数互为倒数?为什么?(用线连一连)
6 1 0
(1)求分数的倒数,只需要交换( )和( )的位置。
(2)求整数的倒数,先把整数看成分母是( )的分数,再交换( )和( )的位置。
(3)1的倒数是( )。0的倒数呢?为什么?
2、练一练:书本P28做一做。
写出下面各数的倒数。
35
3、深入探究:求出下面各数的倒数,并说一说你的方法。(小组合作交流)
的倒数是( );0.2的倒数是( )。
(1)求带分数的倒数,先把带分数化成( ),再交换( )和( )的位置。
(2)求小数的倒数,先把小数化成( ),再交换( )和( )的位置。
4、练一练:写出下面各数的倒数。
0.3 0.25 1.5
三、巩固练习。
【一星级练习☆】
1、书本P29第1题。
2、书本P29第3题。
说出下面各数的倒数。
5 102
【二星级练习☆☆】
1、选一选。
(1)真分数的倒数( )1,假分数的倒数( )1。
A、大于 B、小于 C、等于 D、小于或等于
(2)因为,所以( )。
A、和都是倒数 B、是倒数 C、的倒数是
2、填一填。
(1)( )的倒数是它本身,( )没有倒数。
(2)( )的倒数是;( )与200互为倒数;0.8的倒数是( );与( )互为倒数。
(3)最小合数的倒数是( )。
(4)0.125和它的倒数的乘积是( )。
3、书本P29第2题。
下面的说法对不对?为什么?
(1)与的乘积为1,所以和互为倒数。 ( )
(2),所以、、互为倒数。 ( )
(3)0的倒数还是0。 ( )
(4)一个数的倒数一定比这个数小。 ( )
【三星级练习☆☆☆】
已知(和都不为0),请你比较和的大小。
四、课堂总结。
1、乘积是( )的( )数互为倒数。
2、求分数的倒数,只需要交换( )和( )的位置;求整数(0除外)的倒数,先把整数看成分母是( )的分数,再交换( )和( )的位置;求带分数和小数的倒数,先把带分数化成( ),把小数化成( ),再交换( )和( )的位置。
3、1的倒数是( ),( )没有倒数。
五、课堂检测。
1、填空。
(1)8的倒数是( )。
(2)( )与互为倒数。
(3)与( )的乘积是1。
(4)0.5的倒数是( )。
(5)的倒数是( )。
2、判断。
(1)因为,所以是倒数,也是倒数。 ( )
(2)9的倒数是。 ( )
(3)任何真分数的倒数都是假分数。 ( )
(4)所有的自然数都有倒数。 ( )
