4.2.2 由视图到立体图形 教案(表格式)
文档属性
| 名称 | 4.2.2 由视图到立体图形 教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-11 00:00:00 | ||
图片预览

文档简介
4.2 立体图形的视图
2.由视图到立体图形
课题
2.由视图到立体图形
授课人
教
学
目
标
知识技能
会根据立体图形的三视图描述出实际的立体图形.
数学思考
通过本节课的学习,让学生通过感知、观察、实验、操作等数学活动充分感受数学在实际生活中的运用.
问题解决
尝试从不同角度寻求解决问题的方法,通过对解决问题过程的反思,获得解决问题的经验.
情感态度
在学习与探讨的过程中体验数学问题的探索性与创造性.通过学生之间的交流与合作,培养学生在独立思考问题的基础上能够聆听与理解他人的意见,并学会与他人合作,在合作中体验成功的喜悦,建立自信心.
教学
重点
会通过立体图形的三视图描述出实际的立体图形.
教学
难点
通过立体图形的三视图描述由一些几何体组合的立体图形.
授课
类型
新授课
课时
教具
多媒体
教学活动
教学
步骤
师生活动
设计意图
回顾
【知识回顾】
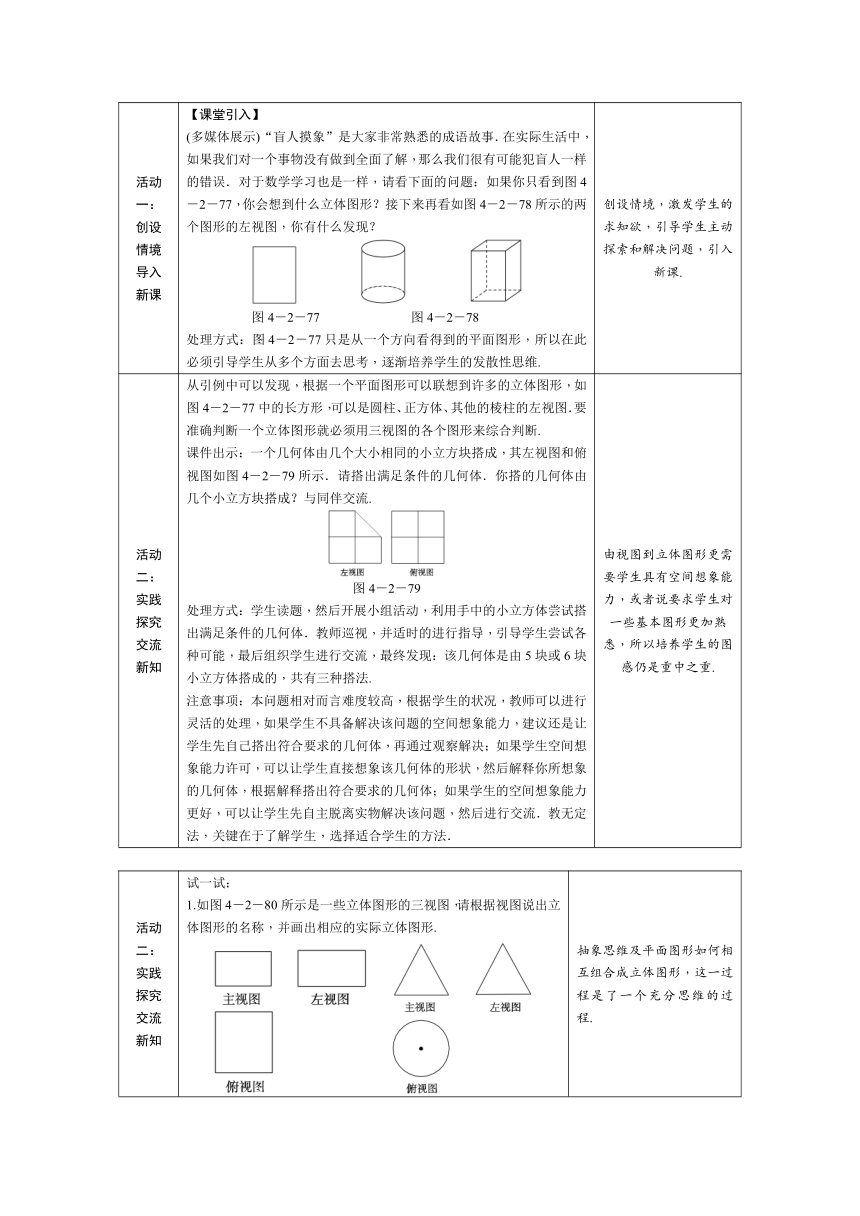
试画出粉笔的三视图(如图).
图4-2-76
复习前面所学习的立体图形的三视图的画法,为进入新课的做好准备.
活动
一:
创设
情境
导入
新课
【课堂引入】
(多媒体展示)“盲人摸象”是大家非常熟悉的成语故事.在实际生活中,如果我们对一个事物没有做到全面了解,那么我们很有可能犯盲人一样的错误.对于数学学习也是一样,请看下面的问题:如果你只看到图4-2-77,你会想到什么立体图形?接下来再看如图4-2-78所示的两个图形的左视图,你有什么发现?
图4-2-77 图4-2-78
处理方式:图4-2-77只是从一个方向看得到的平面图形,所以在此必须引导学生从多个方面去思考,逐渐培养学生的发散性思维.
创设情境,激发学生的求知欲,引导学生主动探索和解决问题,引入新课.
活动
二:
实践
探究
交流
新知
从引例中可以发现,根据一个平面图形可以联想到许多的立体图形,如图4-2-77中的长方形,可以是圆柱、正方体、其他的棱柱的左视图.要准确判断一个立体图形就必须用三视图的各个图形来综合判断.
课件出示:一个几何体由几个大小相同的小立方块搭成,其左视图和俯视图如图4-2-79所示.请搭出满足条件的几何体.你搭的几何体由几个小立方块搭成?与同伴交流.
图4-2-79
处理方式:学生读题,然后开展小组活动,利用手中的小立方体尝试搭出满足条件的几何体.教师巡视,并适时的进行指导,引导学生尝试各种可能,最后组织学生进行交流,最终发现:该几何体是由5块或6块小立方体搭成的,共有三种搭法.
注意事项:本问题相对而言难度较高,根据学生的状况,教师可以进行灵活的处理,如果学生不具备解决该问题的空间想象能力,建议还是让学生先自己搭出符合要求的几何体,再通过观察解决;如果学生空间想象能力许可,可以让学生直接想象该几何体的形状,然后解释你所想象的几何体,根据解释搭出符合要求的几何体;如果学生的空间想象能力更好,可以让学生先自主脱离实物解决该问题,然后进行交流.教无定法,关键在于了解学生,选择适合学生的方法.
由视图到立体图形更需要学生具有空间想象能力,或者说要求学生对一些基本图形更加熟悉,所以培养学生的图感仍是重中之重.
活动
二:
实践
探究
交流
新知
试一试:
1.如图4-2-80所示是一些立体图形的三视图,请根据视图说出立体图形的名称,并画出相应的实际立体图形.
(1) (2)
图4-2-80
2.如图4-2-81是一个物体的三视图,试说出该物体的形状.
图4-2-81
抽象思维及平面图形如何相互组合成立体图形,这一过程是了一个充分思维的过程.
活动
三:
开放
训练
体现
应用
【应用举例】
例1 (教材P127例3)图4-2-82所示的是一些立体图形的三视图,请根据视图说出立体图形的名称.
(1)
(2)
图4-2-82
学以致用,感受不同的方向观察几何体的不同性.已知部分形状图及有关数据信息,反向思考几何体的构成,从而力图让学生逐步脱离实物观察,迫使学生进入真正的想象层面,提高空间想象能力.
【拓展提升】
例2 如图4-2-83所示是由几个大小相同的立方块所搭几何体的俯视图,小正方形中的数字表示在该位置上小立方块的个数.请画出相应的几何体的主视图和左视图.
图4-2-83
在此过程中,通过由问题到模型,由模型再到脱离模型,较为完整地反映出一个问题解决的全貌.
活动
三:
开放
训练
体现
应用
【达标测评】
1.如图4-2-84所示的是某几何体的三视图,则该几何体的形状是( )
A.长方体 B.三棱柱 C.圆锥 D.正方体
图4-2-84 图4-2-85
2.由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上小正方体的个数,那么该几何体的左视图是( )
A B C D
图4-2-86
3.一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )
图4-2-87
A.6 B.8 C.12 D.24
4.如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )
图4-2-88
A.9 B.10 C.11 D.12
学生进行当堂检测,完成后,教师进行批阅,点评、讲解.
通过设置达标测评,进一步巩固所学新知,同时检测学习效果,做到“堂堂清”.
活动
四:
课堂
总结
反思
1.课堂总结:
(1)本节课主要学习了哪些知识?
(2)本节课还有哪些疑惑?说一说.
2.布置作业:教材P128练习.
注重课堂小结,激发学生参与的主动性,为每一个学生的发展与表现创造机会.
【知识网络】
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
教学过程沿着复习回顾—情境引入—探究新知—课堂训练—课堂总结的线索,使学生真正成为学习的主人,让学生充分进行讨论交流,在自主探索和合作学习中感受由视图到立体图形的过程.
②[讲授效果反思]
在例1和例2的难点处理上,教师引导,在师生交流合作中营造互动的氛围,让学生主动参与教学的整个过程,使他们的学习态度、情感意志、个性品质都得到不同程度的提高.
③[师生互动反思]
从课堂交流和课堂检测来看,学生能够根据三视图确定出它的立体图形,并且效果很好.
④[习题反思]
好题题号________________________________________
错题题号________________________________________
反思,更进一步提升.
2.由视图到立体图形
课题
2.由视图到立体图形
授课人
教
学
目
标
知识技能
会根据立体图形的三视图描述出实际的立体图形.
数学思考
通过本节课的学习,让学生通过感知、观察、实验、操作等数学活动充分感受数学在实际生活中的运用.
问题解决
尝试从不同角度寻求解决问题的方法,通过对解决问题过程的反思,获得解决问题的经验.
情感态度
在学习与探讨的过程中体验数学问题的探索性与创造性.通过学生之间的交流与合作,培养学生在独立思考问题的基础上能够聆听与理解他人的意见,并学会与他人合作,在合作中体验成功的喜悦,建立自信心.
教学
重点
会通过立体图形的三视图描述出实际的立体图形.
教学
难点
通过立体图形的三视图描述由一些几何体组合的立体图形.
授课
类型
新授课
课时
教具
多媒体
教学活动
教学
步骤
师生活动
设计意图
回顾
【知识回顾】
试画出粉笔的三视图(如图).
图4-2-76
复习前面所学习的立体图形的三视图的画法,为进入新课的做好准备.
活动
一:
创设
情境
导入
新课
【课堂引入】
(多媒体展示)“盲人摸象”是大家非常熟悉的成语故事.在实际生活中,如果我们对一个事物没有做到全面了解,那么我们很有可能犯盲人一样的错误.对于数学学习也是一样,请看下面的问题:如果你只看到图4-2-77,你会想到什么立体图形?接下来再看如图4-2-78所示的两个图形的左视图,你有什么发现?
图4-2-77 图4-2-78
处理方式:图4-2-77只是从一个方向看得到的平面图形,所以在此必须引导学生从多个方面去思考,逐渐培养学生的发散性思维.
创设情境,激发学生的求知欲,引导学生主动探索和解决问题,引入新课.
活动
二:
实践
探究
交流
新知
从引例中可以发现,根据一个平面图形可以联想到许多的立体图形,如图4-2-77中的长方形,可以是圆柱、正方体、其他的棱柱的左视图.要准确判断一个立体图形就必须用三视图的各个图形来综合判断.
课件出示:一个几何体由几个大小相同的小立方块搭成,其左视图和俯视图如图4-2-79所示.请搭出满足条件的几何体.你搭的几何体由几个小立方块搭成?与同伴交流.
图4-2-79
处理方式:学生读题,然后开展小组活动,利用手中的小立方体尝试搭出满足条件的几何体.教师巡视,并适时的进行指导,引导学生尝试各种可能,最后组织学生进行交流,最终发现:该几何体是由5块或6块小立方体搭成的,共有三种搭法.
注意事项:本问题相对而言难度较高,根据学生的状况,教师可以进行灵活的处理,如果学生不具备解决该问题的空间想象能力,建议还是让学生先自己搭出符合要求的几何体,再通过观察解决;如果学生空间想象能力许可,可以让学生直接想象该几何体的形状,然后解释你所想象的几何体,根据解释搭出符合要求的几何体;如果学生的空间想象能力更好,可以让学生先自主脱离实物解决该问题,然后进行交流.教无定法,关键在于了解学生,选择适合学生的方法.
由视图到立体图形更需要学生具有空间想象能力,或者说要求学生对一些基本图形更加熟悉,所以培养学生的图感仍是重中之重.
活动
二:
实践
探究
交流
新知
试一试:
1.如图4-2-80所示是一些立体图形的三视图,请根据视图说出立体图形的名称,并画出相应的实际立体图形.
(1) (2)
图4-2-80
2.如图4-2-81是一个物体的三视图,试说出该物体的形状.
图4-2-81
抽象思维及平面图形如何相互组合成立体图形,这一过程是了一个充分思维的过程.
活动
三:
开放
训练
体现
应用
【应用举例】
例1 (教材P127例3)图4-2-82所示的是一些立体图形的三视图,请根据视图说出立体图形的名称.
(1)
(2)
图4-2-82
学以致用,感受不同的方向观察几何体的不同性.已知部分形状图及有关数据信息,反向思考几何体的构成,从而力图让学生逐步脱离实物观察,迫使学生进入真正的想象层面,提高空间想象能力.
【拓展提升】
例2 如图4-2-83所示是由几个大小相同的立方块所搭几何体的俯视图,小正方形中的数字表示在该位置上小立方块的个数.请画出相应的几何体的主视图和左视图.
图4-2-83
在此过程中,通过由问题到模型,由模型再到脱离模型,较为完整地反映出一个问题解决的全貌.
活动
三:
开放
训练
体现
应用
【达标测评】
1.如图4-2-84所示的是某几何体的三视图,则该几何体的形状是( )
A.长方体 B.三棱柱 C.圆锥 D.正方体
图4-2-84 图4-2-85
2.由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上小正方体的个数,那么该几何体的左视图是( )
A B C D
图4-2-86
3.一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )
图4-2-87
A.6 B.8 C.12 D.24
4.如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )
图4-2-88
A.9 B.10 C.11 D.12
学生进行当堂检测,完成后,教师进行批阅,点评、讲解.
通过设置达标测评,进一步巩固所学新知,同时检测学习效果,做到“堂堂清”.
活动
四:
课堂
总结
反思
1.课堂总结:
(1)本节课主要学习了哪些知识?
(2)本节课还有哪些疑惑?说一说.
2.布置作业:教材P128练习.
注重课堂小结,激发学生参与的主动性,为每一个学生的发展与表现创造机会.
【知识网络】
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
教学过程沿着复习回顾—情境引入—探究新知—课堂训练—课堂总结的线索,使学生真正成为学习的主人,让学生充分进行讨论交流,在自主探索和合作学习中感受由视图到立体图形的过程.
②[讲授效果反思]
在例1和例2的难点处理上,教师引导,在师生交流合作中营造互动的氛围,让学生主动参与教学的整个过程,使他们的学习态度、情感意志、个性品质都得到不同程度的提高.
③[师生互动反思]
从课堂交流和课堂检测来看,学生能够根据三视图确定出它的立体图形,并且效果很好.
④[习题反思]
好题题号________________________________________
错题题号________________________________________
反思,更进一步提升.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
