4.6.3 余角和补角 课件(共24张PPT)
文档属性
| 名称 | 4.6.3 余角和补角 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 465.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-11 10:59:17 | ||
图片预览








文档简介
课件24张PPT。4.6 角余角和补角余角和补角的定义
余角、补角的性质
余角和补角的应用 1知识点余角和补角的定义 定义:两个角的和等于90°(直角),就说这两个角
互为余角,简称互余.如果两个角的和等于180°(平
角),就说这两个角互为补角,简称互补.知识点 例1 下列说法正确的有( )
①锐角的余角是锐角,锐角的补角是锐角;②
直角没有补角;③钝角没有余角,钝角的补角
是锐角;④直角的补角还是直角;⑤一个锐角
的补角与它的余角的差为90°;⑥两个角相
等,它们的补角也相等.
A.3个 B.4个 C.5个 D.6个
导引:主要紧扣锐角、钝角、余角、补角的特征进行
判断,除①②不正确外,其他说法都正确.B总 结 因为互余的两个角之和为90°,所以这两个角都
为锐角;因为互补的两个角之和为180°,所以这两个
角为一个锐角一个钝角或两个角都为直角. 知识点例2 已知∠α =50°17′,求 ∠α的余角和补角.
解: ∠α的余角=90°-50°17′=39°43′,
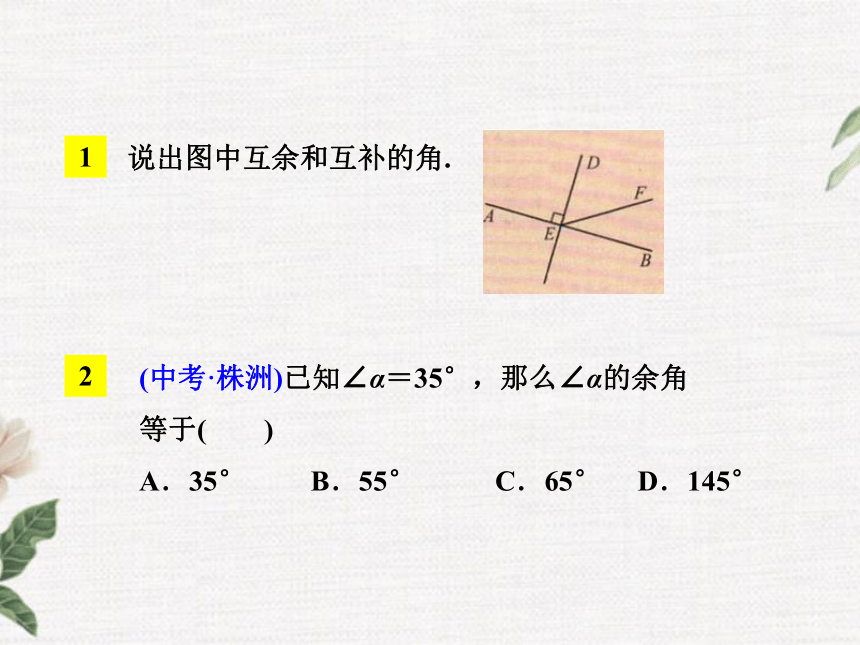
∠α的补角=180°- 50°17′=129°43′.1说出图中互余和互补的角.(中考·株洲)已知∠α=35°,那么∠α的余角
等于( )
A.35° B.55° C.65° D.145°23(中考·崇左)下列各图中,∠1与∠2互为余角的是( )
(中考·玉林)下面角的图示中,能与30°角互补的是( )45下列说法错误的是( )
A.互余的两个角都是锐角
B.一个角的补角大于这个角本身
C.互为补角的两个角不可能都是锐角
D.互为补角的两个角不可能都是钝角2知识点余角、补角的性质 1.余角的性质:同角的余角相等,即:若∠A+∠B=
90°,∠A+∠C=90°,则∠B=∠C.等角的余角相
等,即:若∠A+∠B=90°,∠D+∠C=90°,∠A
=∠D,则∠B=∠C.知识点2.补角的性质:同角的补角相等,即:若∠A+∠B=
180°,∠A+∠C=180°,则∠B=∠C.等角的补角
相等,即:若∠A+∠B=180°,∠D+∠C=
180°,∠A=∠D,则∠B=∠C.
知识点 例3 下列说法错误的是( )
A.同角或等角的余角相等
B.同角或等角的补角相等
C.两个锐角的余角相等
D.两个直角的补角相等
导引:A,B,D均正确,C中如果两个锐角不相等,那
么它们的余角也不相等,所以C错误.故选C.C总 结依据余角、补角的性质直接判断即可. 知识点例4 若∠1与∠2互补,∠2与∠3互补,∠1=
50°,则∠3等于( )
A.50° B.130°C.40° D.140°
导引:因为∠1+∠2=180°,∠2+∠3=180°,
所以∠3=∠1=50°.故选A.A总 结 由∠1、∠3都与∠2互补,应想到用补角
的性质,即同角的补角相等来解题.1若∠α+∠β=90°,∠β+∠γ=90°,则∠α与∠γ的关系是( )
A.互余 B.互补 C.相等 D.∠α=90°+∠γ
如图,直线AB,CD交于点O,因为
∠1+∠3=180°,∠2+∠3=180°,
所以∠1=∠2的依据是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等23如图所示,∠AOB=∠COD=90°,那么
∠AOC=∠BOD,这是根据( )
A.直角都相等 B.同角的余角相等
C.同角的补角相等 D.互为余角的两个角相等
如图所示,点O在直线AE上,OB平分
∠AOC,∠BOD=90°,则∠DOE和
∠COB的关系是( )
A.互余 B.互补 C.相等 D.和是钝角43知识点余角和补角的应用 例5 如图①,直线AB与∠COD的两边
OC,OD分别相交于点E,F,∠1+
∠2=180°.找出图中与∠2相等的角,
并说明理由.
导引:已知∠1+∠2=180°,说明∠2是∠1的补
角.根据同角(或等角)的补角相等,找出图中
∠1的其他补角和∠2的其他补角的补角,便可
确定与∠2相等的角.解:如图②,因为∠1+∠3=180°,∠1+∠2=
180°,所以∠3=∠2.
因为∠1+∠4=180°,∠1+∠2=180°,
所以∠4=∠2.
因为∠2+∠5=180°,∠6+∠5=180°,
所以∠2=∠6.
所以图中与∠2相等的角有∠3,∠4,∠6.总 结 “同角(或等角)的余角相等”“同角(或
等角)的补角相等”的实质是等量代换,只不
过在特定的背景下使用起来更便捷罢了.1如图,有两堵围墙,有人想测量地面上所形成的
∠AOB的度数,但人又不能进入围墙,只能站在
墙外,请问该如何测量?2如图,直线AB与CD相交于O点,
∠EOB=90°,则图中∠1与∠2的
关系是( )
A.互补 B.互余 C.相等 D.无法确定3(中考·厦门)如图,在三角形ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )
A.∠A和∠B互为补角
B.∠B和∠ADE互为补角
C.∠A和∠ADE互为余角
D.∠AED和∠DEB互为余角(中考·绥化)将一副三角尺按下列方式进行摆放,∠1,∠2不一定互补的是( )41.余角、补角理解要点:
(1)互余和互补是指两个角的数量关系,而不是多角之
间的关系.
(2)互余、互补的两个角,只与它们的数量(和)有关,
与它们的位置无关.
2.求一个角的余角或补角的方法:
我们在求有关图形的角度问题时,通常把一个角设为
未知数,表示出其他角,进而利用方程求解,这时我
们用到的便是方程思想.方程思想是指所求问题通过
列方程求解的一种思维方法,是解几何问题的重要策略.
余角、补角的性质
余角和补角的应用 1知识点余角和补角的定义 定义:两个角的和等于90°(直角),就说这两个角
互为余角,简称互余.如果两个角的和等于180°(平
角),就说这两个角互为补角,简称互补.知识点 例1 下列说法正确的有( )
①锐角的余角是锐角,锐角的补角是锐角;②
直角没有补角;③钝角没有余角,钝角的补角
是锐角;④直角的补角还是直角;⑤一个锐角
的补角与它的余角的差为90°;⑥两个角相
等,它们的补角也相等.
A.3个 B.4个 C.5个 D.6个
导引:主要紧扣锐角、钝角、余角、补角的特征进行
判断,除①②不正确外,其他说法都正确.B总 结 因为互余的两个角之和为90°,所以这两个角都
为锐角;因为互补的两个角之和为180°,所以这两个
角为一个锐角一个钝角或两个角都为直角. 知识点例2 已知∠α =50°17′,求 ∠α的余角和补角.
解: ∠α的余角=90°-50°17′=39°43′,
∠α的补角=180°- 50°17′=129°43′.1说出图中互余和互补的角.(中考·株洲)已知∠α=35°,那么∠α的余角
等于( )
A.35° B.55° C.65° D.145°23(中考·崇左)下列各图中,∠1与∠2互为余角的是( )
(中考·玉林)下面角的图示中,能与30°角互补的是( )45下列说法错误的是( )
A.互余的两个角都是锐角
B.一个角的补角大于这个角本身
C.互为补角的两个角不可能都是锐角
D.互为补角的两个角不可能都是钝角2知识点余角、补角的性质 1.余角的性质:同角的余角相等,即:若∠A+∠B=
90°,∠A+∠C=90°,则∠B=∠C.等角的余角相
等,即:若∠A+∠B=90°,∠D+∠C=90°,∠A
=∠D,则∠B=∠C.知识点2.补角的性质:同角的补角相等,即:若∠A+∠B=
180°,∠A+∠C=180°,则∠B=∠C.等角的补角
相等,即:若∠A+∠B=180°,∠D+∠C=
180°,∠A=∠D,则∠B=∠C.
知识点 例3 下列说法错误的是( )
A.同角或等角的余角相等
B.同角或等角的补角相等
C.两个锐角的余角相等
D.两个直角的补角相等
导引:A,B,D均正确,C中如果两个锐角不相等,那
么它们的余角也不相等,所以C错误.故选C.C总 结依据余角、补角的性质直接判断即可. 知识点例4 若∠1与∠2互补,∠2与∠3互补,∠1=
50°,则∠3等于( )
A.50° B.130°C.40° D.140°
导引:因为∠1+∠2=180°,∠2+∠3=180°,
所以∠3=∠1=50°.故选A.A总 结 由∠1、∠3都与∠2互补,应想到用补角
的性质,即同角的补角相等来解题.1若∠α+∠β=90°,∠β+∠γ=90°,则∠α与∠γ的关系是( )
A.互余 B.互补 C.相等 D.∠α=90°+∠γ
如图,直线AB,CD交于点O,因为
∠1+∠3=180°,∠2+∠3=180°,
所以∠1=∠2的依据是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等23如图所示,∠AOB=∠COD=90°,那么
∠AOC=∠BOD,这是根据( )
A.直角都相等 B.同角的余角相等
C.同角的补角相等 D.互为余角的两个角相等
如图所示,点O在直线AE上,OB平分
∠AOC,∠BOD=90°,则∠DOE和
∠COB的关系是( )
A.互余 B.互补 C.相等 D.和是钝角43知识点余角和补角的应用 例5 如图①,直线AB与∠COD的两边
OC,OD分别相交于点E,F,∠1+
∠2=180°.找出图中与∠2相等的角,
并说明理由.
导引:已知∠1+∠2=180°,说明∠2是∠1的补
角.根据同角(或等角)的补角相等,找出图中
∠1的其他补角和∠2的其他补角的补角,便可
确定与∠2相等的角.解:如图②,因为∠1+∠3=180°,∠1+∠2=
180°,所以∠3=∠2.
因为∠1+∠4=180°,∠1+∠2=180°,
所以∠4=∠2.
因为∠2+∠5=180°,∠6+∠5=180°,
所以∠2=∠6.
所以图中与∠2相等的角有∠3,∠4,∠6.总 结 “同角(或等角)的余角相等”“同角(或
等角)的补角相等”的实质是等量代换,只不
过在特定的背景下使用起来更便捷罢了.1如图,有两堵围墙,有人想测量地面上所形成的
∠AOB的度数,但人又不能进入围墙,只能站在
墙外,请问该如何测量?2如图,直线AB与CD相交于O点,
∠EOB=90°,则图中∠1与∠2的
关系是( )
A.互补 B.互余 C.相等 D.无法确定3(中考·厦门)如图,在三角形ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )
A.∠A和∠B互为补角
B.∠B和∠ADE互为补角
C.∠A和∠ADE互为余角
D.∠AED和∠DEB互为余角(中考·绥化)将一副三角尺按下列方式进行摆放,∠1,∠2不一定互补的是( )41.余角、补角理解要点:
(1)互余和互补是指两个角的数量关系,而不是多角之
间的关系.
(2)互余、互补的两个角,只与它们的数量(和)有关,
与它们的位置无关.
2.求一个角的余角或补角的方法:
我们在求有关图形的角度问题时,通常把一个角设为
未知数,表示出其他角,进而利用方程求解,这时我
们用到的便是方程思想.方程思想是指所求问题通过
列方程求解的一种思维方法,是解几何问题的重要策略.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
