5.2.4平行线的判定与性质的综合应用 课件(30张PPT)
文档属性
| 名称 | 5.2.4平行线的判定与性质的综合应用 课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 383.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-11 10:59:17 | ||
图片预览










文档简介
(共30张PPT)
5.2 平行线
平行线的判定与性质的综合应用
平行线的性质的应用
平行线的判定的应用
平行线的性质与判定的综合应用
1
知识点
平行线的性质的应用
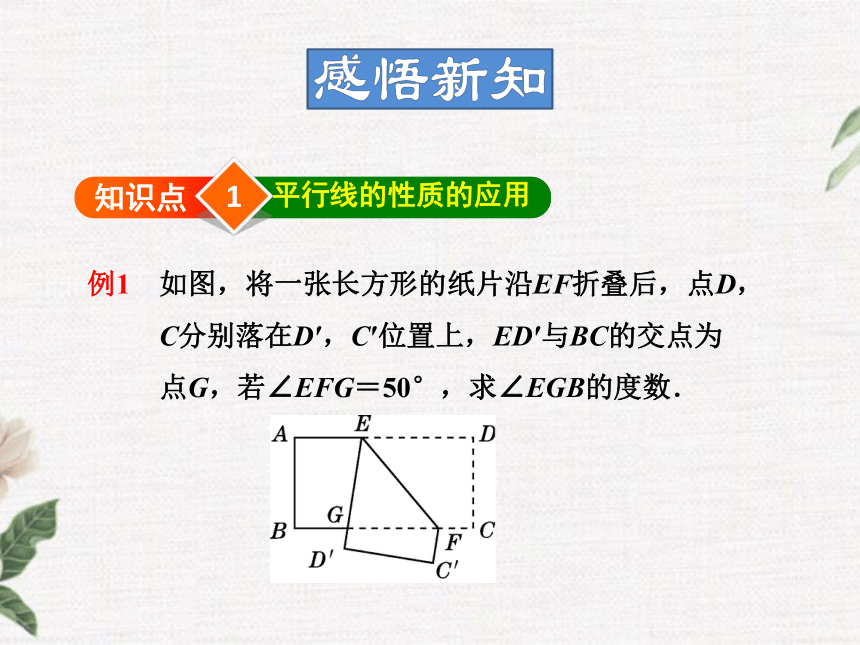
例1 如图,将一张长方形的纸片沿EF折叠后,点D,
C分别落在D′,C′位置上,ED′与BC的交点为
点G,若∠EFG=50°,求∠EGB的度数.
导引:本题根据长方形的对边是平行的,利用平行线
的性质:两直线平行,内错角相等,先求
∠DEF=50°,再根据折叠前后的对应角相等
求得∠D′EF=50°,然后根据平角的定义得
∠AEG=80°,最后根据两直线平行,同旁内
角互补求得∠EGB=100°.
解:∵四边形ABCD是长方形(已知),
∴∠A=∠B=90°(长方形的定义).
∴∠A+∠B=180°,
∴AD∥BC(同旁内角互补,两直线平行).
∴∠DEF=∠EFG(两直线平行,内错角相等).
∵∠EFG=50°(已知),
∴∠DEF=50°(等量代换).
∵∠DEF=∠D′EF(折叠的性质),
∴∠D′EF=50°(等量代换).
∴∠AEG=180°-∠DEF-∠D′EF=80°(平角的定义).
又∵AD∥BC,
∴∠AEG+∠EGB=180°(两直线平行,同旁内角互补),
∴∠EGB=180°-∠AEG=180°-80°=100°.
总 结
解决折叠问题的关键是找到折叠前后相等的角,
然后熟练利用平行线的性质来求角的度数.
平移作图的一般步骤:
平移作图是平移基本性质的应用,利用平移可以得
到许多美丽的图案,在具体作图时,应抓住作图的“四
部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接
点);
(3)移:过关键点作平行且相等的线段,得到关键点的对
应点;
(4)连:按原图顺次连接对应点.
例2 如图,四边形ABCD的顶点A移动到了A′处,
作出四边形ABCD平移后的图形.
导引:∵点A移动到了A′处,∴平移的
方向就是AA′方向,平移的距离
就是线段AA′的长度,要作出平移后的图形,需要先
作出点B,C,D的对应点B′,C′,D′,由“对应点
所连的线段平行且相等”可知,BB′∥CC′∥DD′∥
AA′,BB′=CC′=DD′=AA′,据此可作出点B′,C′,
D′,再顺次连接A′,B′,C′,D′即可.
解:(1)连接AA′;
(2)分别过点B,C,D作BB′∥AA′,
CC′∥AA′,DD′∥AA′;
(3)在BB′上沿射线AA′的方向截取BB′=AA′,
在CC′,DD′上按同样的方法截取CC′=AA′,
DD′=AA′;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,即得到
四边形ABCD平移后的图形,如图.
总 结
画平移图形的方法:首先分析题目的要求,找
出平移的方向和距离,再分析已知图形,确定构成
图形的关键点,然后根据平移方向和距离平移每个
关键点,最后顺次连接所作的每个关键点的对应点,
并标出相应的字母,得出平移后的图形.
1
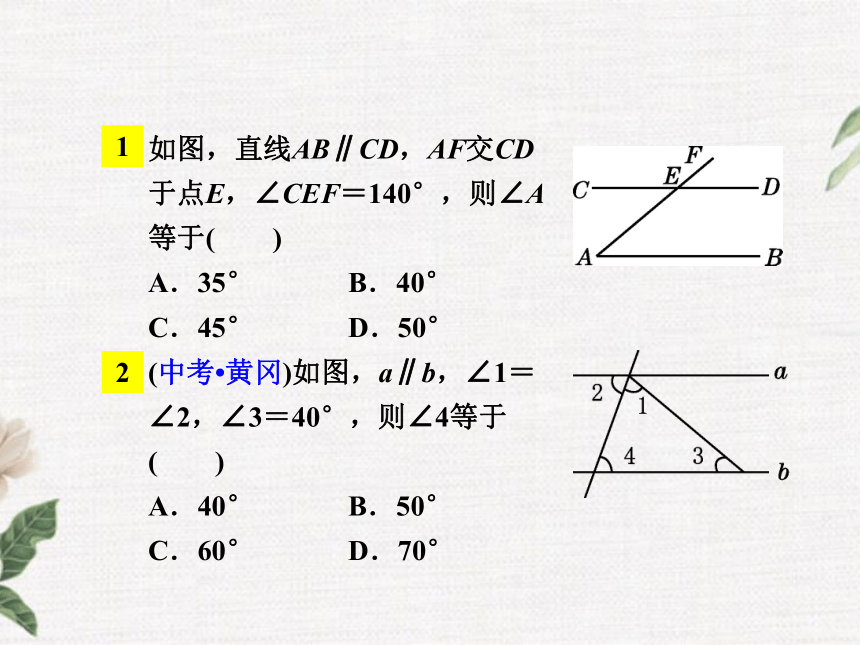
如图,直线AB∥CD,AF交CD
于点E,∠CEF=140°,则∠A
等于( )
A.35° B.40°
C.45° D.50°
(中考 黄冈)如图,a∥b,∠1=
∠2,∠3=40°,则∠4等于
( )
A.40° B.50°
C.60° D.70°
2
3
(中考 十堰)如图,AB∥CD,点E
在线段BC上,若∠1=40°,∠2
=30°,则∠3的度数是( )
A.70° B.60° C.55° D.50°
如图是我们生活中经常接触的小刀,
刀柄的外形是一个直角梯形(挖去一
个半圆形),刀片上、下两边是平行
的,转动刀片时形成∠1、∠2,则
∠1+∠2=________.
4
2
知识点
平行线的判定的应用
例3 如图所示,∠B=∠D,∠CEF=∠A.
试问CD与EF平行吗?为什么?
导引:1.要说明CD∥EF,我们无法找出相等的同位
角、内错角,也无法说明其同旁内角互补,
因此需找第三条直线与它们平行(即AB∥CD,
AB∥EF),这都能由已知∠B=∠D,
∠CEF=∠A说明.
2.由已知∠B=∠D,∠CEF=∠A很容易就能
得出AB∥CD及EF∥AB,再由如果两条直线
都和第三条直线平行,那么这两条直线也互
相平行就可得到CD∥EF.
解:CD∥EF,理由:
∵∠B=∠D,
∴AB∥CD(内错角相等,两直线平行).
∵∠CEF=∠A,
∴EF∥AB(同位角相等,两直线平行).
∴CD∥EF(平行于同一条直线的两条直线平
行).
总 结
找寻说明平行的方法:
1.分析法:由结论往前推,要说明这个结论成立需要什么样
的条件,一直递推到已知条件为止;(如导引1)
2.综合法:由已知条件一步一步往后推理,看这个已知条件
能推出什么结论,一直推导出要说明的结论为止;(如导引2)
注:当遇到复杂问题的时候,我们常常将分析法和综合
法同时进行,即由两头向中间推,寻找到中间的结合点.
例4 光线从空气射入水中时,传播方向会发生改变,
这种现象叫做光的折射现象.同样,光线从水
中射入空气中时,也会发生折射现象,一束光
线从空气射入水中再从水中射入空气中时,光
线的传播方向如图,其中,直线a,b都表示空
气与水的分界面.已知∠1=
∠4,∠2=∠3,请你判断光
线c与d是否平行?为什么?
导引:设光线在水中的部分为e,e与直线a所成的钝
角为∠5,e与直线b所成的钝角为∠6,只要
能说明∠1+∠5=∠4+∠6,则根据“内错
角相等,两直线平行”即可判定c∥d.
解:c∥d.理由如下:
如图,设光线在水中的部分为e.
∵∠2+∠5=180°,∠3+∠6=180°,
∠2=∠3,
∴∠5=∠6(等角的补角相等).
又∵∠1=∠4,
∴∠1+∠5=∠4+∠6.
∴c∥d(内错角相等,两直线平行).
总 结
判断光线c与d是否平行,应首先解决两个关键问
题,一是把实物图抽象为“三线八角”的基本图形;
二是把直线c,d看作被直线e所截的两条直线.如此,
问题转化为说明∠1+∠5=∠4+∠6.
1
如图,已知BE平分∠ABC,
CF平分∠BCD,∠1=∠2,
那么直线AB与CD的位置关
系是________.
(改编 江西)一大门的栏杆如
图所示,BA垂直地面AE于A,
要使CD平行于地面AE,则
∠ABC+∠BCD=________度.
2
3
知识点
平行线的性质与判定的综合应用
例5 如图,已知∠ABC与∠ECB互补,∠1=∠2,
则∠P与∠Q一定相等吗?说说你的理由.
导引:如果∠P和∠Q相等,那么PB∥
CQ,∴要判断∠P与∠Q是否相
等,只需判断PB和CQ是否平行.
要说明PB∥CQ,可以通过说明
∠PBC=∠BCQ来实现,由于∠1=∠2,因此
只需说明∠ABC=∠BCD即可.
解:∠P=∠Q.
理由如下:∵∠ABC与∠ECB互补(已知),
∴AB∥ED(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠ABC-∠1=∠BCD-∠2(等式的性质),
即∠PBC=∠BCQ.
∴PB∥CQ(内错角相等,两直线平行).
∴∠P=∠Q(两直线平行,内错角相等).
总 结
一个数学问题的构成含有四个要素:题目的条
件、解题的依据、解题的方法、题目的结论,如果
题目所含的四个要素解题者已经知道或者结论虽未
指明,但它是完全确定的,这样的问题就是封闭性
的数学问题.
例6 如图,AB∥DE,则∠BCD,∠B,∠D的
大小关系如何?为什么?
导引:本题涉及两直线平行,要研究角之间的大小
关系,可考虑研究同位角、内错角和同旁内
角,可考虑作辅助线构造出同位角、内错角
和同旁内角解决问题.
解:∠BCD=∠B-∠D.
理由:如图,过点C作CF∥AB.
∵CF∥AB,
∴∠B=∠BCF(两直线平行,内错角相等).
∵AB∥DE,CF∥AB,
∴CF∥DE(平行于同一条直线的两条直线平行).
∴∠DCF=∠D(两直线平行,内错角相等).
∴∠B-∠D=∠BCF-∠DCF(等式的性质).
∵∠BCD=∠BCF-∠DCF,
∴∠BCD=∠B-∠D.
总 结
已知图形中有平行线和折线或拐角时,常过折
点或拐点作平行线,构造出同位角、内错角或同旁
内角,这样就可以利用角之间的关系求解.
1
(中考 河南)如图,直线a,b
被直线c,d所截,若∠1=
∠2,∠3=125°,则∠4的
度数为( )
A.55° B.60° C.70° D.75°
如图,已知AB∥CD,∠1=30°,
∠2=90°,则∠3等于( )
A.60° B.50°
C.45° D.30°
2
3
如图,如果AB∥DE,∠1=∠2,那么AE∥
DC,请说明理由.
从图形中得出结论是图形的性质;而从具备
什么条件推理出图形是图形的判定;特别说明,
图形的定义既是图形的判定,也是图形的性质;
即:条件
结论.
图形
5.2 平行线
平行线的判定与性质的综合应用
平行线的性质的应用
平行线的判定的应用
平行线的性质与判定的综合应用
1
知识点
平行线的性质的应用
例1 如图,将一张长方形的纸片沿EF折叠后,点D,
C分别落在D′,C′位置上,ED′与BC的交点为
点G,若∠EFG=50°,求∠EGB的度数.
导引:本题根据长方形的对边是平行的,利用平行线
的性质:两直线平行,内错角相等,先求
∠DEF=50°,再根据折叠前后的对应角相等
求得∠D′EF=50°,然后根据平角的定义得
∠AEG=80°,最后根据两直线平行,同旁内
角互补求得∠EGB=100°.
解:∵四边形ABCD是长方形(已知),
∴∠A=∠B=90°(长方形的定义).
∴∠A+∠B=180°,
∴AD∥BC(同旁内角互补,两直线平行).
∴∠DEF=∠EFG(两直线平行,内错角相等).
∵∠EFG=50°(已知),
∴∠DEF=50°(等量代换).
∵∠DEF=∠D′EF(折叠的性质),
∴∠D′EF=50°(等量代换).
∴∠AEG=180°-∠DEF-∠D′EF=80°(平角的定义).
又∵AD∥BC,
∴∠AEG+∠EGB=180°(两直线平行,同旁内角互补),
∴∠EGB=180°-∠AEG=180°-80°=100°.
总 结
解决折叠问题的关键是找到折叠前后相等的角,
然后熟练利用平行线的性质来求角的度数.
平移作图的一般步骤:
平移作图是平移基本性质的应用,利用平移可以得
到许多美丽的图案,在具体作图时,应抓住作图的“四
部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接
点);
(3)移:过关键点作平行且相等的线段,得到关键点的对
应点;
(4)连:按原图顺次连接对应点.
例2 如图,四边形ABCD的顶点A移动到了A′处,
作出四边形ABCD平移后的图形.
导引:∵点A移动到了A′处,∴平移的
方向就是AA′方向,平移的距离
就是线段AA′的长度,要作出平移后的图形,需要先
作出点B,C,D的对应点B′,C′,D′,由“对应点
所连的线段平行且相等”可知,BB′∥CC′∥DD′∥
AA′,BB′=CC′=DD′=AA′,据此可作出点B′,C′,
D′,再顺次连接A′,B′,C′,D′即可.
解:(1)连接AA′;
(2)分别过点B,C,D作BB′∥AA′,
CC′∥AA′,DD′∥AA′;
(3)在BB′上沿射线AA′的方向截取BB′=AA′,
在CC′,DD′上按同样的方法截取CC′=AA′,
DD′=AA′;
(4)顺次连接A′B′,B′C′,C′D′,D′A′,即得到
四边形ABCD平移后的图形,如图.
总 结
画平移图形的方法:首先分析题目的要求,找
出平移的方向和距离,再分析已知图形,确定构成
图形的关键点,然后根据平移方向和距离平移每个
关键点,最后顺次连接所作的每个关键点的对应点,
并标出相应的字母,得出平移后的图形.
1
如图,直线AB∥CD,AF交CD
于点E,∠CEF=140°,则∠A
等于( )
A.35° B.40°
C.45° D.50°
(中考 黄冈)如图,a∥b,∠1=
∠2,∠3=40°,则∠4等于
( )
A.40° B.50°
C.60° D.70°
2
3
(中考 十堰)如图,AB∥CD,点E
在线段BC上,若∠1=40°,∠2
=30°,则∠3的度数是( )
A.70° B.60° C.55° D.50°
如图是我们生活中经常接触的小刀,
刀柄的外形是一个直角梯形(挖去一
个半圆形),刀片上、下两边是平行
的,转动刀片时形成∠1、∠2,则
∠1+∠2=________.
4
2
知识点
平行线的判定的应用
例3 如图所示,∠B=∠D,∠CEF=∠A.
试问CD与EF平行吗?为什么?
导引:1.要说明CD∥EF,我们无法找出相等的同位
角、内错角,也无法说明其同旁内角互补,
因此需找第三条直线与它们平行(即AB∥CD,
AB∥EF),这都能由已知∠B=∠D,
∠CEF=∠A说明.
2.由已知∠B=∠D,∠CEF=∠A很容易就能
得出AB∥CD及EF∥AB,再由如果两条直线
都和第三条直线平行,那么这两条直线也互
相平行就可得到CD∥EF.
解:CD∥EF,理由:
∵∠B=∠D,
∴AB∥CD(内错角相等,两直线平行).
∵∠CEF=∠A,
∴EF∥AB(同位角相等,两直线平行).
∴CD∥EF(平行于同一条直线的两条直线平
行).
总 结
找寻说明平行的方法:
1.分析法:由结论往前推,要说明这个结论成立需要什么样
的条件,一直递推到已知条件为止;(如导引1)
2.综合法:由已知条件一步一步往后推理,看这个已知条件
能推出什么结论,一直推导出要说明的结论为止;(如导引2)
注:当遇到复杂问题的时候,我们常常将分析法和综合
法同时进行,即由两头向中间推,寻找到中间的结合点.
例4 光线从空气射入水中时,传播方向会发生改变,
这种现象叫做光的折射现象.同样,光线从水
中射入空气中时,也会发生折射现象,一束光
线从空气射入水中再从水中射入空气中时,光
线的传播方向如图,其中,直线a,b都表示空
气与水的分界面.已知∠1=
∠4,∠2=∠3,请你判断光
线c与d是否平行?为什么?
导引:设光线在水中的部分为e,e与直线a所成的钝
角为∠5,e与直线b所成的钝角为∠6,只要
能说明∠1+∠5=∠4+∠6,则根据“内错
角相等,两直线平行”即可判定c∥d.
解:c∥d.理由如下:
如图,设光线在水中的部分为e.
∵∠2+∠5=180°,∠3+∠6=180°,
∠2=∠3,
∴∠5=∠6(等角的补角相等).
又∵∠1=∠4,
∴∠1+∠5=∠4+∠6.
∴c∥d(内错角相等,两直线平行).
总 结
判断光线c与d是否平行,应首先解决两个关键问
题,一是把实物图抽象为“三线八角”的基本图形;
二是把直线c,d看作被直线e所截的两条直线.如此,
问题转化为说明∠1+∠5=∠4+∠6.
1
如图,已知BE平分∠ABC,
CF平分∠BCD,∠1=∠2,
那么直线AB与CD的位置关
系是________.
(改编 江西)一大门的栏杆如
图所示,BA垂直地面AE于A,
要使CD平行于地面AE,则
∠ABC+∠BCD=________度.
2
3
知识点
平行线的性质与判定的综合应用
例5 如图,已知∠ABC与∠ECB互补,∠1=∠2,
则∠P与∠Q一定相等吗?说说你的理由.
导引:如果∠P和∠Q相等,那么PB∥
CQ,∴要判断∠P与∠Q是否相
等,只需判断PB和CQ是否平行.
要说明PB∥CQ,可以通过说明
∠PBC=∠BCQ来实现,由于∠1=∠2,因此
只需说明∠ABC=∠BCD即可.
解:∠P=∠Q.
理由如下:∵∠ABC与∠ECB互补(已知),
∴AB∥ED(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠ABC-∠1=∠BCD-∠2(等式的性质),
即∠PBC=∠BCQ.
∴PB∥CQ(内错角相等,两直线平行).
∴∠P=∠Q(两直线平行,内错角相等).
总 结
一个数学问题的构成含有四个要素:题目的条
件、解题的依据、解题的方法、题目的结论,如果
题目所含的四个要素解题者已经知道或者结论虽未
指明,但它是完全确定的,这样的问题就是封闭性
的数学问题.
例6 如图,AB∥DE,则∠BCD,∠B,∠D的
大小关系如何?为什么?
导引:本题涉及两直线平行,要研究角之间的大小
关系,可考虑研究同位角、内错角和同旁内
角,可考虑作辅助线构造出同位角、内错角
和同旁内角解决问题.
解:∠BCD=∠B-∠D.
理由:如图,过点C作CF∥AB.
∵CF∥AB,
∴∠B=∠BCF(两直线平行,内错角相等).
∵AB∥DE,CF∥AB,
∴CF∥DE(平行于同一条直线的两条直线平行).
∴∠DCF=∠D(两直线平行,内错角相等).
∴∠B-∠D=∠BCF-∠DCF(等式的性质).
∵∠BCD=∠BCF-∠DCF,
∴∠BCD=∠B-∠D.
总 结
已知图形中有平行线和折线或拐角时,常过折
点或拐点作平行线,构造出同位角、内错角或同旁
内角,这样就可以利用角之间的关系求解.
1
(中考 河南)如图,直线a,b
被直线c,d所截,若∠1=
∠2,∠3=125°,则∠4的
度数为( )
A.55° B.60° C.70° D.75°
如图,已知AB∥CD,∠1=30°,
∠2=90°,则∠3等于( )
A.60° B.50°
C.45° D.30°
2
3
如图,如果AB∥DE,∠1=∠2,那么AE∥
DC,请说明理由.
从图形中得出结论是图形的性质;而从具备
什么条件推理出图形是图形的判定;特别说明,
图形的定义既是图形的判定,也是图形的性质;
即:条件
结论.
图形
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
