人教版数学八年级上第十二章全等三角形知识点+题案+作业讲义学案(无答案)
文档属性
| 名称 | 人教版数学八年级上第十二章全等三角形知识点+题案+作业讲义学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 370.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-12 08:37:58 | ||
图片预览


文档简介
第十二章 全等三角形
全等三角形
【全等三角形的概念和性质】
全等形:能够重合的两个图形.
全等三角形:能够重合的两个三角形.
把两个全等的三角形重合到一起时,重合的顶点称为对应点,
重合的边称为对应边,重合的角称为对应角。
全等三角形的性质:全等三角形的对应边相等,对应角相等;
表示方法:“全等”用“≌”表示,读作:_________;
【例题一】
(1)如图所示,△OCA≌△OBD,
对应顶点有:点 和点 ,点 和点 ,点 和点 ;
对应角有: 和 , 和 , 和 ;
对应边有: 和 , 和 , 和 .
(2)如图△ABD≌△CDB,若AB=4,AD=5,BD=6,∠ABD=50°,∠ADB=30°,则BC= ,CD= ,∠BDC= ,∠C= .
【基础练习一】
已知ABC≌EFD,若,,,,则 , .
如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )
A、α=β B、α=2β
C、α+β=90° D、α+2β=180°
下列说法错误的是( )
A、全等三角形的公共角是对应角,对顶角也是对应角
B、全等三角形的公共边也是对应边
C、全等三角形的公共点是对应顶点
D、全等三角形中相等的边所对的角是对应角,相等的角所对的边是对应边。
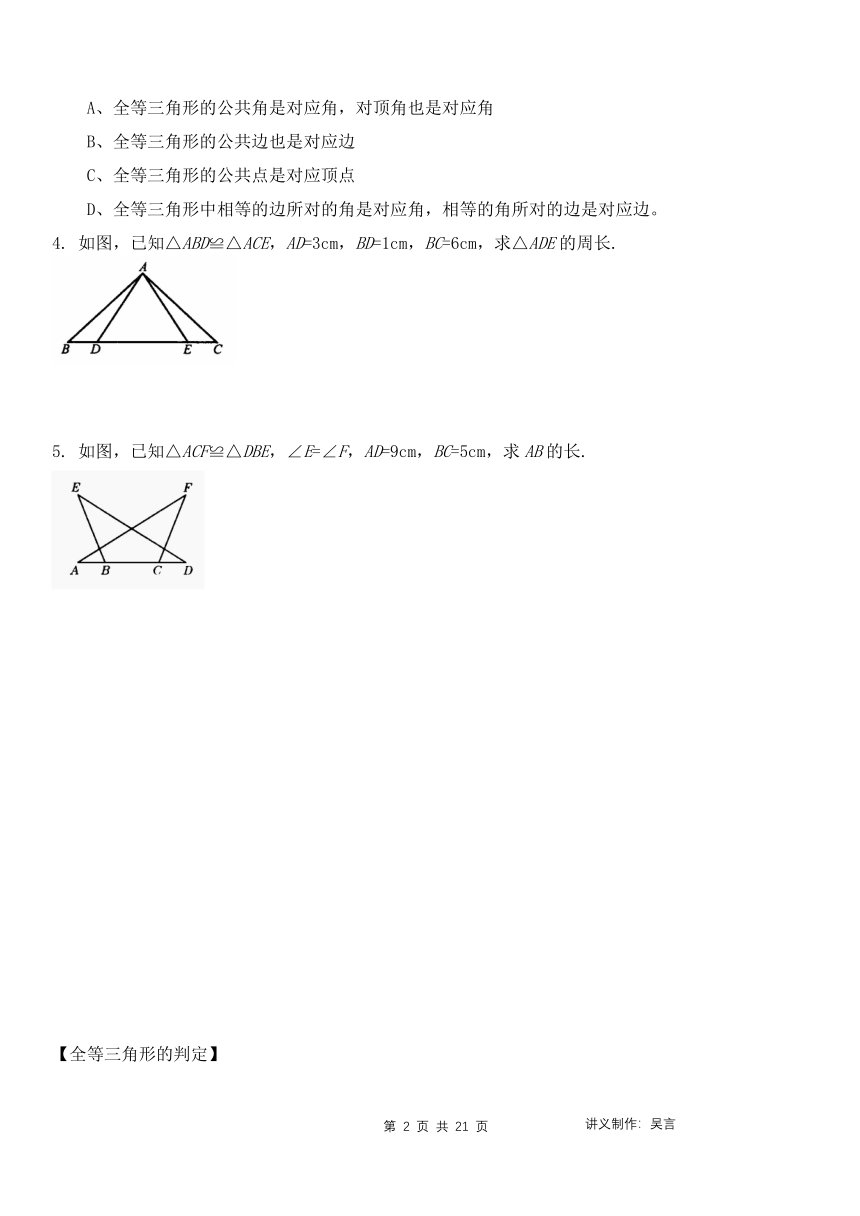
如图,已知△ABD≌△ACE,AD=3cm,BD=1cm,BC=6cm,求△ADE的周长.
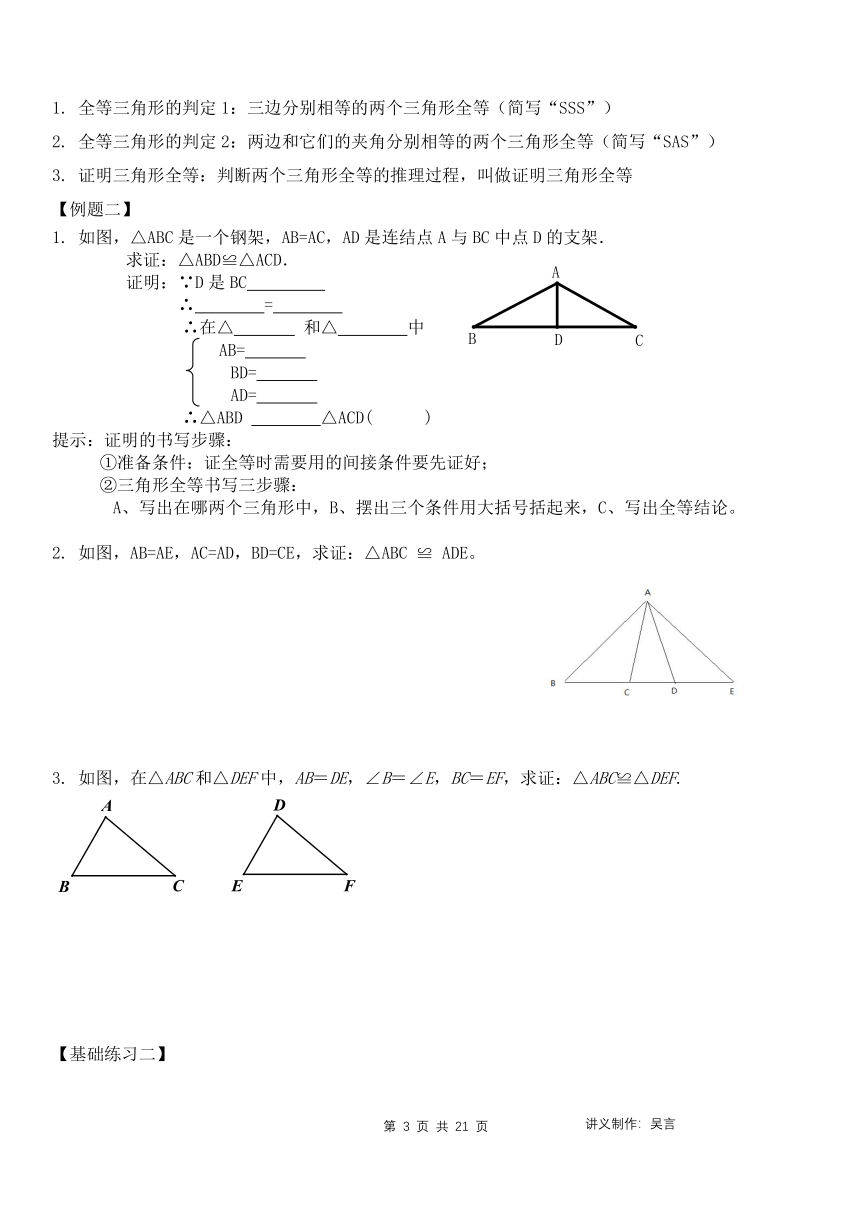
如图,已知△ACF≌△DBE,∠E=∠F,AD=9cm,BC=5cm,求AB的长.
【全等三角形的判定】
全等三角形的判定1:三边分别相等的两个三角形全等(简写“SSS”)
全等三角形的判定2:两边和它们的夹角分别相等的两个三角形全等(简写“SAS”)
证明三角形全等:判断两个三角形全等的推理过程,叫做证明三角形全等
【例题二】
如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
证明:∵D是BC
∴ =
∴在△ 和△ 中
AB=
BD=
AD=
∴△ABD △ACD( )
提示:证明的书写步骤:
①准备条件:证全等时需要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中,B、摆出三个条件用大括号括起来,C、写出全等结论。
如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ ADE。
如图,在△ABC和△DEF中,AB=DE,∠B=∠E,BC=EF,求证:△ABC≌△DEF.
【基础练习二】
如图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF,请将下面说明ΔABC≌ΔDEF的过程和理由补充完整。
解:∵BE=CF
∴BE+EC=CF+EC( )
即BC=EF
在ΔABC和ΔDEF中
AB=________ (________________)
__________=DF(_______________)
BC=__________
∴ΔABC≌ΔDEF (_____________)
如图,AC=AE,∠1=∠2,AB=AD.
求证:BC=DE.
如图,已知AB=AC,DB=EC试说明∠B=∠C的理由.
如图,已知点A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF.
说明:(1)AB∥DE ;(2)BC∥EF .
【课后作业1】
下列命题中:
(1)形状相同的两个三角形是全等形;
(2)在两个全等三角形中,相等的角是对应角,相等的边是对应边;
(3)全等三角形对应边上的高、中线及对应角平分线分别相等。
其中真命题的个数有( )
A.3个 B.2个 C.1个 D.0个
2.如图,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF。
则下列结论中,错误的是( )
A.BE=EC B.BC=EF
C.AC=DF D.△ABC≌△DEF
3.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150° B.180°
C.210° D.225°
4.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
A.∠B B.∠A
C.∠EMF D.∠AFB
6.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2 B.3 C.5 D.2.5
7. 如图,已知AB=DE,BC=EF,AF=DC,则∠EFD=∠BCA,请说明理由。
已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC
如图,AE=AF,AB=AC,∠A=60°,∠B=24°,求的度数.
四边形ABCD中,AC与BD相交于点F,E为AC上一点,且AD=AB,ED=EB.
求证:⑴ ≌ ⑵≌.
【全等三角形的判定】
全等三角形的判定3:两角和他们的夹边分别相等的两个三角形全等(简写“ASA”)
全等三角形的判定4:两角和其中一个角的对边分别相等的两个三角形全等(简写“AAS”)
直角三角形的判定5:斜边和一条直角边分别相等的两个直角三角形全等(简写“HL”)
【例题三】
如图,在△ABC和△DEF中,∠A=∠D,AB=DE,∠B=∠E,求证:△ABC≌△DEF.
如图,∠ADB=∠CDB,∠ABD=∠CBD,证明△ABD≌△CBD;
3.如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
【基础练习三】
如图,D是△ABC的边AB的中点,DE∥BC,CE∥AB,AC与DE相交于点F.求证:△ADF≌△CEF.
如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌CFE.
已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
如图,点B、E、C、F在同一直线上,若AB⊥BF,DE⊥BF,AB=DE,AC=DF.求证:△ABC≌△DEF.
已知:如图,ED⊥AB,FC⊥AB,垂足分别为D、C,AE∥BF,且AE=BF.求证:△AED≌△BFC.
如图,点C、E、B、F在一条直线上,AB⊥CF于B,DE⊥CF于E,AC=DF,AB=DE.求证:CE=BF.
【课后作业2】
如图,AC=DF,∠1=∠2,如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是( )
A.∠A=∠D B.AB=DE C.BF=CE D.∠B=∠E
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )
A.4 B.5 C.1 D.
如图,∠ADB=∠CDB,∠ABD=∠CBD,则△ABD≌△CBD的判定是( )
SSS B.SAS C.AAS D.ASA
如图,点C、F在BE上,BF=CE,∠A=∠D,∠B=∠E.求证:△ABC≌△DEF.
如图,GC=GE,BE=FC,∠B=∠F.求证:△ABC≌△DFE.
已知,如图:A、E、F、B在一条直线上,AE=BF,∠C=∠D,∠A=∠B,求证:△ACF≌△BDE.
已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.
已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:AF=CE.
9.如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,且BD=CD.试说明BE=CF.
【角平分线的性质与判定】
角平分线的性质:角平分线上的点到角两边的距离相等
角平分线的判定:角的内部到角的两边的距离相等的点在角平分线上
三角形的角平分线的性质:三角形的三条角平分线交于三角形内部一点,并且该点到三边的距离相等
【例题四】
如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
求证:AD是△ABC的角平分线.
如图,在△ABC中,AB=8,AC=6,O为△ABC角平分线的交点,若△ABO的面积为20,则△ACO的面积为
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,
求证:AD是∠BAC的平分线.
【基础练习四】
如图,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
求证:AP是∠BAC的角平分线.
2. 如图,∠B=∠C=90°,M是BC中点,DM平分∠ADC,求证:AM平分∠DAB.
3.如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,DE⊥AC于点E,BF∥DE交CD于点F.求证:DE=BF.
如图,AP,CP分别是△ABC外角∠MAC和∠NCA的平分线,它们交于点P.求证:BP为∠MBN的平分线.
已知:如图,△ABC的角平分线BE、CF相交于点P.求证:点P在∠A的平分线上.
如图,CD为△ABC斜边上的高,∠BAC的平分线分别交CD,BC于点E、F,FG⊥AB,垂足为点G.求证:CE=FG.
【课后作业3】
如图,OP为∠AOB的平分线,PC⊥OB于点C,且PC=3,点P到OA的距离为______.
如图,点P是∠AOB的角平分线OC上一点,PD⊥OA,垂足为点D,PD=2,M为OP的中点,则点M到射线OB的距离为( )
B.1 C. D.2
如图,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于( )
A.4 B.3 C.2 D.1
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为( )
B.2 C.3 D.2
如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,点E是AB上任意一点.若CD=5,则DE的最小值等于( )
A.2.5 B.4 C.5 D.10
如图,在Rt△ABC中,∠B=90°,CD是∠ACB的平分线,若BD=2,则D到AC的距离为 .
在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是 .
如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为 .
如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么点D到线段AB的距离是 cm.
如图,∠AOB=70°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ= °.
综合提高练习
【全等三角形】
如图,≌,,求的长和的度数。
如图,已知△ABC≌△DCB,如果∠ABC=72°,∠ACB=45°.
⑴求∠D的度数; ⑵求∠ABD的度数.
如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求角F的度数与DH的长;
(2)求证:AB∥DE.
如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,
(1)当DE=8,BC=5时,线段AE的长为 ;
(2)已知∠D=35°,∠C=60°,
①求∠DBC的度数;
②求∠AFD的度数.
已知:△ABC中,BD、CE分别是AC、AB边上的高,BQ=AC,点F在CE的延长线上,CF=AB,求证:AF⊥AQ.
如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN
如图,AC与BD相交于点E,AC=BD,AC⊥BC,BD⊥AD.垂足分别是C、D.
(1)若AD=6,求BC的长;
(2)求证:△ADE≌△BCE.
已知:如图,AC⊥CE,AB⊥BD,ED⊥BD,BC=DE,求证:△ABC≌△CDE.
已知:如图AC,BD相交于点O,∠A=∠D,AB=CD,
求证:△AOB≌△DOC.
如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
求证:角的平分线上的点到角的两边的距离相等.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,证明:
(1)CF=EB.
(2)AB=AF+2EB.
讲义制作:吴言
