第十四章阅读与思考:十字相乘法(同步课件)
文档属性
| 名称 | 第十四章阅读与思考:十字相乘法(同步课件) |  | |
| 格式 | zip | ||
| 文件大小 | 340.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-12 11:15:53 | ||
图片预览




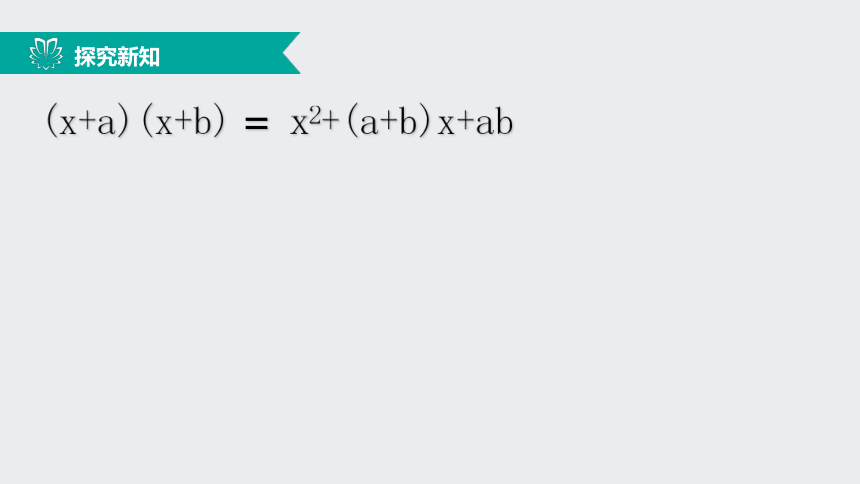


文档简介
课件14张PPT。授课:李卫老师人教版《数学》 八年级下册[慕联教育同步课程]
课程编号:TS1803010202R8114030301LWJ
慕课联盟课程开发中心:www.moocun.com阅读与思考:十字相乘法 1.理解十字相乘法的根据
2.能用十字相乘法分解二次三项式1.举例说明因式分解与整式乘法的关系2.我们已经学习了哪些因式分解的方法?
提公因式法: ma+mb+mc=m(a+b+c)
运用公式法: a2-b2=(a+b)(a-b)
a2 ±2ab+b2=(a ±b)21.(x+2)(x+1)=x2+3x+23.(x-2)(x+1)=x2-x-24.(x-2)(x-1)=x2-3x+22.(x+2)(x-1)=x2+x-25.(x+2)(x+3)=x2+5x+66.(x+2)(x-3)=x2-x-67.(x-2)(x+3)=x2+x-6(x+a)(x+b)=x2+(a+b)x+ab请直接口答计算结果:(x+a)(x+b)=x2+(a+b)x+ab (x+a)(x+b)=x2+(a+b)x+ab两个一次二项式相乘的积一个二次三项式整式的乘法反过来,得x2+(a+b)x+ab=(x+a)(x+b)一个二次三项式两个一次二项式相乘的积因式分解如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,而且一次项系数p又恰好是a+b,那么x2+px+q就可以进行如上的因式分解。
例一:步骤:①竖分二次项系数与常数项②交叉相乘,积相加③检验确定,横写因式十字相乘法(借助十字交叉线分解因式的方法)
试一试:小结:用十字相乘法把形如二次三项式分解因式使(顺口溜:竖分常数交叉验,横写因式不能乱。)(1)x2-7x+12 (2)x2-4x-12
(3)x2+8x+12 (4)x2-11x-12 解:(1)x2-7x+12 (2)x2-4x-12 -3+(-4)=-72+(-6)=-4(3)x2+8x+12 (4)x2-11x-12 2+6=81+(-12)=-11拓展:把 2x2-x-3 分解因式解:2x2-x-32+(-3)=-1十字相乘法的要领是:“头尾分解,交叉相乘,求和凑中,观察试验”.试一试:因式分解6x2-23x+106x2-23x+10解20+3=23对二次三项式x2+px+q用x2+(a+b)x+ab=(x+a)(x+b)进行因式分解,应重点掌握以下问题:2.掌握方法:拆分常数项,验证一次项.1.适用范围:只有当q=ab,且p=a+b时 才能用十字相乘法进行分解。慕联提示亲爱的同学,课后请做一个习题测试,假如达到90分以上,就说明你已经很好的掌握了这节课的内容,有关情况将记录在你的学习记录上,亲爱的同学再见!
下节课我们不见不散!
课程编号:TS1803010202R8114030301LWJ
慕课联盟课程开发中心:www.moocun.com阅读与思考:十字相乘法 1.理解十字相乘法的根据
2.能用十字相乘法分解二次三项式1.举例说明因式分解与整式乘法的关系2.我们已经学习了哪些因式分解的方法?
提公因式法: ma+mb+mc=m(a+b+c)
运用公式法: a2-b2=(a+b)(a-b)
a2 ±2ab+b2=(a ±b)21.(x+2)(x+1)=x2+3x+23.(x-2)(x+1)=x2-x-24.(x-2)(x-1)=x2-3x+22.(x+2)(x-1)=x2+x-25.(x+2)(x+3)=x2+5x+66.(x+2)(x-3)=x2-x-67.(x-2)(x+3)=x2+x-6(x+a)(x+b)=x2+(a+b)x+ab请直接口答计算结果:(x+a)(x+b)=x2+(a+b)x+ab (x+a)(x+b)=x2+(a+b)x+ab两个一次二项式相乘的积一个二次三项式整式的乘法反过来,得x2+(a+b)x+ab=(x+a)(x+b)一个二次三项式两个一次二项式相乘的积因式分解如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,而且一次项系数p又恰好是a+b,那么x2+px+q就可以进行如上的因式分解。
例一:步骤:①竖分二次项系数与常数项②交叉相乘,积相加③检验确定,横写因式十字相乘法(借助十字交叉线分解因式的方法)
试一试:小结:用十字相乘法把形如二次三项式分解因式使(顺口溜:竖分常数交叉验,横写因式不能乱。)(1)x2-7x+12 (2)x2-4x-12
(3)x2+8x+12 (4)x2-11x-12 解:(1)x2-7x+12 (2)x2-4x-12 -3+(-4)=-72+(-6)=-4(3)x2+8x+12 (4)x2-11x-12 2+6=81+(-12)=-11拓展:把 2x2-x-3 分解因式解:2x2-x-32+(-3)=-1十字相乘法的要领是:“头尾分解,交叉相乘,求和凑中,观察试验”.试一试:因式分解6x2-23x+106x2-23x+10解20+3=23对二次三项式x2+px+q用x2+(a+b)x+ab=(x+a)(x+b)进行因式分解,应重点掌握以下问题:2.掌握方法:拆分常数项,验证一次项.1.适用范围:只有当q=ab,且p=a+b时 才能用十字相乘法进行分解。慕联提示亲爱的同学,课后请做一个习题测试,假如达到90分以上,就说明你已经很好的掌握了这节课的内容,有关情况将记录在你的学习记录上,亲爱的同学再见!
下节课我们不见不散!
