高中数学必修一知识讲解,巩固练习(复习补习,期末复习资料):24【基础】《指数函数、对数函数、幂函数》全章复习与巩固
文档属性
| 名称 | 高中数学必修一知识讲解,巩固练习(复习补习,期末复习资料):24【基础】《指数函数、对数函数、幂函数》全章复习与巩固 |  | |
| 格式 | zip | ||
| 文件大小 | 528.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-12 22:21:35 | ||
图片预览



文档简介
指数函数、对数函数、幂函数综合
【学习目标】
1.理解有理指数幂的含义,掌握幂的运算.
2.理解指数函数的概念和意义,理解指数函数的单调性与特殊点.
3.理解对数的概念及其运算性质.
4.重点理解指数函数、对数函数、幂函数的性质,熟练掌握指数、对数运算法则,明确算理,能对常见的指数型函数、对数型函数进行变形处理.
5.会求以指数函数、对数函数、幂函数为载体的复合函数的定义域、单调性及值域等性质.
6.知道指数函数与对数函数互为反函数(a>0,a≠1).
【知识框图】
【要点梳理】
要点一:指数及指数幂的运算
1.根式的概念
的次方根的定义:一般地,如果,那么叫做的次方根,其中
当为奇数时,正数的次方根为正数,负数的次方根是负数,表示为;当为偶数时,正数的次方根有两个,这两个数互为相反数可以表示为.
负数没有偶次方根,0的任何次方根都是0.
式子叫做根式,叫做根指数,叫做被开方数.
2.n次方根的性质:
(1)当为奇数时,;当为偶数时,
(2)
3.分数指数幂的意义:
;
要点诠释:
0的正分数指数幂等于0,负分数指数幂没有意义.
4.有理数指数幂的运算性质:
(1) (2) (3)
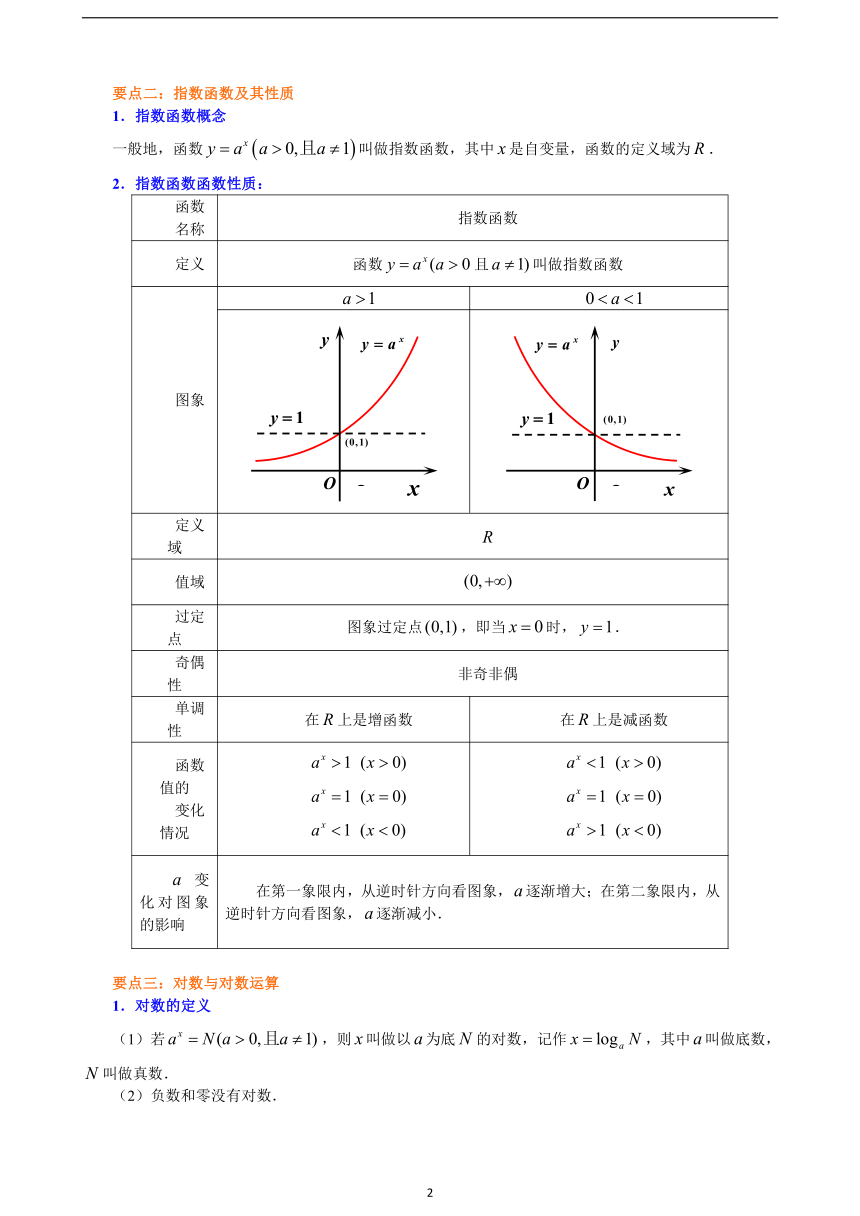
要点二:指数函数及其性质
1.指数函数概念
一般地,函数叫做指数函数,其中是自变量,函数的定义域为.
2.指数函数函数性质:
函数
名称
指数函数
定义
函数且叫做指数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的
变化情况
变化对图象的影响
在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小.
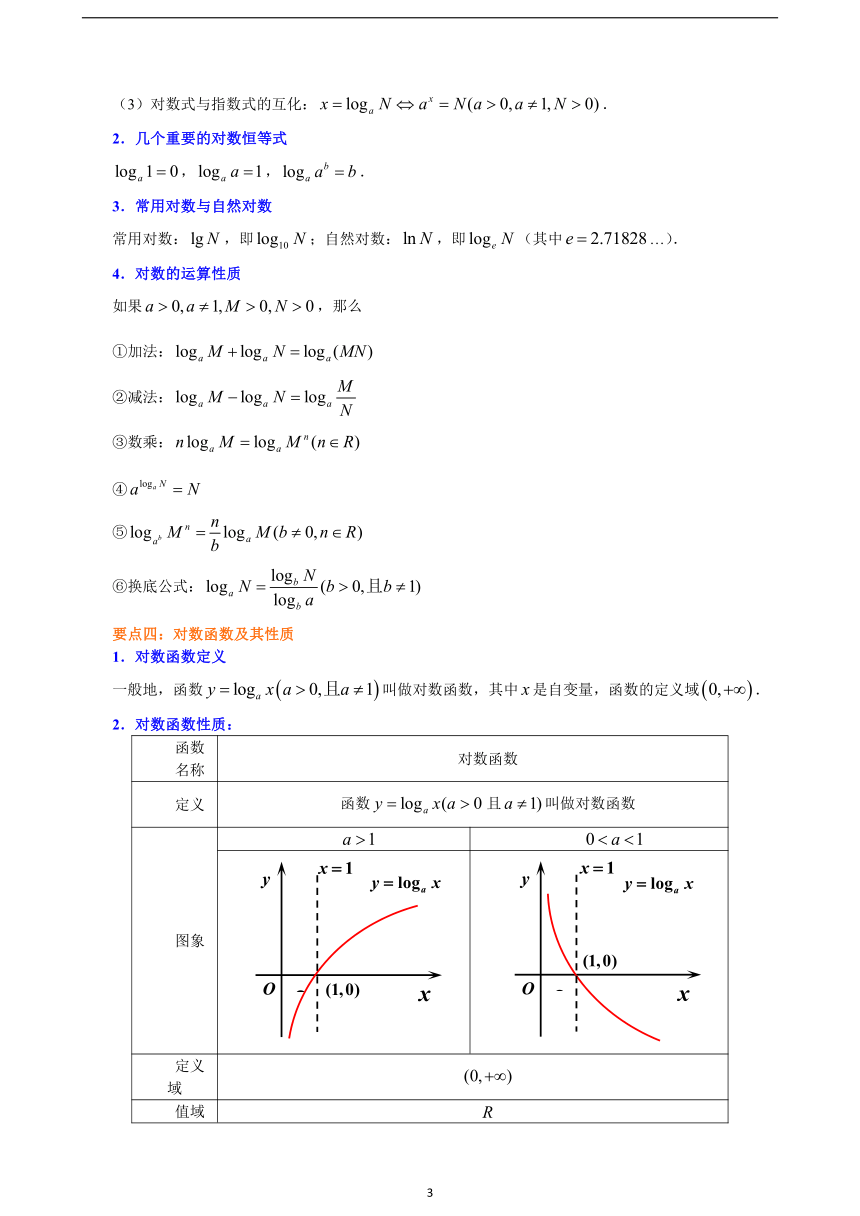
要点三:对数与对数运算
1.对数的定义
(1)若,则叫做以为底的对数,记作,其中叫做底数,叫做真数.
(2)负数和零没有对数.
(3)对数式与指数式的互化:.
2.几个重要的对数恒等式
,,.
3.常用对数与自然对数
常用对数:,即;自然对数:,即(其中…).
4.对数的运算性质
如果,那么
①加法:
②减法:
③数乘:
④
⑤
⑥换底公式:
要点四:对数函数及其性质
1.对数函数定义
一般地,函数叫做对数函数,其中是自变量,函数的定义域.
2.对数函数性质:
函数
名称
对数函数
定义
函数且叫做对数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的
变化情况
变化对图象的影响
在第一象限内,从顺时针方向看图象,逐渐增大;在第四象限内,从顺时针方向看图象,逐渐减小.
要点五:反函数
1.反函数的概念
设函数的定义域为,值域为,从式子中解出,得式子.如果对于在中的任何一个值,通过式子,在中都有唯一确定的值和它对应,那么式子表示是的函数,函数叫做函数的反函数,记作,习惯上改写成.
2.反函数的性质
(1)原函数与反函数的图象关于直线对称.
(2)函数的定义域、值域分别是其反函数的值域、定义域.
(3)若在原函数的图象上,则在反函数的图象上.
(4)一般地,函数要有反函数则它必须为单调函数.
要点六:幂函数
1.幂函数概念
形如的函数,叫做幂函数,其中为常数.
2.幂函数的性质
(1)图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.
(2)过定点:所有的幂函数在都有定义,并且图象都通过点.
(3)单调性:如果,则幂函数的图象过原点,并且在上为增函数.如果,则幂函数的图象在上为减函数,在第一象限内,图象无限接近轴与轴.
【典型例题】
类型一:指数、对数运算
例1.化简与计算下列各式
(1);
(2);
(3).
【思路点拨】运算时尽量把根式转化为分数指数幂,而小数也要化为分数为好.
【答案】(1);(2)100;(3).
【解析】
(1)原式=
=1+=;
(2)原式=
=
=100
(3) 原式=
.
【总结升华】化简要求同初中要求,注意结果形式的统一,结果不能同时含有根式和分数指数,也不能既有分母又含有负指数;一般地,进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数位分数等,便于进行乘、除、乘方、开方运算,以达到化繁为简的目的;
举一反三:
【变式一】化简下列各式:
(1); (2).
【答案】(1)-27;(2).
【解析】(1)
;
(2)
.
例2.已知:,求:的值.
【思路点拨】先化简再求值是解决此类问题的一般方法.
【答案】2
【解析】
∴ 当时,.
【总结升华】解题时观察已知与所求之间的关系,同时乘法公式要熟练,直接代入条件求解繁琐,故应先化简变形,创造条件简化运算. 解题时,要注意运用下列各式.,;
例3.计算
(1) ; (2);
(3).
【答案】(1);(2)1;(3)3;(4)14.
【解析】(1)原式=;
(2)原式=
=
=1-+=1
(3)原式=
=
=2+=3;
【总结升华】这是一组很基本的对数运算的练习题,虽然在考试中这些运算要求并不高,但是数式运算是学习数学的基本功,通过这样的运算练习熟练掌握运算公式、法则,以及学习数式变换的各种技巧.
【变式1】=( )
A.0 B.1 C.2 D.4
【答案】C
【解析】=.
【变式2】(1);(2).
【答案】(1)2;(2).
【解析】(1) 原式
;
(2) 原式
.
类型二:指数函数、对数函数、幂函数的图象与性质
4.(2017年山东高考)设函数,若,则b=( )
A.1 B. C. D.
【答案】D
【解析】由题意,由得,
或,解得,故选D.
【总结升华】利用指数函数、对数函数的概念,求解函数的值.
举一反三:
【变式1】已知函数若,则实数等于( ).
A. B. C. 2 D. 9
【答案】.
【解析】,由,则有.,,选.
例5.(2018 湖南岳阳模拟)若函数y=f(x)的定义域是[2,4],则的定义域是( )
A. B.[4,16] C. D.[2,4]
【思路点拨】令,使t满足y=f(x)的定义域中x的取值范围相同,求出的定义域即可.
【答案】C
【解析】∵,令,
∴,
∵函数y=f(x)的定义域是[2,4],
∴y=f(t)的定义域也为[2,4],即2≤t≤4,
∴有,解得:,
∵函数的定义域即解析式中自变量的取值范围,
∴的定义域为,
即:.
故选C.
【总结升华】本题只要明确函数的定义域即解析式中自变量的取值范围,运用整体代换(换元法)即可迎刃而解.
例6.函数的图象是( )
A. B. C. D.
【答案】B
【解析】先作出的图象,然后作出这个图象关于轴对称的图象,得到的图象,再把的图象右移一个单位,得到的图象,故选B
例7. 函数的单调递增区间是( )
A.(3,+∞) B.(-∞,3) C.(4,+∞) D.(-∞,2)
【思路点拨】这是一个内层函数是二次函数,外层函数是对数函数的复合函数,其单调性由这两个函数的单调性共同决定,即“同增异减”。
【答案】D
【解析】函数是由复合而成的,是减函数,在上单调递增,在上单调递减,由对数函数的真数必须大于零,即,解得或,所以原函数的单调递增区间是,故选D.
类型三:综合问题
例8.已知函数为常数)
(1)求函数f(x)的定义域;
(2)若a=2,试根据单调性定义确定函数f(x)的单调性.
(3)若函数y=f(x)是增函数,求a的取值范围.
【思路点拨】(1)利用真数大于零求解(2)利用定义去证明函数的单调性
【答案】(1);(2)f(x)为增函数;(3)a>1.
【解析】(1)由
∵a>0,x≥0
∴f(x)的定义域是.
(2)若a=2,则
设 , 则
故f(x)为增函数.
(3)设
①
∵f(x)是增函数,
∴f(x1)>f(x2)
即 ②
联立①、②知a>1,
∴a∈(1,+∞).
【总结升华】该题属于纯粹的研究复合对函数性质的问题,我们抓住对数函数的特点,结合一般函数求定义域、单调性的解题思路,对“路”处理即可.
举一反三:
【变式1】(2017北京高考真题)设函数
①若a=1,则f(x)的最小值为___________;
②若f(x)恰有2个零点,则实数a的取值范围是_________.
【答案】-1;
【解析】①a=1时,函数f(x)在上为增函数,函数值大于1;在为减函数,在为增函数,当时,f(x)取得最小值为-1;
② i)若函数在x<1时与x轴有一个交点,
所以a>0,并且当x=1时,h(1)=2-a>0,所以0<a<2,
函数g(x)=4(x-a)(x-2a)有一个交点,所以2a≥1且a<1
所以
ii)若函数h(x)=2x-a与x轴没有交点,
则函数g(x)=4(x-a)(x-2a)与x轴有两个交点.
当a≤0,h(x)与x轴无交点,g(x)在x≥1时与x轴无交点,不满足题意(舍)
当h(1)=2-a≥0时,a≥2,
g(x)与x轴有两个交点为x1=a,x2=2a都满足题意
综上所述,a的取值范围是或a≥2.
故答案为:-1;
【巩固练习】
1.下列函数与有相同图象的一个函数是( )
A. B.
C. D.
2.函数与的图象关于下列那种图形对称( )
A.轴 B.轴 C.直线 D.原点中心对称
3.(2017年山东高考)若函数是奇函数,则使f(x)>3成立的x的取值范围为( )
A.(-∞,-1) B.(-1,0) C.(0,1) D.(1,+∞)
4.函数在上递减,那么在上( )
A.递增且无最大值 B.递减且无最小值
C.递增且有最大值 D.递减且有最小值
5.为了得到函数的图象,只需把函数的图象上所有的点( )
A.向左平移3个单位长度,再向上平移1个单位长度;
B.向右平移3个单位长度,再向上平移1个单位长度;
C.向左平移3个单位长度,再向下平移1个单位长度;
D.向右平移3个单位长度,再向下平移1个单位长度;
6.函数的定义域为( );
A. B.
C. D.
7.当0A.(0,) B.(,1) C.(1,) D.(,2)
8.函数的反函数是( )
A. B.
C. D.
9.(2018春 上海月考)已知,若f(a)>f(2),则a的取值范围是________.
10.已知函数,对任意都有,则、 、的大小顺序是 .
11.函数的定义域是 ;值域是 .
12.函数的定义域是 .
13.(2018春 广东揭阳月考)已知函数,其中a>0且a≠1.
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性,并说明理由;
(3),求使f(x)>0成立的x的集合.
14.(1)求函数的定义域;
(2)求函数的值域.
15.已知,求函数的值域.
【答案与解析】
1.【答案】D
【解析】 ,对应法则不同;
;.
2.【答案】D
【解析】由得,即关于原点对称.
3.【答案】C
【解析】由题意f(x)=―f(―x),即所以,,a=1,,由得,,0<x<1,故选C.
4.【答案】A
【解析】令,是的递减区间,即,是的递增区间,即递增且无最大值.
5.【答案】C
【解析】=,只需将的图象上所有点向左平移3个单位长度,向下平移1个单位长度,即可得要求的图象.
6.【答案】D
【解析】.
故选D.
7.【答案】B
【解析】,,又当时, ,所以,即,所以综上得:的取值范围为.
8.【答案】D
【解析】由,解得即,故所求反函数为,故选D.
9.【答案】
【解析】∵,
∴函数在(0,1)上单调递减,在(1,+∞)上单调递增
若f(a)>f(2),则,或a>2,
∴满足条件的a的取值范围为
故答案为:
10.【答案】
【解析】因为,所以函数的对称轴为,又函数的开口向上,所以有离对称轴越远,函数值越大,所以
11.【答案】
【解析】 ;.
12.【答案】[1,2)
【解析】函数定义域要满足,即,
解得1≤x<2,即函数的定义域为[1,2),
故答案为:[1,2)
点评:本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.
13.【答案】(1)(-1,1);(2)f(x)是奇函数;(3)(0,1)
【解析】(1)要使函数有意义,则,
解得-1<x<1,
即函数f(x)的定义域为(-1,1);
(2)∵,
∴f(x)是奇函数.
(3)若,
∴,
解得:a=2,
∴ ,
若f(x)>0,则,
∴x+1>1-x>0,
解得0<x<1,
故不等式的解集为(0,1).
14.【答案】(1)(2)
【解析】(1),即定义域为;
(2)令,则,,即值域为.
15.【答案】
【解析】,令则,,即时,取得最大值12;当,即时,取得最小值-24,即的最大值为12,最小值为-24,所以函数的值域为.
【学习目标】
1.理解有理指数幂的含义,掌握幂的运算.
2.理解指数函数的概念和意义,理解指数函数的单调性与特殊点.
3.理解对数的概念及其运算性质.
4.重点理解指数函数、对数函数、幂函数的性质,熟练掌握指数、对数运算法则,明确算理,能对常见的指数型函数、对数型函数进行变形处理.
5.会求以指数函数、对数函数、幂函数为载体的复合函数的定义域、单调性及值域等性质.
6.知道指数函数与对数函数互为反函数(a>0,a≠1).
【知识框图】
【要点梳理】
要点一:指数及指数幂的运算
1.根式的概念
的次方根的定义:一般地,如果,那么叫做的次方根,其中
当为奇数时,正数的次方根为正数,负数的次方根是负数,表示为;当为偶数时,正数的次方根有两个,这两个数互为相反数可以表示为.
负数没有偶次方根,0的任何次方根都是0.
式子叫做根式,叫做根指数,叫做被开方数.
2.n次方根的性质:
(1)当为奇数时,;当为偶数时,
(2)
3.分数指数幂的意义:
;
要点诠释:
0的正分数指数幂等于0,负分数指数幂没有意义.
4.有理数指数幂的运算性质:
(1) (2) (3)
要点二:指数函数及其性质
1.指数函数概念
一般地,函数叫做指数函数,其中是自变量,函数的定义域为.
2.指数函数函数性质:
函数
名称
指数函数
定义
函数且叫做指数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的
变化情况
变化对图象的影响
在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小.
要点三:对数与对数运算
1.对数的定义
(1)若,则叫做以为底的对数,记作,其中叫做底数,叫做真数.
(2)负数和零没有对数.
(3)对数式与指数式的互化:.
2.几个重要的对数恒等式
,,.
3.常用对数与自然对数
常用对数:,即;自然对数:,即(其中…).
4.对数的运算性质
如果,那么
①加法:
②减法:
③数乘:
④
⑤
⑥换底公式:
要点四:对数函数及其性质
1.对数函数定义
一般地,函数叫做对数函数,其中是自变量,函数的定义域.
2.对数函数性质:
函数
名称
对数函数
定义
函数且叫做对数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的
变化情况
变化对图象的影响
在第一象限内,从顺时针方向看图象,逐渐增大;在第四象限内,从顺时针方向看图象,逐渐减小.
要点五:反函数
1.反函数的概念
设函数的定义域为,值域为,从式子中解出,得式子.如果对于在中的任何一个值,通过式子,在中都有唯一确定的值和它对应,那么式子表示是的函数,函数叫做函数的反函数,记作,习惯上改写成.
2.反函数的性质
(1)原函数与反函数的图象关于直线对称.
(2)函数的定义域、值域分别是其反函数的值域、定义域.
(3)若在原函数的图象上,则在反函数的图象上.
(4)一般地,函数要有反函数则它必须为单调函数.
要点六:幂函数
1.幂函数概念
形如的函数,叫做幂函数,其中为常数.
2.幂函数的性质
(1)图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.
(2)过定点:所有的幂函数在都有定义,并且图象都通过点.
(3)单调性:如果,则幂函数的图象过原点,并且在上为增函数.如果,则幂函数的图象在上为减函数,在第一象限内,图象无限接近轴与轴.
【典型例题】
类型一:指数、对数运算
例1.化简与计算下列各式
(1);
(2);
(3).
【思路点拨】运算时尽量把根式转化为分数指数幂,而小数也要化为分数为好.
【答案】(1);(2)100;(3).
【解析】
(1)原式=
=1+=;
(2)原式=
=
=100
(3) 原式=
.
【总结升华】化简要求同初中要求,注意结果形式的统一,结果不能同时含有根式和分数指数,也不能既有分母又含有负指数;一般地,进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数位分数等,便于进行乘、除、乘方、开方运算,以达到化繁为简的目的;
举一反三:
【变式一】化简下列各式:
(1); (2).
【答案】(1)-27;(2).
【解析】(1)
;
(2)
.
例2.已知:,求:的值.
【思路点拨】先化简再求值是解决此类问题的一般方法.
【答案】2
【解析】
∴ 当时,.
【总结升华】解题时观察已知与所求之间的关系,同时乘法公式要熟练,直接代入条件求解繁琐,故应先化简变形,创造条件简化运算. 解题时,要注意运用下列各式.,;
例3.计算
(1) ; (2);
(3).
【答案】(1);(2)1;(3)3;(4)14.
【解析】(1)原式=;
(2)原式=
=
=1-+=1
(3)原式=
=
=2+=3;
【总结升华】这是一组很基本的对数运算的练习题,虽然在考试中这些运算要求并不高,但是数式运算是学习数学的基本功,通过这样的运算练习熟练掌握运算公式、法则,以及学习数式变换的各种技巧.
【变式1】=( )
A.0 B.1 C.2 D.4
【答案】C
【解析】=.
【变式2】(1);(2).
【答案】(1)2;(2).
【解析】(1) 原式
;
(2) 原式
.
类型二:指数函数、对数函数、幂函数的图象与性质
4.(2017年山东高考)设函数,若,则b=( )
A.1 B. C. D.
【答案】D
【解析】由题意,由得,
或,解得,故选D.
【总结升华】利用指数函数、对数函数的概念,求解函数的值.
举一反三:
【变式1】已知函数若,则实数等于( ).
A. B. C. 2 D. 9
【答案】.
【解析】,由,则有.,,选.
例5.(2018 湖南岳阳模拟)若函数y=f(x)的定义域是[2,4],则的定义域是( )
A. B.[4,16] C. D.[2,4]
【思路点拨】令,使t满足y=f(x)的定义域中x的取值范围相同,求出的定义域即可.
【答案】C
【解析】∵,令,
∴,
∵函数y=f(x)的定义域是[2,4],
∴y=f(t)的定义域也为[2,4],即2≤t≤4,
∴有,解得:,
∵函数的定义域即解析式中自变量的取值范围,
∴的定义域为,
即:.
故选C.
【总结升华】本题只要明确函数的定义域即解析式中自变量的取值范围,运用整体代换(换元法)即可迎刃而解.
例6.函数的图象是( )
A. B. C. D.
【答案】B
【解析】先作出的图象,然后作出这个图象关于轴对称的图象,得到的图象,再把的图象右移一个单位,得到的图象,故选B
例7. 函数的单调递增区间是( )
A.(3,+∞) B.(-∞,3) C.(4,+∞) D.(-∞,2)
【思路点拨】这是一个内层函数是二次函数,外层函数是对数函数的复合函数,其单调性由这两个函数的单调性共同决定,即“同增异减”。
【答案】D
【解析】函数是由复合而成的,是减函数,在上单调递增,在上单调递减,由对数函数的真数必须大于零,即,解得或,所以原函数的单调递增区间是,故选D.
类型三:综合问题
例8.已知函数为常数)
(1)求函数f(x)的定义域;
(2)若a=2,试根据单调性定义确定函数f(x)的单调性.
(3)若函数y=f(x)是增函数,求a的取值范围.
【思路点拨】(1)利用真数大于零求解(2)利用定义去证明函数的单调性
【答案】(1);(2)f(x)为增函数;(3)a>1.
【解析】(1)由
∵a>0,x≥0
∴f(x)的定义域是.
(2)若a=2,则
设 , 则
故f(x)为增函数.
(3)设
①
∵f(x)是增函数,
∴f(x1)>f(x2)
即 ②
联立①、②知a>1,
∴a∈(1,+∞).
【总结升华】该题属于纯粹的研究复合对函数性质的问题,我们抓住对数函数的特点,结合一般函数求定义域、单调性的解题思路,对“路”处理即可.
举一反三:
【变式1】(2017北京高考真题)设函数
①若a=1,则f(x)的最小值为___________;
②若f(x)恰有2个零点,则实数a的取值范围是_________.
【答案】-1;
【解析】①a=1时,函数f(x)在上为增函数,函数值大于1;在为减函数,在为增函数,当时,f(x)取得最小值为-1;
② i)若函数在x<1时与x轴有一个交点,
所以a>0,并且当x=1时,h(1)=2-a>0,所以0<a<2,
函数g(x)=4(x-a)(x-2a)有一个交点,所以2a≥1且a<1
所以
ii)若函数h(x)=2x-a与x轴没有交点,
则函数g(x)=4(x-a)(x-2a)与x轴有两个交点.
当a≤0,h(x)与x轴无交点,g(x)在x≥1时与x轴无交点,不满足题意(舍)
当h(1)=2-a≥0时,a≥2,
g(x)与x轴有两个交点为x1=a,x2=2a都满足题意
综上所述,a的取值范围是或a≥2.
故答案为:-1;
【巩固练习】
1.下列函数与有相同图象的一个函数是( )
A. B.
C. D.
2.函数与的图象关于下列那种图形对称( )
A.轴 B.轴 C.直线 D.原点中心对称
3.(2017年山东高考)若函数是奇函数,则使f(x)>3成立的x的取值范围为( )
A.(-∞,-1) B.(-1,0) C.(0,1) D.(1,+∞)
4.函数在上递减,那么在上( )
A.递增且无最大值 B.递减且无最小值
C.递增且有最大值 D.递减且有最小值
5.为了得到函数的图象,只需把函数的图象上所有的点( )
A.向左平移3个单位长度,再向上平移1个单位长度;
B.向右平移3个单位长度,再向上平移1个单位长度;
C.向左平移3个单位长度,再向下平移1个单位长度;
D.向右平移3个单位长度,再向下平移1个单位长度;
6.函数的定义域为( );
A. B.
C. D.
7.当0
8.函数的反函数是( )
A. B.
C. D.
9.(2018春 上海月考)已知,若f(a)>f(2),则a的取值范围是________.
10.已知函数,对任意都有,则、 、的大小顺序是 .
11.函数的定义域是 ;值域是 .
12.函数的定义域是 .
13.(2018春 广东揭阳月考)已知函数,其中a>0且a≠1.
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性,并说明理由;
(3),求使f(x)>0成立的x的集合.
14.(1)求函数的定义域;
(2)求函数的值域.
15.已知,求函数的值域.
【答案与解析】
1.【答案】D
【解析】 ,对应法则不同;
;.
2.【答案】D
【解析】由得,即关于原点对称.
3.【答案】C
【解析】由题意f(x)=―f(―x),即所以,,a=1,,由得,,0<x<1,故选C.
4.【答案】A
【解析】令,是的递减区间,即,是的递增区间,即递增且无最大值.
5.【答案】C
【解析】=,只需将的图象上所有点向左平移3个单位长度,向下平移1个单位长度,即可得要求的图象.
6.【答案】D
【解析】.
故选D.
7.【答案】B
【解析】,,又当时, ,所以,即,所以综上得:的取值范围为.
8.【答案】D
【解析】由,解得即,故所求反函数为,故选D.
9.【答案】
【解析】∵,
∴函数在(0,1)上单调递减,在(1,+∞)上单调递增
若f(a)>f(2),则,或a>2,
∴满足条件的a的取值范围为
故答案为:
10.【答案】
【解析】因为,所以函数的对称轴为,又函数的开口向上,所以有离对称轴越远,函数值越大,所以
11.【答案】
【解析】 ;.
12.【答案】[1,2)
【解析】函数定义域要满足,即,
解得1≤x<2,即函数的定义域为[1,2),
故答案为:[1,2)
点评:本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.
13.【答案】(1)(-1,1);(2)f(x)是奇函数;(3)(0,1)
【解析】(1)要使函数有意义,则,
解得-1<x<1,
即函数f(x)的定义域为(-1,1);
(2)∵,
∴f(x)是奇函数.
(3)若,
∴,
解得:a=2,
∴ ,
若f(x)>0,则,
∴x+1>1-x>0,
解得0<x<1,
故不等式的解集为(0,1).
14.【答案】(1)(2)
【解析】(1),即定义域为;
(2)令,则,,即值域为.
15.【答案】
【解析】,令则,,即时,取得最大值12;当,即时,取得最小值-24,即的最大值为12,最小值为-24,所以函数的值域为.
