高中数学必修一知识讲解,巩固练习(复习补习,期末复习资料):25【提高】《指数函数、对数函数、幂函数》全章复习与巩固
文档属性
| 名称 | 高中数学必修一知识讲解,巩固练习(复习补习,期末复习资料):25【提高】《指数函数、对数函数、幂函数》全章复习与巩固 |

|
|
| 格式 | zip | ||
| 文件大小 | 749.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-12 00:00:00 | ||
图片预览



文档简介
指数函数、对数函数、幂函数综合
【学习目标】
1.理解有理指数幂的含义,掌握幂的运算.
2.理解指数函数的概念和意义,理解指数函数的单调性与特殊点.
3.理解对数的概念及其运算性质.
4.重点理解指数函数、对数函数、幂函数的性质,熟练掌握指数、对数运算法则,明确算理,能对常见的指数型函数、对数型函数进行变形处理.
5.会求以指数函数、对数函数、幂函数为载体的复合函数的定义域、单调性及值域等性质.
6.知道指数函数与对数函数互为反函数(a>0,a≠1).
【知识框图】
/
【要点梳理】
要点一:指数及指数幂的运算
1.根式的概念
的次方根的定义:一般地,如果,那么叫做的次方根,其中
当为奇数时,正数的次方根为正数,负数的次方根是负数,表示为;当为偶数时,正数的次方根有两个,这两个数互为相反数可以表示为.
负数没有偶次方根,0的任何次方根都是0.
式子叫做根式,叫做根指数,叫做被开方数.
2.n次方根的性质:
(1)当为奇数时,;当为偶数时,
(2)
3.分数指数幂的意义:
;
要点诠释:
0的正分数指数幂等于0,负分数指数幂没有意义.
4.有理数指数幂的运算性质:
(1) (2) (3)
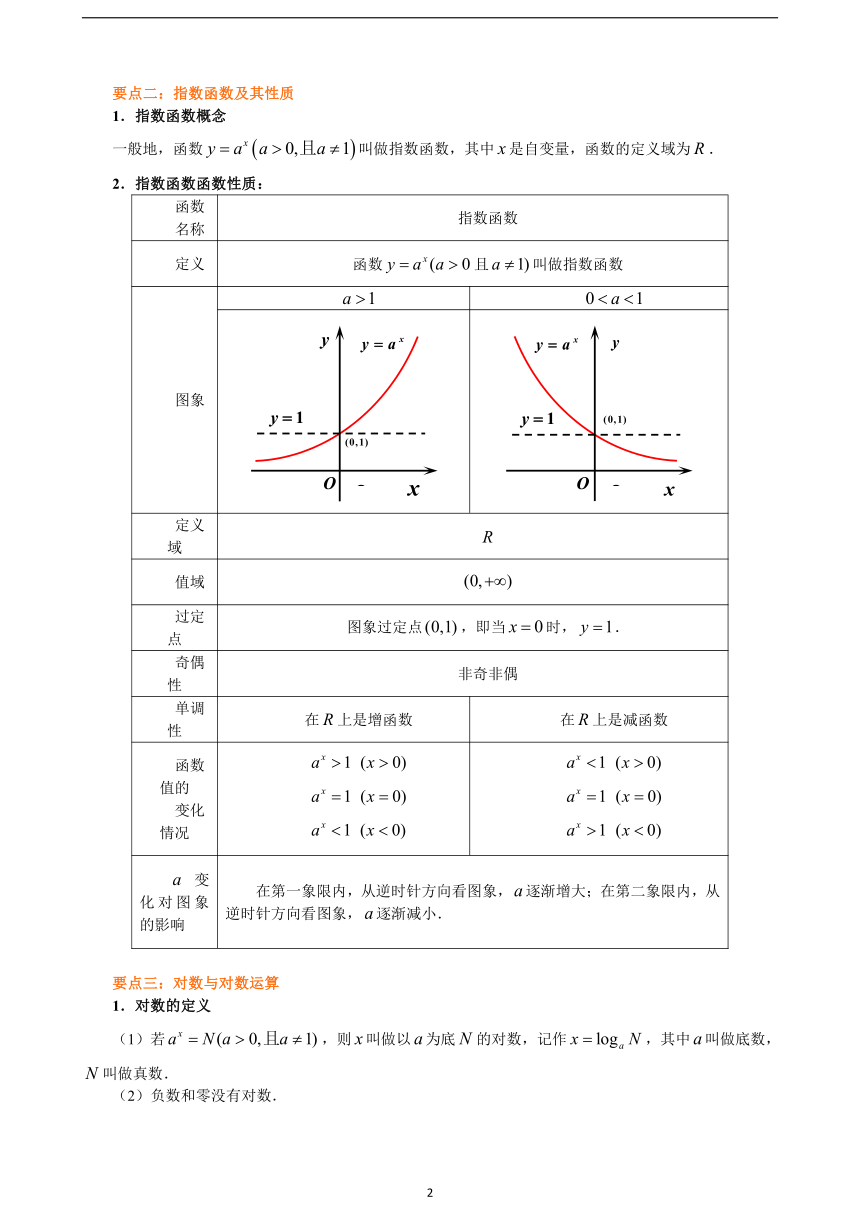
要点二:指数函数及其性质
1.指数函数概念
一般地,函数叫做指数函数,其中是自变量,函数的定义域为.
2.指数函数函数性质:
函数
名称
指数函数
定义
函数且叫做指数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的
变化情况
变化对图象的影响
在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小.
要点三:对数与对数运算
1.对数的定义
(1)若,则叫做以为底的对数,记作,其中叫做底数,叫做真数.
(2)负数和零没有对数.
(3)对数式与指数式的互化:.
2.几个重要的对数恒等式
,,.
3.常用对数与自然对数
常用对数:,即;自然对数:,即(其中…).
4.对数的运算性质
如果,那么
①加法:
②减法:
③数乘:
④
⑤
⑥换底公式:
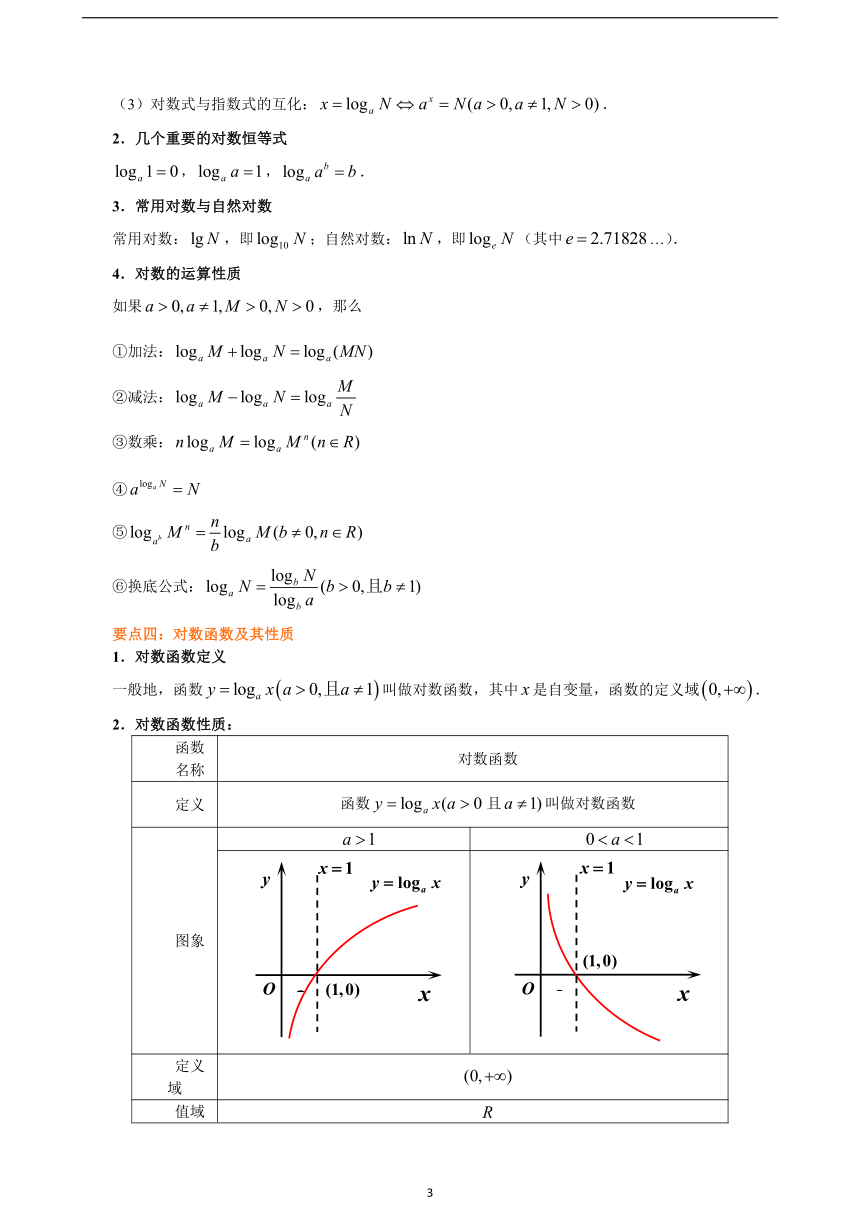
要点四:对数函数及其性质
1.对数函数定义
一般地,函数叫做对数函数,其中是自变量,函数的定义域.
2.对数函数性质:
函数
名称
对数函数
定义
函数且叫做对数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的
变化情况
变化对图象的影响
在第一象限内,从顺时针方向看图象,逐渐增大;在第四象限内,从顺时针方向看图象,逐渐减小.
要点五:反函数
1.反函数的概念
设函数的定义域为,值域为,从式子中解出,得式子.如果对于在中的任何一个值,通过式子,在中都有唯一确定的值和它对应,那么式子表示是的函数,函数叫做函数的反函数,记作,习惯上改写成.
2.反函数的性质
(1)原函数与反函数的图象关于直线对称.
(2)函数的定义域、值域分别是其反函数的值域、定义域.
(3)若在原函数的图象上,则在反函数的图象上.
(4)一般地,函数要有反函数则它必须为单调函数.
要点六:幂函数
1.幂函数概念
形如/的函数,叫做幂函数,其中为常数.
2.幂函数的性质
(1)图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.
(2)过定点:所有的幂函数在都有定义,并且图象都通过点.
(3)单调性:如果,则幂函数的图象过原点,并且在上为增函数.如果,则幂函数的图象在上为减函数,在第一象限内,图象无限接近轴与轴.
(4)奇偶性:当为奇数时,幂函数为奇函数,当为偶数时,幂函数为偶函数.当(其中互质,和),若为奇数为奇数时,则是奇函数,若为奇数为偶数时,则是偶函数,若为偶数为奇数时,则是非奇非偶函数.
(5)图象特征:幂函数,当时,若,其图象在直线下方,若,其图象在直线上方,当时,若,其图象在直线上方,若,其图象在直线下方.
【典型例题】
类型一:指数、对数运算
例1.计算
(1) ; (2);
(3);(4)
【思路点拨】运算时尽量把根式转化为分数指数幂,而小数也要化为分数为好.
【答案】(1);(2)1;(3)3;(4)14.
【解析】(1)原式=;
(2)原式=
=
=1-+=1
(3)原式=
=
=2+=3;
(4)令,两边取常用对数得
=
=
=
即=14.
【总结升华】这是一组很基本的对数运算的练习题,虽然在考试中这些运算要求并不高,但是数式运算是学习数学的基本功,通过这样的运算练习熟练掌握运算公式、法则,以及学习数式变换的各种技巧.
举一反三:
【变式1】=( )
A.0 B.1 C.2 D.4
【答案】C
【解析】=.
【变式2】(1);(2).
【答案】(1)2;(2).
【解析】(1) 原式
;
(2) 原式
.
类型二:指数函数、对数函数、幂函数的图象与性质
例2.设偶函数满足,则= ( )
A. B.
C. D.
【答案】 B
【解析】且是偶函数.
或
或
解得或,故选B.
【总结升华】考查解不等式组及函数解析式,考查函数性质的综合运用.
举一反三:
【变式1】已知函数若,则的取值范围是( ).
A. B. 或 C. D. 或
【答案】A
【解析】依题意或即或,所以,故选A.
例3.设函数 若,则实数的取值范围是( ) .
A. B.
C. D.
【答案】C
【解析】解法一:①若,则,
,得,得,解得.
②若则,
,
解得
由①②可知
解法二:特殊值验证
令
,满足,故排除A、D.
令,,
不满足,故排除B.
【总结升华】本题考查了分段函数的性质、分类思想的应用.
例4.函数的单调递增区间是( )
A.(3,+∞) B.(-∞,3) C.(4,+∞) D.(-∞,2)
【思路点拨】这是一个内层函数是二次函数,外层函数是对数函数的复合函数,其单调性由这两个函数的单调性共同决定,即“同增异减”.
【答案】D
【解析】函数是由复合而成的,是减函数,在上单调递增,在上单调递减,由对数函数的真数必须大于零,即,解得或,所以原函数的单调递增区间是,故选D.
例5.(2018 上海模拟)已知函数(a>0,a≠1)在区间[―1,2]上的最大值为8,最小值为m.若函数是单调增函数,则a=________.
【思路点拨】根据题意求出m的取值范围,再讨论a的值,求出f(x)的单调性,从而求出a的值.
【答案】
【解析】根据题意,得3-10m>0,
解得;
当a>1时,函数在区间[-1,2]上单调递增,最大值为,解得,最小值为,不合题意,舍去;
当1>a>0时,函数在区间[―1,2]上单调递减,最大值为,解得,最小值为,满足题意;
综上,.
故答案为:.
【总结升华】本题主要考查指数函数的图象与性质的应用问题,通过讨论对数函数的底数确定函数的单调性是解决本题的关键.
举一反三:
【变式1】已知,该函数在区间[a,b]上的值域为[1,2],记满足该条件的实数a、b所形成的实数对为点P(a,b),则由点P构成的点集组成的图形为( )
A. 线段AD B. 线段AB
C. 线段AD与线段CD D. 线段AB与BC
【思路点拨】由指数函数的图象和性质,我们易构造出满足条件函数在闭区间[a,b]上的值域为[1,2]的不等式组,画出函数的图象后与答案进行比照,即可得到答案.
【答案】C
【解析】∵函数的图象为开口方向朝上,以x=1为对称轴的曲线,如图.
当x=1时,函数取最小值1,
若,则x=0,或x=1
而函数|在闭区间[a,b]上的值域为[1,2],
则或,
则有序实数对(a,b)在坐标平面内所对应点组成图形为
/
故选C.
【总结升华】本题考查的知识点是指数函数的性质,函数的值域,其中熟练掌指数函数在定区间上的值域问题,将已知转化为关于a,b的不等式组,是解答本题的关键.
【变式2】已知函数若互不相等,且,则的取值范围是( ).
A.(1,10) B.(5,6) C.(10,12) D.(20,24)
【答案】C
【解析】由互不相等,结合图象可知:这三个数分别在区间(0,1),(1,10),(10,12)上,不妨设,由得即,所以,所以,故选C.
【总结升华】考查利用图象求解的能力和对数的运算,考查数形结合的思想方法.
类型三:综合问题
例6.已知定义域为的函数是奇函数。
(Ⅰ)求的值;
(Ⅱ)若对任意的,不等式恒成立,求的取值范围
【思路点拨】(Ⅰ)利用奇函数的定义去解。(Ⅱ)先判断函数的单调性,由单调性脱掉函数符号,转化成二次函数问题去解决。
【答案】(Ⅰ),;(Ⅱ)
【解析】(Ⅰ)因为是奇函数,所以=0,即
又由f(1)=-f(-1)知
(Ⅱ)解法一:由(Ⅰ)知,易知在上
为减函数。又因是奇函数,从而不等式:
等价于=,因为减函数,由上式推得:
即对一切有:,
从而判别式
(或: 即对一切有:,又
∴
解法二:由(Ⅰ)知.又由题设条件得:
,
即 :,
整理得 ,因底数,故:
上式对一切均成立,从而判别式
【总结升华】对于含指数式、对数式等式的形式,解题思路是转化为不含指数、对数因式的普通等式或方程的形式,再来求解.
举一反三:
【变式1】已知函数,(a>0,且a≠1).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并说明理由;
(3)设,解不等式f(x)>0.
【解析】(1)依题意知,解得
函数f(x)的定义域为.
(2)函数是奇函数
任取,,所以
=0
所以函数是奇函数.
(3)因为,所以
由,得
解得
.
例7.设(其中a为实数),如果当时恒有成立,求实数a的取值范围.
【思路点拨】由题意知,原不等式转化成在上恒成立,只要求出不等式右边部分的最大值就可以了.
【答案】
【解析】依题意,在上恒成立.
则设
只需求的最大值
任取且
=
由于是单调递减函数
,即在上是单调递增的,
【总结升华】解决本题的关键是把转化成,转化成,这种问题以后还会碰到,希望同学们多注意.
举一反三:
【变式1】设函数.
(1)求的定义域;
(2)求使在上恒成立的实数的取值范围.
【解析】(1),即
若,则的定义域为;
若,则的定义域为;
若,则的定义域为.
(2)①当时,在的定义域内,等价于,即,于是问题等价于在上恒成立.
令,则在上递减,在上递增,,即.
另一方面要使在上恒成立,则必是定义域的子集,由(1)可知
由且可知.
②当时,在的定义域内,等价于,于是问题等价于在上恒成立.
显然这样的实数不存在.
综上所求的的取值范围为.
【巩固练习】
1.若函数在区间上的最大值是最小值的倍,则的值为( )
A. B. C. D.
2.设函数f(x)=/则满足的的取值范围是( )
A. B. C. D.
3.函数在上递减,那么在上( )
A.递增且无最大值 B.递减且无最小值
C.递增且有最大值 D.递减且有最小值
4.若函数(a>0,a≠1)为增函数,那么的图象是( )
/ / / /
A. B. C. D.
5.函数的定义域为( );
A. B.
C. D.
6.已知是[0,1]上的减函数,则a的取值范围为( )
A. (0,1) B. (1,2) C. (0,2) D. [2,+∞)
7.已知, 判断、、之间的大小关系是( ).
A. B. C. D.
8.函数的反函数是( )
A. B.
C. D.
9.不等式的解集为 .
10.已知函数,对任意都有,则、 、的大小顺序是 .
11.(2018春 天津期末)若函数定义域为R,则a的取值范围是________.
12.若函数是奇函数,则为 .
13.已知,求函数的值域.
14.已知函数,其中x∈[0,3].
(1)求函数f(x)的最大值和最小值;
(2)若实数a满足:f(x)-a≥0恒成立,求a的取值范围.
15.(2018春 福建漳州月考)已知函数
(1)当a=4时,求函数f(x)的定义域;
(2)若对任意的x∈R,都有f(x)≥2成立,求实数a的取值范围.
【答案与解析】
1.【答案】A
【解析】.
2.【答案】D
【解析】不等式等价于或,解不等式组,可得或,即,故选D.
3.【答案】A
【解析】令,是的递减区间,即,是的递增区间,即递增且无最大值.
4.【答案】C
分析:要想判断函数的图象,我们可以先观察到函数的解析式中x的取值范围,得到其定义域从而得到图象的大致位置,再根据基本初等函数的性质,对其进行分析,找出符合函数性质的图象即可.
【解析】∵函数(a>0,a≠1)为增函数,
∴a>1,,
考察函数的定义域:由得x>-1,
则函数的定义域为:(-1,+∞),即函数图象只出现在直线x=-1轴右侧;
又函数可看成,的复合,
其中和均在各自的定义域是减函数,
从而得出函数在区间(-1,+∞)上递增,
且当x=0时,,即图象过原点,
分析A、B、C、D四个答案,只有C满足要求.
故选C.
点评:要想判断函数的图象,我们先要求出其定义域,再根据解析式,分析其单调性、奇偶性、周期性等性质,根据定义域、值域分析函数图象所处的区域,根据函数的性质分析函数图象的形状,如果还不能判断的话,可以代入特殊值,根据特殊点的位置进行判断.
5.【答案】D
【解析】.
故选D.
6.【答案】B
分析:本题必须保证:①使有意义,即a>0且a≠1,2-ax>0.②使在[0,1]上是x的减函数.由于所给函数可分解为,u=2-ax,其中u=2-ax在a>0时为减函数,所以必须a>1;③[0,1]必须是定义域的子集.
【解析】∵在[0,1]上是x的减函数,
∴f(0)>f(1),
即.
∴,
∴1<a<2.
故答案为:B.
点评:本题综合了多个知识点,需要概念清楚,推理正确.(1)复合函数的单调性;(2)函数定义域,对数真数大于零,底数大于0,不等于1.
7.【答案】B
【解析】先比较两个同底的,即与,因为函数是单调递减的,又,所以.再比较两个同指数的,即与,因为函数在上是增函数,又,所以.
8.【答案】D
【解析】由,解得即,故所求反函数为,故选D.
9.【答案】
【解析】依题意得,,,即,解得.
10.【答案】
【解析】因为,所以函数的对称轴为,又函数的开口向上,所以有离对称轴越远,函数值越大,所以
11.【答案】[-1,0]
【解析】∵函数定义域为R
∴恒成立即恒成立
则,解得-1≤a≤0
故答案为:[-1,0]
12.【答案】2
【解析】
.
13.【答案】
【解析】,令则,,即时,取得最大值12;当,即时,取得最小值-24,即的最大值为12,最小值为-24,所以函数的值域为.
14.【答案】(1),;(2)(-∞,-10]
分析:(1)由题意可得,(0≤x≤3),令,从而可转化为二次函数在区间[1,8]上的最值的求解
(2)由题意可得,a≥f(x)恒成立恒成立,结合(1)可求
【解析】(1)∵(0≤x≤3)
∴(0≤x≤3)
令,
∵0≤x≤3,
∴1≤t≤8.
令(1≤t≤8)
当t∈[1,2]时,h(t)是减函数;当t∈[2,8]时,h(t)是增函数.
∴,
(2)∵f(x)-a≥0恒成立,即a≤f(x)恒成立.
∴a≤f(x)min恒成立.
由(1)知,
∴a≤-10.
故a的取值范围为(-∞,-10]
点评:本题以指数函数的值域为载体,主要考查了二次函数在闭区间上的最值的求解,及函数的恒成立与函数最值的相互转化关系的应用.
15.【答案】(1)(―∞,―1)∪(1,+∞);(2)
【解析】(1)当a=4时,要使函数式有意义,则
|2x-1|+|x+2|>4,分类讨论如下:
①当时,2x-1+x+2>4,解得x>1;
②当时,1-2x+x+2>4,解得-2≤x<-1;
③当x<―2时,1―2x―x―2>4,解得x<-2,
综合以上讨论得,x∈(―∞,―1)∪(1,+∞);
(2)∵f(x)≥2恒成立,
∴|2x―1|+|x+2|―a>4恒成立,
分离参数a得,a<|2x―1|+|x+2|―4,
所以,a≤[|2x―1|+|x+2|―4]min,
记g(x)=|2x―1|+|x+2|―4,
分析可知,当时,,
所以,实数a的取值范围为.
【学习目标】
1.理解有理指数幂的含义,掌握幂的运算.
2.理解指数函数的概念和意义,理解指数函数的单调性与特殊点.
3.理解对数的概念及其运算性质.
4.重点理解指数函数、对数函数、幂函数的性质,熟练掌握指数、对数运算法则,明确算理,能对常见的指数型函数、对数型函数进行变形处理.
5.会求以指数函数、对数函数、幂函数为载体的复合函数的定义域、单调性及值域等性质.
6.知道指数函数与对数函数互为反函数(a>0,a≠1).
【知识框图】
/
【要点梳理】
要点一:指数及指数幂的运算
1.根式的概念
的次方根的定义:一般地,如果,那么叫做的次方根,其中
当为奇数时,正数的次方根为正数,负数的次方根是负数,表示为;当为偶数时,正数的次方根有两个,这两个数互为相反数可以表示为.
负数没有偶次方根,0的任何次方根都是0.
式子叫做根式,叫做根指数,叫做被开方数.
2.n次方根的性质:
(1)当为奇数时,;当为偶数时,
(2)
3.分数指数幂的意义:
;
要点诠释:
0的正分数指数幂等于0,负分数指数幂没有意义.
4.有理数指数幂的运算性质:
(1) (2) (3)
要点二:指数函数及其性质
1.指数函数概念
一般地,函数叫做指数函数,其中是自变量,函数的定义域为.
2.指数函数函数性质:
函数
名称
指数函数
定义
函数且叫做指数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的
变化情况
变化对图象的影响
在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小.
要点三:对数与对数运算
1.对数的定义
(1)若,则叫做以为底的对数,记作,其中叫做底数,叫做真数.
(2)负数和零没有对数.
(3)对数式与指数式的互化:.
2.几个重要的对数恒等式
,,.
3.常用对数与自然对数
常用对数:,即;自然对数:,即(其中…).
4.对数的运算性质
如果,那么
①加法:
②减法:
③数乘:
④
⑤
⑥换底公式:
要点四:对数函数及其性质
1.对数函数定义
一般地,函数叫做对数函数,其中是自变量,函数的定义域.
2.对数函数性质:
函数
名称
对数函数
定义
函数且叫做对数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的
变化情况
变化对图象的影响
在第一象限内,从顺时针方向看图象,逐渐增大;在第四象限内,从顺时针方向看图象,逐渐减小.
要点五:反函数
1.反函数的概念
设函数的定义域为,值域为,从式子中解出,得式子.如果对于在中的任何一个值,通过式子,在中都有唯一确定的值和它对应,那么式子表示是的函数,函数叫做函数的反函数,记作,习惯上改写成.
2.反函数的性质
(1)原函数与反函数的图象关于直线对称.
(2)函数的定义域、值域分别是其反函数的值域、定义域.
(3)若在原函数的图象上,则在反函数的图象上.
(4)一般地,函数要有反函数则它必须为单调函数.
要点六:幂函数
1.幂函数概念
形如/的函数,叫做幂函数,其中为常数.
2.幂函数的性质
(1)图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.
(2)过定点:所有的幂函数在都有定义,并且图象都通过点.
(3)单调性:如果,则幂函数的图象过原点,并且在上为增函数.如果,则幂函数的图象在上为减函数,在第一象限内,图象无限接近轴与轴.
(4)奇偶性:当为奇数时,幂函数为奇函数,当为偶数时,幂函数为偶函数.当(其中互质,和),若为奇数为奇数时,则是奇函数,若为奇数为偶数时,则是偶函数,若为偶数为奇数时,则是非奇非偶函数.
(5)图象特征:幂函数,当时,若,其图象在直线下方,若,其图象在直线上方,当时,若,其图象在直线上方,若,其图象在直线下方.
【典型例题】
类型一:指数、对数运算
例1.计算
(1) ; (2);
(3);(4)
【思路点拨】运算时尽量把根式转化为分数指数幂,而小数也要化为分数为好.
【答案】(1);(2)1;(3)3;(4)14.
【解析】(1)原式=;
(2)原式=
=
=1-+=1
(3)原式=
=
=2+=3;
(4)令,两边取常用对数得
=
=
=
即=14.
【总结升华】这是一组很基本的对数运算的练习题,虽然在考试中这些运算要求并不高,但是数式运算是学习数学的基本功,通过这样的运算练习熟练掌握运算公式、法则,以及学习数式变换的各种技巧.
举一反三:
【变式1】=( )
A.0 B.1 C.2 D.4
【答案】C
【解析】=.
【变式2】(1);(2).
【答案】(1)2;(2).
【解析】(1) 原式
;
(2) 原式
.
类型二:指数函数、对数函数、幂函数的图象与性质
例2.设偶函数满足,则= ( )
A. B.
C. D.
【答案】 B
【解析】且是偶函数.
或
或
解得或,故选B.
【总结升华】考查解不等式组及函数解析式,考查函数性质的综合运用.
举一反三:
【变式1】已知函数若,则的取值范围是( ).
A. B. 或 C. D. 或
【答案】A
【解析】依题意或即或,所以,故选A.
例3.设函数 若,则实数的取值范围是( ) .
A. B.
C. D.
【答案】C
【解析】解法一:①若,则,
,得,得,解得.
②若则,
,
解得
由①②可知
解法二:特殊值验证
令
,满足,故排除A、D.
令,,
不满足,故排除B.
【总结升华】本题考查了分段函数的性质、分类思想的应用.
例4.函数的单调递增区间是( )
A.(3,+∞) B.(-∞,3) C.(4,+∞) D.(-∞,2)
【思路点拨】这是一个内层函数是二次函数,外层函数是对数函数的复合函数,其单调性由这两个函数的单调性共同决定,即“同增异减”.
【答案】D
【解析】函数是由复合而成的,是减函数,在上单调递增,在上单调递减,由对数函数的真数必须大于零,即,解得或,所以原函数的单调递增区间是,故选D.
例5.(2018 上海模拟)已知函数(a>0,a≠1)在区间[―1,2]上的最大值为8,最小值为m.若函数是单调增函数,则a=________.
【思路点拨】根据题意求出m的取值范围,再讨论a的值,求出f(x)的单调性,从而求出a的值.
【答案】
【解析】根据题意,得3-10m>0,
解得;
当a>1时,函数在区间[-1,2]上单调递增,最大值为,解得,最小值为,不合题意,舍去;
当1>a>0时,函数在区间[―1,2]上单调递减,最大值为,解得,最小值为,满足题意;
综上,.
故答案为:.
【总结升华】本题主要考查指数函数的图象与性质的应用问题,通过讨论对数函数的底数确定函数的单调性是解决本题的关键.
举一反三:
【变式1】已知,该函数在区间[a,b]上的值域为[1,2],记满足该条件的实数a、b所形成的实数对为点P(a,b),则由点P构成的点集组成的图形为( )
A. 线段AD B. 线段AB
C. 线段AD与线段CD D. 线段AB与BC
【思路点拨】由指数函数的图象和性质,我们易构造出满足条件函数在闭区间[a,b]上的值域为[1,2]的不等式组,画出函数的图象后与答案进行比照,即可得到答案.
【答案】C
【解析】∵函数的图象为开口方向朝上,以x=1为对称轴的曲线,如图.
当x=1时,函数取最小值1,
若,则x=0,或x=1
而函数|在闭区间[a,b]上的值域为[1,2],
则或,
则有序实数对(a,b)在坐标平面内所对应点组成图形为
/
故选C.
【总结升华】本题考查的知识点是指数函数的性质,函数的值域,其中熟练掌指数函数在定区间上的值域问题,将已知转化为关于a,b的不等式组,是解答本题的关键.
【变式2】已知函数若互不相等,且,则的取值范围是( ).
A.(1,10) B.(5,6) C.(10,12) D.(20,24)
【答案】C
【解析】由互不相等,结合图象可知:这三个数分别在区间(0,1),(1,10),(10,12)上,不妨设,由得即,所以,所以,故选C.
【总结升华】考查利用图象求解的能力和对数的运算,考查数形结合的思想方法.
类型三:综合问题
例6.已知定义域为的函数是奇函数。
(Ⅰ)求的值;
(Ⅱ)若对任意的,不等式恒成立,求的取值范围
【思路点拨】(Ⅰ)利用奇函数的定义去解。(Ⅱ)先判断函数的单调性,由单调性脱掉函数符号,转化成二次函数问题去解决。
【答案】(Ⅰ),;(Ⅱ)
【解析】(Ⅰ)因为是奇函数,所以=0,即
又由f(1)=-f(-1)知
(Ⅱ)解法一:由(Ⅰ)知,易知在上
为减函数。又因是奇函数,从而不等式:
等价于=,因为减函数,由上式推得:
即对一切有:,
从而判别式
(或: 即对一切有:,又
∴
解法二:由(Ⅰ)知.又由题设条件得:
,
即 :,
整理得 ,因底数,故:
上式对一切均成立,从而判别式
【总结升华】对于含指数式、对数式等式的形式,解题思路是转化为不含指数、对数因式的普通等式或方程的形式,再来求解.
举一反三:
【变式1】已知函数,(a>0,且a≠1).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并说明理由;
(3)设,解不等式f(x)>0.
【解析】(1)依题意知,解得
函数f(x)的定义域为.
(2)函数是奇函数
任取,,所以
=0
所以函数是奇函数.
(3)因为,所以
由,得
解得
.
例7.设(其中a为实数),如果当时恒有成立,求实数a的取值范围.
【思路点拨】由题意知,原不等式转化成在上恒成立,只要求出不等式右边部分的最大值就可以了.
【答案】
【解析】依题意,在上恒成立.
则设
只需求的最大值
任取且
=
由于是单调递减函数
,即在上是单调递增的,
【总结升华】解决本题的关键是把转化成,转化成,这种问题以后还会碰到,希望同学们多注意.
举一反三:
【变式1】设函数.
(1)求的定义域;
(2)求使在上恒成立的实数的取值范围.
【解析】(1),即
若,则的定义域为;
若,则的定义域为;
若,则的定义域为.
(2)①当时,在的定义域内,等价于,即,于是问题等价于在上恒成立.
令,则在上递减,在上递增,,即.
另一方面要使在上恒成立,则必是定义域的子集,由(1)可知
由且可知.
②当时,在的定义域内,等价于,于是问题等价于在上恒成立.
显然这样的实数不存在.
综上所求的的取值范围为.
【巩固练习】
1.若函数在区间上的最大值是最小值的倍,则的值为( )
A. B. C. D.
2.设函数f(x)=/则满足的的取值范围是( )
A. B. C. D.
3.函数在上递减,那么在上( )
A.递增且无最大值 B.递减且无最小值
C.递增且有最大值 D.递减且有最小值
4.若函数(a>0,a≠1)为增函数,那么的图象是( )
/ / / /
A. B. C. D.
5.函数的定义域为( );
A. B.
C. D.
6.已知是[0,1]上的减函数,则a的取值范围为( )
A. (0,1) B. (1,2) C. (0,2) D. [2,+∞)
7.已知, 判断、、之间的大小关系是( ).
A. B. C. D.
8.函数的反函数是( )
A. B.
C. D.
9.不等式的解集为 .
10.已知函数,对任意都有,则、 、的大小顺序是 .
11.(2018春 天津期末)若函数定义域为R,则a的取值范围是________.
12.若函数是奇函数,则为 .
13.已知,求函数的值域.
14.已知函数,其中x∈[0,3].
(1)求函数f(x)的最大值和最小值;
(2)若实数a满足:f(x)-a≥0恒成立,求a的取值范围.
15.(2018春 福建漳州月考)已知函数
(1)当a=4时,求函数f(x)的定义域;
(2)若对任意的x∈R,都有f(x)≥2成立,求实数a的取值范围.
【答案与解析】
1.【答案】A
【解析】.
2.【答案】D
【解析】不等式等价于或,解不等式组,可得或,即,故选D.
3.【答案】A
【解析】令,是的递减区间,即,是的递增区间,即递增且无最大值.
4.【答案】C
分析:要想判断函数的图象,我们可以先观察到函数的解析式中x的取值范围,得到其定义域从而得到图象的大致位置,再根据基本初等函数的性质,对其进行分析,找出符合函数性质的图象即可.
【解析】∵函数(a>0,a≠1)为增函数,
∴a>1,,
考察函数的定义域:由得x>-1,
则函数的定义域为:(-1,+∞),即函数图象只出现在直线x=-1轴右侧;
又函数可看成,的复合,
其中和均在各自的定义域是减函数,
从而得出函数在区间(-1,+∞)上递增,
且当x=0时,,即图象过原点,
分析A、B、C、D四个答案,只有C满足要求.
故选C.
点评:要想判断函数的图象,我们先要求出其定义域,再根据解析式,分析其单调性、奇偶性、周期性等性质,根据定义域、值域分析函数图象所处的区域,根据函数的性质分析函数图象的形状,如果还不能判断的话,可以代入特殊值,根据特殊点的位置进行判断.
5.【答案】D
【解析】.
故选D.
6.【答案】B
分析:本题必须保证:①使有意义,即a>0且a≠1,2-ax>0.②使在[0,1]上是x的减函数.由于所给函数可分解为,u=2-ax,其中u=2-ax在a>0时为减函数,所以必须a>1;③[0,1]必须是定义域的子集.
【解析】∵在[0,1]上是x的减函数,
∴f(0)>f(1),
即.
∴,
∴1<a<2.
故答案为:B.
点评:本题综合了多个知识点,需要概念清楚,推理正确.(1)复合函数的单调性;(2)函数定义域,对数真数大于零,底数大于0,不等于1.
7.【答案】B
【解析】先比较两个同底的,即与,因为函数是单调递减的,又,所以.再比较两个同指数的,即与,因为函数在上是增函数,又,所以.
8.【答案】D
【解析】由,解得即,故所求反函数为,故选D.
9.【答案】
【解析】依题意得,,,即,解得.
10.【答案】
【解析】因为,所以函数的对称轴为,又函数的开口向上,所以有离对称轴越远,函数值越大,所以
11.【答案】[-1,0]
【解析】∵函数定义域为R
∴恒成立即恒成立
则,解得-1≤a≤0
故答案为:[-1,0]
12.【答案】2
【解析】
.
13.【答案】
【解析】,令则,,即时,取得最大值12;当,即时,取得最小值-24,即的最大值为12,最小值为-24,所以函数的值域为.
14.【答案】(1),;(2)(-∞,-10]
分析:(1)由题意可得,(0≤x≤3),令,从而可转化为二次函数在区间[1,8]上的最值的求解
(2)由题意可得,a≥f(x)恒成立恒成立,结合(1)可求
【解析】(1)∵(0≤x≤3)
∴(0≤x≤3)
令,
∵0≤x≤3,
∴1≤t≤8.
令(1≤t≤8)
当t∈[1,2]时,h(t)是减函数;当t∈[2,8]时,h(t)是增函数.
∴,
(2)∵f(x)-a≥0恒成立,即a≤f(x)恒成立.
∴a≤f(x)min恒成立.
由(1)知,
∴a≤-10.
故a的取值范围为(-∞,-10]
点评:本题以指数函数的值域为载体,主要考查了二次函数在闭区间上的最值的求解,及函数的恒成立与函数最值的相互转化关系的应用.
15.【答案】(1)(―∞,―1)∪(1,+∞);(2)
【解析】(1)当a=4时,要使函数式有意义,则
|2x-1|+|x+2|>4,分类讨论如下:
①当时,2x-1+x+2>4,解得x>1;
②当时,1-2x+x+2>4,解得-2≤x<-1;
③当x<―2时,1―2x―x―2>4,解得x<-2,
综合以上讨论得,x∈(―∞,―1)∪(1,+∞);
(2)∵f(x)≥2恒成立,
∴|2x―1|+|x+2|―a>4恒成立,
分离参数a得,a<|2x―1|+|x+2|―4,
所以,a≤[|2x―1|+|x+2|―4]min,
记g(x)=|2x―1|+|x+2|―4,
分析可知,当时,,
所以,实数a的取值范围为.
