高中数学必修一知识讲解,巩固练习(复习补习,期末复习资料):30【基础】函数模型的应用实例
文档属性
| 名称 | 高中数学必修一知识讲解,巩固练习(复习补习,期末复习资料):30【基础】函数模型的应用实例 |
|
|
| 格式 | zip | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 11:14:29 | ||
图片预览





文档简介
函数模型的应用实例
【学习目标】
1.能够找出简单实际问题中的函数关系式,应用指数函数、对数函数模型解决实际问题,并初步掌握数学建模的一般步骤和方法.
2.通过具体实例,感受运用函数建立模型的过程和方法,体会指数函数、对数函数模型在数学和其他学科中的应用.
3.通过函数应用的学习,体会数学应用的广泛性,树立事物间相互联系的辩证观,培养分析问题、解决问题的能力,增强数学的应用意识.
【要点梳理】
要点一:解答应用问题的基本思想和步骤
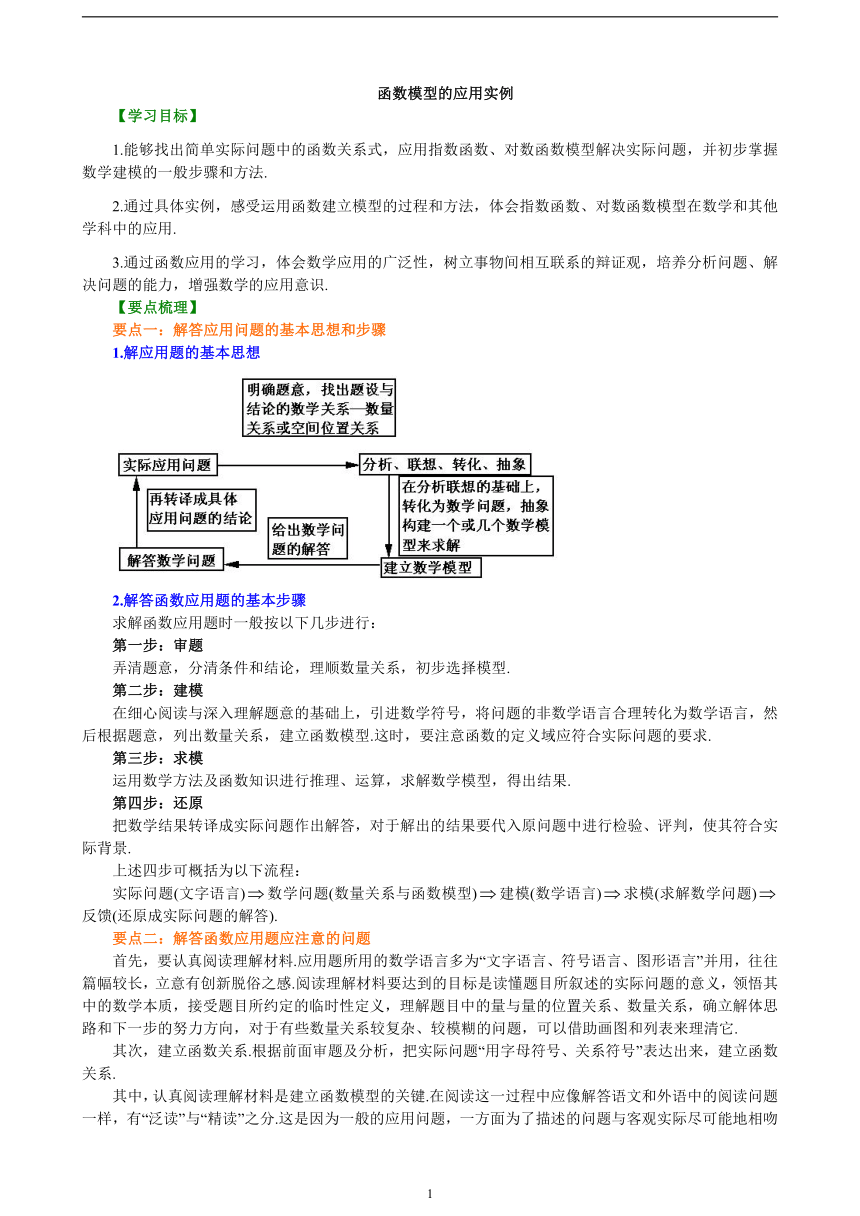
1.解应用题的基本思想
/
2.解答函数应用题的基本步骤
求解函数应用题时一般按以下几步进行:
第一步:审题
弄清题意,分清条件和结论,理顺数量关系,初步选择模型.
第二步:建模
在细心阅读与深入理解题意的基础上,引进数学符号,将问题的非数学语言合理转化为数学语言,然后根据题意,列出数量关系,建立函数模型.这时,要注意函数的定义域应符合实际问题的要求.
第三步:求模
运用数学方法及函数知识进行推理、运算,求解数学模型,得出结果.
第四步:还原
把数学结果转译成实际问题作出解答,对于解出的结果要代入原问题中进行检验、评判,使其符合实际背景.
上述四步可概括为以下流程:
实际问题(文字语言)数学问题(数量关系与函数模型)建模(数学语言)求模(求解数学问题)反馈(还原成实际问题的解答).
要点二:解答函数应用题应注意的问题
首先,要认真阅读理解材料.应用题所用的数学语言多为“文字语言、符号语言、图形语言”并用,往往篇幅较长,立意有创新脱俗之感.阅读理解材料要达到的目标是读懂题目所叙述的实际问题的意义,领悟其中的数学本质,接受题目所约定的临时性定义,理解题目中的量与量的位置关系、数量关系,确立解体思路和下一步的努力方向,对于有些数量关系较复杂、较模糊的问题,可以借助画图和列表来理清它.
其次,建立函数关系.根据前面审题及分析,把实际问题“用字母符号、关系符号”表达出来,建立函数关系.
其中,认真阅读理解材料是建立函数模型的关键.在阅读这一过程中应像解答语文和外语中的阅读问题一样,有“泛读”与“精读”之分.这是因为一般的应用问题,一方面为了描述的问题与客观实际尽可能地相吻合,就必须用一定的篇幅描述其中的情境;另一方面有时为了思想教育方面的需要,也要用一些非数量关系的语言来叙述,而我们解决问题所关心的东西是数量关系,因此对那些叙述的部分只需要“泛读”即可.反过来,对那些刻画数量关系、位置关系、对应关系等与数学有关的问题的部分,则应“精读”,一遍不行再来一遍,直到透彻地理解为止,此时切忌草率.
【典型例题】
类型一、已建立函数模型的应用题
例1.心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间.讲座开始时,学生的兴趣激增,中间有一段不太长时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用f (x)表示学生掌握和接受概念的能力,x表示提出和讲授概念的时间(单位:分),可有以下的公式:
.
问开讲后多少分钟,学生的接受能力最强?能维持多长时间?
【答案】开讲后10分钟,学生达到最强的接受能力(值为59),并维持6分钟.
【解析】 当0<x≤10时,
f (x)=―0.1x2+2.6x+43=―0.1(x―13)2+59.9,
可知f (x)在(0,10)上单调递增,故其最大值为
f (10)=―0.1×(―3)2+59.9=59.
显然,当16<x≤30时,f (x)递减,
f (x)<-3×16+107=59.
因此,开讲后10分钟,学生达到最强的接受能力(值为59),并维持6分钟.
【总结升华】(1)解决分段函数模型问题的关键在于“分段归类”,即自变量属于哪一段就选用哪段的函数【解析】式来分析解决问题.(2)求解“已建立数学模型”的应用问题关键是抓住已建立的函数模型,选择合适的方法求解建立的数学模型.注意一定要“读”懂模型.
例2.某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入R(x)(万元)满足,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入-总成本);
(2)工厂生产多少台产品时,可使盈利最多?
【思路点拨】(1)由题意得G(x)=2.8+x.由,f(x)=R(x)-G(x),能写出利润函数y=f(x)的解析式.
(2)当x>5时,由函数f(x)递减,知f(x)<f(5)=3.2(万元).当0≤x≤5时,函数,当x=4时,f(x)有最大值为3.6(万元).由此能求出工厂生产多少台产品时,可使盈利最多.
【答案】(1);(2)400
【解析】(1)由题意得G(x)=2.8+x.
∵,
∴.
(2)当x>5时,
∵函数f(x)递减,
∴f(x)<f(5)=3.2(万元).
当0≤x≤5时,函数,
当x=4时,f(x)有最大值为3.6(万元).
所以当工厂生产4百台时,可使赢利最大为3.6万元.
【总结升华】本题考查函数知识在生产实际中的具体应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
举一反三:
【变式1】 设在海拔x m处的大气压强是y Pa,y与x之间的函数关系式是y=cekx,其中c,k为常量,已知某地某天海平面上的大气压为1.01×105 Pa,1000 m高空的大气压为0.90×105 Pa,求600 m高空的大气压强(结果保留3位有效数字).
【答案】 0.943×105.
【解析】这里已有函数模型,要求待定系数c、k,由x=0时y=1.01×105 Pa和x=1000 m时y=0.90×105 Pa可求.
将x=0,y=1.01×105,x=1000,y=0.90×105分别代入函数关系式y=cekx中,得
,∴.
将c=1.01×105代入0.90×105=ce1000k中得0.90×105=1.01×105e1000k,
∴.
由计算器算得k=-1.15×10-4,
∴.
将x=600代入上述函数关系式得,
由计算器算得y=0.943×105 Pa.
答:600 m高空的大气压强约为0.943×105 Pa.
【总结升华】 函数y=c·akx(a、c、k为常数)是一个应用广泛的函数模型,它在电学、生物学、人口学、气象学等都有广泛的应用,解决这类给出指数函数模型的应用题的基本方法是待定系数法,即根据题意确定相关的系数即可.
类型二、自建函数模型的应用问题
例3. (2018 湖南岳阳月考)旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为16000元.旅行团中的每个人的飞机标按以下方式与旅行社结算:若旅行团的人数不超过35人时,飞机票每张收费800元;若旅行团的人数多于35人时,则予以优惠,每多1人,每个人的机票费减少10元,但旅行团的人数最多不超过60人.设旅行团的人数为x人,飞机票价格为y元,旅行社的利润为Q元.
(1)写出飞机票价格y元与旅行团人数x之间的函数关系式;
(2)当旅行团人数x为多少时,旅行社可获得最大利润?求出最大利润.
【思路点拨】(1)依题意得,当1≤x≤35时,y=800;当35<x≤60时,y=800―10(x―35)=―10x+1150,从而得出结论.
(2)设利润为Q,则由Q=yx―1600可得Q的解析式.当1≤x≤35且x∈N时,求得的值,当35<x≤60且x∈N时,再根据Q的解析式求得的值,再把这两个的值作比较,可得结论.
【答案】(1);(2)当x=57或x=58时,=17060>12000
【解析】(1)依题意得,当1≤x≤35时,y=800.
当35<x≤60时,y=800―10(x―35)=―10x+1150;
∴.
(2)设利润为Q,则
.
当1≤x≤35且x∈N时,=800×5-16000=12000,
当35<x≤60且x∈N时,,
因为x∈N,所以当x=57或x=58时,=17060>12000.
故当旅游团人数为57或58时,旅行社可获得最大利润为17060元.
【总结升华】本题主要考查求函数最值的应用,二次函数的性质,体现了分类讨论的数学思想.
举一反三:
【变式1】某商场销售某一品牌的羊毛衫,假设每天购买人数与每件羊毛衫的标价(元)之间满足关系式m=kx+b(k、b为实常数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元,且当x=200时,m=100.已知这种羊毛衫的成本价是每件100元,商场以高于成本价的相同价格(标价)x元出售.
(Ⅰ)求实常数k、b的值;
(Ⅱ)若为使商场每天获得的利润最大,那么每件羊毛衫的标价应为多少元?
【答案】(Ⅰ);(Ⅱ)当x=200时,最大值为10000元
【解析】(Ⅰ)由题意得:;
(Ⅱ)设商场每天获取的利润为,∵,则
,
,
∴当时,取最大值为10000元;
即为使商场每天要获取的利润最大,每件羊毛衫的标价为200元.
例4.某环线地铁按内、外环线同时运行,内、外环线的长均为30千米(忽略内、外环线长度差异).
(1)当9列列车同时在内环线上运行时,要使内环线乘客最长候车时间为10分钟,求内环线列车的最小平均速度;
(2)新调整的方案要求内环线列车平均速度为25千米/小时,外环线列车平均速度为30千米/小时.现内、外环线共有18列列车全部投入运行,要使内、外环线乘客的最长候车时间之差不超过1分钟,问:内、外环线应各投入几列列车运行?
【思路点拨】(1)根据题意列出不等式求解(2)列出不等式求解,因为计算过程中,数字比较大,可以使用计算器。
【答案】(1)20(2)10 8
【解析】
(1)设内环线列车平均速度最小为
由题得:
解得。
答:内环线列车的最小平均速度为每小时20千米。
(2)设内、外环线分别投入列车数量为、列
由题得:
即
得,
解得:,由计算器得:。
答:内、外环线应各投入10列、8列列车运行,才能使内、外环线乘客的最长候车时间之差不超过1分钟
类型三、拟和函数模型的应用问题
这类应用题提供的变量关系是不确定的,只是给出了两个变量的几组对应值(是搜集或用实验方法测定的).为了降低难度,有时采用限定函数模型范围的方法.
例5. 某汽车公司曾在2009年初公告:2009年销量目标定为39.3万辆;且该公司重事长极力表示有信心完成这个销量目标.
2006年,某汽车年销量8万辆;
2007年,某汽车年销量18万辆;
2008年,某汽车年销量30万辆.
如果我们分别将2006,2007,2008,2009年定义为第一,二,三,四年,现在有两个函数模型:二次函数型f (x)=ax2+bx+c(a≠0),指数函数型g (x)=a·bx+c(a≠0,b≠1,b>0),哪个模型能更好地反映该公司年销量y与第x年的关系?
【解析】建立年销量y(万辆)与第x年的函数,可知函数图象必过点(1,8),(2,18),(3,30).
(1)构造二次函数型f (x)=ax2+bx+c(a≠0),
将点的坐标代入,可得,解得.
则f (x)=x2+7x,故f (4)=44,与计划误差为4.7.
(2)构造指函数型g (x)=a·bx+c,将点的坐标代入,
可得,解得,则,
故,与计划误差为5.1.
由上可得f (x)=x2+7x模型能更好地反映该公司年销量y(万辆)与第x年的关系.
【总结升华】某个函数模型能否更好地反映变量间的关系,必须与实际数据的误差相对较小.
举一反三:
【变式1】某地区不同身高的未成年男性的体重平均值如下表:
身高/cm
60
70
80
90
100
110
120
130
140
150
160
170
体重/kg
6.13
7.90
9.99
12.15
15.02
17.50
20.92
26.86
31.11
38.85
47.25
55.05
若体重超过相同身高男性平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高175cm,体重为78kg的在校男生的体重是否正常?
【解析】 本例没有给出函数模型,所以我们要先画出草图,再根据图象与我们学习过的函数图象进行比较,猜测出函数模型.
以身高为横坐标,体重为纵坐标,画出由离散点构成的草图,如图所示.
根据点的分布情况,结合以前学过的指数函数图象特征,可猜测以(a>0,a≠1 )为男性的体重与身高关系的函数模型.
把点(70,7.90)、(160,47.25)代入函数以中,得
使用计算器可求得
所以,函数模型为.
用计算器验证其它点与模拟函数的关系,发现拟和程度相符.
再将x=175代入函数式,即,用计算器求得y≈63.98.
因为≈1.22>1.2,所以,这个男生偏胖.
【总结升华】由于本题没有给出函数模型,因此需要根据题目中的有关数据描绘出基本草图,然后根据直观性,去和已学过的有关函数图象对照、比较,由此猜测函数模型.在解此类问题的过程中,首先需要在实际的情境中去理解、分析所给的一系列数据,舍弃与解题无关的因素,抽象转化为数学模型.
【巩固练习】
1.某学校开展研究性学习活动,一组同学获得了下面的一组实验数据:
1.99
3
4
5.1
6.12
1.5
4.04
7.5
12
18.01
现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
A. B. C. D.
2.一辆汽车在某段路程中的行驶路程s关于时间t变化的图象如下图所示,那么图象所应对的函数模型是( )
A.分段函数 B.二次函数 C.指数函数 D.对数函数
3.某厂日产手套总成本y(元)与手套日产量x(副)的函数解析式为y=5x+4000,而手套出厂价格为每副10元,则该厂为了不亏本,日产手套至少为( )
A.200副 B.400副 C.600副 D.800副
4.(2018 四川广元模拟)某城区按以下规定收取水费:若每月和水不超过20 m3,则每立方米水费按2元收取;若超过20 m3,则超过的部分按每立方米3元收取,如果某户居民在某月所交水费的平均价为每立方米2.20元,则这户居民这月共用水( )
A.46 m3 B.44 m3 C.26 m3 D.25 m3
5.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系(a,b,c是常数),右图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
/
6.一高为H、满缸水量为V的鱼缸截面如右图所示,其底部破了一个小洞,缸中水从洞中流出.若鱼缸水深为h时的水的体积为v,则函数v=f (h)的大致图象可能是下图中四个选项中的( )
/
7.下表列出了一项试验的统计数据,表示将皮球从高h米处落下,弹跳高度d与下落高度h的关系:
h(米)
50
80
100
150
…
d(米)
25
40
50
75
…
写出一个能表示这种关系的式子为________.
8.某工厂生产某种产品的固定成本为2000万元,并且每生产一单位产品,成本增加10万元,又知总收入k(万元)是单位产品数Q的函数,,则总利润L(Q)的最大值是________.
9.某种细菌经30分钟繁殖为原来的2倍,且知该细菌的繁殖规律为y=ekt,其中k为常数,t表示时间(单位:小时),y表示细菌个数,则k=________,经过5小时,1个细菌能繁殖为________个.
10.已知某地今年年初拥有居民住房的总面积为a(单位:m2),其中有部分旧住房需要拆除.当地有关部门决定每年以当年年初住房面积的10%建设新住房,同事也拆除面积为b(单位:m2)的旧住房.
(Ⅰ)分别写出第一年末和第二年末的实际住房面积的表达式:
(Ⅱ)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)
11.(2018 山东模拟)已知某城市2017年底的人口总数为200元,假设此后该城市人口的年增长率 1%(不考虑其他因素).
(1)若经过x年该城市人口总数为y万,试写出y关于x的函数关系式;
(2)如果该城市人口总数达到210万,那么至少需要经过多少年(精确到1年)?
12.某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价x元与日销售量y件之间有如下关系:
x 45 50
y 27 12
(Ⅰ)确定x与y的一个一次函数关系式y=f(x);
(Ⅱ)若日销售利润为P元,根据(I)中关系写出P关于x的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
【答案与解析】
1.【答案】D
【解析】把的值分别代入四个函数式,结果最最近的就是。
2.【答案】A
【解析】 由图象知,在不同时段内,路程折线图不同,故对应的函数模型为分段函数.
3.分析:根据题意列出出/厂价格和成本之间的不等关系式:5x+4000≤10x,解出即可.
【答案】D
【解析】由5x+4000≤10x,解得x≥800,即日产手套至少800副时才不亏本.
故选D.
点评:主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解.
4.【答案】D
【解析】设他这个月共用了x立方米的水
20×2+(x-20)×3=2.2x
40+3x-60=2.2x
0.8x=20
x=25.
他这个月共用了25立方米的水.
故选:D.
5.【答案】3.75
【解析】由题意得解之得
∴,最佳加工时间应是p最高的时候,
当t=3.75时,p有最大值.故填3.75.
6.【答案】B
【解析】由鱼缸的形状可知,水的体积随h的减小,一开始减少得慢,后来又减少得快,然后再减少得慢.
7.【答案】
【解析】观察表中数据即可.
8.【答案】2500万元
【解析】 总利润L=总收入k-总支出(生产成本+固定成本).所以.故当Q=300时,总利润的最大值为2500万元.
9.【答案】2ln2 1024
【解析】 将代入,得,所以,k=2ln2,这时函数关系式为,令t=5(小时),得y=210=1024(个).
10.【解析】(Ⅰ)第1年末的住房面积.
第2年末的住房面积(a·-b)·-b=a·()2-b(1+)=1.21a-2.1b(m2).
(Ⅱ)第3年末的住房面积[a·()3-b(1+)]-b=a·()3-b[1++()2].
第4年末住房面积为a·()4-b[1++()2+()3].
第5年末住房面积为a·()5-b[1++()2+()3+()4]=1.15a-b=1.6a-6b
依题意可知,1.6a-6b=1.3a,解得b=,所以每年拆除的旧房面积为(m2).
11.【答案】(1);(2)5年
【解析】(1).
(2)令y=210,即,解得.
答:要经过5年该城市人口总数达到210万.
12.分析:(Ⅰ)设出y=f(x)的表达式,利用已知条件列出方程组求解即可得到函数的解析式;
(Ⅱ)若日销售利润为P元,根据(I)中关系直接写出P关于x的函数关系,然后利用二次函数闭区间的最值即可求解最大的日销售利润.
【答案】(Ⅰ)y=162-3x,且0≤x≤54;(Ⅱ)42元
【解析】(Ⅰ)因为f(x)为一次函数,设y=ax+b,解方程组
得a=-3,b=162,
故y=162-3x为所求的函数关系式,
又∵y≥0,∴0≤x≤54.
(Ⅱ)依题意得:
.
当x=42时,,
即销售单价为42元/件时,获得最大日销售利润.
点评:本题考查函数的模型的选择与应用,二次函数闭区间上的最值的求法,考查分析问题解决问题的能力.
【学习目标】
1.能够找出简单实际问题中的函数关系式,应用指数函数、对数函数模型解决实际问题,并初步掌握数学建模的一般步骤和方法.
2.通过具体实例,感受运用函数建立模型的过程和方法,体会指数函数、对数函数模型在数学和其他学科中的应用.
3.通过函数应用的学习,体会数学应用的广泛性,树立事物间相互联系的辩证观,培养分析问题、解决问题的能力,增强数学的应用意识.
【要点梳理】
要点一:解答应用问题的基本思想和步骤
1.解应用题的基本思想
/
2.解答函数应用题的基本步骤
求解函数应用题时一般按以下几步进行:
第一步:审题
弄清题意,分清条件和结论,理顺数量关系,初步选择模型.
第二步:建模
在细心阅读与深入理解题意的基础上,引进数学符号,将问题的非数学语言合理转化为数学语言,然后根据题意,列出数量关系,建立函数模型.这时,要注意函数的定义域应符合实际问题的要求.
第三步:求模
运用数学方法及函数知识进行推理、运算,求解数学模型,得出结果.
第四步:还原
把数学结果转译成实际问题作出解答,对于解出的结果要代入原问题中进行检验、评判,使其符合实际背景.
上述四步可概括为以下流程:
实际问题(文字语言)数学问题(数量关系与函数模型)建模(数学语言)求模(求解数学问题)反馈(还原成实际问题的解答).
要点二:解答函数应用题应注意的问题
首先,要认真阅读理解材料.应用题所用的数学语言多为“文字语言、符号语言、图形语言”并用,往往篇幅较长,立意有创新脱俗之感.阅读理解材料要达到的目标是读懂题目所叙述的实际问题的意义,领悟其中的数学本质,接受题目所约定的临时性定义,理解题目中的量与量的位置关系、数量关系,确立解体思路和下一步的努力方向,对于有些数量关系较复杂、较模糊的问题,可以借助画图和列表来理清它.
其次,建立函数关系.根据前面审题及分析,把实际问题“用字母符号、关系符号”表达出来,建立函数关系.
其中,认真阅读理解材料是建立函数模型的关键.在阅读这一过程中应像解答语文和外语中的阅读问题一样,有“泛读”与“精读”之分.这是因为一般的应用问题,一方面为了描述的问题与客观实际尽可能地相吻合,就必须用一定的篇幅描述其中的情境;另一方面有时为了思想教育方面的需要,也要用一些非数量关系的语言来叙述,而我们解决问题所关心的东西是数量关系,因此对那些叙述的部分只需要“泛读”即可.反过来,对那些刻画数量关系、位置关系、对应关系等与数学有关的问题的部分,则应“精读”,一遍不行再来一遍,直到透彻地理解为止,此时切忌草率.
【典型例题】
类型一、已建立函数模型的应用题
例1.心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间.讲座开始时,学生的兴趣激增,中间有一段不太长时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用f (x)表示学生掌握和接受概念的能力,x表示提出和讲授概念的时间(单位:分),可有以下的公式:
.
问开讲后多少分钟,学生的接受能力最强?能维持多长时间?
【答案】开讲后10分钟,学生达到最强的接受能力(值为59),并维持6分钟.
【解析】 当0<x≤10时,
f (x)=―0.1x2+2.6x+43=―0.1(x―13)2+59.9,
可知f (x)在(0,10)上单调递增,故其最大值为
f (10)=―0.1×(―3)2+59.9=59.
显然,当16<x≤30时,f (x)递减,
f (x)<-3×16+107=59.
因此,开讲后10分钟,学生达到最强的接受能力(值为59),并维持6分钟.
【总结升华】(1)解决分段函数模型问题的关键在于“分段归类”,即自变量属于哪一段就选用哪段的函数【解析】式来分析解决问题.(2)求解“已建立数学模型”的应用问题关键是抓住已建立的函数模型,选择合适的方法求解建立的数学模型.注意一定要“读”懂模型.
例2.某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入R(x)(万元)满足,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入-总成本);
(2)工厂生产多少台产品时,可使盈利最多?
【思路点拨】(1)由题意得G(x)=2.8+x.由,f(x)=R(x)-G(x),能写出利润函数y=f(x)的解析式.
(2)当x>5时,由函数f(x)递减,知f(x)<f(5)=3.2(万元).当0≤x≤5时,函数,当x=4时,f(x)有最大值为3.6(万元).由此能求出工厂生产多少台产品时,可使盈利最多.
【答案】(1);(2)400
【解析】(1)由题意得G(x)=2.8+x.
∵,
∴.
(2)当x>5时,
∵函数f(x)递减,
∴f(x)<f(5)=3.2(万元).
当0≤x≤5时,函数,
当x=4时,f(x)有最大值为3.6(万元).
所以当工厂生产4百台时,可使赢利最大为3.6万元.
【总结升华】本题考查函数知识在生产实际中的具体应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
举一反三:
【变式1】 设在海拔x m处的大气压强是y Pa,y与x之间的函数关系式是y=cekx,其中c,k为常量,已知某地某天海平面上的大气压为1.01×105 Pa,1000 m高空的大气压为0.90×105 Pa,求600 m高空的大气压强(结果保留3位有效数字).
【答案】 0.943×105.
【解析】这里已有函数模型,要求待定系数c、k,由x=0时y=1.01×105 Pa和x=1000 m时y=0.90×105 Pa可求.
将x=0,y=1.01×105,x=1000,y=0.90×105分别代入函数关系式y=cekx中,得
,∴.
将c=1.01×105代入0.90×105=ce1000k中得0.90×105=1.01×105e1000k,
∴.
由计算器算得k=-1.15×10-4,
∴.
将x=600代入上述函数关系式得,
由计算器算得y=0.943×105 Pa.
答:600 m高空的大气压强约为0.943×105 Pa.
【总结升华】 函数y=c·akx(a、c、k为常数)是一个应用广泛的函数模型,它在电学、生物学、人口学、气象学等都有广泛的应用,解决这类给出指数函数模型的应用题的基本方法是待定系数法,即根据题意确定相关的系数即可.
类型二、自建函数模型的应用问题
例3. (2018 湖南岳阳月考)旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为16000元.旅行团中的每个人的飞机标按以下方式与旅行社结算:若旅行团的人数不超过35人时,飞机票每张收费800元;若旅行团的人数多于35人时,则予以优惠,每多1人,每个人的机票费减少10元,但旅行团的人数最多不超过60人.设旅行团的人数为x人,飞机票价格为y元,旅行社的利润为Q元.
(1)写出飞机票价格y元与旅行团人数x之间的函数关系式;
(2)当旅行团人数x为多少时,旅行社可获得最大利润?求出最大利润.
【思路点拨】(1)依题意得,当1≤x≤35时,y=800;当35<x≤60时,y=800―10(x―35)=―10x+1150,从而得出结论.
(2)设利润为Q,则由Q=yx―1600可得Q的解析式.当1≤x≤35且x∈N时,求得的值,当35<x≤60且x∈N时,再根据Q的解析式求得的值,再把这两个的值作比较,可得结论.
【答案】(1);(2)当x=57或x=58时,=17060>12000
【解析】(1)依题意得,当1≤x≤35时,y=800.
当35<x≤60时,y=800―10(x―35)=―10x+1150;
∴.
(2)设利润为Q,则
.
当1≤x≤35且x∈N时,=800×5-16000=12000,
当35<x≤60且x∈N时,,
因为x∈N,所以当x=57或x=58时,=17060>12000.
故当旅游团人数为57或58时,旅行社可获得最大利润为17060元.
【总结升华】本题主要考查求函数最值的应用,二次函数的性质,体现了分类讨论的数学思想.
举一反三:
【变式1】某商场销售某一品牌的羊毛衫,假设每天购买人数与每件羊毛衫的标价(元)之间满足关系式m=kx+b(k、b为实常数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元,且当x=200时,m=100.已知这种羊毛衫的成本价是每件100元,商场以高于成本价的相同价格(标价)x元出售.
(Ⅰ)求实常数k、b的值;
(Ⅱ)若为使商场每天获得的利润最大,那么每件羊毛衫的标价应为多少元?
【答案】(Ⅰ);(Ⅱ)当x=200时,最大值为10000元
【解析】(Ⅰ)由题意得:;
(Ⅱ)设商场每天获取的利润为,∵,则
,
,
∴当时,取最大值为10000元;
即为使商场每天要获取的利润最大,每件羊毛衫的标价为200元.
例4.某环线地铁按内、外环线同时运行,内、外环线的长均为30千米(忽略内、外环线长度差异).
(1)当9列列车同时在内环线上运行时,要使内环线乘客最长候车时间为10分钟,求内环线列车的最小平均速度;
(2)新调整的方案要求内环线列车平均速度为25千米/小时,外环线列车平均速度为30千米/小时.现内、外环线共有18列列车全部投入运行,要使内、外环线乘客的最长候车时间之差不超过1分钟,问:内、外环线应各投入几列列车运行?
【思路点拨】(1)根据题意列出不等式求解(2)列出不等式求解,因为计算过程中,数字比较大,可以使用计算器。
【答案】(1)20(2)10 8
【解析】
(1)设内环线列车平均速度最小为
由题得:
解得。
答:内环线列车的最小平均速度为每小时20千米。
(2)设内、外环线分别投入列车数量为、列
由题得:
即
得,
解得:,由计算器得:。
答:内、外环线应各投入10列、8列列车运行,才能使内、外环线乘客的最长候车时间之差不超过1分钟
类型三、拟和函数模型的应用问题
这类应用题提供的变量关系是不确定的,只是给出了两个变量的几组对应值(是搜集或用实验方法测定的).为了降低难度,有时采用限定函数模型范围的方法.
例5. 某汽车公司曾在2009年初公告:2009年销量目标定为39.3万辆;且该公司重事长极力表示有信心完成这个销量目标.
2006年,某汽车年销量8万辆;
2007年,某汽车年销量18万辆;
2008年,某汽车年销量30万辆.
如果我们分别将2006,2007,2008,2009年定义为第一,二,三,四年,现在有两个函数模型:二次函数型f (x)=ax2+bx+c(a≠0),指数函数型g (x)=a·bx+c(a≠0,b≠1,b>0),哪个模型能更好地反映该公司年销量y与第x年的关系?
【解析】建立年销量y(万辆)与第x年的函数,可知函数图象必过点(1,8),(2,18),(3,30).
(1)构造二次函数型f (x)=ax2+bx+c(a≠0),
将点的坐标代入,可得,解得.
则f (x)=x2+7x,故f (4)=44,与计划误差为4.7.
(2)构造指函数型g (x)=a·bx+c,将点的坐标代入,
可得,解得,则,
故,与计划误差为5.1.
由上可得f (x)=x2+7x模型能更好地反映该公司年销量y(万辆)与第x年的关系.
【总结升华】某个函数模型能否更好地反映变量间的关系,必须与实际数据的误差相对较小.
举一反三:
【变式1】某地区不同身高的未成年男性的体重平均值如下表:
身高/cm
60
70
80
90
100
110
120
130
140
150
160
170
体重/kg
6.13
7.90
9.99
12.15
15.02
17.50
20.92
26.86
31.11
38.85
47.25
55.05
若体重超过相同身高男性平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高175cm,体重为78kg的在校男生的体重是否正常?
【解析】 本例没有给出函数模型,所以我们要先画出草图,再根据图象与我们学习过的函数图象进行比较,猜测出函数模型.
以身高为横坐标,体重为纵坐标,画出由离散点构成的草图,如图所示.
根据点的分布情况,结合以前学过的指数函数图象特征,可猜测以(a>0,a≠1 )为男性的体重与身高关系的函数模型.
把点(70,7.90)、(160,47.25)代入函数以中,得
使用计算器可求得
所以,函数模型为.
用计算器验证其它点与模拟函数的关系,发现拟和程度相符.
再将x=175代入函数式,即,用计算器求得y≈63.98.
因为≈1.22>1.2,所以,这个男生偏胖.
【总结升华】由于本题没有给出函数模型,因此需要根据题目中的有关数据描绘出基本草图,然后根据直观性,去和已学过的有关函数图象对照、比较,由此猜测函数模型.在解此类问题的过程中,首先需要在实际的情境中去理解、分析所给的一系列数据,舍弃与解题无关的因素,抽象转化为数学模型.
【巩固练习】
1.某学校开展研究性学习活动,一组同学获得了下面的一组实验数据:
1.99
3
4
5.1
6.12
1.5
4.04
7.5
12
18.01
现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
A. B. C. D.
2.一辆汽车在某段路程中的行驶路程s关于时间t变化的图象如下图所示,那么图象所应对的函数模型是( )
A.分段函数 B.二次函数 C.指数函数 D.对数函数
3.某厂日产手套总成本y(元)与手套日产量x(副)的函数解析式为y=5x+4000,而手套出厂价格为每副10元,则该厂为了不亏本,日产手套至少为( )
A.200副 B.400副 C.600副 D.800副
4.(2018 四川广元模拟)某城区按以下规定收取水费:若每月和水不超过20 m3,则每立方米水费按2元收取;若超过20 m3,则超过的部分按每立方米3元收取,如果某户居民在某月所交水费的平均价为每立方米2.20元,则这户居民这月共用水( )
A.46 m3 B.44 m3 C.26 m3 D.25 m3
5.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系(a,b,c是常数),右图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
/
6.一高为H、满缸水量为V的鱼缸截面如右图所示,其底部破了一个小洞,缸中水从洞中流出.若鱼缸水深为h时的水的体积为v,则函数v=f (h)的大致图象可能是下图中四个选项中的( )
/
7.下表列出了一项试验的统计数据,表示将皮球从高h米处落下,弹跳高度d与下落高度h的关系:
h(米)
50
80
100
150
…
d(米)
25
40
50
75
…
写出一个能表示这种关系的式子为________.
8.某工厂生产某种产品的固定成本为2000万元,并且每生产一单位产品,成本增加10万元,又知总收入k(万元)是单位产品数Q的函数,,则总利润L(Q)的最大值是________.
9.某种细菌经30分钟繁殖为原来的2倍,且知该细菌的繁殖规律为y=ekt,其中k为常数,t表示时间(单位:小时),y表示细菌个数,则k=________,经过5小时,1个细菌能繁殖为________个.
10.已知某地今年年初拥有居民住房的总面积为a(单位:m2),其中有部分旧住房需要拆除.当地有关部门决定每年以当年年初住房面积的10%建设新住房,同事也拆除面积为b(单位:m2)的旧住房.
(Ⅰ)分别写出第一年末和第二年末的实际住房面积的表达式:
(Ⅱ)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)
11.(2018 山东模拟)已知某城市2017年底的人口总数为200元,假设此后该城市人口的年增长率 1%(不考虑其他因素).
(1)若经过x年该城市人口总数为y万,试写出y关于x的函数关系式;
(2)如果该城市人口总数达到210万,那么至少需要经过多少年(精确到1年)?
12.某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价x元与日销售量y件之间有如下关系:
x 45 50
y 27 12
(Ⅰ)确定x与y的一个一次函数关系式y=f(x);
(Ⅱ)若日销售利润为P元,根据(I)中关系写出P关于x的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
【答案与解析】
1.【答案】D
【解析】把的值分别代入四个函数式,结果最最近的就是。
2.【答案】A
【解析】 由图象知,在不同时段内,路程折线图不同,故对应的函数模型为分段函数.
3.分析:根据题意列出出/厂价格和成本之间的不等关系式:5x+4000≤10x,解出即可.
【答案】D
【解析】由5x+4000≤10x,解得x≥800,即日产手套至少800副时才不亏本.
故选D.
点评:主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解.
4.【答案】D
【解析】设他这个月共用了x立方米的水
20×2+(x-20)×3=2.2x
40+3x-60=2.2x
0.8x=20
x=25.
他这个月共用了25立方米的水.
故选:D.
5.【答案】3.75
【解析】由题意得解之得
∴,最佳加工时间应是p最高的时候,
当t=3.75时,p有最大值.故填3.75.
6.【答案】B
【解析】由鱼缸的形状可知,水的体积随h的减小,一开始减少得慢,后来又减少得快,然后再减少得慢.
7.【答案】
【解析】观察表中数据即可.
8.【答案】2500万元
【解析】 总利润L=总收入k-总支出(生产成本+固定成本).所以.故当Q=300时,总利润的最大值为2500万元.
9.【答案】2ln2 1024
【解析】 将代入,得,所以,k=2ln2,这时函数关系式为,令t=5(小时),得y=210=1024(个).
10.【解析】(Ⅰ)第1年末的住房面积.
第2年末的住房面积(a·-b)·-b=a·()2-b(1+)=1.21a-2.1b(m2).
(Ⅱ)第3年末的住房面积[a·()3-b(1+)]-b=a·()3-b[1++()2].
第4年末住房面积为a·()4-b[1++()2+()3].
第5年末住房面积为a·()5-b[1++()2+()3+()4]=1.15a-b=1.6a-6b
依题意可知,1.6a-6b=1.3a,解得b=,所以每年拆除的旧房面积为(m2).
11.【答案】(1);(2)5年
【解析】(1).
(2)令y=210,即,解得.
答:要经过5年该城市人口总数达到210万.
12.分析:(Ⅰ)设出y=f(x)的表达式,利用已知条件列出方程组求解即可得到函数的解析式;
(Ⅱ)若日销售利润为P元,根据(I)中关系直接写出P关于x的函数关系,然后利用二次函数闭区间的最值即可求解最大的日销售利润.
【答案】(Ⅰ)y=162-3x,且0≤x≤54;(Ⅱ)42元
【解析】(Ⅰ)因为f(x)为一次函数,设y=ax+b,解方程组
得a=-3,b=162,
故y=162-3x为所求的函数关系式,
又∵y≥0,∴0≤x≤54.
(Ⅱ)依题意得:
.
当x=42时,,
即销售单价为42元/件时,获得最大日销售利润.
点评:本题考查函数的模型的选择与应用,二次函数闭区间上的最值的求法,考查分析问题解决问题的能力.
