13.1.2 定理与证明 教案(表格式)
文档属性
| 名称 | 13.1.2 定理与证明 教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 55.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-12 00:00:00 | ||
图片预览


文档简介
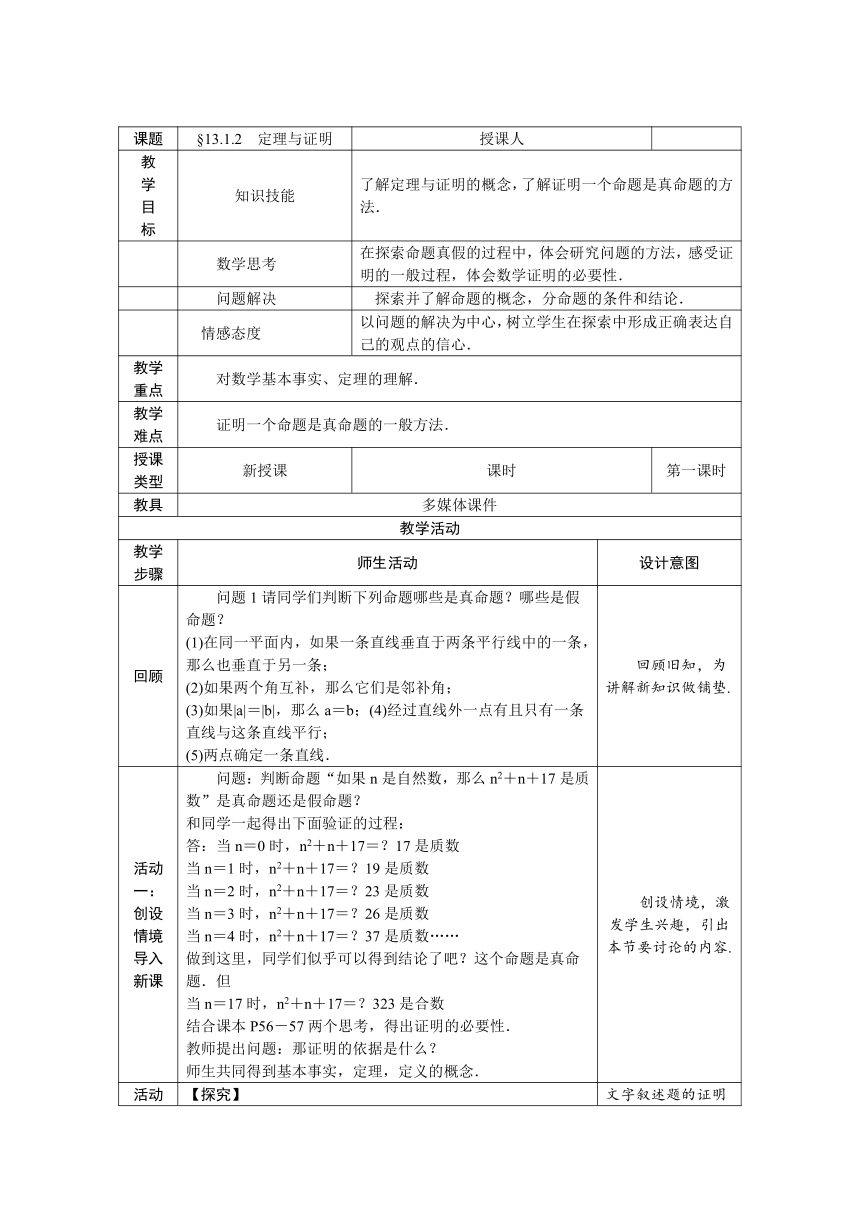
课题
§13.1.2 定理与证明
授课人
教
学
目
标
知识技能
了解定理与证明的概念,了解证明一个命题是真命题的方法.
数学思考
在探索命题真假的过程中,体会研究问题的方法,感受证明的一般过程,体会数学证明的必要性.
问题解决
探索并了解命题的概念,分命题的条件和结论.
情感态度
以问题的解决为中心,树立学生在探索中形成正确表达自己的观点的信心.
教学
重点
对数学基本事实、定理的理解.
教学
难点
证明一个命题是真命题的一般方法.
授课
类型
新授课
课时
第一课时
教具
多媒体课件
教学活动
教学
步骤
师生活动
设计意图
回顾
问题1请同学们判断下列命题哪些是真命题?哪些是假命题?
(1)在同一平面内,如果一条直线垂直于两条平行线中的一条,那么也垂直于另一条;
(2)如果两个角互补,那么它们是邻补角;
(3)如果|a|=|b|,那么a=b;(4)经过直线外一点有且只有一条直线与这条直线平行;
(5)两点确定一条直线.
回顾旧知,为讲解新知识做铺垫.
活动
一:
创设
情境
导入
新课
问题:判断命题“如果n是自然数,那么n2+n+17是质数”是真命题还是假命题?
和同学一起得出下面验证的过程:
答:当n=0时,n2+n+17=?17是质数
当n=1时,n2+n+17=?19是质数
当n=2时,n2+n+17=?23是质数
当n=3时,n2+n+17=?26是质数
当n=4时,n2+n+17=?37是质数……
做到这里,同学们似乎可以得到结论了吧?这个命题是真命题.但
当n=17时,n2+n+17=?323是合数
结合课本P56-57两个思考,得出证明的必要性.
教师提出问题:那证明的依据是什么?
师生共同得到基本事实,定理,定义的概念.
创设情境,激发学生兴趣,引出本节要讨论的内容.
活动
二:
实践
探究
交流
新知
【探究】
通过七年级的学习,我们已经知道如下各命题都是正确的,即都是公认的真命题:
两点确定一条直线
两点之间线段最短
过一点有且只有一条直线与已知直线垂直
过直线外一点有且只有一条直线与这条直线平行
……
有些命题可以从基本事实出发或其它真命题出发,用逻辑推理的方法判断它们是正确的,并且可以作为进一步判断其他命题真假的依据,这样的真命题叫做定理.
归纳:定理的作用不仅在于它揭示了客观事物的本质属性,而且可以作为进一步确认其他命题真假的依据.
探究证明:根据条件、定义以及基本事实、定理等,经过演绎推理,来判断一个命题是否正确,这样的推理过程叫做证明
例 如图13-1-,有下列三个条件:
图13-1-
①DE∥BC:②∠1=∠2;③∠B=∠C.
(1)若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题,请你都写出来;
(2)请你就其中的一个真命题给出推理过程.
解:(1)一共能组成2个命题,它们是:题设:①②,结论:③;题设:①③,结论:②;
(2)情况一题设:①②,结论:③;证明:如图,∵DE∥BC,∴∠1=∠B,∠2=∠C.又∵∠1=∠2,∴∠B=∠C;
情况二题设:①③,结论:②;证明:如图,∵DE∥BC,∴∠1=∠B,∠2=∠C.又∵∠B=∠C,∴∠1=∠2.
归纳总结:
证明的一般步骤:
第一步:根据题意画出图形;
第二部:根据命题的条件和结论,结合图形,写出已知、求证;
第三步:通过分析,找出证明的方法,写出证明过程.
在证明几何命题时,须注意以下几点:
1.明确题目的条件和结论;
2.证明过程中引用的根据(理由)与“定理的证明相同”;
3.证明过程中每一步结果所用的根据必须是取得这一结果的充分理由;
4.要防止利用未学过的定理来证明学过的命题,避免循环论证
文字叙述题的证明过程需要学生有所了解.
活动
三:
开放
训练
体现
应用
【应用举例】
例1 把下列定理改写成“如果……,那么……”的形式.并说出条件和结论
(1)全等三角形的对应边相等;
(2)等角的余角相等.
说明:这里主要是巩固定理也是命题,要求学生即要能把它改写成“如果……,那么……”形式,也要能分清定理的条件和结论.
例2 求证:在同一平面内,两直线同垂直于第三条直线,那么这两条直线平行.
说明:老师和学生一起,写出已知,求证,然后画出图形,再用已经学过的定理进行证明.
1.要求学生注意定理也是命题注意它的两个组成部分:条件和结论.
2.能证明一个较简单的命题是真命题.
【拓展提升】
[厦门中考] A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权.比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队(有且只有两个队)出线.小组赛结束后,如果A队没有全胜,那么A队的积分至少要几分才能保证一定出线?请说明理由.
【注:单循环比赛就是小组内的每一个队都要和其他队赛一场】
结合生活中的例子,发展学生的合情推理能力.
活动
四:
课堂
总结
反思
【当堂检测】
1.把下列定理改写成“如果……,那么……”的形式.并说出条件和结论.
(1)有两个角等于60度的三角形是等边三角形;
(2)有两个角的和是90°的三角形是直角三角形.
2.证明:邻补角的角平分线互相垂直.
3.在学习中,小明发现:当n=1,2,3时,n2-6n都是负数,于是小明猜想:当n为任意正整数时,n2-6n的值都是负数.小明的猜想正确吗?
图13-1-
4.如图13-1-所示,∠1=∠2,则AB∥CD,这个命题是真命题吗?若不是,请你添加一个条件,使它成为真命题,并说明理由.
回顾与反思
1.同学们想一想,今天学习了哪些知识?
2.为什么全等三角形的对应边相等、对应角相等?
布置作业,专题突破
课本P55练习第1,2题.
1.当堂检测,及时反馈学习效果,巩固命题的概念及构成.
2.回顾与反思,起到把握整节课重要概念的作用.
【知识网络】
命题→真命题→定理(基本事实)→证明一个命题是真命题的依据
探索问题的方法
1.验证等;
2.说明验证的合理性(证明)
框架图式总结,更容易形成知识网络.
【教学反思】
①[授课流程反思]
A.新课导入□ B.情景导入□
基本事实、定理、定义均是命题,都是证明一个命题是真命题的依据,可以从命题的概念得到这三个概念,并从实例出发说明证明的必要性.证明一个命题是真命题的一般步骤可以让学生有所了解,不必要求学生掌握,在书写证明过程是要言必有据.
②[讲授效果反思]
A.重点□ B.难点□ C.易错点□
举反例说明一个命题是假命题是一个难点,教学时要帮助学困生,关注他们在这方面的不足.证明过程的书写是一个较为长期的训练过程,不期望一节课上学生就能很好地掌握.
③[师生互动反思]
学生根据定理的内容画出相应的图形会有较大的困难,师生共同完成.
④[习题反思]
好题题号__________________________________________
错题题号__________________________________________
教学反思进一步提升教师教学能力.
