2019年全国各地高考真题分类——光学部分
文档属性
| 名称 | 2019年全国各地高考真题分类——光学部分 | 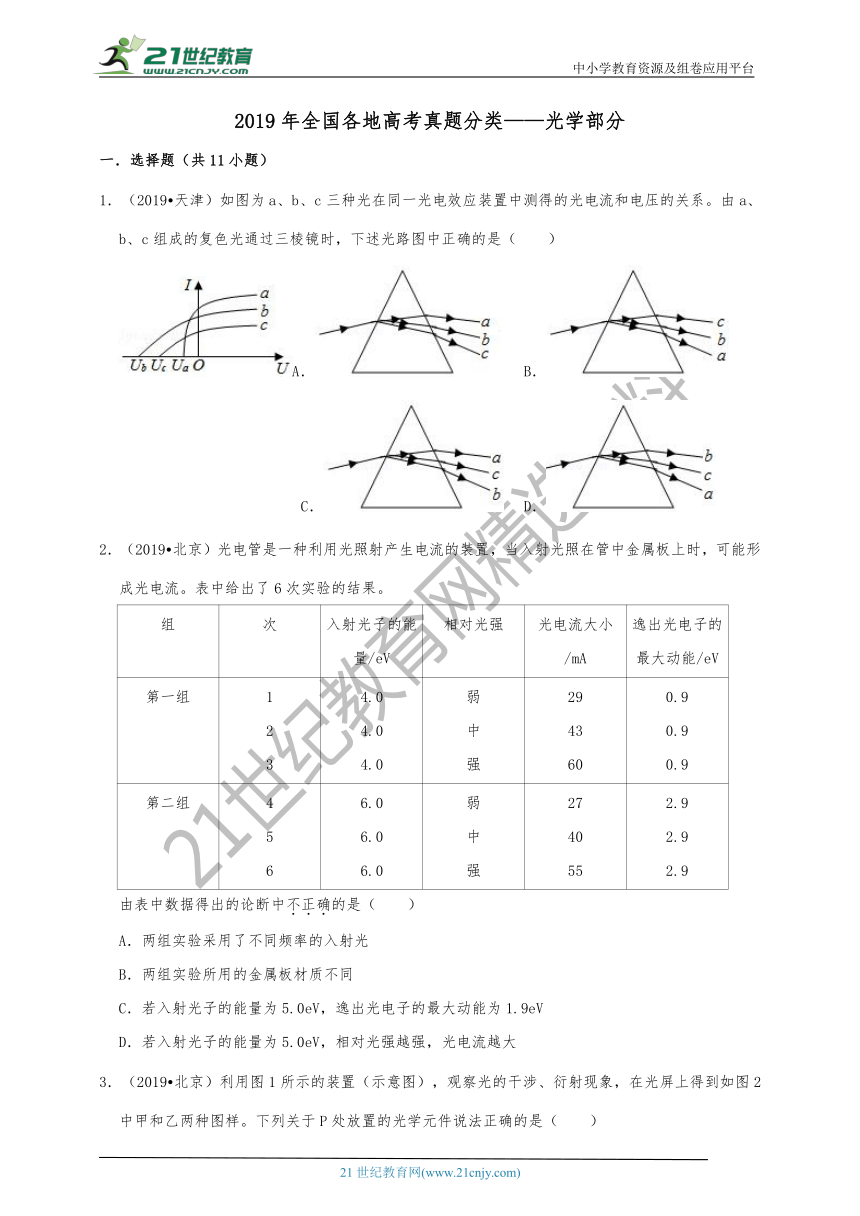 | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-07-12 17:29:44 | ||
图片预览





文档简介
2019年全国各地高考真题分类——光学部分
一.选择题(共11小题)
1.(2019?天津)如图为a、b、c三种光在同一光电效应装置中测得的光电流和电压的关系。由a、b、c组成的复色光通过三棱镜时,下述光路图中正确的是( )
A. B.
C. D.
2.(2019?北京)光电管是一种利用光照射产生电流的装置,当入射光照在管中金属板上时,可能形成光电流。表中给出了6次实验的结果。
组
次
入射光子的能量/eV
相对光强
光电流大小/mA
逸出光电子的最大动能/eV
第一组
1
2
3
4.0
4.0
4.0
弱
中
强
29
43
60
0.9
0.9
0.9
第二组
4
5
6
6.0
6.0
6.0
弱
中
强
27
40
55
2.9
2.9
2.9
由表中数据得出的论断中不正确的是( )
A.两组实验采用了不同频率的入射光
B.两组实验所用的金属板材质不同
C.若入射光子的能量为5.0eV,逸出光电子的最大动能为1.9eV
D.若入射光子的能量为5.0eV,相对光强越强,光电流越大
3.(2019?北京)利用图1所示的装置(示意图),观察光的干涉、衍射现象,在光屏上得到如图2中甲和乙两种图样。下列关于P处放置的光学元件说法正确的是( )
A.甲对应单缝,乙对应双缝
B.甲对应双缝,乙对应单缝
C.都是单缝,甲对应的缝宽较大
D.都是双缝,甲对应的双缝间距较大
4.(2019?上海)泊松亮斑是光的( )
A.干涉现象,说明光有波动性 B.衍射现象,说明光有波动性
C.干涉现象,说明光有粒子性 D.衍射现象,说明光有粒子性
5.(2018?北京)用双缝干涉实验装置得到白光的干涉条纹,在光源与单缝之间加上红色滤光片后( )
A.干涉条纹消失 B.彩色条纹中的红色条纹消失
C.中央条纹变成暗条纹 D.中央条纹变成红色
6.(2018?天津)氢原子光谱在可见光区域内有四条谱线Hα、Hβ、Hγ和Hδ,都是氢原子中电子从量子数n>2的能级跃迁到n=2的能级时发出的光,它们在真空中的波长由长到短,可以判定( )
A.Hα对应的前后能级之差最小 B.同一介质对Hα的折射率最大
C.同一介质中Hδ的传播速度最大 D.用Hγ照射某一金属能发生光电效应,则Hβ也一定能
7.(2018?新课标Ⅱ)用波长为300nm的光照射锌板,电子逸出锌板表面的最大初动能为1.28×10﹣19J,已知普朗克常量为6.63×10﹣34J?s,真空中的光速为3.00×108m?s﹣1,能使锌产生光电效应的单色光的最低频率约为( )
A.1×1014Hz B.8×1014Hz C.2×1015Hz D.8×1015Hz
8.(2017?天津)明代学者方以智在《阳燧倒影》中记载:“凡宝石面凸,则光成一条,有数棱则必有一面五色”,表明白光通过多棱晶体折射会发生色散现象.如图所示,一束复色光通过三棱镜后分解成两束单色光a、b,下列说法正确的是( )
A.若增大入射角i,则b光先消失
B.在该三棱镜中a光波长小于b光
C.a光能发生偏振现象,b光不能发生
D.若a、b光分别照射同一光电管都能发生光电效应,则a光的遏止电压低
9.(2017?北京)如图所示,一束可见光穿过平行玻璃砖后,变为a、b两束单色光.如果光束b是蓝光,则光束a可能是( )
A.红光 B.黄光 C.绿光 D.紫光
10.(2017?北京)2017年年初,我国研制的“大连光源”﹣﹣极紫外自由电子激光装置,发出了波长在100nm(1nm=10﹣9m)附近连续可调的世界上首个最强的极紫外激光脉冲,大连光源因其光子的能量大、密度高,可在能源利用、光刻技术、雾霾治理等领域的研究中发挥重要作用。
一个处于极紫外波段的光子所具有的能量可以电离一个分子,但又不会把分子打碎。据此判断,能够电离一个分子的能量约为(取普朗克常量h=6.6×10﹣34J?s,真空光速c=3×108m/s)( )
A.10﹣21J B.10﹣18J C.10﹣15J D.10﹣12J
11.(2017?北京)物理学原理在现代科技中有许多重要应用。例如,利用波的干涉,可将无线电波的干涉信号用于飞机降落的导航。如图所示,两个可发射无线电波的天线对称地固定于飞机跑道两侧,它们类似于杨氏干涉实验中的双缝。两天线同时都发出波长为λ1和λ2的无线电波。飞机降落过程中,当接收到λ1和λ2的信号都保持最强时,表明飞机已对准跑道。下列说法正确的是( )
A.天线发出的两种无线电波必须一样强 B.导航利用了λ1与λ2两种无线电波之间的干涉
C.两种无线电波在空间的强弱分布稳定 D.两种无线电波各自在空间的强弱分布完全重合
二.多选题(共7小题)
12.(2019?海南)对于钠和钙两种金属,其遏止电压Uc与入射光频率v的关系如图所示。用h、e分别表示普朗克常量和电子电荷量,则( )
A.钠的逸出功小于钙的逸出功
B.图中直线的斜率为
C.在得到这两条直线时,必须保证入射光的光强相同
D.若这两种金属产生的光电子具有相同的最大初动能,则照射到钠的光频率较高
13.(2018?浙江)处于较高能级的氢原子向较低能级跃迁时,能辐射出a、b两种可见光,a光照射某金属表面时有光电子逸出,b光照射该金属表面时没有光电子逸出,则( )
A.以相同的入射角射向一平行玻璃砖,a光的侧移量小于b光的
B.垂直入射到同一单缝衍射装置,a光的衍射中央亮条纹宽度小于b光的
C.a光和b光的频率之比可能是
D.a光子的动量大于b光子的
14.(2017?浙江)a、b是两种单色光,其光子能量分别为?a和?b,且=k,则( )
A.则a、b的光子动量之比=1:k
B.若a、b入射到同一双缝干涉装置上,则相邻亮条纹的间距之比=1:k
C.若a、b都能使某种金属发生光电效应,则光电子最大初动能之差Eka﹣Ekb=?b(k﹣1)
D.若a、b是由处于同一激发态的原子跃迁到a态和b态时产生的,则a、b两态能级之差Ea﹣Eb=?b(k﹣1)
15.(2017?海南)如图,空气中有两块材质不同、上下表面平行的透明玻璃板平行放置;一细光束从空气中以某一角度θ(0<θ<90°)入射到第一块玻璃板的上表面。下列说法正确的是( )
A.在第一块玻璃板下表面一定有出射光
B.在第二块玻璃板下表面一定没有出射光
C.第二块玻璃板下表面的出射光方向一定与入射光方向平行
D.第二块玻璃板下表面的出射光一定在入射光延长线的左侧
E.第一块玻璃板下表面的出射光线一定在入射光延长线的右侧
16.(2017?海南)三束单色光1、2和3的波长分别为λ1、λ2和λ3(λ1>λ2>λ3)。分别用这三束光照射同一种金属。已知用光束2照射时,恰能产生光电子。下列说法正确的是( )
A.用光束1照射时,不能产生光电子
B.用光束3照射时,不能产生光电子
C.用光束2照射时,光越强,单位时间内产生的光电子数目越多
D.用光束2照射时,光越强,产生的光电子的最大初动能越大
17.(2017?新课标Ⅲ)在光电效应实验中,分别用频率为va、vb的单色光a、b照射到同种金属上,测得相应的遏止电压分别为Ua和Ub、光电子的最大初动能分别为Eka和Ekb,h为普朗克常量。下列说法正确的是( )
A.若va>vb,则一定有Ua<Ub B.若va>vb,则一定有Eka>Ekb
C.若Ua<Ub,则一定有Eka<Ekb D.若va>vb,则一定有hva﹣Eka>hvb﹣Ekb
18.(2017?浙江)图中给出了“用双缝干涉测量光的波长”实验示意图,双缝S1和S2间距为0.80mm,双缝到屏的距离为0.80m,波长为500nm的单色平行光垂直入射到双缝S1和S2上,在屏上形成干涉条纹,中心轴线OO′上方第1条亮纹中心位置在P1处,第3条亮纹中心位置在P2处,现有1号、2号虫子分别从S1和S2出发以相同速度沿垂直屏方向飞行,1号虫子到达屏后,沿屏直线爬行到P1,2号虫子到达屏后,沿屏直线爬行到P2,假设两条虫子爬行速率均为10﹣3m/s,正确的是( )
A.1号虫子运动路程比2号短
B.两只虫子运动的时间差为0.2s
C.两只虫子运动的时间差为1.0s
D.已知条件不够,两只虫子运动时间差无法计算
三.填空题(共4小题)
19.(2019?江苏)将两支铅笔并排放在一起,中间留一条狭缝,通过这条狭缝去看与其平行的日光灯,能观察到彩色条纹,这是由于光的 (选填“折射”“干涉”或“衍射”)。当缝的宽度 (选填“远大于”或“接近”)光波的波长时,这种现象十分明显。
20.(2018?江苏)光电效应实验中,用波长为λ0的单色光A照射某金属板时,刚好有光电子从金属表面逸出。当波长为的单色光B照射该金属板时,光电子的最大初动能为 ,A、B两种光子的动量之比为 。(已知普朗克常量为h、光速为c)
21.(2018?新课标Ⅰ)如图,△ABC为一玻璃三棱镜的横截面,∠A=30°,一束红光垂直AB边射入,从AC边上的D点射出。其折射角为60°,则玻璃对红光的折射率为 。若改用蓝光沿同一路径入射,则光线在D点射出时的折射角 (填“小于”“等于”或“大于”)60°。
22.(2017?江苏)质子(H)和α粒子(He)被加速到相同动能时,质子的动量 (选填“大于”、“小于”或“等于”)α粒子的动量,质子和α粒子的德布罗意波波长之比为 .
四.实验题(共1小题)
23.(2016?江苏)(1)杨氏干涉实验证明光的确是一种波,一束单色光投射在两条相距很近的狭缝上,两狭缝就成了两个光源,它们发出的光波满足干涉的必要条件,则两列光的 相同.如图所示,在这两列光波相遇的区域中,实线表示波峰,虚线表示波谷,如果放置光屏,在 (选填“A”、“B”或“C”)点会出现暗条纹.
(2)在上述杨氏干涉试验中,若单色光的波长λ=5.89×10﹣7m,双缝间的距离d=1mm,双缝到屏的距离l=2m.求第1个亮光条纹到第11个亮条纹的中心间距.
五.计算题(共13小题)
24.(2019?江苏)在“焊接”视网膜的眼科手术中,所用激光的波长λ=6.4×10﹣7m,每个激光脉冲的能量E=1.5×10﹣2J.求每个脉冲中的光子数目。(已知普朗克常量h=6.63×10﹣34J?s,光速c=3×108m/s,计算结果保留一位有效数字)
25.(2019?江苏)如图所示,某L形透明材料的折射率n=2.现沿AB方向切去一角,AB与水平方向的夹角为θ.为使水平方向的光线射到AB面时不会射入空气,求θ的最大值。
26.(2019?新课标Ⅲ)如图,直角三角形ABC为一棱镜的横截面,∠A=90°,∠B=30°.一束光线平行于底边BC射到AB边上并进入棱镜,然后垂直于AC边射出。
(i)求棱镜的折射率;
(ii)保持AB边上的入射点不变,逐渐减小入射角,直到BC边上恰好有光线射出。求此时AB边上入射角的正弦。
27.(2019?新课标Ⅰ)如图,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3m。距水面4m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin53°=0.8)。已知水的折射率为。
(i)求桅杆到P点的水平距离;
(ⅱ)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍照射在桅杆顶端,求船行驶的距离。
28.(2018?全国)如图,玻璃柱的横截面为半径R=20.0cm的半圆,O点为圆心。光屏CD紧靠在玻璃柱的右侧且与截面底边MN垂直。一光束沿半径方向射向O点,光束和MN的夹角为θ,在光屏CD上出现两个光斑。已知玻璃的折射率为n=。
(1)若θ=60°,求两个光斑间的距离
(2)屏上两个光斑间的距离会随θ大小的变化而改变,求两光斑间的最短距离。
29.(2018?海南)如图,由透明介质构成的半球壳的内外表面半径分别为R和R.一横截面半径为R的平行光束入射到半球壳内表面,入射方向与半球壳的对称轴平行,所有的入射光线都能从半球壳的外表面射出。已知透明介质的折射率为n=.求半球壳外表面上有光线射出区域的圆形边界的半径。不考虑多次反射。
30.(2018?新课标Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°.一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出,EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(i)求出射光相对于D点的入射光的偏角;
(ii)为实现上述光路,棱镜折射率的取值应在什么范围?
31.(2018?新课标Ⅲ)如图,某同学在一张水平放置的白纸上画了一个小标记“?”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点做AC边的垂线交AC于F.该同学在D点正上方向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点做AB边的垂线交直线DF于E;DE=2cm,EF=1cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
32.(2017?江苏)人的眼球可简化为如图所示的模型,折射率相同、半径不同的两个球体共轴,平行光束宽度为D,对称地沿轴线方向射入半径为R的小球,会聚在轴线上的P点.取球体的折射率为,且D=R,求光线的会聚角α.(示意图未按比例画出)
33.(2017?新课标Ⅰ)如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R.已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)。求该玻璃的折射率。
34.(2017?新课标Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示.容器右侧内壁涂有反光材料,其他内壁涂有吸光材料.在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率.
35.(2017?新课标Ⅲ)如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线).已知玻璃的折射率为1.5.现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线).求:
(i)从球面射出的光线对应的入射光线到光轴距离的最大值;
(ii)距光轴的入射光线经球面折射后与光轴的交点到O点的距离.
36.(2016?新课标Ⅰ)如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0m.从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为.
(i)求池内的水深;
(ii)一救生员坐在离池边不远处的高凳上,他的眼睛到地面的高度为2.0m.当他看到正前下方的点光源A时,他的眼睛所接受的光线与竖直方向的夹角恰好为45°.求救生员的眼睛到池边的水平距离(结果保留1位有效数字).
2019年全国各地高考真题分类——光学部分
参考答案与试题解析
一.选择题(共11小题)
C.若入射光子的能量为5.0eV,根据光电效应方程Ek=hv﹣W,可得逸出光电子的最大动能为Ek=5.0eV﹣3.1eV=1.9eV,故C正确;
D.由表格中的数据可知,在产生光电效应的前提下,对同种频率的入射光而言,入射光的强度越大,光电流越大,所以若入射光子的能量为5.0eV,相对光强越强,光电流越大,故D正确。
本题选不正确的,故选:B。
3.【解答】解:干涉条纹在光屏上观察到的图案是间距相等的条纹图象,而衍射条纹中,中间的亮纹的宽度最大,向两边渐渐减小,
因此甲对应单缝,乙对应双缝,故A正确,BCD错误。
故选:A。
4.【解答】解:泊松亮斑是光的衍射现象形成的,而光的衍射现象说明光的波动性;故B正确,ACD错误。
故选:B。
5.【解答】解:A、在双缝中,仍是频率相同的红光,因此能发生干涉现象,故A错误;
B、由于只有红光干涉条纹,因此不会出现彩色条纹,也没有彩色条纹中的红色条纹消失现象,故B错误;
C、在中央条纹,满足光程差为零,则是明条纹,并不变成暗条纹,故C错误;
D、得到白光的干涉条纹后,在光源与单缝之间加上红色滤光片,在双缝中的,由于红光的频率相同,则能发生干涉,但不是彩色条纹,而是明暗相间的红色条纹,故D正确。
故选:D。
6.【解答】解:A、四条谱线Hα、Hβ、Hγ和Hδ,在真空中的波长由长到短,根据,可知,四条谱线Hα、Hβ、Hγ和Hδ,的频率是由低到高;那么它们的能量也是由小到大,
而△E=Em﹣En=hγ,则Hα对应的前后能级之差最小,故A正确;
B、当在同一介质,由于Hδ,能量最大,那么其的折射率也最大,而对Hα的折射率最小,故B错误;
C、在同一介质中,Hδ的折射率最大,由v=,可知,其传播速度最小,故C错误;
D、若用Hγ照射某一金属能发生光电效应,由于Hβ的能量小于Hγ,即Hβ的频率小于Hγ,依据光电效应发生条件,其入射频率不小于极限频率则Hβ不一定能,故D错误;
故选:A。
7.【解答】解:根据光电效应方程:EKm=hγ﹣W0
光速、波长、频率之间关系为:γ=
将数据,代入上式,则有:W0=hγ﹣EKm=6.63×10﹣34J?s×s﹣1﹣1.28×10﹣19J=5.35×10﹣19J
根据逸出功W0=hγ0,得:
γ0==≈8×1014 Hz;
故选:B。
8.【解答】解:A、根据折射率定义公式n=,从空气斜射向玻璃时,入射角相同,光线a对应的折射角较大,故光线a的折射率较小,即na<nb,若增大入射角i,在第二折射面上,则两光的入射角减小,依据光从光密介质进入光疏介质,且入射角大于或等于临界角时,才能发生光的全反射,因此它们不会发生光的全反射,故A错误;
B、根据折射率定义公式n=,从空气斜射向玻璃时,入射角相同,光线a对应的折射角较大,故光线a的折射率较小,即na<nb,则在真空中a光波长大于b光波长,故B错误;
C、只要是横波,均能发生偏振现象,若a光能发生偏振现象,b光一定能发生,故C错误;
D、a光折射率较小,则频率较小,根据E=hγ,则a光光子能量较小,则a光束照射逸出光电子的最大初动能较小,根据qUc=,则a光的遏止电压低,故D正确;
故选:D。
9.【解答】解:光从空气斜射到玻璃,因为玻璃上下表面平行,当第二次折射时折射光线与第一次折射入射光线平行。由于折射率不同,a光偏折较大,b光偏折较小。所以此玻璃对a光的折射率大于对b光的折射率,所以a的频率大于b的频率,给出的各色光中频率大于蓝光的只有紫光,故D正确,ABC错误。
故选:D。
10.【解答】解:能够电离一个分子的能量为E==J=1.98×10﹣18J,故B正确,A、C、D错误。
故选:B。
11.【解答】解:A、干涉要求两波源的频率相同,而强度没有要求,故A错误。
B、由于无线电波以光速传播,根据知,波长不同,频率不同,所以两种无线电波之间不会发生干涉,故B错误。
C、空间中某点加强与减弱取决于到两波源的距离差为半波长的奇、偶数倍。所以两种电波的波峰与波峰叠加最强分布是固定的,而且λ1≠λ2,所以无线电波各自在空间的强弱分布不重合,不过中垂线都是加强点,故C正确,D错误。
故选:C。
二.多选题(共7小题)
12.【解答】解:A、根据光电效应方程得:
Ekm=hγ﹣W0=hγ﹣hγ0
又Ekm=eUC
解得:UC=γ﹣=γ﹣;
当遏止电压为0时,对应的频率为金属的极限频率,结合图可知钠的极限频率小,则钠的逸出功小。故A正确;
B、由UC=γ﹣知U0﹣γ图线的斜率k=,故B正确;
C、由UC=γ﹣知图线的特点与光的强度无关。故C错误;
D、钠的逸出功小,结合Ekm=hγ﹣W0可知,若这两种金属产生的光电子具有相同的最大初动能,则照射到钠的光频率较小。故D错误
故选:AB。
13.【解答】解:A、根据题意可知a光频率低于b光频率,玻璃砖对a光的折射率大于对b光的折射率,b光的折射率较小,以相同角度斜射到同一玻璃板透过平行表面后,b光的折射角较大,所以b光侧移量小,即a光的侧移量大于b光的,故A错误;
B、频率越大,波长越小,通过同一单缝衍射装置时,中央亮条纹宽度越小,故B正确;
C、a光的频率大,故频率之比不可能为,故C错误;
D、频率越大,波长越小,即λa<λb,根据可知pa>pb,故D正确。
故选:BD。
14.【解答】解:A、光子的能量:?=hγ
所以两种光子能量分别为?a和?b,且=k,则:
光子的动量:p=
所以:.故A错误;
B、光子的波长:
双缝干涉装置上相邻亮条纹的间距:
所以:.故B正确;
C、根据光电效应方程可知,光电子的最大初动能:Ekm=hγ﹣W,其中W为金属的逸出功;
则:Eka﹣Ekb=hγa﹣hγb=?b(k﹣1)。故C正确;
D、若a、b是由处于同一激发态的原子跃迁到a态和b态时产生的,设初始激发态的能量为E0,则:?a=hγa=E0﹣Ea
所以:Ea=E0﹣?a
同理:Eb=E0﹣?b
则:Ea﹣Eb=?b﹣?a=﹣?b(k﹣1)。故D错误。
故选:BC。
15.【解答】解:A、光线从第一块玻璃板中的上表面射入,在第一块玻璃板中上表面的折射角和下表面的入射角相等,根据光的可逆原理可知,光在第一块玻璃板下表面一定有出射光,同理,在第二个玻璃板下表面也一定有出射光,故A正确,B错误。
C、因为光在玻璃板中的上表面的折射角和下表面的入射角相等,根据光的可逆原理知,从下表面出射光的折射角和开始在上表面的入射角相等,即两光线平行,所以第二块玻璃板下表面的出射光方向一定与入射光方向平行,故C正确。
D、根据光线在玻璃板中发生偏折,由于折射角小于入射角,可知第二块玻璃板下表面的出射光一定在入射光延长线的左侧,故D正确,E错误。
故选:ACD。
16.【解答】解:AB、依据波长与频率的关系:,因λ1>λ2>λ3,那么γ1<γ2<γ3;由于用光束2照射时,恰能产生光电子,因此用光束1照射时,不能产生光电子,而光束3照射时,一定能产生光电子,故A正确,B错误;
CD、用光束2照射时,光越强,单位时间内产生的光电子数目越多,而由光电效应方程:Ekm=hγ﹣W,可知,光电子的最大初动能与光的强弱无关,故C正确,D错误;
故选:AC。
17.【解答】解:AB、根据光电效应方程Ekm=hv﹣W0知,va>vb,逸出功相同,则Eka>Ekb,又Ekm=eUc,则Ua>Ub,故A错误,B正确。
C、根据Ekm=eUc知,若Ua<Ub,则一定有Eka<Ekb,故C正确。
D、逸出功W0=hv﹣Ekm,由于金属的逸出功相同,则有:hva﹣Eka=hvb﹣Ekb,故D错误。
故选:BC。
18.【解答】解:A、由题,结合干涉条纹的宽度公式:可知,该光的干涉条纹的宽度:x=m
第1条亮纹中心位置在P1处,所以:m
第3条亮纹中心位置在P2处,所以:m
所以1号虫子的路程为:;
2号虫子的路程为:,
则:=1.5×10﹣3﹣5×10﹣4﹣0.80×10﹣3=0.2×10﹣3m.故A正确;
BCD、两只虫子运动的时间差s.故B正确,CD错误
故选:AB。
三.填空题(共4小题)
19.【解答】解:将两支铅笔并排放在一起,中间留一条狭缝,通过这条狭缝去看与其平行的日光灯,能观察到彩色条纹,这是由于光的衍射产生的。
当缝的宽度与光波波长接近时,衍射现象非常明显。
故答案为:衍射,接近。
20.【解答】解:由题知,金属板的逸出功为为:
W0=hγ0=
当波长为的单色光B照射该金属板时,根据爱因斯坦光电效应方程得:
Ek=h﹣W0=
根据p=得A、B两种光子的动量之比为:
pA:pB=:λ0=1:2
故答案为:,1:2。
21.【解答】解:由下图可知,当红光进入玻璃三棱镜后,在AB界面上垂直进入,到达AC界面发生了折射现象,根据几何关系可得:入射角的大小为∠1=30°,又因为已知折射角的大小为γ=60°,
利用折射定律可解得:玻璃对红光的折射率。
若改用蓝光沿同一路径入射,在AB界面上仍是垂直进入,由几何关系可知,其入射角不变;当到达AC界面发生折射现象,由于蓝光的折射率比红光的折射率大,再利用折射定律,
在∠1=30°不变的情况下,由于折射率增加,可得出其折射角将增加,即:光线在D点射出时的折射角大于60°。
故答案为:;大于。
22.【解答】解:动能与动量的关系为:P=,
物质波的波长:λ=,
联立得到:∝,
质子(H)和α粒子(He)质量之比为1:4,故物质波的波长之比为2:1;
故答案为:小于,2:1.
四.实验题(共1小题)
23.【解答】解:(1)产生稳定干涉图样的必要条件是两束光的频率相同.A、B两点是波峰与波峰、波谷与波谷相遇的点,是振动加强点,出现明条纹,C点波峰与波谷相遇,振动减弱,出现暗条纹.
(2)相邻干涉条纹的间距为△x==×5.89×10﹣7m=1.178×10﹣3m
则第1个亮光条纹到第11个亮条纹的中心间距为 S=10△x=1.178×10﹣2m
故答案为:(1)频率,C.(2)第1个亮光条纹到第11个亮条纹的中心间距为1.178×10﹣2m.
五.计算题(共13小题)
24.【解答】解:光子的能量为:?==J=3.1×10﹣19J。
每个脉冲中的光子数目为:n=≈5×1016个
答:每个脉冲中的光子数目为5×1016个
25.【解答】解:当光线在AB面上刚好发生全反射时θ最大,设全反射临界角为C,则sinC==
可得 C=30°
根据几何关系有 C+θ=90°
可得 θ=60°
答:θ的最大值是60°。
26.【解答】解:(i)光路图及相关量如图所示。
光束在AB边上折射,由折射定律得:
①
式中n是棱镜的折射率。由几何关系可知:α+β=60° ②
由几何关系和反射定律得:β=β′=∠B ③
联立①②③式,并代入i=60°得:n=④
(ii)设改变后的入射角为i′,折射角为α′,由折射定律得:⑤
依题意,光束在BC边上的入射角为全反射的临界角θc,且:sinθc=⑥
由几何关系得:θc═α'+30° ⑦
由④⑤⑥⑦式得入射角的正弦为:sini′=⑧
答:(i)棱镜的折射率为;
(ii)AB边上入射角的正弦为。
27.【解答】解:(i)设光束从水面射出的点到桅杆的水平距离为x1,到P点的水平距离为x2.桅杆的高度为h1,P点处水深为h2.激光束在水中与竖直方向的夹角为θ。
由几何关系有:
=tan53°…①
=tanθ…②
由折射定律有:n=…③
设桅杆到P点的水平距离为x,则:x=x1+x2…④
联立①②③④并代入数据解得:x=7m…⑤
(ii)设激光束在水中与竖直方向的夹角为45°时,从水面出射的方向与竖直方向的夹角为i′。
由折射定律有:n=…⑥
设船向左行驶的距离为x′,此时光束从水面射出的点到桅杆的水平距离为x1′,到P点的水平距离为x2′,则
x1′+x2′=x′+x…⑦
=tani′…⑧
=tan45°…⑨
联立⑤⑥⑦⑧⑨并代入数据解得:x′=(6﹣3)m≈5.5m
答:
(i)桅杆到P点的水平距离是7m;
(ⅱ)船行驶的距离是5.5m。
28.【解答】解:(1)光束在MN界面上一部分反射,设反射光与光屏CD的交点为C,另一部分折射,设折射光与光屏的交点为D,入射角为r,折射角为i,光路图如图所示,由几何关系得:r=90°﹣θ=30°
得:LCN==R
根据折射定律得 n=
可得,i=60°
则LDN==R
所以两个光斑间的距离 LCD=LCN+LDN=R=cm
(2)屏上两个光斑间的距离会随θ的减小而变短,当光线在MN就要发生全反射时,两光斑间距离最短,由临界角公式sinC=得:
sinC=
tanC===
所以两光斑间的最短距离 Lmin=
联立解得 Lmin=20cm
答:
(1)若θ=60°,两个光斑间的距离是cm。
(2)屏上两个光斑间的距离会随θ大小的变化而改变,两光斑间的最短距离是20cm。
29.【解答】解:设光从半球壳内表面边沿上的A点入射,入射角为90°(全反射临界角也为α),然后在半球壳外表面内侧的B点发生折射,入射角为β,如图所示。
由全反射临界角的定义得 1=nsinα①
由正弦定理得
=②
OD为对称思,设∠BOD=γ,由几何关系可知
γ=﹣(α﹣β)③
设B点到OD的距离为r,即为所求的半球壳外表面上有光线射出区域的圆形边界的半径,由几何关系有
r=Rsinγ④
由①②③④及题给数据解得 r=R
答:半球壳外表面上有光线射出区域的圆形边界的半径为R。
30.【解答】解:(i)由于D是CG的中点,GE⊥AC,根据几何关系可得:光束在D点发生折射时的折射角为γD=30°;
那么,根据几何关系可得:在E点的入射角、反射角均为γD+30°=60°;在F点的入射角为αF=30°;
那么,设入射角为αD,可得:折射角γF=αD,故出射光相对于D点的入射光的偏角为60°﹣αD+γF=60°;
(ii)由E点反射角为60°可得:EF∥BC;
故根据D点折射角为γD=30°,在F点的入射角为αF=30°可得:棱镜折射率;
根据光束在E点入射角为60°,发生全反射可得:,故棱镜折射率的取值范围为;
答:(i)出射光相对于D点的入射光的偏角为60°;
(ii)为实现上述光路,棱镜折射率的取值范围为。
31.【解答】解:连接DO,点E是三角形AOD的垂心,DE=2cm,EF=1cm,说明三角形OAD是等边三角形,点E也是重心、中心,故画出光路图,如图所示:
故入射角为60°,折射角为30°,故折射率为:
n==;
答:三检镜的折射率为。
32.【解答】解:设入射角为i.由几何关系得:sini==,
解得:i=45°
由折射定律有:n=,
解得折射角为:r=30°
且由几何关系有:i=r+,
解得:α=30°
答:光线的会聚角α是30°.
33.【解答】解:由题意,结合光路的对称性与光路可逆可知,与入射光相对于OC轴对称的出射光线一定与入射光线平行,所以从半球面射入的光线经折射后,将在圆柱体底面中心C点反射,如图:
设光线在半球处的入射角为i,折射光线的折射角为r,则:
sini=nsinr…①
由正弦定理得:=…②
由几何关系可知,入射点的法线与OC之间的夹角也等于i,该光线与OC之间的距离:L=0.6R
则:sini=…③
由②③得:sinr=
由①③④得:n=≈1.43
答:该玻璃的折射率为1.43。
34.【解答】解:设从光源发出的光直接射到D点的光线的入射角为i1,折射角为γ1,在剖面内做光源相对于镜面的对称点C,连接CD,交镜面与E点,由光源射向E点的光线反射后由ED射向D点,设入射角为i2,折射角为γ2,如图;
设液体的折射率为n,由折射定律:
nsini1=sinγ1
nsini2=sinγ2
由题意:γ1+γ2=90°
联立得:
由图中几何关系可得:;
联立得:n=1.55
答:该液体的折射率为1.55.
35.【解答】解:(i)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l.
i=ic
设n是玻璃的折射率,由全反射临界角的定义有
nsinic=l
由几何关系有
sini=
联立可得:l=R
(ii)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有
nsini1=sinr1
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有
由几何关系有
∠C=r1﹣i1
sini1=
联立可得:OC=R≈2.74R.
答:(i)从球面射出的光线对应的入射光线到光轴距离的最大值为;
(ii)距光轴的入射光线经球面折射后与光轴的交点到O点的距离2.74R.
36.【解答】解:(i)光由A射向B点发生全反射,光路如图所示.
图中入射角θ等于临界角C,则有
sinθ==
由题,=3m,由几何关系可得:
=4m
一.选择题(共11小题)
1.(2019?天津)如图为a、b、c三种光在同一光电效应装置中测得的光电流和电压的关系。由a、b、c组成的复色光通过三棱镜时,下述光路图中正确的是( )
A. B.
C. D.
2.(2019?北京)光电管是一种利用光照射产生电流的装置,当入射光照在管中金属板上时,可能形成光电流。表中给出了6次实验的结果。
组
次
入射光子的能量/eV
相对光强
光电流大小/mA
逸出光电子的最大动能/eV
第一组
1
2
3
4.0
4.0
4.0
弱
中
强
29
43
60
0.9
0.9
0.9
第二组
4
5
6
6.0
6.0
6.0
弱
中
强
27
40
55
2.9
2.9
2.9
由表中数据得出的论断中不正确的是( )
A.两组实验采用了不同频率的入射光
B.两组实验所用的金属板材质不同
C.若入射光子的能量为5.0eV,逸出光电子的最大动能为1.9eV
D.若入射光子的能量为5.0eV,相对光强越强,光电流越大
3.(2019?北京)利用图1所示的装置(示意图),观察光的干涉、衍射现象,在光屏上得到如图2中甲和乙两种图样。下列关于P处放置的光学元件说法正确的是( )
A.甲对应单缝,乙对应双缝
B.甲对应双缝,乙对应单缝
C.都是单缝,甲对应的缝宽较大
D.都是双缝,甲对应的双缝间距较大
4.(2019?上海)泊松亮斑是光的( )
A.干涉现象,说明光有波动性 B.衍射现象,说明光有波动性
C.干涉现象,说明光有粒子性 D.衍射现象,说明光有粒子性
5.(2018?北京)用双缝干涉实验装置得到白光的干涉条纹,在光源与单缝之间加上红色滤光片后( )
A.干涉条纹消失 B.彩色条纹中的红色条纹消失
C.中央条纹变成暗条纹 D.中央条纹变成红色
6.(2018?天津)氢原子光谱在可见光区域内有四条谱线Hα、Hβ、Hγ和Hδ,都是氢原子中电子从量子数n>2的能级跃迁到n=2的能级时发出的光,它们在真空中的波长由长到短,可以判定( )
A.Hα对应的前后能级之差最小 B.同一介质对Hα的折射率最大
C.同一介质中Hδ的传播速度最大 D.用Hγ照射某一金属能发生光电效应,则Hβ也一定能
7.(2018?新课标Ⅱ)用波长为300nm的光照射锌板,电子逸出锌板表面的最大初动能为1.28×10﹣19J,已知普朗克常量为6.63×10﹣34J?s,真空中的光速为3.00×108m?s﹣1,能使锌产生光电效应的单色光的最低频率约为( )
A.1×1014Hz B.8×1014Hz C.2×1015Hz D.8×1015Hz
8.(2017?天津)明代学者方以智在《阳燧倒影》中记载:“凡宝石面凸,则光成一条,有数棱则必有一面五色”,表明白光通过多棱晶体折射会发生色散现象.如图所示,一束复色光通过三棱镜后分解成两束单色光a、b,下列说法正确的是( )
A.若增大入射角i,则b光先消失
B.在该三棱镜中a光波长小于b光
C.a光能发生偏振现象,b光不能发生
D.若a、b光分别照射同一光电管都能发生光电效应,则a光的遏止电压低
9.(2017?北京)如图所示,一束可见光穿过平行玻璃砖后,变为a、b两束单色光.如果光束b是蓝光,则光束a可能是( )
A.红光 B.黄光 C.绿光 D.紫光
10.(2017?北京)2017年年初,我国研制的“大连光源”﹣﹣极紫外自由电子激光装置,发出了波长在100nm(1nm=10﹣9m)附近连续可调的世界上首个最强的极紫外激光脉冲,大连光源因其光子的能量大、密度高,可在能源利用、光刻技术、雾霾治理等领域的研究中发挥重要作用。
一个处于极紫外波段的光子所具有的能量可以电离一个分子,但又不会把分子打碎。据此判断,能够电离一个分子的能量约为(取普朗克常量h=6.6×10﹣34J?s,真空光速c=3×108m/s)( )
A.10﹣21J B.10﹣18J C.10﹣15J D.10﹣12J
11.(2017?北京)物理学原理在现代科技中有许多重要应用。例如,利用波的干涉,可将无线电波的干涉信号用于飞机降落的导航。如图所示,两个可发射无线电波的天线对称地固定于飞机跑道两侧,它们类似于杨氏干涉实验中的双缝。两天线同时都发出波长为λ1和λ2的无线电波。飞机降落过程中,当接收到λ1和λ2的信号都保持最强时,表明飞机已对准跑道。下列说法正确的是( )
A.天线发出的两种无线电波必须一样强 B.导航利用了λ1与λ2两种无线电波之间的干涉
C.两种无线电波在空间的强弱分布稳定 D.两种无线电波各自在空间的强弱分布完全重合
二.多选题(共7小题)
12.(2019?海南)对于钠和钙两种金属,其遏止电压Uc与入射光频率v的关系如图所示。用h、e分别表示普朗克常量和电子电荷量,则( )
A.钠的逸出功小于钙的逸出功
B.图中直线的斜率为
C.在得到这两条直线时,必须保证入射光的光强相同
D.若这两种金属产生的光电子具有相同的最大初动能,则照射到钠的光频率较高
13.(2018?浙江)处于较高能级的氢原子向较低能级跃迁时,能辐射出a、b两种可见光,a光照射某金属表面时有光电子逸出,b光照射该金属表面时没有光电子逸出,则( )
A.以相同的入射角射向一平行玻璃砖,a光的侧移量小于b光的
B.垂直入射到同一单缝衍射装置,a光的衍射中央亮条纹宽度小于b光的
C.a光和b光的频率之比可能是
D.a光子的动量大于b光子的
14.(2017?浙江)a、b是两种单色光,其光子能量分别为?a和?b,且=k,则( )
A.则a、b的光子动量之比=1:k
B.若a、b入射到同一双缝干涉装置上,则相邻亮条纹的间距之比=1:k
C.若a、b都能使某种金属发生光电效应,则光电子最大初动能之差Eka﹣Ekb=?b(k﹣1)
D.若a、b是由处于同一激发态的原子跃迁到a态和b态时产生的,则a、b两态能级之差Ea﹣Eb=?b(k﹣1)
15.(2017?海南)如图,空气中有两块材质不同、上下表面平行的透明玻璃板平行放置;一细光束从空气中以某一角度θ(0<θ<90°)入射到第一块玻璃板的上表面。下列说法正确的是( )
A.在第一块玻璃板下表面一定有出射光
B.在第二块玻璃板下表面一定没有出射光
C.第二块玻璃板下表面的出射光方向一定与入射光方向平行
D.第二块玻璃板下表面的出射光一定在入射光延长线的左侧
E.第一块玻璃板下表面的出射光线一定在入射光延长线的右侧
16.(2017?海南)三束单色光1、2和3的波长分别为λ1、λ2和λ3(λ1>λ2>λ3)。分别用这三束光照射同一种金属。已知用光束2照射时,恰能产生光电子。下列说法正确的是( )
A.用光束1照射时,不能产生光电子
B.用光束3照射时,不能产生光电子
C.用光束2照射时,光越强,单位时间内产生的光电子数目越多
D.用光束2照射时,光越强,产生的光电子的最大初动能越大
17.(2017?新课标Ⅲ)在光电效应实验中,分别用频率为va、vb的单色光a、b照射到同种金属上,测得相应的遏止电压分别为Ua和Ub、光电子的最大初动能分别为Eka和Ekb,h为普朗克常量。下列说法正确的是( )
A.若va>vb,则一定有Ua<Ub B.若va>vb,则一定有Eka>Ekb
C.若Ua<Ub,则一定有Eka<Ekb D.若va>vb,则一定有hva﹣Eka>hvb﹣Ekb
18.(2017?浙江)图中给出了“用双缝干涉测量光的波长”实验示意图,双缝S1和S2间距为0.80mm,双缝到屏的距离为0.80m,波长为500nm的单色平行光垂直入射到双缝S1和S2上,在屏上形成干涉条纹,中心轴线OO′上方第1条亮纹中心位置在P1处,第3条亮纹中心位置在P2处,现有1号、2号虫子分别从S1和S2出发以相同速度沿垂直屏方向飞行,1号虫子到达屏后,沿屏直线爬行到P1,2号虫子到达屏后,沿屏直线爬行到P2,假设两条虫子爬行速率均为10﹣3m/s,正确的是( )
A.1号虫子运动路程比2号短
B.两只虫子运动的时间差为0.2s
C.两只虫子运动的时间差为1.0s
D.已知条件不够,两只虫子运动时间差无法计算
三.填空题(共4小题)
19.(2019?江苏)将两支铅笔并排放在一起,中间留一条狭缝,通过这条狭缝去看与其平行的日光灯,能观察到彩色条纹,这是由于光的 (选填“折射”“干涉”或“衍射”)。当缝的宽度 (选填“远大于”或“接近”)光波的波长时,这种现象十分明显。
20.(2018?江苏)光电效应实验中,用波长为λ0的单色光A照射某金属板时,刚好有光电子从金属表面逸出。当波长为的单色光B照射该金属板时,光电子的最大初动能为 ,A、B两种光子的动量之比为 。(已知普朗克常量为h、光速为c)
21.(2018?新课标Ⅰ)如图,△ABC为一玻璃三棱镜的横截面,∠A=30°,一束红光垂直AB边射入,从AC边上的D点射出。其折射角为60°,则玻璃对红光的折射率为 。若改用蓝光沿同一路径入射,则光线在D点射出时的折射角 (填“小于”“等于”或“大于”)60°。
22.(2017?江苏)质子(H)和α粒子(He)被加速到相同动能时,质子的动量 (选填“大于”、“小于”或“等于”)α粒子的动量,质子和α粒子的德布罗意波波长之比为 .
四.实验题(共1小题)
23.(2016?江苏)(1)杨氏干涉实验证明光的确是一种波,一束单色光投射在两条相距很近的狭缝上,两狭缝就成了两个光源,它们发出的光波满足干涉的必要条件,则两列光的 相同.如图所示,在这两列光波相遇的区域中,实线表示波峰,虚线表示波谷,如果放置光屏,在 (选填“A”、“B”或“C”)点会出现暗条纹.
(2)在上述杨氏干涉试验中,若单色光的波长λ=5.89×10﹣7m,双缝间的距离d=1mm,双缝到屏的距离l=2m.求第1个亮光条纹到第11个亮条纹的中心间距.
五.计算题(共13小题)
24.(2019?江苏)在“焊接”视网膜的眼科手术中,所用激光的波长λ=6.4×10﹣7m,每个激光脉冲的能量E=1.5×10﹣2J.求每个脉冲中的光子数目。(已知普朗克常量h=6.63×10﹣34J?s,光速c=3×108m/s,计算结果保留一位有效数字)
25.(2019?江苏)如图所示,某L形透明材料的折射率n=2.现沿AB方向切去一角,AB与水平方向的夹角为θ.为使水平方向的光线射到AB面时不会射入空气,求θ的最大值。
26.(2019?新课标Ⅲ)如图,直角三角形ABC为一棱镜的横截面,∠A=90°,∠B=30°.一束光线平行于底边BC射到AB边上并进入棱镜,然后垂直于AC边射出。
(i)求棱镜的折射率;
(ii)保持AB边上的入射点不变,逐渐减小入射角,直到BC边上恰好有光线射出。求此时AB边上入射角的正弦。
27.(2019?新课标Ⅰ)如图,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3m。距水面4m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin53°=0.8)。已知水的折射率为。
(i)求桅杆到P点的水平距离;
(ⅱ)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍照射在桅杆顶端,求船行驶的距离。
28.(2018?全国)如图,玻璃柱的横截面为半径R=20.0cm的半圆,O点为圆心。光屏CD紧靠在玻璃柱的右侧且与截面底边MN垂直。一光束沿半径方向射向O点,光束和MN的夹角为θ,在光屏CD上出现两个光斑。已知玻璃的折射率为n=。
(1)若θ=60°,求两个光斑间的距离
(2)屏上两个光斑间的距离会随θ大小的变化而改变,求两光斑间的最短距离。
29.(2018?海南)如图,由透明介质构成的半球壳的内外表面半径分别为R和R.一横截面半径为R的平行光束入射到半球壳内表面,入射方向与半球壳的对称轴平行,所有的入射光线都能从半球壳的外表面射出。已知透明介质的折射率为n=.求半球壳外表面上有光线射出区域的圆形边界的半径。不考虑多次反射。
30.(2018?新课标Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°.一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出,EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(i)求出射光相对于D点的入射光的偏角;
(ii)为实现上述光路,棱镜折射率的取值应在什么范围?
31.(2018?新课标Ⅲ)如图,某同学在一张水平放置的白纸上画了一个小标记“?”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点做AC边的垂线交AC于F.该同学在D点正上方向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点做AB边的垂线交直线DF于E;DE=2cm,EF=1cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
32.(2017?江苏)人的眼球可简化为如图所示的模型,折射率相同、半径不同的两个球体共轴,平行光束宽度为D,对称地沿轴线方向射入半径为R的小球,会聚在轴线上的P点.取球体的折射率为,且D=R,求光线的会聚角α.(示意图未按比例画出)
33.(2017?新课标Ⅰ)如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R.已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)。求该玻璃的折射率。
34.(2017?新课标Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示.容器右侧内壁涂有反光材料,其他内壁涂有吸光材料.在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率.
35.(2017?新课标Ⅲ)如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线).已知玻璃的折射率为1.5.现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线).求:
(i)从球面射出的光线对应的入射光线到光轴距离的最大值;
(ii)距光轴的入射光线经球面折射后与光轴的交点到O点的距离.
36.(2016?新课标Ⅰ)如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0m.从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为.
(i)求池内的水深;
(ii)一救生员坐在离池边不远处的高凳上,他的眼睛到地面的高度为2.0m.当他看到正前下方的点光源A时,他的眼睛所接受的光线与竖直方向的夹角恰好为45°.求救生员的眼睛到池边的水平距离(结果保留1位有效数字).
2019年全国各地高考真题分类——光学部分
参考答案与试题解析
一.选择题(共11小题)
C.若入射光子的能量为5.0eV,根据光电效应方程Ek=hv﹣W,可得逸出光电子的最大动能为Ek=5.0eV﹣3.1eV=1.9eV,故C正确;
D.由表格中的数据可知,在产生光电效应的前提下,对同种频率的入射光而言,入射光的强度越大,光电流越大,所以若入射光子的能量为5.0eV,相对光强越强,光电流越大,故D正确。
本题选不正确的,故选:B。
3.【解答】解:干涉条纹在光屏上观察到的图案是间距相等的条纹图象,而衍射条纹中,中间的亮纹的宽度最大,向两边渐渐减小,
因此甲对应单缝,乙对应双缝,故A正确,BCD错误。
故选:A。
4.【解答】解:泊松亮斑是光的衍射现象形成的,而光的衍射现象说明光的波动性;故B正确,ACD错误。
故选:B。
5.【解答】解:A、在双缝中,仍是频率相同的红光,因此能发生干涉现象,故A错误;
B、由于只有红光干涉条纹,因此不会出现彩色条纹,也没有彩色条纹中的红色条纹消失现象,故B错误;
C、在中央条纹,满足光程差为零,则是明条纹,并不变成暗条纹,故C错误;
D、得到白光的干涉条纹后,在光源与单缝之间加上红色滤光片,在双缝中的,由于红光的频率相同,则能发生干涉,但不是彩色条纹,而是明暗相间的红色条纹,故D正确。
故选:D。
6.【解答】解:A、四条谱线Hα、Hβ、Hγ和Hδ,在真空中的波长由长到短,根据,可知,四条谱线Hα、Hβ、Hγ和Hδ,的频率是由低到高;那么它们的能量也是由小到大,
而△E=Em﹣En=hγ,则Hα对应的前后能级之差最小,故A正确;
B、当在同一介质,由于Hδ,能量最大,那么其的折射率也最大,而对Hα的折射率最小,故B错误;
C、在同一介质中,Hδ的折射率最大,由v=,可知,其传播速度最小,故C错误;
D、若用Hγ照射某一金属能发生光电效应,由于Hβ的能量小于Hγ,即Hβ的频率小于Hγ,依据光电效应发生条件,其入射频率不小于极限频率则Hβ不一定能,故D错误;
故选:A。
7.【解答】解:根据光电效应方程:EKm=hγ﹣W0
光速、波长、频率之间关系为:γ=
将数据,代入上式,则有:W0=hγ﹣EKm=6.63×10﹣34J?s×s﹣1﹣1.28×10﹣19J=5.35×10﹣19J
根据逸出功W0=hγ0,得:
γ0==≈8×1014 Hz;
故选:B。
8.【解答】解:A、根据折射率定义公式n=,从空气斜射向玻璃时,入射角相同,光线a对应的折射角较大,故光线a的折射率较小,即na<nb,若增大入射角i,在第二折射面上,则两光的入射角减小,依据光从光密介质进入光疏介质,且入射角大于或等于临界角时,才能发生光的全反射,因此它们不会发生光的全反射,故A错误;
B、根据折射率定义公式n=,从空气斜射向玻璃时,入射角相同,光线a对应的折射角较大,故光线a的折射率较小,即na<nb,则在真空中a光波长大于b光波长,故B错误;
C、只要是横波,均能发生偏振现象,若a光能发生偏振现象,b光一定能发生,故C错误;
D、a光折射率较小,则频率较小,根据E=hγ,则a光光子能量较小,则a光束照射逸出光电子的最大初动能较小,根据qUc=,则a光的遏止电压低,故D正确;
故选:D。
9.【解答】解:光从空气斜射到玻璃,因为玻璃上下表面平行,当第二次折射时折射光线与第一次折射入射光线平行。由于折射率不同,a光偏折较大,b光偏折较小。所以此玻璃对a光的折射率大于对b光的折射率,所以a的频率大于b的频率,给出的各色光中频率大于蓝光的只有紫光,故D正确,ABC错误。
故选:D。
10.【解答】解:能够电离一个分子的能量为E==J=1.98×10﹣18J,故B正确,A、C、D错误。
故选:B。
11.【解答】解:A、干涉要求两波源的频率相同,而强度没有要求,故A错误。
B、由于无线电波以光速传播,根据知,波长不同,频率不同,所以两种无线电波之间不会发生干涉,故B错误。
C、空间中某点加强与减弱取决于到两波源的距离差为半波长的奇、偶数倍。所以两种电波的波峰与波峰叠加最强分布是固定的,而且λ1≠λ2,所以无线电波各自在空间的强弱分布不重合,不过中垂线都是加强点,故C正确,D错误。
故选:C。
二.多选题(共7小题)
12.【解答】解:A、根据光电效应方程得:
Ekm=hγ﹣W0=hγ﹣hγ0
又Ekm=eUC
解得:UC=γ﹣=γ﹣;
当遏止电压为0时,对应的频率为金属的极限频率,结合图可知钠的极限频率小,则钠的逸出功小。故A正确;
B、由UC=γ﹣知U0﹣γ图线的斜率k=,故B正确;
C、由UC=γ﹣知图线的特点与光的强度无关。故C错误;
D、钠的逸出功小,结合Ekm=hγ﹣W0可知,若这两种金属产生的光电子具有相同的最大初动能,则照射到钠的光频率较小。故D错误
故选:AB。
13.【解答】解:A、根据题意可知a光频率低于b光频率,玻璃砖对a光的折射率大于对b光的折射率,b光的折射率较小,以相同角度斜射到同一玻璃板透过平行表面后,b光的折射角较大,所以b光侧移量小,即a光的侧移量大于b光的,故A错误;
B、频率越大,波长越小,通过同一单缝衍射装置时,中央亮条纹宽度越小,故B正确;
C、a光的频率大,故频率之比不可能为,故C错误;
D、频率越大,波长越小,即λa<λb,根据可知pa>pb,故D正确。
故选:BD。
14.【解答】解:A、光子的能量:?=hγ
所以两种光子能量分别为?a和?b,且=k,则:
光子的动量:p=
所以:.故A错误;
B、光子的波长:
双缝干涉装置上相邻亮条纹的间距:
所以:.故B正确;
C、根据光电效应方程可知,光电子的最大初动能:Ekm=hγ﹣W,其中W为金属的逸出功;
则:Eka﹣Ekb=hγa﹣hγb=?b(k﹣1)。故C正确;
D、若a、b是由处于同一激发态的原子跃迁到a态和b态时产生的,设初始激发态的能量为E0,则:?a=hγa=E0﹣Ea
所以:Ea=E0﹣?a
同理:Eb=E0﹣?b
则:Ea﹣Eb=?b﹣?a=﹣?b(k﹣1)。故D错误。
故选:BC。
15.【解答】解:A、光线从第一块玻璃板中的上表面射入,在第一块玻璃板中上表面的折射角和下表面的入射角相等,根据光的可逆原理可知,光在第一块玻璃板下表面一定有出射光,同理,在第二个玻璃板下表面也一定有出射光,故A正确,B错误。
C、因为光在玻璃板中的上表面的折射角和下表面的入射角相等,根据光的可逆原理知,从下表面出射光的折射角和开始在上表面的入射角相等,即两光线平行,所以第二块玻璃板下表面的出射光方向一定与入射光方向平行,故C正确。
D、根据光线在玻璃板中发生偏折,由于折射角小于入射角,可知第二块玻璃板下表面的出射光一定在入射光延长线的左侧,故D正确,E错误。
故选:ACD。
16.【解答】解:AB、依据波长与频率的关系:,因λ1>λ2>λ3,那么γ1<γ2<γ3;由于用光束2照射时,恰能产生光电子,因此用光束1照射时,不能产生光电子,而光束3照射时,一定能产生光电子,故A正确,B错误;
CD、用光束2照射时,光越强,单位时间内产生的光电子数目越多,而由光电效应方程:Ekm=hγ﹣W,可知,光电子的最大初动能与光的强弱无关,故C正确,D错误;
故选:AC。
17.【解答】解:AB、根据光电效应方程Ekm=hv﹣W0知,va>vb,逸出功相同,则Eka>Ekb,又Ekm=eUc,则Ua>Ub,故A错误,B正确。
C、根据Ekm=eUc知,若Ua<Ub,则一定有Eka<Ekb,故C正确。
D、逸出功W0=hv﹣Ekm,由于金属的逸出功相同,则有:hva﹣Eka=hvb﹣Ekb,故D错误。
故选:BC。
18.【解答】解:A、由题,结合干涉条纹的宽度公式:可知,该光的干涉条纹的宽度:x=m
第1条亮纹中心位置在P1处,所以:m
第3条亮纹中心位置在P2处,所以:m
所以1号虫子的路程为:;
2号虫子的路程为:,
则:=1.5×10﹣3﹣5×10﹣4﹣0.80×10﹣3=0.2×10﹣3m.故A正确;
BCD、两只虫子运动的时间差s.故B正确,CD错误
故选:AB。
三.填空题(共4小题)
19.【解答】解:将两支铅笔并排放在一起,中间留一条狭缝,通过这条狭缝去看与其平行的日光灯,能观察到彩色条纹,这是由于光的衍射产生的。
当缝的宽度与光波波长接近时,衍射现象非常明显。
故答案为:衍射,接近。
20.【解答】解:由题知,金属板的逸出功为为:
W0=hγ0=
当波长为的单色光B照射该金属板时,根据爱因斯坦光电效应方程得:
Ek=h﹣W0=
根据p=得A、B两种光子的动量之比为:
pA:pB=:λ0=1:2
故答案为:,1:2。
21.【解答】解:由下图可知,当红光进入玻璃三棱镜后,在AB界面上垂直进入,到达AC界面发生了折射现象,根据几何关系可得:入射角的大小为∠1=30°,又因为已知折射角的大小为γ=60°,
利用折射定律可解得:玻璃对红光的折射率。
若改用蓝光沿同一路径入射,在AB界面上仍是垂直进入,由几何关系可知,其入射角不变;当到达AC界面发生折射现象,由于蓝光的折射率比红光的折射率大,再利用折射定律,
在∠1=30°不变的情况下,由于折射率增加,可得出其折射角将增加,即:光线在D点射出时的折射角大于60°。
故答案为:;大于。
22.【解答】解:动能与动量的关系为:P=,
物质波的波长:λ=,
联立得到:∝,
质子(H)和α粒子(He)质量之比为1:4,故物质波的波长之比为2:1;
故答案为:小于,2:1.
四.实验题(共1小题)
23.【解答】解:(1)产生稳定干涉图样的必要条件是两束光的频率相同.A、B两点是波峰与波峰、波谷与波谷相遇的点,是振动加强点,出现明条纹,C点波峰与波谷相遇,振动减弱,出现暗条纹.
(2)相邻干涉条纹的间距为△x==×5.89×10﹣7m=1.178×10﹣3m
则第1个亮光条纹到第11个亮条纹的中心间距为 S=10△x=1.178×10﹣2m
故答案为:(1)频率,C.(2)第1个亮光条纹到第11个亮条纹的中心间距为1.178×10﹣2m.
五.计算题(共13小题)
24.【解答】解:光子的能量为:?==J=3.1×10﹣19J。
每个脉冲中的光子数目为:n=≈5×1016个
答:每个脉冲中的光子数目为5×1016个
25.【解答】解:当光线在AB面上刚好发生全反射时θ最大,设全反射临界角为C,则sinC==
可得 C=30°
根据几何关系有 C+θ=90°
可得 θ=60°
答:θ的最大值是60°。
26.【解答】解:(i)光路图及相关量如图所示。
光束在AB边上折射,由折射定律得:
①
式中n是棱镜的折射率。由几何关系可知:α+β=60° ②
由几何关系和反射定律得:β=β′=∠B ③
联立①②③式,并代入i=60°得:n=④
(ii)设改变后的入射角为i′,折射角为α′,由折射定律得:⑤
依题意,光束在BC边上的入射角为全反射的临界角θc,且:sinθc=⑥
由几何关系得:θc═α'+30° ⑦
由④⑤⑥⑦式得入射角的正弦为:sini′=⑧
答:(i)棱镜的折射率为;
(ii)AB边上入射角的正弦为。
27.【解答】解:(i)设光束从水面射出的点到桅杆的水平距离为x1,到P点的水平距离为x2.桅杆的高度为h1,P点处水深为h2.激光束在水中与竖直方向的夹角为θ。
由几何关系有:
=tan53°…①
=tanθ…②
由折射定律有:n=…③
设桅杆到P点的水平距离为x,则:x=x1+x2…④
联立①②③④并代入数据解得:x=7m…⑤
(ii)设激光束在水中与竖直方向的夹角为45°时,从水面出射的方向与竖直方向的夹角为i′。
由折射定律有:n=…⑥
设船向左行驶的距离为x′,此时光束从水面射出的点到桅杆的水平距离为x1′,到P点的水平距离为x2′,则
x1′+x2′=x′+x…⑦
=tani′…⑧
=tan45°…⑨
联立⑤⑥⑦⑧⑨并代入数据解得:x′=(6﹣3)m≈5.5m
答:
(i)桅杆到P点的水平距离是7m;
(ⅱ)船行驶的距离是5.5m。
28.【解答】解:(1)光束在MN界面上一部分反射,设反射光与光屏CD的交点为C,另一部分折射,设折射光与光屏的交点为D,入射角为r,折射角为i,光路图如图所示,由几何关系得:r=90°﹣θ=30°
得:LCN==R
根据折射定律得 n=
可得,i=60°
则LDN==R
所以两个光斑间的距离 LCD=LCN+LDN=R=cm
(2)屏上两个光斑间的距离会随θ的减小而变短,当光线在MN就要发生全反射时,两光斑间距离最短,由临界角公式sinC=得:
sinC=
tanC===
所以两光斑间的最短距离 Lmin=
联立解得 Lmin=20cm
答:
(1)若θ=60°,两个光斑间的距离是cm。
(2)屏上两个光斑间的距离会随θ大小的变化而改变,两光斑间的最短距离是20cm。
29.【解答】解:设光从半球壳内表面边沿上的A点入射,入射角为90°(全反射临界角也为α),然后在半球壳外表面内侧的B点发生折射,入射角为β,如图所示。
由全反射临界角的定义得 1=nsinα①
由正弦定理得
=②
OD为对称思,设∠BOD=γ,由几何关系可知
γ=﹣(α﹣β)③
设B点到OD的距离为r,即为所求的半球壳外表面上有光线射出区域的圆形边界的半径,由几何关系有
r=Rsinγ④
由①②③④及题给数据解得 r=R
答:半球壳外表面上有光线射出区域的圆形边界的半径为R。
30.【解答】解:(i)由于D是CG的中点,GE⊥AC,根据几何关系可得:光束在D点发生折射时的折射角为γD=30°;
那么,根据几何关系可得:在E点的入射角、反射角均为γD+30°=60°;在F点的入射角为αF=30°;
那么,设入射角为αD,可得:折射角γF=αD,故出射光相对于D点的入射光的偏角为60°﹣αD+γF=60°;
(ii)由E点反射角为60°可得:EF∥BC;
故根据D点折射角为γD=30°,在F点的入射角为αF=30°可得:棱镜折射率;
根据光束在E点入射角为60°,发生全反射可得:,故棱镜折射率的取值范围为;
答:(i)出射光相对于D点的入射光的偏角为60°;
(ii)为实现上述光路,棱镜折射率的取值范围为。
31.【解答】解:连接DO,点E是三角形AOD的垂心,DE=2cm,EF=1cm,说明三角形OAD是等边三角形,点E也是重心、中心,故画出光路图,如图所示:
故入射角为60°,折射角为30°,故折射率为:
n==;
答:三检镜的折射率为。
32.【解答】解:设入射角为i.由几何关系得:sini==,
解得:i=45°
由折射定律有:n=,
解得折射角为:r=30°
且由几何关系有:i=r+,
解得:α=30°
答:光线的会聚角α是30°.
33.【解答】解:由题意,结合光路的对称性与光路可逆可知,与入射光相对于OC轴对称的出射光线一定与入射光线平行,所以从半球面射入的光线经折射后,将在圆柱体底面中心C点反射,如图:
设光线在半球处的入射角为i,折射光线的折射角为r,则:
sini=nsinr…①
由正弦定理得:=…②
由几何关系可知,入射点的法线与OC之间的夹角也等于i,该光线与OC之间的距离:L=0.6R
则:sini=…③
由②③得:sinr=
由①③④得:n=≈1.43
答:该玻璃的折射率为1.43。
34.【解答】解:设从光源发出的光直接射到D点的光线的入射角为i1,折射角为γ1,在剖面内做光源相对于镜面的对称点C,连接CD,交镜面与E点,由光源射向E点的光线反射后由ED射向D点,设入射角为i2,折射角为γ2,如图;
设液体的折射率为n,由折射定律:
nsini1=sinγ1
nsini2=sinγ2
由题意:γ1+γ2=90°
联立得:
由图中几何关系可得:;
联立得:n=1.55
答:该液体的折射率为1.55.
35.【解答】解:(i)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l.
i=ic
设n是玻璃的折射率,由全反射临界角的定义有
nsinic=l
由几何关系有
sini=
联立可得:l=R
(ii)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有
nsini1=sinr1
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有
由几何关系有
∠C=r1﹣i1
sini1=
联立可得:OC=R≈2.74R.
答:(i)从球面射出的光线对应的入射光线到光轴距离的最大值为;
(ii)距光轴的入射光线经球面折射后与光轴的交点到O点的距离2.74R.
36.【解答】解:(i)光由A射向B点发生全反射,光路如图所示.
图中入射角θ等于临界角C,则有
sinθ==
由题,=3m,由几何关系可得:
=4m
同课章节目录
