人教A版数学必修5 3.3.2 简单的线性规划问题(共21张ppt)
文档属性
| 名称 | 人教A版数学必修5 3.3.2 简单的线性规划问题(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 646.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-12 23:08:51 | ||
图片预览







文档简介
课件21张PPT。3.3.2 简单的线性规划问题(第二课时) 1.体会线性规划的基本思想,并能借助几何直观解决一些简单的实际问题;
2.利用线性规划解决具有限制条件的不等式;
3.培养学生搜集、整理和分析信息的能力,提高学生数学建模和解决实际问题的能力.重点:用线性规划解决现实生活中的问题.难点:把实际问题转化为线性规划问题和寻找整数解.重 难 点:学习目标:求z=28x+21y的最小值,使 x,y满足:
复习回顾解方程组得M的坐标为所以zmin=28x+21y=16.在实际问题中常遇到两类问题:
一是在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务; 二是给定一项任务,如何合理地安排和规划能以最少的人力、物力、资金等资源来完成它.下面我们来看看线性规划在实际中的一些应用.新课导入例1 营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪.1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg脂肪,花费28元;而1 kg食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B各多少kg?(用量最省问题)
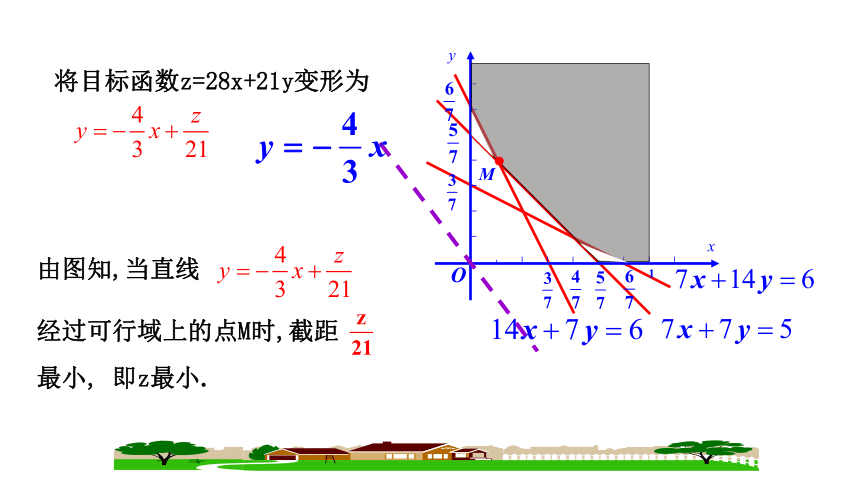
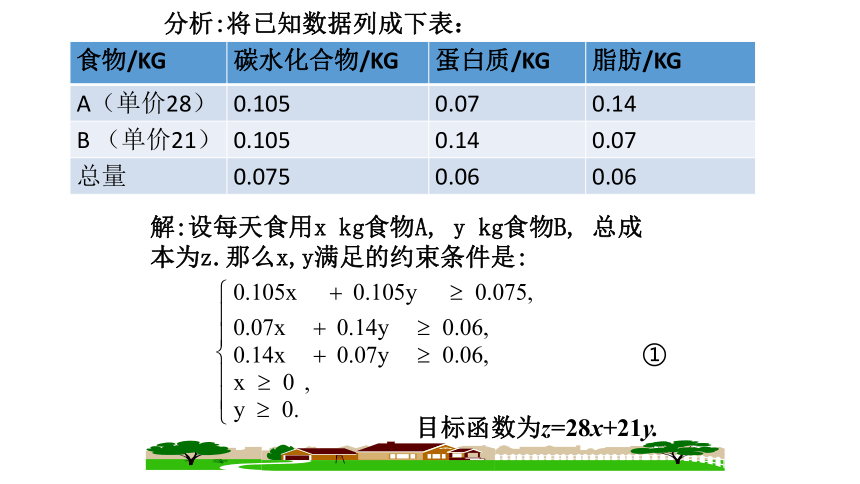
探究一 简单线性规划问题在实际问题中的应用课堂探究分析:将已知数据列成下表:①解:设每天食用x kg食物A, y kg食物B, 总成本为z.那么x,y满足的约束条件是:目标函数为z=28x+21y.即复习巩固。②二元一次不等式组①等价于注意:
答:每天食用食物A约143 g,食物B约571 g,能够满足日常饮食要求,又使花费最低,最低成本为16元.探究二 关于整点最优解的问题例2 要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 : 解:设需截第一种钢板x张,第二种钢板y张,钢板总张数为z,则 作出可行域(如图)目标函数为 z=x+y今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。X张y张2x+y=15x+3y=27x+2y=18x+y =0直线z=x+y经过的最小整点是B(3,9)和D(4,8),它们是最优解. 作出初始直线L0:x+y=0,目标函数z= x+y当直线经过点A时z取得最小值z=x+y=11.4,x+y=12代入约束条件解得点B,C的坐标B(3,9)和C(4.5,7.5)调整优值法246181282724681015但它不是最优整数解.取z=x+y=12答(略)C(4.5,7.5)D(4,8)2x+y=15x+3y=27x+2y=18x+y =0经过可行域内的整点B(3,9)和C(4,8)时,z=x+y=12是最优解.答:(略)作出一组平行直线z = x+y,目标函数z = x+y网格法在可行域内打出网格线,当直线经过点A时z=x+y=11.4,但它不是最优整数解,将直线x+y=11.4继续向上平移,1212182715978 A、B 两个居民小区的居委会组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动,两个小区都有同学参加.已知A区的每位同学往返车费是3元,每人可为5位老人服务;B区的每位同学往返车费是5元,每人可为3位老人服务.如果要求B 区参与活动的同学比A 区的同学多,且去敬老院的往返总车费不超过37元.怎样安排参与活动同学的人数,才能使受到服务的老人最多?受到服务的老人最多是多少人?课堂检测??Oy=x3x+5y=37x=1xy1 2 3 4 5 68
7
6
5
4
3
2
15x+3y=0(1)审题:仔细阅读材料,抓住关键,准确理解题意,明确有哪些限制条件,借助表格或图形理清变量之间的关系.
(2)设元:设问题中起关键作用的(或关联较多的)量为未知量x,y,并列出相应的不等式组和目标函数.
(3)作图:准确作出可行域,平移找点(最优解).
(4)求解:代入目标函数求解(最大值或最小值).
(5)作答:根据结果,检验反馈.
课堂小结利用线性规划解决实际问题的一般步骤:
在可行域内找出整点最优解的一般方法:1.若区域“顶点”处恰好为整点,那么它就是最优解;(在包括边界的情况下)
2.调整优值法:若区域“顶点”不是整点或不包括边界时,应先求出该点坐标,并计算目标函数值Z,然后在可行域内适当放缩目标函数值,使它为整数,且与Z最接近,在这条对应的直线中,取可行域内整点,如果没有整点,继续放缩,直至取到整点为止。
3.网格法:即打网格、平移直线、找出整数最优解。
(网格法一般用于数不大的问题中且要求作图必须精准)
1、某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元,2000元。甲、乙产品都需要在A,B两种设备上加工,在每台A,B设备上加工1件甲产品所需工时分别为1h、2h,加工1件乙产品所需工时分别为2h、1h,A,B两种设备每月有效使用台时数分别为400h和500h。如何安排生产可使收入最大?课后巩固
2、 一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4 t、硝酸盐18 t;生产1车皮乙种肥料需要的主要原料是磷酸盐1 t、硝酸盐15 t.现在库存磷酸盐10 t、硝酸盐66 t,在此基础上生产这两种混合肥料.列出满足生产条件的数学关系式,并画出相应的平面区域.若生产1车皮甲种肥料,产生的利润为10 000元;生产1车皮乙种肥料,产生的利润为5 000元.那么分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?(效益最佳问题)3.某运输公司接受了向抗洪抢险地区每天至少运送180吨支援物资的任务,该公司有8辆载重量为6吨的A型卡车和4辆载重量为10吨的B型卡车,有10名驾驶员;每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的成本费A型卡车为320元,B型卡车为504元,问如何安排车辆才能使该公司所花的成本费最低,最低为多少元?(要求每型卡车至少安排一辆)
2.利用线性规划解决具有限制条件的不等式;
3.培养学生搜集、整理和分析信息的能力,提高学生数学建模和解决实际问题的能力.重点:用线性规划解决现实生活中的问题.难点:把实际问题转化为线性规划问题和寻找整数解.重 难 点:学习目标:求z=28x+21y的最小值,使 x,y满足:
复习回顾解方程组得M的坐标为所以zmin=28x+21y=16.在实际问题中常遇到两类问题:
一是在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务; 二是给定一项任务,如何合理地安排和规划能以最少的人力、物力、资金等资源来完成它.下面我们来看看线性规划在实际中的一些应用.新课导入例1 营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪.1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg脂肪,花费28元;而1 kg食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B各多少kg?(用量最省问题)
探究一 简单线性规划问题在实际问题中的应用课堂探究分析:将已知数据列成下表:①解:设每天食用x kg食物A, y kg食物B, 总成本为z.那么x,y满足的约束条件是:目标函数为z=28x+21y.即复习巩固。②二元一次不等式组①等价于注意:
答:每天食用食物A约143 g,食物B约571 g,能够满足日常饮食要求,又使花费最低,最低成本为16元.探究二 关于整点最优解的问题例2 要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 : 解:设需截第一种钢板x张,第二种钢板y张,钢板总张数为z,则 作出可行域(如图)目标函数为 z=x+y今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。X张y张2x+y=15x+3y=27x+2y=18x+y =0直线z=x+y经过的最小整点是B(3,9)和D(4,8),它们是最优解. 作出初始直线L0:x+y=0,目标函数z= x+y当直线经过点A时z取得最小值z=x+y=11.4,x+y=12代入约束条件解得点B,C的坐标B(3,9)和C(4.5,7.5)调整优值法246181282724681015但它不是最优整数解.取z=x+y=12答(略)C(4.5,7.5)D(4,8)2x+y=15x+3y=27x+2y=18x+y =0经过可行域内的整点B(3,9)和C(4,8)时,z=x+y=12是最优解.答:(略)作出一组平行直线z = x+y,目标函数z = x+y网格法在可行域内打出网格线,当直线经过点A时z=x+y=11.4,但它不是最优整数解,将直线x+y=11.4继续向上平移,1212182715978 A、B 两个居民小区的居委会组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动,两个小区都有同学参加.已知A区的每位同学往返车费是3元,每人可为5位老人服务;B区的每位同学往返车费是5元,每人可为3位老人服务.如果要求B 区参与活动的同学比A 区的同学多,且去敬老院的往返总车费不超过37元.怎样安排参与活动同学的人数,才能使受到服务的老人最多?受到服务的老人最多是多少人?课堂检测??Oy=x3x+5y=37x=1xy1 2 3 4 5 68
7
6
5
4
3
2
15x+3y=0(1)审题:仔细阅读材料,抓住关键,准确理解题意,明确有哪些限制条件,借助表格或图形理清变量之间的关系.
(2)设元:设问题中起关键作用的(或关联较多的)量为未知量x,y,并列出相应的不等式组和目标函数.
(3)作图:准确作出可行域,平移找点(最优解).
(4)求解:代入目标函数求解(最大值或最小值).
(5)作答:根据结果,检验反馈.
课堂小结利用线性规划解决实际问题的一般步骤:
在可行域内找出整点最优解的一般方法:1.若区域“顶点”处恰好为整点,那么它就是最优解;(在包括边界的情况下)
2.调整优值法:若区域“顶点”不是整点或不包括边界时,应先求出该点坐标,并计算目标函数值Z,然后在可行域内适当放缩目标函数值,使它为整数,且与Z最接近,在这条对应的直线中,取可行域内整点,如果没有整点,继续放缩,直至取到整点为止。
3.网格法:即打网格、平移直线、找出整数最优解。
(网格法一般用于数不大的问题中且要求作图必须精准)
1、某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元,2000元。甲、乙产品都需要在A,B两种设备上加工,在每台A,B设备上加工1件甲产品所需工时分别为1h、2h,加工1件乙产品所需工时分别为2h、1h,A,B两种设备每月有效使用台时数分别为400h和500h。如何安排生产可使收入最大?课后巩固
2、 一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4 t、硝酸盐18 t;生产1车皮乙种肥料需要的主要原料是磷酸盐1 t、硝酸盐15 t.现在库存磷酸盐10 t、硝酸盐66 t,在此基础上生产这两种混合肥料.列出满足生产条件的数学关系式,并画出相应的平面区域.若生产1车皮甲种肥料,产生的利润为10 000元;生产1车皮乙种肥料,产生的利润为5 000元.那么分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?(效益最佳问题)3.某运输公司接受了向抗洪抢险地区每天至少运送180吨支援物资的任务,该公司有8辆载重量为6吨的A型卡车和4辆载重量为10吨的B型卡车,有10名驾驶员;每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的成本费A型卡车为320元,B型卡车为504元,问如何安排车辆才能使该公司所花的成本费最低,最低为多少元?(要求每型卡车至少安排一辆)
