人教A版数学必修5 3.3.2 简单的线性规划(共17张ppt)
文档属性
| 名称 | 人教A版数学必修5 3.3.2 简单的线性规划(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 722.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-12 23:08:06 | ||
图片预览






文档简介
课件17张PPT。
3.3.2 简单的线性规划第二课时学习目标:
1.巩固简单的线性规划的最值问题,掌握解决简单的线性规划问题的基本思路和主要方法;
2. 能解决简单的含参问题,进一步加深对线性规划知识的理解;
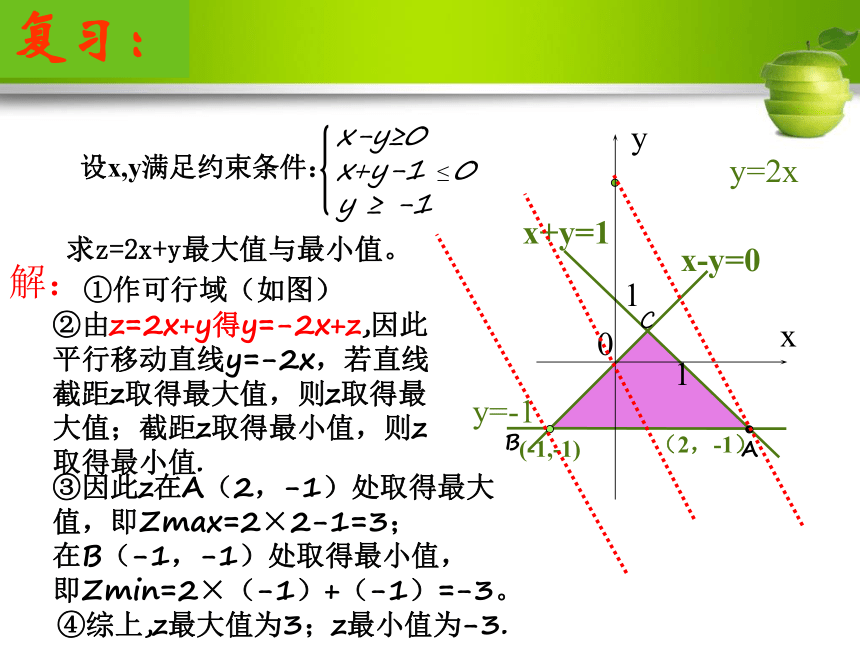
3. 体会线性规划的基本思想:数形结合思想二元一次最大值最小值线性约束条件可行解 最大值 最小值 复习:解线性规划问题的步骤: (2)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域;复习: 求z=2x+y最大值与最小值。
设x,y满足约束条件:①作可行域(如图)③因此z在A(2,-1)处取得最大值,即Zmax=2×2-1=3;
在B(-1,-1)处取得最小值,
即Zmin=2×(-1)+(-1)=-3。②由z=2x+y得y=-2x+z,因此平行移动直线y=-2x,若直线截距z取得最大值,则z取得最大值;截距z取得最小值,则z取得最小值.④综上,z最大值为3;z最小值为-3.解:y=2x复习:非线性目标函数的最值的求解策略
(1)z=(x-a)2+(y-b)2型的目标函数可转化为点(x,y)与点(a,b)距离的平方;特别地,z=x2+y2型的目标函数表示可行域内的点到原点的距离的平方.(2)z= 型的目标函数可转化为点(x,y)与点(a,b)
连线的斜率.
(2)z= 型的目标函数可转化为点(x,y)与点(a,b)
连线的斜率.
4x-3y-12=0x+2y-3=0X-2y+7=0P(-3,-1)x+2y-3=0X-2y+7=04x-3y-12=0P(-3,-1)Q(x,y)题型一:约束条件含参问题2xoy5DCx-y+5=0x=2-5y=ay=ay=ay=5y=77答案:5≤a<7变式训练0 若z=ax+y的最大值为4,则a= ( )
A. 3 B. 2 C. -2 D. -3题型二:目标函数含参数z=ax+y得y=-ax+z , z最大值为4. 画出可行域如图,解得A(2,0),B(1,1).若过点A(2,0)时取最大值4,则a=2,验证符合条件;若过点B(1,1)时取最大值4,则a=3,而若a=3,则z=3x+y最大值为6(此时A(2,0)是最大值点),不符合题意.选B.活学活用:活学活用:【总结】含参数的线性目标函数问题的求解策略
(1)约束条件中含有参数:此时可行域是可变的,应分情况作出可行域,结合条件求出不同情况下的参数值.(2)目标函数中含有参数:此时目标函数对应的直线是可变的,如果斜率一定,则对直线作平移变换;如果斜率可变,则要利用斜率与倾斜角间的大小关系分情况确定最优解的位置,从而求出参数的值.
3.3.2 简单的线性规划第二课时学习目标:
1.巩固简单的线性规划的最值问题,掌握解决简单的线性规划问题的基本思路和主要方法;
2. 能解决简单的含参问题,进一步加深对线性规划知识的理解;
3. 体会线性规划的基本思想:数形结合思想二元一次最大值最小值线性约束条件可行解 最大值 最小值 复习:解线性规划问题的步骤: (2)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域;复习: 求z=2x+y最大值与最小值。
设x,y满足约束条件:①作可行域(如图)③因此z在A(2,-1)处取得最大值,即Zmax=2×2-1=3;
在B(-1,-1)处取得最小值,
即Zmin=2×(-1)+(-1)=-3。②由z=2x+y得y=-2x+z,因此平行移动直线y=-2x,若直线截距z取得最大值,则z取得最大值;截距z取得最小值,则z取得最小值.④综上,z最大值为3;z最小值为-3.解:y=2x复习:非线性目标函数的最值的求解策略
(1)z=(x-a)2+(y-b)2型的目标函数可转化为点(x,y)与点(a,b)距离的平方;特别地,z=x2+y2型的目标函数表示可行域内的点到原点的距离的平方.(2)z= 型的目标函数可转化为点(x,y)与点(a,b)
连线的斜率.
(2)z= 型的目标函数可转化为点(x,y)与点(a,b)
连线的斜率.
4x-3y-12=0x+2y-3=0X-2y+7=0P(-3,-1)x+2y-3=0X-2y+7=04x-3y-12=0P(-3,-1)Q(x,y)题型一:约束条件含参问题2xoy5DCx-y+5=0x=2-5y=ay=ay=ay=5y=77答案:5≤a<7变式训练0
A. 3 B. 2 C. -2 D. -3题型二:目标函数含参数z=ax+y得y=-ax+z , z最大值为4. 画出可行域如图,解得A(2,0),B(1,1).若过点A(2,0)时取最大值4,则a=2,验证符合条件;若过点B(1,1)时取最大值4,则a=3,而若a=3,则z=3x+y最大值为6(此时A(2,0)是最大值点),不符合题意.选B.活学活用:活学活用:【总结】含参数的线性目标函数问题的求解策略
(1)约束条件中含有参数:此时可行域是可变的,应分情况作出可行域,结合条件求出不同情况下的参数值.(2)目标函数中含有参数:此时目标函数对应的直线是可变的,如果斜率一定,则对直线作平移变换;如果斜率可变,则要利用斜率与倾斜角间的大小关系分情况确定最优解的位置,从而求出参数的值.
