人教A版数学必修5 2.5.1 等比数列的前n项和(共27张ppt)
文档属性
| 名称 | 人教A版数学必修5 2.5.1 等比数列的前n项和(共27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-12 23:03:35 | ||
图片预览






文档简介
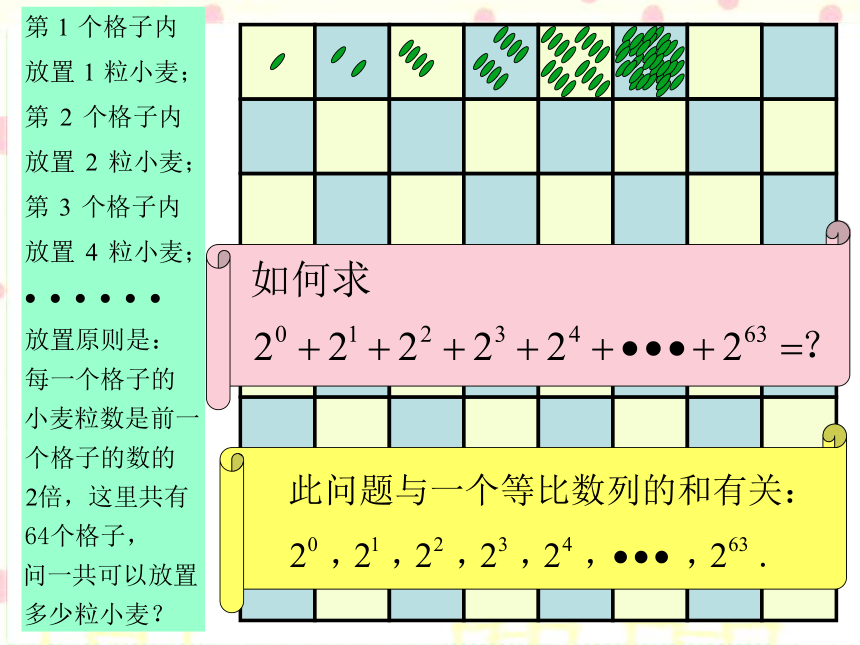
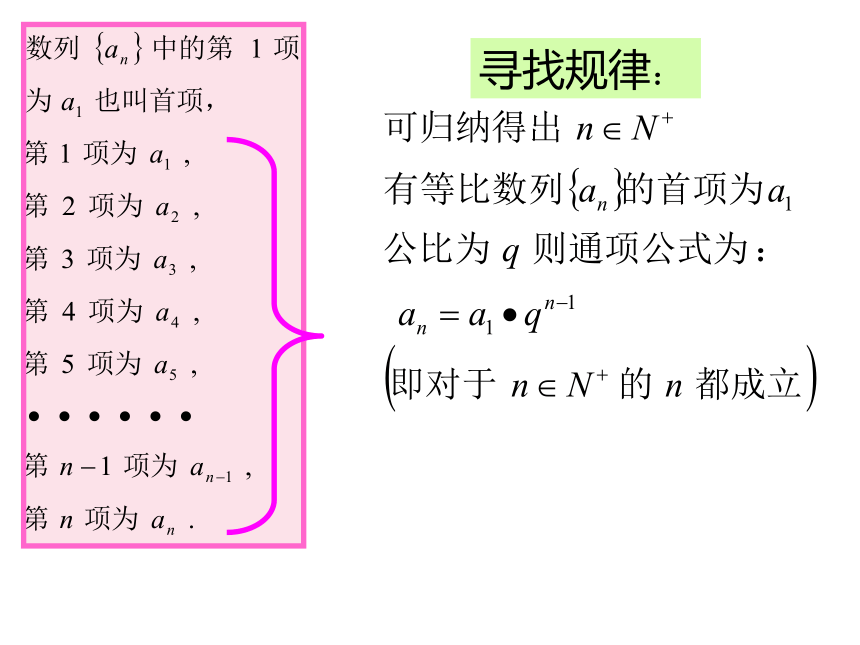
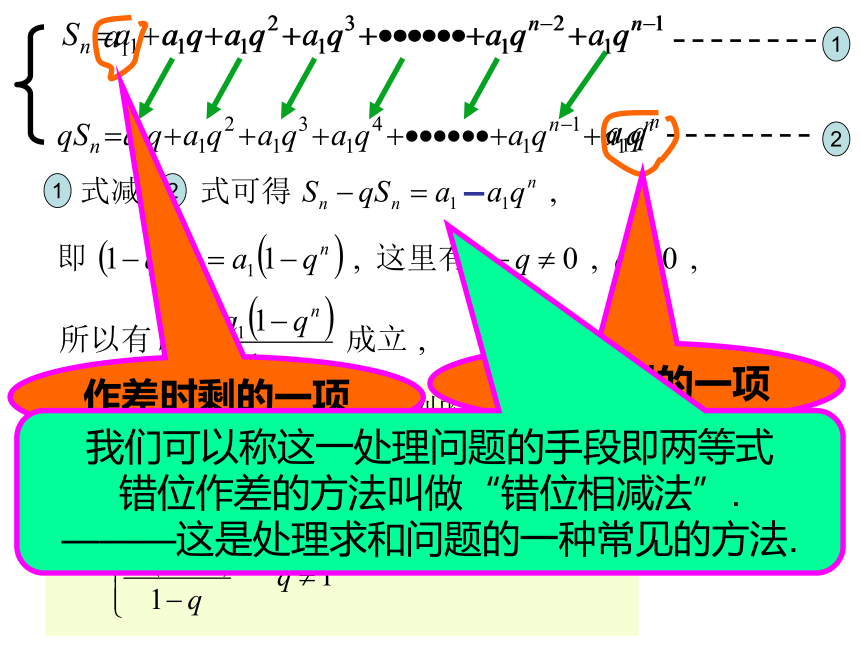
课件27张PPT。 国际象棋起源于古代印度,相传国王要奖赏国际象棋的发明者,问他想要什么,发明者说:“请在棋盘的第一个格子上放上1颗麦粒,第二个格子里放上2颗麦粒,第三个格子里放上4颗麦粒,以此类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的两倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”国王觉得这个要求不高,就欣然同意了.假定千粒麦子的质量为40克,据查目前世界全年小麦产量约6亿吨,根据以上数据,判断国王是否能实现他的诺言.知识引言下面我们学习的内容是寻找规律: 渐入佳境 知识殿堂1212作差时剩的一项作差时剩的一项我们可以称这一处理问题的手段即两等式
错位作差的方法叫做“错位相减法”.
———这是处理求和问题的一种常见的方法.百花齐放 等比数列的前n项和公式可不只有上面这种方法啊!它的推导方法还有好多种,有兴趣的同学可别忘了下去研究啊!
当公比q不确定时,应当分q=1和q≠1两种情况讨论。不要顾此失彼据查目前世界全年小麦产量约6亿吨,根据以上数据,判断国王是否能实现他的诺言?又获丰收【公式的应用】还可以:【公式的应用】小试牛刀1100 5 31313再试牛刀 通过上面例题与习题的求解,可以看出,在公式中涉及到了五个量,我们只要知道其中的三个量,利用等比数列的通项公式,及等比数列的前n项和公式就可以求出另外两个量。即“知三求二”。 例2、已知等比数列 ;(1)再展才华 例3.某商场今年销售计算机 5000台,如果平均每年的销售量
比上一年增加10%,那么从今年
起,大约几年内可使总销售量到
30000台 (保留到个位)?【公式的实际应用】学以致用答:约5年内可以使总销售量达到30000台.解:练习:远望巍巍塔七层, 分析:这首古诗前三句给大家展现了一幅美丽的夜景,最后一句把它变成了一个数学问题?你能用今天的知识求出这首古诗的答案吗? 红光点点倍加增,其灯三百八十一,请问尖头几盏灯?这首古诗的答案是什么??古题今解巩固练习:
1.根据下列各题中的条件,求相应的等比数列 的前n项和Sn
(1)a1=3,q=2,n=6
(2)a1=2,q=3,an=162
2.数列a,a2,a3,…,an的前n项和为( )
A. B. 0 C. n D. 或0 或n
答案:(1)S6=189 (2)Sn=242D登峰造极对于有兴趣的同学们一定不要忘了,探讨一下等比数列的前n项和还有没有其他的推导方法。另劈蹊径等比数列前n项和公式的其他推导方法(一) 用等比定理推导当 q = 1 时 Sn = n a1或Sn = a1 + a2 + a3 + …….+ an-1 + an = a1 + a1q + a1q2 +…..+ a1qn-2 + a1qn-1= a1+ q ( a1 + a1q + ….+ a1qn-3 + a1qn-2 )= a1 + q Sn-1 = a1 + q ( Sn – an )四、小结:1、两个公式:2、数学方法:3、两种思想:五、 作业:教材A组p61 、 1、2、3.错位相减法。分类讨论的思想(q=1和q≠1)
方程思想(知三求二)皆大欢喜
错位作差的方法叫做“错位相减法”.
———这是处理求和问题的一种常见的方法.百花齐放 等比数列的前n项和公式可不只有上面这种方法啊!它的推导方法还有好多种,有兴趣的同学可别忘了下去研究啊!
当公比q不确定时,应当分q=1和q≠1两种情况讨论。不要顾此失彼据查目前世界全年小麦产量约6亿吨,根据以上数据,判断国王是否能实现他的诺言?又获丰收【公式的应用】还可以:【公式的应用】小试牛刀1100 5 31313再试牛刀 通过上面例题与习题的求解,可以看出,在公式中涉及到了五个量,我们只要知道其中的三个量,利用等比数列的通项公式,及等比数列的前n项和公式就可以求出另外两个量。即“知三求二”。 例2、已知等比数列 ;(1)再展才华 例3.某商场今年销售计算机 5000台,如果平均每年的销售量
比上一年增加10%,那么从今年
起,大约几年内可使总销售量到
30000台 (保留到个位)?【公式的实际应用】学以致用答:约5年内可以使总销售量达到30000台.解:练习:远望巍巍塔七层, 分析:这首古诗前三句给大家展现了一幅美丽的夜景,最后一句把它变成了一个数学问题?你能用今天的知识求出这首古诗的答案吗? 红光点点倍加增,其灯三百八十一,请问尖头几盏灯?这首古诗的答案是什么??古题今解巩固练习:
1.根据下列各题中的条件,求相应的等比数列 的前n项和Sn
(1)a1=3,q=2,n=6
(2)a1=2,q=3,an=162
2.数列a,a2,a3,…,an的前n项和为( )
A. B. 0 C. n D. 或0 或n
答案:(1)S6=189 (2)Sn=242D登峰造极对于有兴趣的同学们一定不要忘了,探讨一下等比数列的前n项和还有没有其他的推导方法。另劈蹊径等比数列前n项和公式的其他推导方法(一) 用等比定理推导当 q = 1 时 Sn = n a1或Sn = a1 + a2 + a3 + …….+ an-1 + an = a1 + a1q + a1q2 +…..+ a1qn-2 + a1qn-1= a1+ q ( a1 + a1q + ….+ a1qn-3 + a1qn-2 )= a1 + q Sn-1 = a1 + q ( Sn – an )四、小结:1、两个公式:2、数学方法:3、两种思想:五、 作业:教材A组p61 、 1、2、3.错位相减法。分类讨论的思想(q=1和q≠1)
方程思想(知三求二)皆大欢喜
