11.2.1 三角形的内角学案(要点讲解+当堂检测+答案)
文档属性
| 名称 | 11.2.1 三角形的内角学案(要点讲解+当堂检测+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-13 00:00:00 | ||
图片预览

文档简介
人教版数学八年级上册同步学案
第十一章 三角形
11.2 与三角形有关的角
11.2.1 三角形的内角
要 点 讲 解
要点一 三角形的内角和定理
1. 三角形三个内角的和等于180°.
2. 定理的推理证明:
如图,过点B作BD∥AC.根据两直线平行,内错角相等,可得∠1=∠A.
又根据两直线平行,同旁内角互补,可得∠1+∠ABC+∠C=180°,所以∠A+∠ABC+∠C=180°.
在探究三角形内角和定理时,采用了转化的数学思想.
经典例题1 已知,在△ABC中,∠B=3∠A,∠C=5∠A.求∠A,∠B,∠C的度数.
解析:根据三角形内角和定理及已知条件求出∠A的度数,即可得出∠B,∠C的度数.
解:根据三角形内角和定理及已知条件,得∠A+3∠A+5∠A=180°.
所以∠A=20°,所以∠B=60°,∠C=100°.
要点二 直角三角形的性质与判定
性质:直角三角形的两个锐角互余.
判定:
1. 三角形有一个角是直角;
2. 有两个角互余的三角形是直角三角形.
在三角形中,两个锐角互余的前提条件必须是在直角三角形中,若△ABC是直角三角形(∠C为直角),则∠A+∠B=90°;反之,若在△ABC中,∠A+∠B=90°,则△ABC为直角三角形,直角三角形ABC也可以写成Rt△ABC.
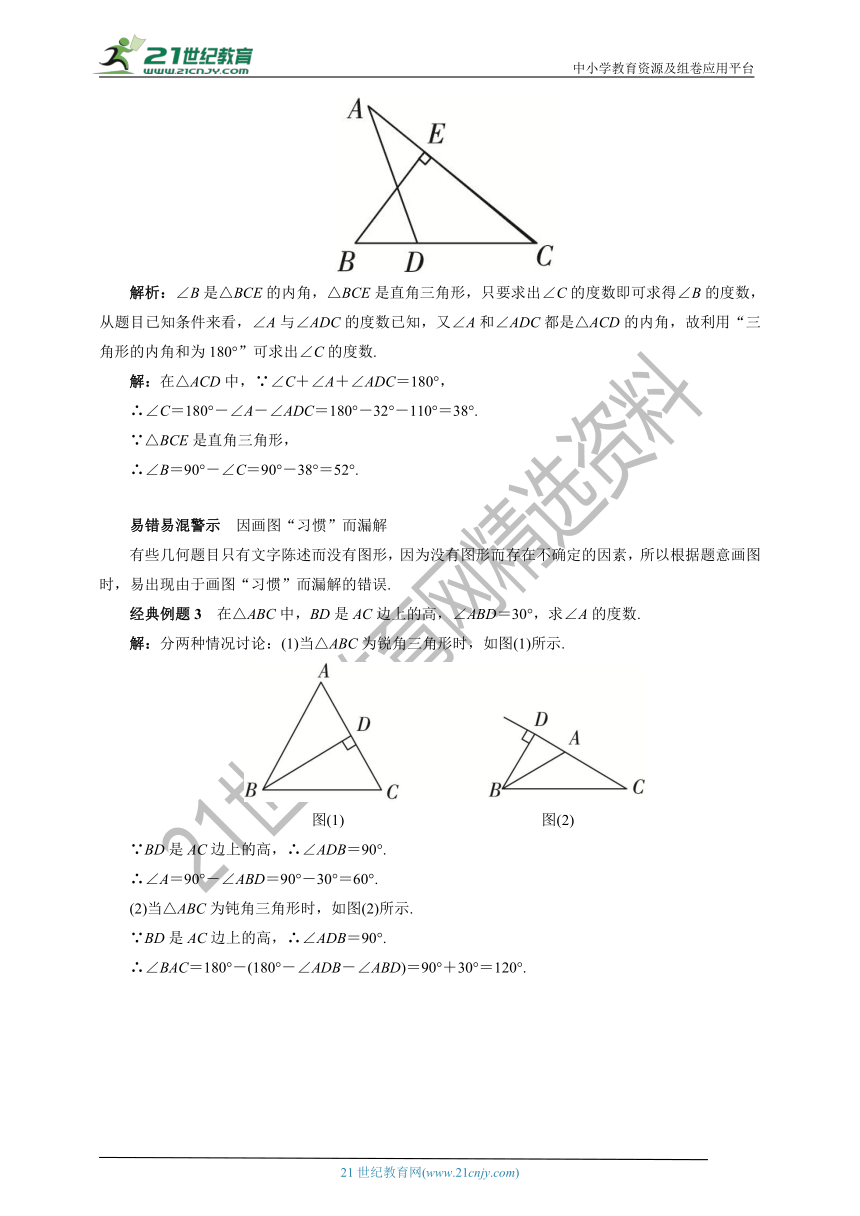
经典例题2 如图,已知∠A=32°,∠ADC=110°,BE⊥AC于点E,求∠B的度数.
解析:∠B是△BCE的内角,△BCE是直角三角形,只要求出∠C的度数即可求得∠B的度数,从题目已知条件来看,∠A与∠ADC的度数已知,又∠A和∠ADC都是△ACD的内角,故利用“三角形的内角和为180°”可求出∠C的度数.
解:在△ACD中,∵∠C+∠A+∠ADC=180°,
∴∠C=180°-∠A-∠ADC=180°-32°-110°=38°.
∵△BCE是直角三角形,
∴∠B=90°-∠C=90°-38°=52°.
易错易混警示 因画图“习惯”而漏解
有些几何题目只有文字陈述而没有图形,因为没有图形而存在不确定的因素,所以根据题意画图时,易出现由于画图“习惯”而漏解的错误.
经典例题3 在△ABC中,BD是AC边上的高,∠ABD=30°,求∠A的度数.
解:分两种情况讨论:(1)当△ABC为锐角三角形时,如图(1)所示.
图(1) 图(2)
∵BD是AC边上的高,∴∠ADB=90°.
∴∠A=90°-∠ABD=90°-30°=60°.
(2)当△ABC为钝角三角形时,如图(2)所示.
∵BD是AC边上的高,∴∠ADB=90°.
∴∠BAC=180°-(180°-∠ADB-∠ABD)=90°+30°=120°.
当 堂 检 测
1. 在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A. 35° B. 40° C. 45° D. 55°
2. 已知△ABC中,∠A=20°,∠B=∠C,那么三角形△ABC是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等边三角形
3. 如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是( )
A. 35° B. 55° C. 60° D. 70°
第3题 第4题
4. 如图,在△ABC中,∠ACB=90°,且∠A≠∠B,CD⊥AB,垂足为D,下列结论错误的是( )
A. 图中有三个直角三角形 B. ∠1=∠2
C. ∠1和∠B都是∠A的余角 D. ∠2=∠A
5. 如图,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B,C处开工挖出“V”字形通道,如果∠DBA=120°,∠ECA=135°,则∠A的度数是 .
6. 如图,在△ABC中,BD为△ABC的角平分线,如果∠A=47°,∠ADB=116°,求∠ABC和∠C的度数.
7. 如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.
当堂检测参考答案
1. C 2. A 3. D 4. B
5. 75°
6. 解:∵∠A=47°,∠ADB=116°,∴∠ABD=180°-47°-116°=17°.∵BD为△ABC的角平分线,∴∠ABC=2∠ABD=34°,∴∠C=180°-47°-34°=99°.
7. 解:∵∠AFD=158°,∴∠DFC=180°-∠AFD=22°.∵FD⊥BC,∴∠FDC=90°,∵DE⊥AB,
第十一章 三角形
11.2 与三角形有关的角
11.2.1 三角形的内角
要 点 讲 解
要点一 三角形的内角和定理
1. 三角形三个内角的和等于180°.
2. 定理的推理证明:
如图,过点B作BD∥AC.根据两直线平行,内错角相等,可得∠1=∠A.
又根据两直线平行,同旁内角互补,可得∠1+∠ABC+∠C=180°,所以∠A+∠ABC+∠C=180°.
在探究三角形内角和定理时,采用了转化的数学思想.
经典例题1 已知,在△ABC中,∠B=3∠A,∠C=5∠A.求∠A,∠B,∠C的度数.
解析:根据三角形内角和定理及已知条件求出∠A的度数,即可得出∠B,∠C的度数.
解:根据三角形内角和定理及已知条件,得∠A+3∠A+5∠A=180°.
所以∠A=20°,所以∠B=60°,∠C=100°.
要点二 直角三角形的性质与判定
性质:直角三角形的两个锐角互余.
判定:
1. 三角形有一个角是直角;
2. 有两个角互余的三角形是直角三角形.
在三角形中,两个锐角互余的前提条件必须是在直角三角形中,若△ABC是直角三角形(∠C为直角),则∠A+∠B=90°;反之,若在△ABC中,∠A+∠B=90°,则△ABC为直角三角形,直角三角形ABC也可以写成Rt△ABC.
经典例题2 如图,已知∠A=32°,∠ADC=110°,BE⊥AC于点E,求∠B的度数.
解析:∠B是△BCE的内角,△BCE是直角三角形,只要求出∠C的度数即可求得∠B的度数,从题目已知条件来看,∠A与∠ADC的度数已知,又∠A和∠ADC都是△ACD的内角,故利用“三角形的内角和为180°”可求出∠C的度数.
解:在△ACD中,∵∠C+∠A+∠ADC=180°,
∴∠C=180°-∠A-∠ADC=180°-32°-110°=38°.
∵△BCE是直角三角形,
∴∠B=90°-∠C=90°-38°=52°.
易错易混警示 因画图“习惯”而漏解
有些几何题目只有文字陈述而没有图形,因为没有图形而存在不确定的因素,所以根据题意画图时,易出现由于画图“习惯”而漏解的错误.
经典例题3 在△ABC中,BD是AC边上的高,∠ABD=30°,求∠A的度数.
解:分两种情况讨论:(1)当△ABC为锐角三角形时,如图(1)所示.
图(1) 图(2)
∵BD是AC边上的高,∴∠ADB=90°.
∴∠A=90°-∠ABD=90°-30°=60°.
(2)当△ABC为钝角三角形时,如图(2)所示.
∵BD是AC边上的高,∴∠ADB=90°.
∴∠BAC=180°-(180°-∠ADB-∠ABD)=90°+30°=120°.
当 堂 检 测
1. 在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A. 35° B. 40° C. 45° D. 55°
2. 已知△ABC中,∠A=20°,∠B=∠C,那么三角形△ABC是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等边三角形
3. 如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是( )
A. 35° B. 55° C. 60° D. 70°
第3题 第4题
4. 如图,在△ABC中,∠ACB=90°,且∠A≠∠B,CD⊥AB,垂足为D,下列结论错误的是( )
A. 图中有三个直角三角形 B. ∠1=∠2
C. ∠1和∠B都是∠A的余角 D. ∠2=∠A
5. 如图,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B,C处开工挖出“V”字形通道,如果∠DBA=120°,∠ECA=135°,则∠A的度数是 .
6. 如图,在△ABC中,BD为△ABC的角平分线,如果∠A=47°,∠ADB=116°,求∠ABC和∠C的度数.
7. 如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.
当堂检测参考答案
1. C 2. A 3. D 4. B
5. 75°
6. 解:∵∠A=47°,∠ADB=116°,∴∠ABD=180°-47°-116°=17°.∵BD为△ABC的角平分线,∴∠ABC=2∠ABD=34°,∴∠C=180°-47°-34°=99°.
7. 解:∵∠AFD=158°,∴∠DFC=180°-∠AFD=22°.∵FD⊥BC,∴∠FDC=90°,∵DE⊥AB,
