沪科版数学七上4.5 角的比较与补(余)角课件(32张PPT)
文档属性
| 名称 | 沪科版数学七上4.5 角的比较与补(余)角课件(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-16 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
4.5 角的比较与补(余)角
第4章 直线与角
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.会比较角的大小,理解两个角的和、差、倍、分的意义.(重点)
2.了解角平分线的概念,会进行相关的计算.(难点)
3.在具体情境中认识余角和补角,掌握余角和补角的性质并能运用其进行简单的推理.(重点)
导入新课
成功永远属于肯攀高峰的人
!
选择从哪一面上山会感觉到舒缓呢?
讲授新课
合作探究
类比线段长短的比较方法,你认为该如何比较两个角的大小?
角的大小比较:度量法、叠合法
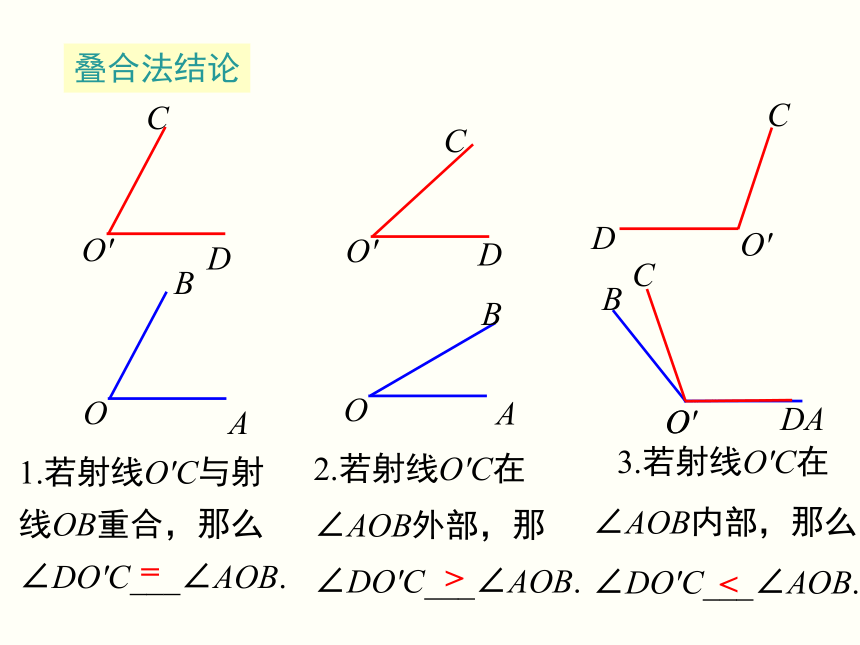
叠合法结论
1.若射线O'C与射线OB重合,那么∠DO'C___∠AOB.
2.若射线O'C在∠AOB外部,那∠DO'C___∠AOB.
3.若射线O'C在∠AOB内部,那么∠DO'C___∠AOB.
=
>
<
1.角的大小与两边画出部分的长短是否相关?
2.一个30°的角用能放大3倍的放大镜观看,看到的角度有何变化?
议一议
结论:角的两边张开越大,角就越大,与所画边的长短无关.
典例精析
例1 如图,求解下列问题:
(1)试比较∠AOC与∠BOC,∠BOD与∠COD的大小;
(2)将∠AOC写成两个角的和与两个角的差的式.
解:(1)由图可看出:∠AOC>∠BOC,(OB在∠AOC内);∠BOD>∠COD.(OC在∠B内)
(2)∠AOC=∠AOB+∠BOC;
∠AOC=∠AOD-∠DOC.
例2 根据下图,回答下列问题:
(1)试比较∠AOB,∠AOD,∠AOE,∠AOC的大小,并找出其中的锐角、直角、钝角、平角;
(2)在图中找出角的三个等量关系.
[解析] ∠AOB是平角,∠AOC是钝角,∠AOD是直角,∠AOE是锐角,于是就可找到这几个角的大小关系.
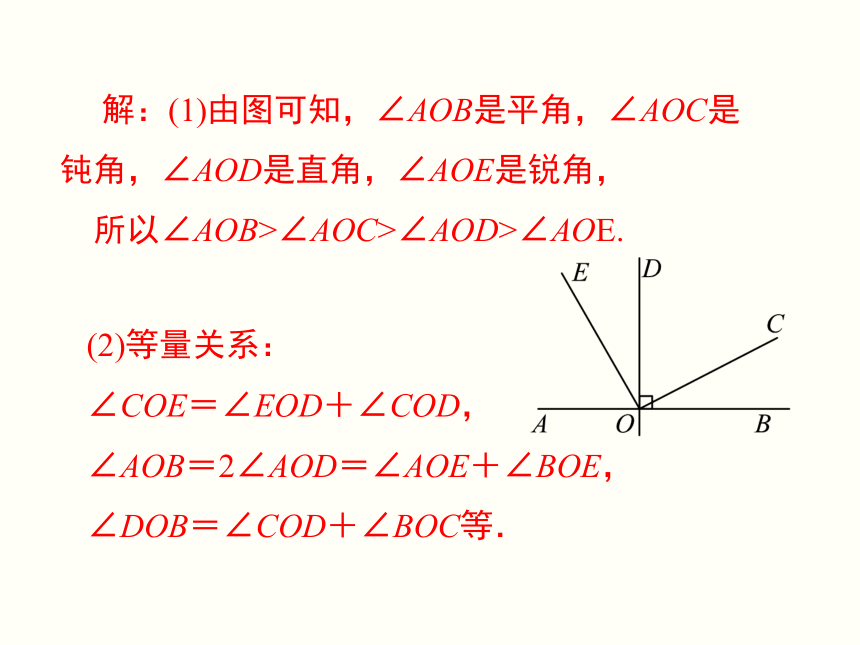
解:(1)由图可知,∠AOB是平角,∠AOC是钝角,∠AOD是直角,∠AOE是锐角,
所以∠AOB>∠AOC>∠AOD>∠AOE.
(2)等量关系:
∠COE=∠EOD+∠COD,
∠AOB=2∠AOD=∠AOE+∠BOE,∠DOB=∠COD+∠BOC等.
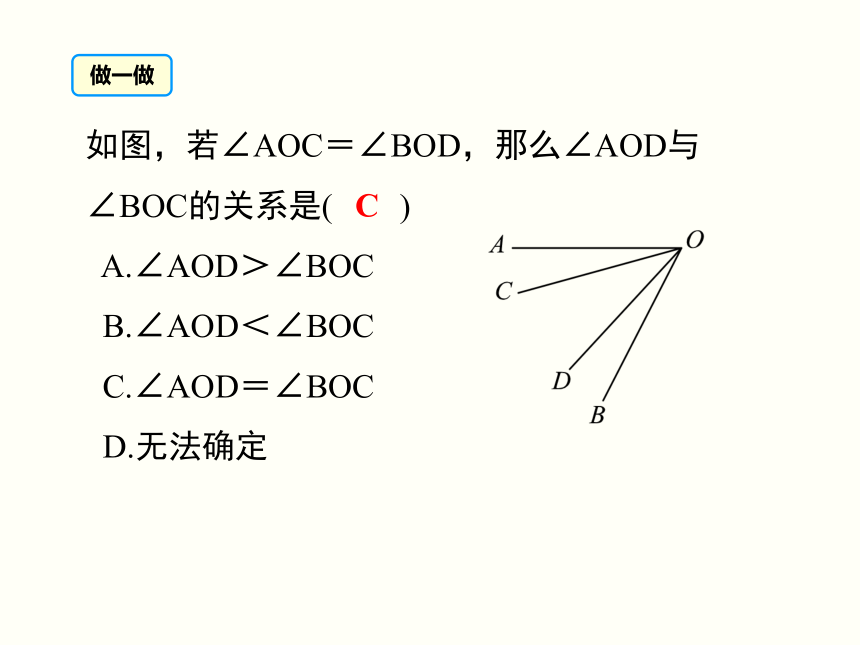
做一做
C
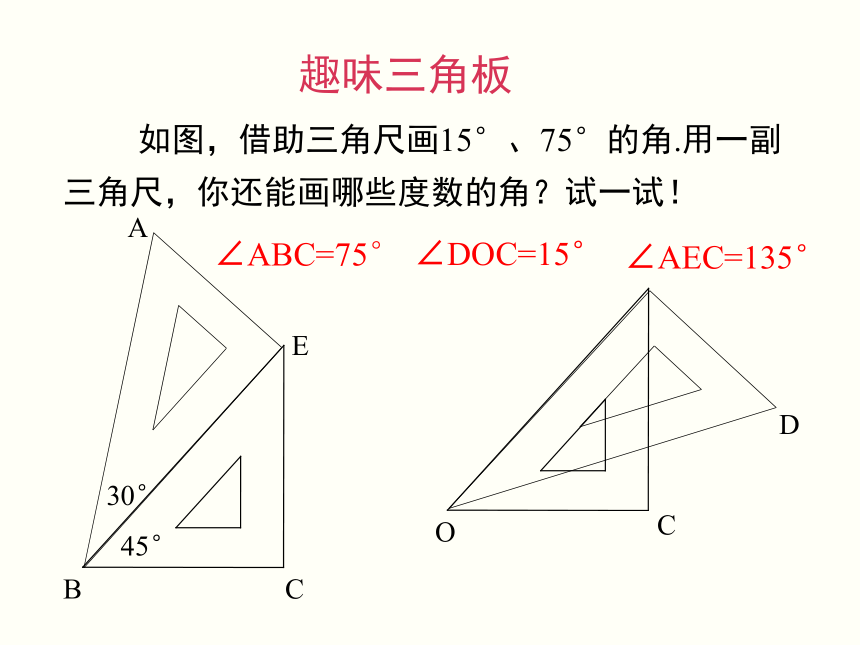
如图,借助三角尺画15°、75°的角.用一副三角尺,你还能画哪些度数的角?试一试!
∠ABC=75°
∠DOC=15°
∠AEC=135°
趣味三角板
∠ABC=105°
∠AOC=120°
∠EFG=150°
活动:大家在练习本上画一个角,然后把角的两边对折,展开以后你会发现折痕把角分成了两个角,这两个角有什么关系呢,它们又和原来的角有着怎样的等量关系?
观察思考
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
因为OC是∠AOB的平分线,
所以∠AOC =∠BOC = ∠AOB
或∠AOB =2∠BOC =2∠AOC
几何语言
C
例3 如图,点O为直线AB上一点,OM,ON分别是∠AOC,∠BOC的平分线,求∠MON的度数.
在有关角的计算中,几何图形与等式的性质同时使用,问题会迎刃而解.
解:因为点A,O,B在一条直线上,
所以∠AOB=180°.
因为∠AOC+∠BOC=∠AOB,
所以∠AOC+∠BOC=180°.
又因为OM,ON分别是∠AOC和∠BOC的平分线,
所以∠MOC= ∠AOC,∠CON= ∠BOC.
所以∠MOC+∠CON= (∠AOC+∠BOC)=
×180°=90°.
又因为∠MON=∠MOC+∠CON,
∴∠MON=90°.
做一做
如图,∠AOB=90°,OE,OC分别是∠AOD,∠DOB的平分线,则∠EOC=________°.
45
2
1
如果两个角的和等于一个直角,就说这两个角互为余角(简称互余).
如图,可以说∠1是∠2的余角或∠2是∠1的余角.
定义
图中给出的各角,那些互为余角?
15o
24o
66o
75o
46.2o
43.8o
试一试
3
4
如果两个角的和等于一个平角,就说这两个角互为补角(简称互补).
如图,可以说∠3是∠4的余角或∠4是∠3的补角.
定义
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
试一试
思考:∠1与∠2,∠3都互为补角,∠2与∠3的大小有什么关系?
同角(等角)的补角相等
结论:
∠2=180°-∠1
∠3=180°-∠1
同角(等角)的余角相等
类似可得:
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
结论: 同一个锐角的补角比它的余角大_____.
填一填
90°
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
x°(x<90)
例3 如图,∠1=∠3,∠1与∠2互补,∠3与∠4互补,那么∠2与∠4有什么关系?
解:因为∠1与∠2互补,所以∠2=180°-∠1.
因为∠3与∠4互补,所以∠4=180°-∠3.
又因为∠1=∠3,所以∠2=∠4.
解:因为∠AOC=∠BOD=90°,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
所以∠AOB,∠COD都是∠BOC的余角,
所以∠AOB=∠COD.
因为∠AOB=40°,所以∠COD=40°.
例5 一个角的补角比它的余角的2倍多12°,求这个角的度数.
解:设这个角的度数为x°.
所以它的补角为(180-x)°,
它的余角为(90-x)°,
依题意,得 180-x=2(90-x)+12.
解方程,得 x=12.
答:这个角的度数为12°.
如图,将长方形ABCD沿EF折叠,C点落在C′处,D点落在D′处.若∠EFC=119°,则∠BFC′为( )A.58° B.45°
C.60° D.42°
解析:∵将长方形ABCD沿EF折叠,C点落在C′处,D点落在D′处,∠EFC=119°,∴∠EFC′=∠EFC=119°,∠EFB=180°-∠EFC=61°,∴∠BFC′=∠EFC′-∠EFB=119°-61°=58°.
A
拓展提升
1.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
25
当堂练习
2.如图,∠1=∠3,那么( ).
A.∠1=∠2 B. ∠2=∠3
C.∠AOC=∠BOD D. ∠1=
C
3.如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD等于( )
A.30° B.35°
C.20° D.40°
B
4. 若一个角的补角等于它的余角的4 倍,求这个角的度数.
解:设这个角是x°,则它的补角是(180°-x°),余角是(90°-x°) .
根据题意,得
180°-x°= 4 (90°-x°)
解得 x=60
答:这个角的度数是60 °.
课堂小结
角的比较
角的比较
角平分线
互余与互补
度量法
叠合法
概念
与角有关的和、差、倍、分的计算
互余:两角之和为直角
互补:两角之和为平角
性质:同(等)角的补(余)相等.
4.5 角的比较与补(余)角
第4章 直线与角
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.会比较角的大小,理解两个角的和、差、倍、分的意义.(重点)
2.了解角平分线的概念,会进行相关的计算.(难点)
3.在具体情境中认识余角和补角,掌握余角和补角的性质并能运用其进行简单的推理.(重点)
导入新课
成功永远属于肯攀高峰的人
!
选择从哪一面上山会感觉到舒缓呢?
讲授新课
合作探究
类比线段长短的比较方法,你认为该如何比较两个角的大小?
角的大小比较:度量法、叠合法
叠合法结论
1.若射线O'C与射线OB重合,那么∠DO'C___∠AOB.
2.若射线O'C在∠AOB外部,那∠DO'C___∠AOB.
3.若射线O'C在∠AOB内部,那么∠DO'C___∠AOB.
=
>
<
1.角的大小与两边画出部分的长短是否相关?
2.一个30°的角用能放大3倍的放大镜观看,看到的角度有何变化?
议一议
结论:角的两边张开越大,角就越大,与所画边的长短无关.
典例精析
例1 如图,求解下列问题:
(1)试比较∠AOC与∠BOC,∠BOD与∠COD的大小;
(2)将∠AOC写成两个角的和与两个角的差的式.
解:(1)由图可看出:∠AOC>∠BOC,(OB在∠AOC内);∠BOD>∠COD.(OC在∠B内)
(2)∠AOC=∠AOB+∠BOC;
∠AOC=∠AOD-∠DOC.
例2 根据下图,回答下列问题:
(1)试比较∠AOB,∠AOD,∠AOE,∠AOC的大小,并找出其中的锐角、直角、钝角、平角;
(2)在图中找出角的三个等量关系.
[解析] ∠AOB是平角,∠AOC是钝角,∠AOD是直角,∠AOE是锐角,于是就可找到这几个角的大小关系.
解:(1)由图可知,∠AOB是平角,∠AOC是钝角,∠AOD是直角,∠AOE是锐角,
所以∠AOB>∠AOC>∠AOD>∠AOE.
(2)等量关系:
∠COE=∠EOD+∠COD,
∠AOB=2∠AOD=∠AOE+∠BOE,∠DOB=∠COD+∠BOC等.
做一做
C
如图,借助三角尺画15°、75°的角.用一副三角尺,你还能画哪些度数的角?试一试!
∠ABC=75°
∠DOC=15°
∠AEC=135°
趣味三角板
∠ABC=105°
∠AOC=120°
∠EFG=150°
活动:大家在练习本上画一个角,然后把角的两边对折,展开以后你会发现折痕把角分成了两个角,这两个角有什么关系呢,它们又和原来的角有着怎样的等量关系?
观察思考
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
因为OC是∠AOB的平分线,
所以∠AOC =∠BOC = ∠AOB
或∠AOB =2∠BOC =2∠AOC
几何语言
C
例3 如图,点O为直线AB上一点,OM,ON分别是∠AOC,∠BOC的平分线,求∠MON的度数.
在有关角的计算中,几何图形与等式的性质同时使用,问题会迎刃而解.
解:因为点A,O,B在一条直线上,
所以∠AOB=180°.
因为∠AOC+∠BOC=∠AOB,
所以∠AOC+∠BOC=180°.
又因为OM,ON分别是∠AOC和∠BOC的平分线,
所以∠MOC= ∠AOC,∠CON= ∠BOC.
所以∠MOC+∠CON= (∠AOC+∠BOC)=
×180°=90°.
又因为∠MON=∠MOC+∠CON,
∴∠MON=90°.
做一做
如图,∠AOB=90°,OE,OC分别是∠AOD,∠DOB的平分线,则∠EOC=________°.
45
2
1
如果两个角的和等于一个直角,就说这两个角互为余角(简称互余).
如图,可以说∠1是∠2的余角或∠2是∠1的余角.
定义
图中给出的各角,那些互为余角?
15o
24o
66o
75o
46.2o
43.8o
试一试
3
4
如果两个角的和等于一个平角,就说这两个角互为补角(简称互补).
如图,可以说∠3是∠4的余角或∠4是∠3的补角.
定义
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
试一试
思考:∠1与∠2,∠3都互为补角,∠2与∠3的大小有什么关系?
同角(等角)的补角相等
结论:
∠2=180°-∠1
∠3=180°-∠1
同角(等角)的余角相等
类似可得:
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
结论: 同一个锐角的补角比它的余角大_____.
填一填
90°
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
x°(x<90)
例3 如图,∠1=∠3,∠1与∠2互补,∠3与∠4互补,那么∠2与∠4有什么关系?
解:因为∠1与∠2互补,所以∠2=180°-∠1.
因为∠3与∠4互补,所以∠4=180°-∠3.
又因为∠1=∠3,所以∠2=∠4.
解:因为∠AOC=∠BOD=90°,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
所以∠AOB,∠COD都是∠BOC的余角,
所以∠AOB=∠COD.
因为∠AOB=40°,所以∠COD=40°.
例5 一个角的补角比它的余角的2倍多12°,求这个角的度数.
解:设这个角的度数为x°.
所以它的补角为(180-x)°,
它的余角为(90-x)°,
依题意,得 180-x=2(90-x)+12.
解方程,得 x=12.
答:这个角的度数为12°.
如图,将长方形ABCD沿EF折叠,C点落在C′处,D点落在D′处.若∠EFC=119°,则∠BFC′为( )A.58° B.45°
C.60° D.42°
解析:∵将长方形ABCD沿EF折叠,C点落在C′处,D点落在D′处,∠EFC=119°,∴∠EFC′=∠EFC=119°,∠EFB=180°-∠EFC=61°,∴∠BFC′=∠EFC′-∠EFB=119°-61°=58°.
A
拓展提升
1.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
25
当堂练习
2.如图,∠1=∠3,那么( ).
A.∠1=∠2 B. ∠2=∠3
C.∠AOC=∠BOD D. ∠1=
C
3.如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD等于( )
A.30° B.35°
C.20° D.40°
B
4. 若一个角的补角等于它的余角的4 倍,求这个角的度数.
解:设这个角是x°,则它的补角是(180°-x°),余角是(90°-x°) .
根据题意,得
180°-x°= 4 (90°-x°)
解得 x=60
答:这个角的度数是60 °.
课堂小结
角的比较
角的比较
角平分线
互余与互补
度量法
叠合法
概念
与角有关的和、差、倍、分的计算
互余:两角之和为直角
互补:两角之和为平角
性质:同(等)角的补(余)相等.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
