沪科版初中数学第 4章 直线与角小结与复习课件(26张ppt)
文档属性
| 名称 | 沪科版初中数学第 4章 直线与角小结与复习课件(26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 605.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-13 12:21:04 | ||
图片预览







文档简介
(共26张PPT)
小结与复习
第4章 直线与角
要点梳理
考点讲练
课堂小结
课后作业
要点梳理
一、几何图形
1.几何图形都是由点、线、面、体组成的.
2.点、线、面、体之间的联系
(1)体是由面围成,面与面相交成线,线与线相交成点
(2)点动成线、线动成面、面动成体
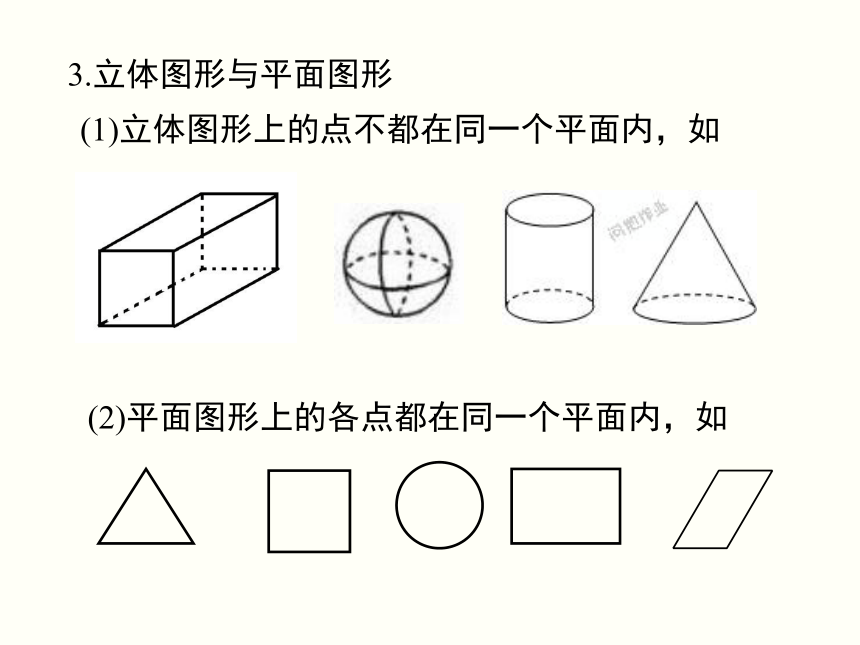
(2)平面图形上的各点都在同一个平面内,如
3.立体图形与平面图形
(1)立体图形上的点不都在同一个平面内,如
二、直线、射线、线段
1.有关直线的基本事实
经过两点有一条直线,并且只有一条直线.
2.直线、射线、线段的区别
端点个数
2个
不能延伸
延伸性
能否度量
可度量
1个
向一个方向
无限延伸
不可度量
无端点
向两个方向
无限延伸
不可度量
类型
线段
射线
直线
4.有关线段的基本事实
两点之间线段最短
3.线段的中点
应用格式:
5.线段长短的比较方法
度量法或叠合法
三、角
1.角的定义
(1)从一个点出发的两条射线组成的图形,叫做角
(2)角也可以看做由一条射线绕着它的端点旋转所形成的图形
2.角的度量
度、分、秒的互化
1″=(1/60)′,1′=(1/60)°
1°=60′,1′=60″
3.角的大小的比较方法
度量法或叠合法
4.角的平分线
C
OC是∠AOB的角平分线,
∠AOC =∠BOC =1/2∠AOB
∠AOB =2∠BOC =2∠AOC
应用格式:
5.余角与补角的性质
同角(等角)的补角相等
同角(等角)的与角相等
考点讲练
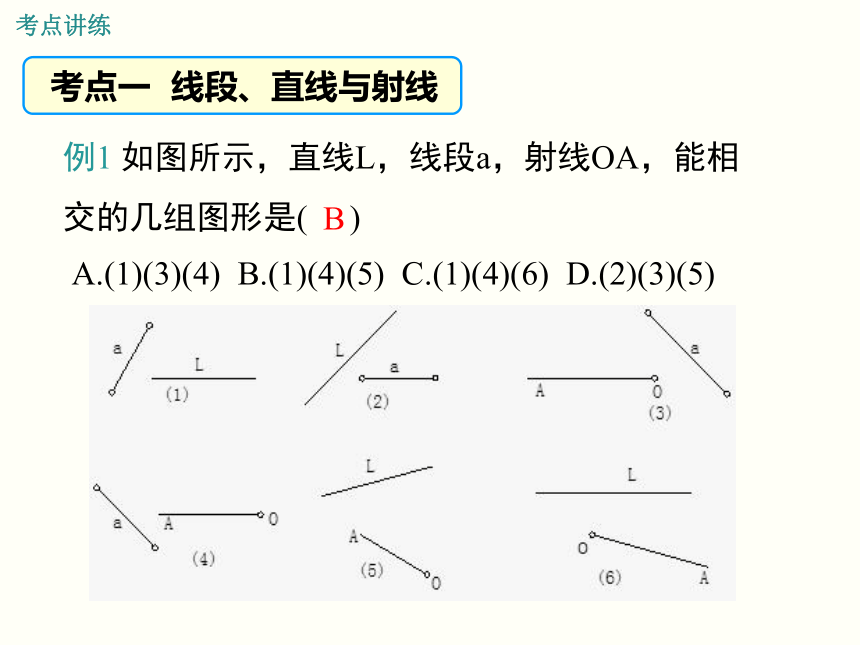
例1 如图所示,直线L,线段a,射线OA,能相交的几组图形是(???? )
A.(1)(3)(4) B.(1)(4)(5) C.(1)(4)(6) D.(2)(3)(5)
B
解析:(2)中直线L与线段a不相交,(3)中线段a与射线OA不相交,(6)中直线L与射线OA不相交.故选B.
提示:直线可以向两边无限延伸,射线只能向一个方向无限延伸,线段有两个端点,不能延伸.
解析:此题相当于一条线段上有3个点,有多少种不同的票价即有多少条线段:4+3+2+1=10;有多少种车票是要考虑顺序的,则有10×2=20.
1.往返于甲、乙两地的火车中途要停靠三个站,则有_______种不同的票价(来回票价一样),需准备_______种车票.
10
20
例2 如图,点C在线段AB上,点M、N分别
是AC、BC的中点.
(1)AC = 8 cm,CB = 6 cm,求线段MN的长;
【解析】根据“M、N分别是AC、BC的中点”,先求出MC,CN的长度,再利用MN=CM+CN即可求出MN的长度.
解:(1)∵点M、N分别是AC、BC的中点,∴CM=1/2AC=4(cm),CN=1/2BC=3cm,
∴MN=CM+CN=4+3=7 (cm);
(2)若C为线段AB上任一点,满足AC + CB = a cm,其它条件不变,你能猜想MN的长度吗?并说明理由.
解:(2)同(1)可得
CM=1/2AC ,CN=1/2BC,
∴MN=CM+CN
=1/2AC+1/2BC
=1/2(AC+BC)=1/2a (cm)
(3)若C在线段AB的延长线上,且满足AC-BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.
解:MN的长度等于1/2b(cm).
根据题意画出图形,
由图可得
MN=MC-NC=1/2AC-1/2BC
=1/2(AC-BC)= 1/2b(cm).
2.点A,B,C 在同一条直线上,AB=3 cm,
BC=1 cm.求AC的长.
解:(1)如图①,因AB=3cm,BC=1cm,
所以,AC=AB+BC=3+1=4(cm).
(2)如图②,AC=AB-BC=3-1=2(cm).
【解析】因点A,B,C的顺序不确定,所以分B在线段AC上,B在线段AC的延长线上两种情况 .
例3. 45°52′48″=______°;
126.31°= ____°____′____″;
25°18′÷3=__________;
126.31?=126?+0.31×60′=126?+18.6′
=126?18′+0.6×60″=126?18′36″
解析:45°52′48″=45°+52′+(48/60)′=45°+52.8′
=45?+(52.8/60)°=45.88?
25°18′÷3=8°+1°18′÷3=8°+78′÷3=8°26′
3.若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
A
4. 5点整时,时钟上时针与分钟之间的夹角是( )
A.210° B.30° C.150° D.60°
C
例4.如图,∠AOB是直角∠AOC=50°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小;
【解析】先求出∠BOC的度数,再根据角平分线的定义求出∠COM,∠CON,然后根据∠MON=∠COM-∠CON代入数据进行计算即可得解.
解:(1)∵∠AOB是直角,∠AOC=50°, ∴∠BOC=∠AOB+∠AOC=90°+50°=140°, ∵ON是∠AOC的平分线,OM是∠BOC的平分线, ∴∠COM=1/2∠BOC=1/2×140°=70°, ∠CON=1/2∠AOC=1/2×50°=25°, ∴∠MON=∠COM-∠CON=70°-25°=45°;
(2)当∠AOC=α时, ∠MON等于多少度?
(2)∠BOC=∠AOB+∠AOC=90°+α, ∵ON是∠AOC的平分线,OM是∠BOC的平分线, ∴∠COM=1/2∠BOC=1/2(90°+α), ∠CON=1/2∠AOC=1/2α, ∴∠MON=∠COM-∠CON
=1/2(90°+α)-α=45°
(3)当锐角∠AOC的大小发生改变时,
∠MON的大小也会发生改变吗?为什么?
(3)不会发生变化.
由(2)可知∠MON的大小与∠AOC无关,总是等于∠AOB的一半.
5. 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B'处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A'处,得折痕EN,求∠NEM的度数.
解:由折纸过程可知, EM平分∠BEB' , EN平分∠AEA'.
因 ∠BEB'+∠AEA'=180°,
所以有∠NEM=∠NEA'+∠MEB'
例5 已知∠α和∠β互为补角,并且∠β的一半比∠α小30?,求∠α、∠β.
解:设∠α=x?,则∠β=180?-x?.
根据题意 ∠β=2(∠α-30?),
即 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80?,∠β=100?.
【解析】设∠α=x?,用x表示出∠β,列出方程即可.
6.互为余角的两个角之差为35°,则较大角的补角是________.
117.5°
直线与角
几何图形
立体图形
平面图形
概念与性质
运算
直线、射线、线段
角
尺规作图
两点确定一条直线
两点之间线段最短
线段的中点
角平分线
互为余(补)角的概念与性质
线段(角)的和、差、倍、分
线段的和、差、倍、分计算
角的和、差、倍、分计算
度、分、秒的转化
课堂小结
见章末练习
课后作业
小结与复习
第4章 直线与角
要点梳理
考点讲练
课堂小结
课后作业
要点梳理
一、几何图形
1.几何图形都是由点、线、面、体组成的.
2.点、线、面、体之间的联系
(1)体是由面围成,面与面相交成线,线与线相交成点
(2)点动成线、线动成面、面动成体
(2)平面图形上的各点都在同一个平面内,如
3.立体图形与平面图形
(1)立体图形上的点不都在同一个平面内,如
二、直线、射线、线段
1.有关直线的基本事实
经过两点有一条直线,并且只有一条直线.
2.直线、射线、线段的区别
端点个数
2个
不能延伸
延伸性
能否度量
可度量
1个
向一个方向
无限延伸
不可度量
无端点
向两个方向
无限延伸
不可度量
类型
线段
射线
直线
4.有关线段的基本事实
两点之间线段最短
3.线段的中点
应用格式:
5.线段长短的比较方法
度量法或叠合法
三、角
1.角的定义
(1)从一个点出发的两条射线组成的图形,叫做角
(2)角也可以看做由一条射线绕着它的端点旋转所形成的图形
2.角的度量
度、分、秒的互化
1″=(1/60)′,1′=(1/60)°
1°=60′,1′=60″
3.角的大小的比较方法
度量法或叠合法
4.角的平分线
C
OC是∠AOB的角平分线,
∠AOC =∠BOC =1/2∠AOB
∠AOB =2∠BOC =2∠AOC
应用格式:
5.余角与补角的性质
同角(等角)的补角相等
同角(等角)的与角相等
考点讲练
例1 如图所示,直线L,线段a,射线OA,能相交的几组图形是(???? )
A.(1)(3)(4) B.(1)(4)(5) C.(1)(4)(6) D.(2)(3)(5)
B
解析:(2)中直线L与线段a不相交,(3)中线段a与射线OA不相交,(6)中直线L与射线OA不相交.故选B.
提示:直线可以向两边无限延伸,射线只能向一个方向无限延伸,线段有两个端点,不能延伸.
解析:此题相当于一条线段上有3个点,有多少种不同的票价即有多少条线段:4+3+2+1=10;有多少种车票是要考虑顺序的,则有10×2=20.
1.往返于甲、乙两地的火车中途要停靠三个站,则有_______种不同的票价(来回票价一样),需准备_______种车票.
10
20
例2 如图,点C在线段AB上,点M、N分别
是AC、BC的中点.
(1)AC = 8 cm,CB = 6 cm,求线段MN的长;
【解析】根据“M、N分别是AC、BC的中点”,先求出MC,CN的长度,再利用MN=CM+CN即可求出MN的长度.
解:(1)∵点M、N分别是AC、BC的中点,∴CM=1/2AC=4(cm),CN=1/2BC=3cm,
∴MN=CM+CN=4+3=7 (cm);
(2)若C为线段AB上任一点,满足AC + CB = a cm,其它条件不变,你能猜想MN的长度吗?并说明理由.
解:(2)同(1)可得
CM=1/2AC ,CN=1/2BC,
∴MN=CM+CN
=1/2AC+1/2BC
=1/2(AC+BC)=1/2a (cm)
(3)若C在线段AB的延长线上,且满足AC-BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.
解:MN的长度等于1/2b(cm).
根据题意画出图形,
由图可得
MN=MC-NC=1/2AC-1/2BC
=1/2(AC-BC)= 1/2b(cm).
2.点A,B,C 在同一条直线上,AB=3 cm,
BC=1 cm.求AC的长.
解:(1)如图①,因AB=3cm,BC=1cm,
所以,AC=AB+BC=3+1=4(cm).
(2)如图②,AC=AB-BC=3-1=2(cm).
【解析】因点A,B,C的顺序不确定,所以分B在线段AC上,B在线段AC的延长线上两种情况 .
例3. 45°52′48″=______°;
126.31°= ____°____′____″;
25°18′÷3=__________;
126.31?=126?+0.31×60′=126?+18.6′
=126?18′+0.6×60″=126?18′36″
解析:45°52′48″=45°+52′+(48/60)′=45°+52.8′
=45?+(52.8/60)°=45.88?
25°18′÷3=8°+1°18′÷3=8°+78′÷3=8°26′
3.若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
A
4. 5点整时,时钟上时针与分钟之间的夹角是( )
A.210° B.30° C.150° D.60°
C
例4.如图,∠AOB是直角∠AOC=50°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小;
【解析】先求出∠BOC的度数,再根据角平分线的定义求出∠COM,∠CON,然后根据∠MON=∠COM-∠CON代入数据进行计算即可得解.
解:(1)∵∠AOB是直角,∠AOC=50°, ∴∠BOC=∠AOB+∠AOC=90°+50°=140°, ∵ON是∠AOC的平分线,OM是∠BOC的平分线, ∴∠COM=1/2∠BOC=1/2×140°=70°, ∠CON=1/2∠AOC=1/2×50°=25°, ∴∠MON=∠COM-∠CON=70°-25°=45°;
(2)当∠AOC=α时, ∠MON等于多少度?
(2)∠BOC=∠AOB+∠AOC=90°+α, ∵ON是∠AOC的平分线,OM是∠BOC的平分线, ∴∠COM=1/2∠BOC=1/2(90°+α), ∠CON=1/2∠AOC=1/2α, ∴∠MON=∠COM-∠CON
=1/2(90°+α)-α=45°
(3)当锐角∠AOC的大小发生改变时,
∠MON的大小也会发生改变吗?为什么?
(3)不会发生变化.
由(2)可知∠MON的大小与∠AOC无关,总是等于∠AOB的一半.
5. 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B'处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A'处,得折痕EN,求∠NEM的度数.
解:由折纸过程可知, EM平分∠BEB' , EN平分∠AEA'.
因 ∠BEB'+∠AEA'=180°,
所以有∠NEM=∠NEA'+∠MEB'
例5 已知∠α和∠β互为补角,并且∠β的一半比∠α小30?,求∠α、∠β.
解:设∠α=x?,则∠β=180?-x?.
根据题意 ∠β=2(∠α-30?),
即 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80?,∠β=100?.
【解析】设∠α=x?,用x表示出∠β,列出方程即可.
6.互为余角的两个角之差为35°,则较大角的补角是________.
117.5°
直线与角
几何图形
立体图形
平面图形
概念与性质
运算
直线、射线、线段
角
尺规作图
两点确定一条直线
两点之间线段最短
线段的中点
角平分线
互为余(补)角的概念与性质
线段(角)的和、差、倍、分
线段的和、差、倍、分计算
角的和、差、倍、分计算
度、分、秒的转化
课堂小结
见章末练习
课后作业
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
