人教版数学必修5 2.1 数列的概念(共14张ppt)
文档属性
| 名称 | 人教版数学必修5 2.1 数列的概念(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 451.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-13 16:29:41 | ||
图片预览





文档简介
课件14张PPT。2.1数列的概念 教学目标
知识与技能:理解数列及其有关概念,了解数列和函数之间的关系;了解数列的通项公式,并会用通项公式写出数列的任意一项;对于比较简单的数列,会根据其前几项写出它的一个通项公式。
过程与方法:通过对一列数的观察、归纳,写出符合条件的一个通项公式,培养学生的观察能力和抽象概括能力.
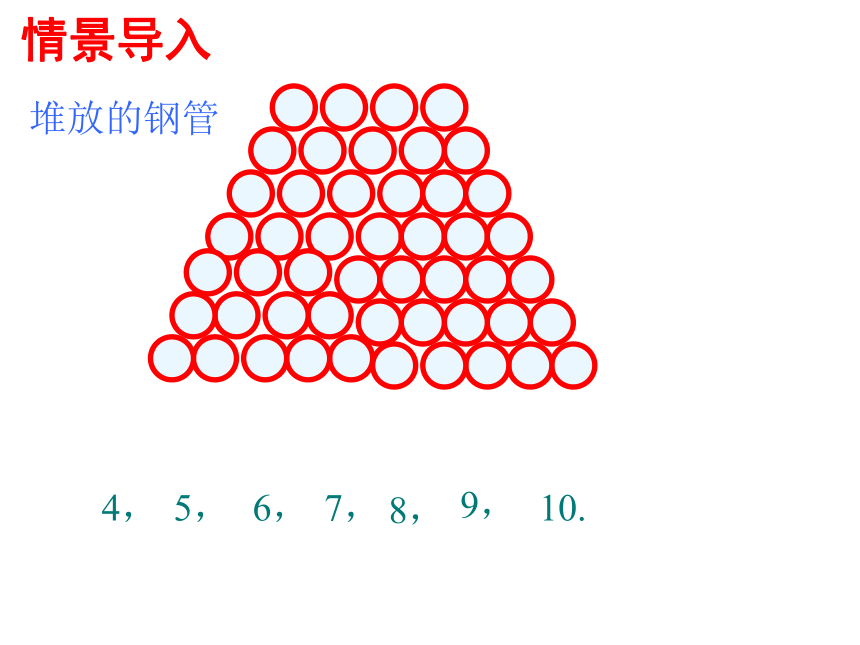
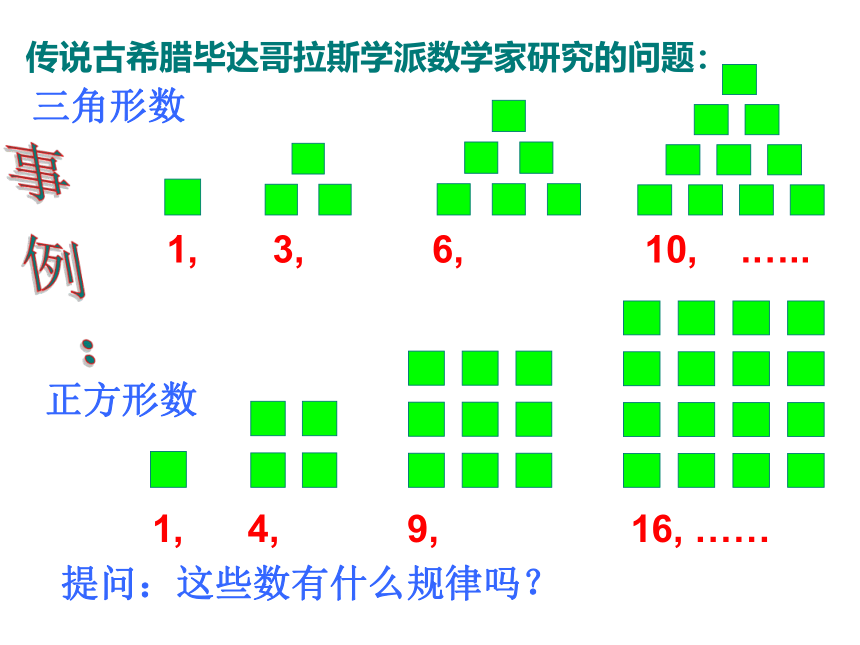
情感态度与价值观:通过本节课的学习,体会数学来源于生活,提高学生学习数学的兴趣。4,5,6,7,8,9,10.堆放的钢管情景导入三角形数1, 3, 6, 10, .….. 正方形数1, 4, 9, 16, ……传说古希腊毕达哥拉斯学派数学家研究的问题:提问:这些数有什么规律吗?事 例 : 1. 都是一列数;
2. 都有一定的顺序. 讲授新课概念:按一定顺序排列着的一列数称为数列问1:数列 ,2 , 改为13 ,… ,35 , 2 , ,… ,3531请问:是不是同一数列?问2:数列改为:-1,1,-1,1……1,-1,1,-1……,请问:是不是同一数列?不是不是(数列具有有序性)1想一想:数列与集合的区别是什么?
(1)数列 是 数 ,而集合中的元素不一定是数;
(2)数列 中的数具有有序性,而集合中的元素具有无序性;
(3)数列 中的数具有可重 复性 ,而集合中的元素不能重复,具有互异性。思考:数列与集合有何区别 (3)1,2,3,4,…,35 (1)三角形数:1,3,6,10,··· 请
观
察(5)-1,1,-1,1, …(4)1,1,1,1,…(2)1,2,3,4,…的倒数2数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项,第2项,······,第n项, ······
3数列的分类(1)按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系分:递增数列,递减数列,摆动数列,常数列。无穷数列无穷数列有穷数列无穷数列无穷数列递增数列递增数列递减数列摆动数列常数列1,3,6,10,···4 数列的一般形式可以
写成:简记为 其中是数第1项第2项第3项第n项5 的第n项
与项数之间的关系可以用一个公式来表示,列的第n项。??? 那么这个公式就叫做这个数列的通项公式。如果数列或??思 考 :根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明。? 例1:写出下面数列的一个通项公式,使它的前4项分别是下列各数:注意:①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③ 变式见导纲 1.通项公式能够很清楚的表示数列中项数和项的关系;数列的通项公式有什么用呢?2.由通项公式可以求出数列中的每一项.例2: 根据下面数列的通项公式,写出前5项.变式见导纲 对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.序号n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量)(函数值)数列是一种特殊的函数可以认为:数列与函数的关系:6 从函数的观点看, 是 的函数。
数列的项序号 数列可以看作是一个定义域为正整数集 ( 或它的有限子集{1,2,…,n})的函数, ,即当自变量从小到大依次取值时对应的一列函数值。数列的通项公式也就是相应函数的解析式
本节课学习的主要内容有:1、数列的有关概念2、数列的通项公式;3、数列的实质; 4、本节课的能力要求是:(1) 会由通项公式 求数列的任一项;(2)会用观察法由数列的前几项求数列的通项公式。
知识与技能:理解数列及其有关概念,了解数列和函数之间的关系;了解数列的通项公式,并会用通项公式写出数列的任意一项;对于比较简单的数列,会根据其前几项写出它的一个通项公式。
过程与方法:通过对一列数的观察、归纳,写出符合条件的一个通项公式,培养学生的观察能力和抽象概括能力.
情感态度与价值观:通过本节课的学习,体会数学来源于生活,提高学生学习数学的兴趣。4,5,6,7,8,9,10.堆放的钢管情景导入三角形数1, 3, 6, 10, .….. 正方形数1, 4, 9, 16, ……传说古希腊毕达哥拉斯学派数学家研究的问题:提问:这些数有什么规律吗?事 例 : 1. 都是一列数;
2. 都有一定的顺序. 讲授新课概念:按一定顺序排列着的一列数称为数列问1:数列 ,2 , 改为13 ,… ,35 , 2 , ,… ,3531请问:是不是同一数列?问2:数列改为:-1,1,-1,1……1,-1,1,-1……,请问:是不是同一数列?不是不是(数列具有有序性)1想一想:数列与集合的区别是什么?
(1)数列 是 数 ,而集合中的元素不一定是数;
(2)数列 中的数具有有序性,而集合中的元素具有无序性;
(3)数列 中的数具有可重 复性 ,而集合中的元素不能重复,具有互异性。思考:数列与集合有何区别 (3)1,2,3,4,…,35 (1)三角形数:1,3,6,10,··· 请
观
察(5)-1,1,-1,1, …(4)1,1,1,1,…(2)1,2,3,4,…的倒数2数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项,第2项,······,第n项, ······
3数列的分类(1)按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系分:递增数列,递减数列,摆动数列,常数列。无穷数列无穷数列有穷数列无穷数列无穷数列递增数列递增数列递减数列摆动数列常数列1,3,6,10,···4 数列的一般形式可以
写成:简记为 其中是数第1项第2项第3项第n项5 的第n项
与项数之间的关系可以用一个公式来表示,列的第n项。??? 那么这个公式就叫做这个数列的通项公式。如果数列或??思 考 :根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明。? 例1:写出下面数列的一个通项公式,使它的前4项分别是下列各数:注意:①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③ 变式见导纲 1.通项公式能够很清楚的表示数列中项数和项的关系;数列的通项公式有什么用呢?2.由通项公式可以求出数列中的每一项.例2: 根据下面数列的通项公式,写出前5项.变式见导纲 对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.序号n 1 2 3 4 ……64
项an 1 2 22 23 …… 263
(自变量)(函数值)数列是一种特殊的函数可以认为:数列与函数的关系:6 从函数的观点看, 是 的函数。
数列的项序号 数列可以看作是一个定义域为正整数集 ( 或它的有限子集{1,2,…,n})的函数, ,即当自变量从小到大依次取值时对应的一列函数值。数列的通项公式也就是相应函数的解析式
本节课学习的主要内容有:1、数列的有关概念2、数列的通项公式;3、数列的实质; 4、本节课的能力要求是:(1) 会由通项公式 求数列的任一项;(2)会用观察法由数列的前几项求数列的通项公式。
