人教版数学必修5 2.5 等比数列的前n项和(第一课时)(共20张ppt)
文档属性
| 名称 | 人教版数学必修5 2.5 等比数列的前n项和(第一课时)(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 401.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-13 16:33:16 | ||
图片预览








文档简介
课件20张PPT。等比数列的前n项和 (第一课时)学习目标:
1.理解并掌握等比数列前n项和公式及
其推导过程.
2.能够应用前n项和公式解决等比数列
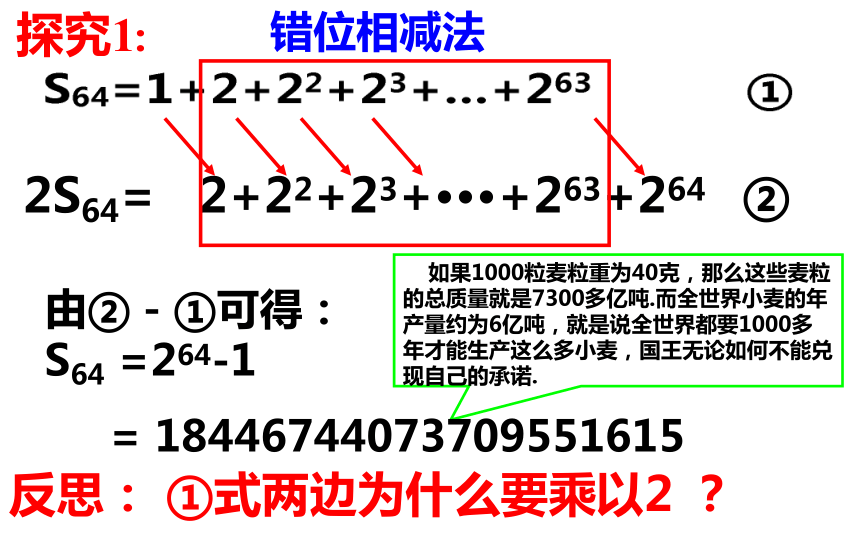
有关问题.复习引入1. 等比数列的定义:2. 等比数列通项公式:: 故事回顾讲授新课问题2:棋盘上的小麦一共有多少?问题1:棋盘上的麦粒构成什么数列? 2S64= 2+22+23+···+263+264 ② 错位相减法反思: ①式两边为什么要乘以2 ?由②-①可得:
S64 =264-1 如果1000粒麦粒重为40克,那么这些麦粒的总质量就是7300多亿吨.而全世界小麦的年产量约为6亿吨,就是说全世界都要1000多年才能生产这么多小麦,国王无论如何不能兑现自己的承诺. 探究1:= 18446744073709551615 类比探究:等比数列前n项和公式推导1①②①- ②得:正确结论:应分q=1和q ≠1讨论探究结果:探究结果:拓展探究:等比数列前n项和公式推导2理解强化小结:公式应用要明确“基本量a1、n、q”XXX例题讲解:习题讲解:拓展练习:46536例2. 某商场第一年销售计算机5000台,如果平均每年的售量比上一年增加10%,那么从第一年起,约几年内可使总销售量达到30000台(保留到个位 lg1.6=0.2,lg1.1=0.041)?例题讲解:解:根据题意,每年销售量比上一年增加的百分比相同,所以每年的销售量组成一个等比数列设为{an}课堂小结:1、等比数列前n项和公式;2、公式的推导方法—错位相减法
1.理解并掌握等比数列前n项和公式及
其推导过程.
2.能够应用前n项和公式解决等比数列
有关问题.复习引入1. 等比数列的定义:2. 等比数列通项公式:: 故事回顾讲授新课问题2:棋盘上的小麦一共有多少?问题1:棋盘上的麦粒构成什么数列? 2S64= 2+22+23+···+263+264 ② 错位相减法反思: ①式两边为什么要乘以2 ?由②-①可得:
S64 =264-1 如果1000粒麦粒重为40克,那么这些麦粒的总质量就是7300多亿吨.而全世界小麦的年产量约为6亿吨,就是说全世界都要1000多年才能生产这么多小麦,国王无论如何不能兑现自己的承诺. 探究1:= 18446744073709551615 类比探究:等比数列前n项和公式推导1①②①- ②得:正确结论:应分q=1和q ≠1讨论探究结果:探究结果:拓展探究:等比数列前n项和公式推导2理解强化小结:公式应用要明确“基本量a1、n、q”XXX例题讲解:习题讲解:拓展练习:46536例2. 某商场第一年销售计算机5000台,如果平均每年的售量比上一年增加10%,那么从第一年起,约几年内可使总销售量达到30000台(保留到个位 lg1.6=0.2,lg1.1=0.041)?例题讲解:解:根据题意,每年销售量比上一年增加的百分比相同,所以每年的销售量组成一个等比数列设为{an}课堂小结:1、等比数列前n项和公式;2、公式的推导方法—错位相减法
