人教版数学必修5 1.1.1 正弦定理(共17张ppt)
文档属性
| 名称 | 人教版数学必修5 1.1.1 正弦定理(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-13 16:34:52 | ||
图片预览






文档简介
课件17张PPT。 1.1.1正弦定理
第一章 解三角形1.1 正弦定理和余弦定理 学习目标:1.通过对任意三角形边长和角度关系的探索,掌握正弦定理的内容及其证明方法;
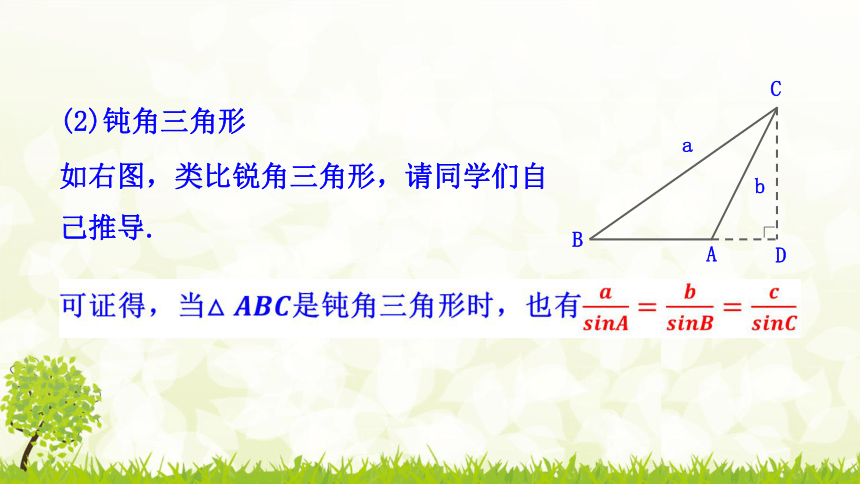
2.会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题. 新课导入:思考: 角C的大小与它的对边AB的长度之间有怎样的数量关系?显然,边AB的长度随着其对角 C 的增大而增大.能否用一个等式把这种关系精确地表示出来? BCA 课堂探究:探究一 正弦定理在初中,我们已学过如何解直角三角形,下面就首先来探讨直角三角形中,角与边的等式关系.思考:对于任意的三角形,以上关系式是否仍然成立?(1)锐角三角形(2)钝角三角形如右图,类比锐角三角形,请同学们自己推导.探究二 还有其他方法推导吗?因为涉及边长问题,从而可以考虑用向量来研究此问题.外接圆法???正弦定理: 在一个三角形中,各边和它所对角的正弦的比相等,即注意:(1)正弦定理指出了任意三角形中三条边与对应角的正弦之间的一个关系式.由正弦函数在区间上的单调性可知,正弦定理非常好地描述了任意三角形中边与角的一种数量关系.探究三 正弦定理的基本作用是什么?二.解三角形1.一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.2.已知三角形的几个元素,求其他元素的过程叫做解三角形.例1:在△ABC中,已知A=45°,B=75°,a=30cm,解三角形.
解:C=180°-45°-75°=60°
练习1:在△ABC中,A=60°,B=45°,c=20,解三角形解:C=180°-60°-45°=75°例2练习2:在△ABC中,已知a= ,b= ,A=45°,解三角形.课堂训练1.在△ABC中,已知c=10,A=45o,C=30o,则a=_____;
2.在△ABC中,已知a=8,B=60o,C=75o,则b=_____课堂小结一:正弦定理:其中,R是△ABC的外接圆的半径二:可以用正弦定理解决的三角问题:※题型一:知两角及一边,求其它的边和角
题型二:知两边及其中一边对角,求其他边和角
第一章 解三角形1.1 正弦定理和余弦定理 学习目标:1.通过对任意三角形边长和角度关系的探索,掌握正弦定理的内容及其证明方法;
2.会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题. 新课导入:思考: 角C的大小与它的对边AB的长度之间有怎样的数量关系?显然,边AB的长度随着其对角 C 的增大而增大.能否用一个等式把这种关系精确地表示出来? BCA 课堂探究:探究一 正弦定理在初中,我们已学过如何解直角三角形,下面就首先来探讨直角三角形中,角与边的等式关系.思考:对于任意的三角形,以上关系式是否仍然成立?(1)锐角三角形(2)钝角三角形如右图,类比锐角三角形,请同学们自己推导.探究二 还有其他方法推导吗?因为涉及边长问题,从而可以考虑用向量来研究此问题.外接圆法???正弦定理: 在一个三角形中,各边和它所对角的正弦的比相等,即注意:(1)正弦定理指出了任意三角形中三条边与对应角的正弦之间的一个关系式.由正弦函数在区间上的单调性可知,正弦定理非常好地描述了任意三角形中边与角的一种数量关系.探究三 正弦定理的基本作用是什么?二.解三角形1.一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.2.已知三角形的几个元素,求其他元素的过程叫做解三角形.例1:在△ABC中,已知A=45°,B=75°,a=30cm,解三角形.
解:C=180°-45°-75°=60°
练习1:在△ABC中,A=60°,B=45°,c=20,解三角形解:C=180°-60°-45°=75°例2练习2:在△ABC中,已知a= ,b= ,A=45°,解三角形.课堂训练1.在△ABC中,已知c=10,A=45o,C=30o,则a=_____;
2.在△ABC中,已知a=8,B=60o,C=75o,则b=_____课堂小结一:正弦定理:其中,R是△ABC的外接圆的半径二:可以用正弦定理解决的三角问题:※题型一:知两角及一边,求其它的边和角
题型二:知两边及其中一边对角,求其他边和角
