高中数学必修三知识讲解,巩固练习(复习补习,期末复习资料):21《概率》全章复习与巩固
文档属性
| 名称 | 高中数学必修三知识讲解,巩固练习(复习补习,期末复习资料):21《概率》全章复习与巩固 |
|
|
| 格式 | zip | ||
| 文件大小 | 482.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 11:03:38 | ||
图片预览





文档简介
《概率》全章复习与巩固
【学习目标】
1.了解随机事件发生的不确定性和频率的稳定性,了解概率的意义以及频率与概率的区别.
2.会用互斥事件的概率加法公式求互斥事件的概率.
3.理解古典概型及其概率计算公式,会计算一些随机事件发生的概率.
4.了解随机数的意义,能运用模拟方法估计概率,初步体会几何概型的意义.
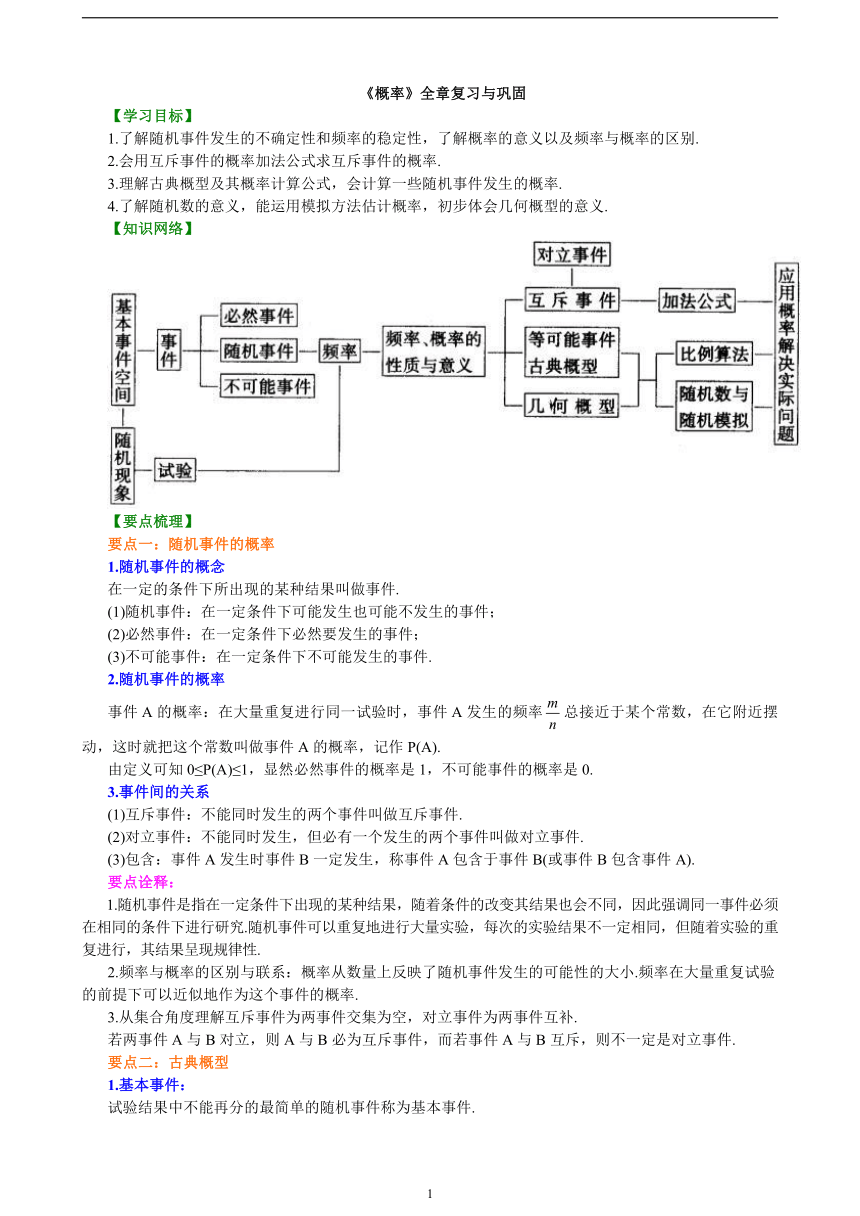
【知识网络】
【要点梳理】
要点一:随机事件的概率
1.随机事件的概念
在一定的条件下所出现的某种结果叫做事件.
(1)随机事件:在一定条件下可能发生也可能不发生的事件;
(2)必然事件:在一定条件下必然要发生的事件;
(3)不可能事件:在一定条件下不可能发生的事件.
2.随机事件的概率
事件A的概率:在大量重复进行同一试验时,事件A发生的频率总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A).
由定义可知0≤P(A)≤1,显然必然事件的概率是1,不可能事件的概率是0.
3.事件间的关系
(1)互斥事件:不能同时发生的两个事件叫做互斥事件.
(2)对立事件:不能同时发生,但必有一个发生的两个事件叫做对立事件.
(3)包含:事件A发生时事件B一定发生,称事件A包含于事件B(或事件B包含事件A).
要点诠释:
1.随机事件是指在一定条件下出现的某种结果,随着条件的改变其结果也会不同,因此强调同一事件必须在相同的条件下进行研究.随机事件可以重复地进行大量实验,每次的实验结果不一定相同,但随着实验的重复进行,其结果呈现规律性.
2.频率与概率的区别与联系:概率从数量上反映了随机事件发生的可能性的大小.频率在大量重复试验的前提下可以近似地作为这个事件的概率.
3.从集合角度理解互斥事件为两事件交集为空,对立事件为两事件互补.
若两事件A与B对立,则A与B必为互斥事件,而若事件A与B互斥,则不一定是对立事件.
要点二:古典概型
1.基本事件:
试验结果中不能再分的最简单的随机事件称为基本事件.
基本事件的特点:
(1)每个基本事件的发生都是等可能的.
(2)因为试验结果是有限个,所以基本事件也只有有限个.
(3)任意两个基本事件都是互斥的,一次试验只能出现一个结果,即产生一个基本事件.
(4)基本事件是试验中不能再分的最简单的随机事件,其他事件都可以用基本事件的和的形式来表示.
2.古典概型的定义:
(1)有限性:试验中所有可能出现的基本事件只有有限个;
(2)等可能性:每个基本事件出现的可能性相等;
我们把具有上述两个特点的概率模型称为古典概率模型,简称古典概型.
3.计算古典概型的概率的基本步骤为:
(1)计算所求事件A所包含的基本事件个数m;
(2)计算基本事件的总数n;
(3)应用公式计算概率.
4.古典概型的概率公式:
.应用公式的关键在于准确计算事件所包含的基本事件的个数和基本事件的总数.
要点诠释:
古典概型的判断:如果一个概率模型是古典概型,则其必须满足以上两个条件,有一条不满足则必不是古典概型.如“掷均匀的骰子和硬币”问题满足以上两个条件,所以是古典概型问题;若骰子或硬币不均匀,则每个基本事件出现的可能性不同,从而不是古典概型问题;“在线段AB上任取一点C,求AC>BC的概率”问题,因为基本事件为无限个,所以也不是古典概型问题.
要点三:几何概型
1.几何概型的概念:
对于一个随机试验,我们将每个基本事件理解为从某个特定的几何区域内随机地取一点,该区域中每一点被取到的机会都一样;而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点.这里的区域可以是线段,平面图形,立体图形等.用这种方法处理随机试验,称为几何概型.
2.几何概型的基本特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个;
(2)每个基本事件出现的可能性相等.
3.几何概型的概率:
一般地,在几何区域中随机地取一点,记事件"该点落在其内部一个区域内"为事件,则事件发生的概率.
说明:(1)的测度不为;
(2)其中"测度"的意义依确定,当分别是线段,平面图形,立体图形时,相应的"测度"分别是长度,面积和体积;
(3)区域为"开区域";
(4)区域内随机取点是指:该点落在区域内任何一处都是等可能的,落在任何部分的可能性大小只与该部分的测度成正比而与其形状位置无关.
要点诠释:
几种常见的几何概型
(1)设线段是线段L的一部分,向线段L上任投一点,若落在线段上的点数与线段的长度成正比,而与线段在线段L上的相对位置无关,则点落在线段上的概率为:
P=的长度/L的长度
(2)设平面区域g是平面区域G的一部分,向区域G上任投一点,若落在区域g上的点数与区域g的面积成正比,而与区域g在区域G上的相对位置无关,则点落在区域g上概率为:
P=g的面积/G的面积
(3)设空间区域上v是空间区域V的一部分,向区域V上任投一点,若落在区域v上的点数与区域v的体积成正比,而与区域v在区域V上的相对位置无关,则点落在区域v上的概率为:
P=v的体积/V的体积
要点四:随机数的产生
1.随机数的概念
随机数是在一定范围内随机产生的数,并且得到这个范围内任何一个数的机会是均等的.它可以帮助我们模拟随机试验,特别是一些成本高、时间长的试验,用随机模拟的方法可以起到降低成本,缩短时间的作用.
2.随机数的产生方法:
一般用试验的方法,如把数字标在小球上,搅拌均匀,用统计中的抽签法等抽样方法,可以产生某个范围内的随机数.在计算器或计算机中可以应用随机函数产生某个范围的伪随机数,当作随机数来应用.
3.随机模拟法(蒙特卡罗法):
用计算机或计算器模拟试验的方法,具体步骤如下:
(1)用计算器或计算机产生某个范围内的随机数,并赋予每个随机数一定的意义;
(2)统计代表某意义的随机数的个数M和总的随机数个数N;
(3)计算频率作为所求概率的近似值.
要点诠释:
1.对于抽签法等抽样方法试验,如果亲手做大量重复试验的话,花费的时间太多,因此利用计算机或计算器做随机模拟试验可以大大节省时间.
2.随机函数RANDBETWEEN(a,b)产生从整数a到整数b的取整数值的随机数.
3. 随机数具有广泛的应用,可以帮助我们安排和模拟一些试验,这样可以代替我们自己做大量重复试验,比如现在很多城市的重要考试采用产生随机数的方法把考生分配到各个考场中.
4.在区间[a,b]上的均匀随机数与整数值随机数的共同点都是等可能取值,不同点是均匀随机数可以取区间内的任意一个实数,整数值随机数只取区间内的整数.
5.利用几何概型的概率公式,结合随机模拟试验,可以解决求概率、面积、参数值等一系列问题,体现了数学知识的应用价值.
6.用随机模拟试验不规则图形的面积的基本思想是,构造一个包含这个图形的规则图形作为参照,通过计算机产生某区间内的均匀随机数,再利用两个图形的面积之比近似等于分别落在这两个图形区域内的均匀随机点的个数之比来解决.
7.利用计算机和线性变换Y=X*(b-a)+a,可以产生任意区间[a,b]上的均匀随机数.
要点五:求解概率问题应当注意的问题
1.求解概率问题应首先分清是哪类概率问题,针对不同的概型灵活选择相应的方法及公式.
2.求解概率的应用问题一般可分为三步:①用字母恰当地表示相关事件;②明确事件之间的关系,如互斥、对立、独立等;③运用正确的计算公式.
3.对于稍微复杂的事件的概率求解时,通常有两种方法,一是将所求事件转化为彼此互斥的事件的和,二是先求出此事件的对立事件(适用于“至多”“至少”型的事件概率)的概率.
4.几何概型问题时常借助图形的直观帮助分析.
【典型例题】
要点一:随机事件与概率
例1.某射手在相同条件下进行射击,结果如下:
(1)问该射手射击一次,击中靶心的概率约是多少?
(2)假设该射手射击了300次,估计击中靶心的次数是多少?
【思路点拨】弄清频率和概率的含义及它们之间的关系是解题的关键.
【解析】(1)由表可知概率约为0.9;
(2)估计击中靶心的次数为300×0.9=270(次).
【总结升华】本题中利用概率知识估计击中靶心的次数是一种非常科学的决策方法.
举一反三:
【变式1】若在同等条件下进行次重复试验得到某个事件A发生的频率,则随着的逐渐增大,有( )
A.与某个常数相等
B.与某个常数的差逐渐减小
C.与某个常数的差的绝对值逐渐减小
D.与某个常数的附近摆动并趋于稳定
【答案】本题选D,根据概率的定义.
要点二:互斥事件与对立事件
例2.经统计,在某储蓄所一个营业窗口等候的人数及相应概率如下:
(1)至多2人排队等候的概率是多少?
(2)至少3人排队等候的概率是多少?
【思路点拨】利用互斥事件概率加法公式计算.
【解析】记“等候的人数为0”为事件A,“1人等候”为事件B,“2人等候”为事件C,“3人等候”为事件D,“4人等候”为事件E,“5人及5人以上等候”为事件F,则易知A、B、C、D、E、F互斥.
(1)记“至多2人排队等候”为事件G,则G=A∪B∪C,
∴ P(G)=P(A+B+C)=P(A)+P(B)+P(C)
=0.1+0.16+0.3=0.56.
(2)记“至少3人排队等候”为事件H,则H=D∪E∪F,
∴ P(H)=P(D+E+F)=P(D)+P(E)+P(F)
=0.3+0.1+0.04=0.44.
【总结升华】第(2)问也可以这样解:因为G与H是对立事件,所以P(H)=1-P(G)=1-0.56=0.44.
举一反三:
【变式1】某地区的年降水量在下列范围内的概率如下表所示:
年降水量
(单位:mm)
概率
0.12
0.25
0.16
0.14
(1)求年降水量在内的概率;(2)求年降水量在内的概率.
【答案】(1)(2)
【解析】(1)记这个地区的年降水量在、、、范围内分别为事件,这4个事件是彼此互斥的,根据互斥事件的概率加法公式,年降水量在范围内的概率是
∴年降水量在范围内的概率是.
(2)年降水量在范围内的概率是
∴年降水量在范围内的概率是.
要点三:古典概型
例3.5张奖券中有2张是中奖的,首先由甲抽一张,然后由乙抽一张,求:
(1)甲中奖的概率P(A);
(2)甲、乙都中奖的概率P(B);
(3)只有乙中奖的概率P(C);
(4)乙中奖的概率P(D).
【思路点拨】先确定事件总数,再确定四个事件中包含的基本事件个数,用古典概率公式求解.
【解析】甲、乙两人按顺序各抽一张,5张奖券分别为A1,A2,B1,B2,B3,其中A1,A2为中奖券,则基本事件为(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,A1),(A2,B1),(A2,B2),(A2,B3),(B1,A1),(B1,A2),(B1,B2),(B1,B3),(B2,A1),(B2,A2),(B2,B1),(B2,B3),(B3,A1),(B3,A2),(B3,B1),(B3,B2),共20种.
(1)若“甲中奖”,则有(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,A1),(A2,B1),(A2,B2),(A2,B3),共8种,故P(A).
(2)甲、乙都中奖含有的基本事件有(A1,A2),(A2,A1),共2种,所以P(B)=.
(3)“只有乙中奖”的基本事件有(B1,A1),(B2,A1),(B3,A1),(B1,A2),(B2,A2),(B3,A2),共6种,故.
(4)“乙中奖”的基本事件有(A2,A1),(B1,A1),(B2,A1),(B3,A1),(Al,A2),(B1,A2),(B2,A2),(B3,A2),共8种,故.
【总结升华】
1、利用古典概型的计算公式时应注意两点:
(1)所有的基本事件必须是互斥的;
(2)m为事件A所包含的基本事件数,求m值时,要做到不重不漏.
2、古典概型解题步骤:
(1)阅读题目,搜集信息;
(2)判断是否是等可能事件,并用字母表示事件;
(3)求出基本事件总数和事件所包含的结果数;
(4)用公式求出概率并下结论.
举一反三:
【变式1】
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相邻整数的概率;
(Ⅱ)求取出的两个球上标号之和能被3整除的概率.
【答案】(Ⅰ) (Ⅱ)
【解析】设从甲、乙两个盒子中各取1个球,其数字分别为,用表示抽取结果,则所有可能有,,,,,,,,,,,,,,,,共16种.
(Ⅰ)所取两个小球上的数字为相邻整数的结果有, , ,, , ,共6种. 故所求概率.
(Ⅱ)所取两个球上的数字和能被3整除的结果有, , , , ,共5种. 故所求概率为.
【变式2】(2018 兰州模拟)一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同,随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
(注:若三个数a,b,c满足a≤b≤c,则称b为这三个数的中位数)
【答案】(1);(2)
【解析】(1)由题意,(a,b,c)所有的可能为:
(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),
(1,3,1),(1,3,2),(1,3,3),(2,1,1),(2,1,2),(2,1,3),
(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),
(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),
(3,3,1),(3,3,2),(3,3,3),共27种.
设“抽取的卡片上的数字满足a+b=c”为事件A,则事件A包括(1,1,2),(1,2,3),(2,1,3),共3种,
所以.
因此,“抽取的卡片上的数字满足a+b=c”的概率为.
(2)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,则事件包括(1,1,1,),(2,2,2),(3,3,3),共3种.
所以.
因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为.
要点四:几何概型
例4.(2018 福建安溪县模拟)某旅游公司为甲,乙两个旅游团提供三条不同的旅游线路,每个旅游团可任选其中一条旅游线路.
(1)求甲、乙两个旅游团所选旅游线路相同的概率.
(2)某天上午9时至10时,甲,乙两个旅游团都到同一个著名景点游览,20分钟后游览结束即离去.求两个旅游团在该著名景点相遇的概率.
【思路点拨】(1)列举法写出所有基本事件,从中找出符合条件的基本事件,利用基本事件个数比求概率;
(2)用平面区域分布表示实验及满足条件的实验,利用面积比求概率.
【答案】(1);(2)
【解析】(1)用1,2,3表示三条不同的旅游线路,事件用(甲,乙)表示.
基本事件:有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)共9个.
记“甲,乙两个旅游团所选旅游线路相同”为事件有(1,1),(2,2),(3,3)3个,
∴;
(2)设甲,乙两个旅游团到达著名景点的时刻分别为x,y,
则0≤x≤60,0≤y≤60,事件对应区域如图:
两个旅游团在该著名景点相遇,则满足|x-y|≤20,事件对应的区域为图中阴影部分,
∴两个旅游团在著名景点相遇的概率.
【总结升华】本题考查了古典概型的概率计算,考查了几何概型的概率计算,熟练掌握两种概型的特征及管理计算方法是解题的关键.
举一反三:
【变式1】在0~1之间随机选择两个数,这两个数对应的点把长度为1的线段分成了三条线段,试求这三条线段能构成三角形的概率.
【解析】设三条线段的长度分别为x,y,1-x-y,
则
即
在平面上建立如图所示的平面直角坐标系,直线x=0,y=0,y=-x+1围成如图所示三角形区域G(不包括边界),每一对(x,y)对应着G内的点(x,y),由题意知,每个试验结果出现的可能性相等,因此,试验属于几何概型.三条线段能构成三角形,当且仅当
即
因此图中的阴影区域g就表示“三条线段能构成三角形”,容易求得g的面积为,G的面积为,则P(这三条线段能构成三角形).
【变式2】已知关于x的二次函数.
(1)设集合P={-1,1,2,3,4,5}和Q={-2,-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数在区间[1,+∞)上是增函数的概率:
(2)设点(a,b)是区域内的随机点,求函数在区间[1,+∞)上是增函数的概率.
【思路点拨】(1)用古典概型的概率公式计算.(2)属于几何概型问题,用几何概型的知识求解.
【解析】(1)∵ 函数的图像的对称轴为,要使函数在区间[1,+∞)上为增函数,当且仅当a>0且,即2b≤a,a>0.
若a=1,则b=-2,-1;
若a=2,则b=-2,-1,1;
若a=3,则b=-2,-1,1;
若a=4,则b=-2,-1,1,2;
若a=5,则b=-2,-1,1,2.
∴ 满足条件的事件包含事件的个数是2+3+3+4+4=16.
∴ 所求事件的概率为.
(2)由(1)知,当且仅当2b≤a且a>0时,函数在区间[1,+∞)上为增函数,依条件可知试验的全部结果所构成的区域为构成所求事件的区域为如图所示阴影部分.
由得交点坐标为,
∴ 所求事件的概率为.
【总结升华】几何概型的概率问题关键是数形结合,将问题转化成与长度、角度、面积、体积等相关的类型解决.
【巩固练习】
1.一个射手进行射击,记事件E1:“脱靶”,E2:“中靶”,E3:“中靶环数大于4”,E4:“中靶环数不小于5”,则在上述事件中,互斥而不对立的事件共有( )
A.1对 B.2对 C.3对 D.4对
2.某校学生毕业后有回家待业,上大学和补习的三种方式,现取一个样本调查结果如图所示,若该校每一个学生上大学的概率为,则每个学生补习的概率为( )
A. B. C. D.
3.从一批羽毛球产品中任取一个,其质量小于4.8 g的概率为0.3,质量小于4.85g的概率为0.32,那么质量在[4.8,4.85)(g)范围内的概率是( )
A.0.62 B.0.38 C.0.02 D.0.68
4.先后抛掷硬币三次,则至少一次正面朝上的概率是( )
A. B. C. D.
5.(2018 江西上饶校级一模)从标有1,2,3,4,5,6的6张纸片中任取2张,那么这2张纸片数字之积为6的概率是( )
A. B. C. D.
6.如图所示,在两个圆盘中,指针落在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是( )
A. B. C. D.
7.一条河上有一个渡口,每隔一小时有一趟渡船,河的上游还有一座桥,某人到这个渡口等候渡船,他准备等候20分钟,如果20分钟渡船不到,他就要绕到上游从桥上过河,则他乘船过河的概率为( )
A. B. C. D.
8.任取一个三位数的正整数N,则log2N为一个正整数的概率是( )
A. B. C. D.
9.广告法对插广告时间有规定,某人对某台的电视节目作了长期的统计后得到结论,他任意时间打开电视看该台节目,看不到广告的概率约为,那么该台每小时约有_______分钟插播广告.
10.(2018 江苏泰州一模)袋子里有两个不同的红球和两个不同的白球,从中任取两个球,则这两个球颜色相同的概率为________.
11.如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积为________.
12.2盒中有1个红球和9个白球,它们除颜色不同外,其他方面没有什么差别.现由10人依次摸出1个球,设第1个人摸出的1个球是红球的概率为P1,…,第8个人摸出红球的概率是P8,则________.
13.对某电视机厂生产的电视机进行抽样检测的数据如下:
(1)计算表中优等品的各个频率.
(2)该厂生产的电视机优等品的概率约是多少?
14.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x,第二次出现的点数为y.
(1)求事件“x+y≤3”的概率;
(2)求事件“|x-y|=2”的概率.
15.(2018春 江苏无锡期末)如图,四边形ABCD由不等式组所围成的平面区域,动直线y=x+b与线段BC、CD分别交于M、N.
(1)现向四边形ABCD内丢一粒豆子,求豆子落在三角形MNC内的概率;
(2)若将横、纵坐标均为整数的点称为格点,记事件A为:在四边形ABCD内取一格点恰好落在三角形MNC(不含边界)内,若,求b的取值范围.
16.某初级中学共有学生2 000名,各年级男、女生人数如下表:
已知在全校学生中随机抽取1名,抽到八年级女生的概率是0.19.
(1)求x的值.
(2)现用分层抽样的方法在全校抽取48名学生,问应在九年级抽取多少名?
(3)已知y≥245,z≥245,求九年级中女生比男生多的概率.
【答案与解析】
参考答案
1.【答案】B
【解析】E1与E3,E1与E4均为互斥而不对立的事件.
2.【答案】C
【解析】设某校毕业生的人数为x人,则每个学生上大学的概率为,所以x=100,则补习生的人数为12人,所以每个学生补习的概率为.
3.【答案】C
【解析】记事件A、B分别为“质量小于4.8 g”与“质量在[4.8,4.85)(g)”,又记事件C为“质量小于4.85 g”,则C=A+B,且A与B互斥,所以P(C)=P(A)+P(B),即0.32=0.3+P(A),解得P(A)=0.02.
4. 【答案】D
【解析】至少一次正面朝上的对立事件的概率为
5.【答案】C.
【解析】从标有1,2,3,4,5,6的6张纸片中任取2张,不同的取法种数是12、13、14、15、16、23、24、25、26、34、35、36、45、46、56共15种;
其中这2张纸片数字之积为6的取法种数是23、16;
∴对应的概率是.
故选:C.
6.【答案】A
【解析】记a,b分别为两个指针所落在区域中的数,则所有可能结果(a,b)有(1,1),(1,2),(1,3).(1,7),(1,8),(1,9),(2,1),…,(7,8),(7,9),即共有6×6=36(个),而(a,b)中的a,b均为奇数有(1,1),(1,3),(1,7),(1,9),(3,1),(3,3),(3,7),(3,9),(5,1),(5,3),(5,7),(5,9),(7,1),(7,3),(7,7),(7,9),共4×4=16(个),所以由古典概型的概率的计算公式得所求概率为.
7.【答案】C
【解析】考虑一趟渡船离开到下一趟渡船到达之间的1个小时为基本事件的全部,由几何概型可以求得,此人乘船过河的概率为.
8.【答案】B
【解析】因为三位数的正整数N共有900个,其中为一个正整数的N只有:27,28,29三个,所以所求的概率为.
9.【答案】6
【解析】某人打开电视看该台节目,看到广告的概率约为,所以该台每小时约有60×6(分钟)插播广告.
10.【答案】
【解析】从中任取两个球共有红1红2,红1白1,红1白2,红2白1,红2白1,红2白2,白1白2,共6种取法,其中颜相同只有2种,
故从中任取两个球,则这两个球颜色相同的概率;
故答案为:.
11.【答案】
【解析】由几何概型的计算公式知,,则.
12.【答案】
【解析】虽然摸球的顺序有先后,但只需不让后摸的人知道先摸者摸出的结果,那么各个摸球者摸到红球的概率都是相等的,并不因摸球的顺序不同而影响其公平性.
13.【解析】(1)由频率公式及题意可计算出优等品的频率依次为0.8,0.92,0.96,0.95,0.956,0.954.
(2)由(1)知,计算出的优等品的频率虽然各不相同,但都是在常数0.95附近摆动,因此,可估计该厂的电视机优等品的概率约是0.95.
14.【解析】设(x,y)表示一个基本事件,则掷两次骰子包括:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…,(6,5),(6,6),共36个基本事件.
(1)用A表示事件“x+y≤3”,
则A的结果有(1,1),(1,2),(2,1),共3个基本事件,
∵ P(A)=.
答:事件“x+y≤3”的概率为.
(2)用B表示事件“|x-y|=2”,
则B的结果有(1,3),(2,4),(3,5),(4,6),(6,4),(5,3),(4,2),(3,1),共8个基本事件,
∴ P(B)=.
答:事件“|x-y|=2”的概率为.
15.【答案】(1);(2)-2<b≤-1.
【解析】(1)b=―3时,直线为y=x―3,此时N(3,0),M(0,―3),
∴,
∵,
∴豆子落在三角形MNC内的概率为;
(2)四边形ABCD内的格点共有25个,落在三角形MNC(不含边界)内的格点有6个,
∴-2<b≤-1.
16.【解析】(1)∵ ,∴ x=380.
(2)九年级人数为y+z=2000-(373+377+380+370)=500,
现用分层抽样的方法在全校抽取48名学生,应在九年级抽取的人数为:名.
(3)设九年级女生比男生多的事件为A,九年级女生、男生数记为(y,z);
由(2)知y+z=500,且y,z∈N,基本事件有:
(245,255)、(246,254)、(247,253)、…、(255,245),共11个,
事件A包含的基本事件有:(251,249)、(252,248)、(253,247)、(254,246)、(255,245),共5个,∴ .
【学习目标】
1.了解随机事件发生的不确定性和频率的稳定性,了解概率的意义以及频率与概率的区别.
2.会用互斥事件的概率加法公式求互斥事件的概率.
3.理解古典概型及其概率计算公式,会计算一些随机事件发生的概率.
4.了解随机数的意义,能运用模拟方法估计概率,初步体会几何概型的意义.
【知识网络】
【要点梳理】
要点一:随机事件的概率
1.随机事件的概念
在一定的条件下所出现的某种结果叫做事件.
(1)随机事件:在一定条件下可能发生也可能不发生的事件;
(2)必然事件:在一定条件下必然要发生的事件;
(3)不可能事件:在一定条件下不可能发生的事件.
2.随机事件的概率
事件A的概率:在大量重复进行同一试验时,事件A发生的频率总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A).
由定义可知0≤P(A)≤1,显然必然事件的概率是1,不可能事件的概率是0.
3.事件间的关系
(1)互斥事件:不能同时发生的两个事件叫做互斥事件.
(2)对立事件:不能同时发生,但必有一个发生的两个事件叫做对立事件.
(3)包含:事件A发生时事件B一定发生,称事件A包含于事件B(或事件B包含事件A).
要点诠释:
1.随机事件是指在一定条件下出现的某种结果,随着条件的改变其结果也会不同,因此强调同一事件必须在相同的条件下进行研究.随机事件可以重复地进行大量实验,每次的实验结果不一定相同,但随着实验的重复进行,其结果呈现规律性.
2.频率与概率的区别与联系:概率从数量上反映了随机事件发生的可能性的大小.频率在大量重复试验的前提下可以近似地作为这个事件的概率.
3.从集合角度理解互斥事件为两事件交集为空,对立事件为两事件互补.
若两事件A与B对立,则A与B必为互斥事件,而若事件A与B互斥,则不一定是对立事件.
要点二:古典概型
1.基本事件:
试验结果中不能再分的最简单的随机事件称为基本事件.
基本事件的特点:
(1)每个基本事件的发生都是等可能的.
(2)因为试验结果是有限个,所以基本事件也只有有限个.
(3)任意两个基本事件都是互斥的,一次试验只能出现一个结果,即产生一个基本事件.
(4)基本事件是试验中不能再分的最简单的随机事件,其他事件都可以用基本事件的和的形式来表示.
2.古典概型的定义:
(1)有限性:试验中所有可能出现的基本事件只有有限个;
(2)等可能性:每个基本事件出现的可能性相等;
我们把具有上述两个特点的概率模型称为古典概率模型,简称古典概型.
3.计算古典概型的概率的基本步骤为:
(1)计算所求事件A所包含的基本事件个数m;
(2)计算基本事件的总数n;
(3)应用公式计算概率.
4.古典概型的概率公式:
.应用公式的关键在于准确计算事件所包含的基本事件的个数和基本事件的总数.
要点诠释:
古典概型的判断:如果一个概率模型是古典概型,则其必须满足以上两个条件,有一条不满足则必不是古典概型.如“掷均匀的骰子和硬币”问题满足以上两个条件,所以是古典概型问题;若骰子或硬币不均匀,则每个基本事件出现的可能性不同,从而不是古典概型问题;“在线段AB上任取一点C,求AC>BC的概率”问题,因为基本事件为无限个,所以也不是古典概型问题.
要点三:几何概型
1.几何概型的概念:
对于一个随机试验,我们将每个基本事件理解为从某个特定的几何区域内随机地取一点,该区域中每一点被取到的机会都一样;而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点.这里的区域可以是线段,平面图形,立体图形等.用这种方法处理随机试验,称为几何概型.
2.几何概型的基本特点:
(1)试验中所有可能出现的结果(基本事件)有无限多个;
(2)每个基本事件出现的可能性相等.
3.几何概型的概率:
一般地,在几何区域中随机地取一点,记事件"该点落在其内部一个区域内"为事件,则事件发生的概率.
说明:(1)的测度不为;
(2)其中"测度"的意义依确定,当分别是线段,平面图形,立体图形时,相应的"测度"分别是长度,面积和体积;
(3)区域为"开区域";
(4)区域内随机取点是指:该点落在区域内任何一处都是等可能的,落在任何部分的可能性大小只与该部分的测度成正比而与其形状位置无关.
要点诠释:
几种常见的几何概型
(1)设线段是线段L的一部分,向线段L上任投一点,若落在线段上的点数与线段的长度成正比,而与线段在线段L上的相对位置无关,则点落在线段上的概率为:
P=的长度/L的长度
(2)设平面区域g是平面区域G的一部分,向区域G上任投一点,若落在区域g上的点数与区域g的面积成正比,而与区域g在区域G上的相对位置无关,则点落在区域g上概率为:
P=g的面积/G的面积
(3)设空间区域上v是空间区域V的一部分,向区域V上任投一点,若落在区域v上的点数与区域v的体积成正比,而与区域v在区域V上的相对位置无关,则点落在区域v上的概率为:
P=v的体积/V的体积
要点四:随机数的产生
1.随机数的概念
随机数是在一定范围内随机产生的数,并且得到这个范围内任何一个数的机会是均等的.它可以帮助我们模拟随机试验,特别是一些成本高、时间长的试验,用随机模拟的方法可以起到降低成本,缩短时间的作用.
2.随机数的产生方法:
一般用试验的方法,如把数字标在小球上,搅拌均匀,用统计中的抽签法等抽样方法,可以产生某个范围内的随机数.在计算器或计算机中可以应用随机函数产生某个范围的伪随机数,当作随机数来应用.
3.随机模拟法(蒙特卡罗法):
用计算机或计算器模拟试验的方法,具体步骤如下:
(1)用计算器或计算机产生某个范围内的随机数,并赋予每个随机数一定的意义;
(2)统计代表某意义的随机数的个数M和总的随机数个数N;
(3)计算频率作为所求概率的近似值.
要点诠释:
1.对于抽签法等抽样方法试验,如果亲手做大量重复试验的话,花费的时间太多,因此利用计算机或计算器做随机模拟试验可以大大节省时间.
2.随机函数RANDBETWEEN(a,b)产生从整数a到整数b的取整数值的随机数.
3. 随机数具有广泛的应用,可以帮助我们安排和模拟一些试验,这样可以代替我们自己做大量重复试验,比如现在很多城市的重要考试采用产生随机数的方法把考生分配到各个考场中.
4.在区间[a,b]上的均匀随机数与整数值随机数的共同点都是等可能取值,不同点是均匀随机数可以取区间内的任意一个实数,整数值随机数只取区间内的整数.
5.利用几何概型的概率公式,结合随机模拟试验,可以解决求概率、面积、参数值等一系列问题,体现了数学知识的应用价值.
6.用随机模拟试验不规则图形的面积的基本思想是,构造一个包含这个图形的规则图形作为参照,通过计算机产生某区间内的均匀随机数,再利用两个图形的面积之比近似等于分别落在这两个图形区域内的均匀随机点的个数之比来解决.
7.利用计算机和线性变换Y=X*(b-a)+a,可以产生任意区间[a,b]上的均匀随机数.
要点五:求解概率问题应当注意的问题
1.求解概率问题应首先分清是哪类概率问题,针对不同的概型灵活选择相应的方法及公式.
2.求解概率的应用问题一般可分为三步:①用字母恰当地表示相关事件;②明确事件之间的关系,如互斥、对立、独立等;③运用正确的计算公式.
3.对于稍微复杂的事件的概率求解时,通常有两种方法,一是将所求事件转化为彼此互斥的事件的和,二是先求出此事件的对立事件(适用于“至多”“至少”型的事件概率)的概率.
4.几何概型问题时常借助图形的直观帮助分析.
【典型例题】
要点一:随机事件与概率
例1.某射手在相同条件下进行射击,结果如下:
(1)问该射手射击一次,击中靶心的概率约是多少?
(2)假设该射手射击了300次,估计击中靶心的次数是多少?
【思路点拨】弄清频率和概率的含义及它们之间的关系是解题的关键.
【解析】(1)由表可知概率约为0.9;
(2)估计击中靶心的次数为300×0.9=270(次).
【总结升华】本题中利用概率知识估计击中靶心的次数是一种非常科学的决策方法.
举一反三:
【变式1】若在同等条件下进行次重复试验得到某个事件A发生的频率,则随着的逐渐增大,有( )
A.与某个常数相等
B.与某个常数的差逐渐减小
C.与某个常数的差的绝对值逐渐减小
D.与某个常数的附近摆动并趋于稳定
【答案】本题选D,根据概率的定义.
要点二:互斥事件与对立事件
例2.经统计,在某储蓄所一个营业窗口等候的人数及相应概率如下:
(1)至多2人排队等候的概率是多少?
(2)至少3人排队等候的概率是多少?
【思路点拨】利用互斥事件概率加法公式计算.
【解析】记“等候的人数为0”为事件A,“1人等候”为事件B,“2人等候”为事件C,“3人等候”为事件D,“4人等候”为事件E,“5人及5人以上等候”为事件F,则易知A、B、C、D、E、F互斥.
(1)记“至多2人排队等候”为事件G,则G=A∪B∪C,
∴ P(G)=P(A+B+C)=P(A)+P(B)+P(C)
=0.1+0.16+0.3=0.56.
(2)记“至少3人排队等候”为事件H,则H=D∪E∪F,
∴ P(H)=P(D+E+F)=P(D)+P(E)+P(F)
=0.3+0.1+0.04=0.44.
【总结升华】第(2)问也可以这样解:因为G与H是对立事件,所以P(H)=1-P(G)=1-0.56=0.44.
举一反三:
【变式1】某地区的年降水量在下列范围内的概率如下表所示:
年降水量
(单位:mm)
概率
0.12
0.25
0.16
0.14
(1)求年降水量在内的概率;(2)求年降水量在内的概率.
【答案】(1)(2)
【解析】(1)记这个地区的年降水量在、、、范围内分别为事件,这4个事件是彼此互斥的,根据互斥事件的概率加法公式,年降水量在范围内的概率是
∴年降水量在范围内的概率是.
(2)年降水量在范围内的概率是
∴年降水量在范围内的概率是.
要点三:古典概型
例3.5张奖券中有2张是中奖的,首先由甲抽一张,然后由乙抽一张,求:
(1)甲中奖的概率P(A);
(2)甲、乙都中奖的概率P(B);
(3)只有乙中奖的概率P(C);
(4)乙中奖的概率P(D).
【思路点拨】先确定事件总数,再确定四个事件中包含的基本事件个数,用古典概率公式求解.
【解析】甲、乙两人按顺序各抽一张,5张奖券分别为A1,A2,B1,B2,B3,其中A1,A2为中奖券,则基本事件为(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,A1),(A2,B1),(A2,B2),(A2,B3),(B1,A1),(B1,A2),(B1,B2),(B1,B3),(B2,A1),(B2,A2),(B2,B1),(B2,B3),(B3,A1),(B3,A2),(B3,B1),(B3,B2),共20种.
(1)若“甲中奖”,则有(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,A1),(A2,B1),(A2,B2),(A2,B3),共8种,故P(A).
(2)甲、乙都中奖含有的基本事件有(A1,A2),(A2,A1),共2种,所以P(B)=.
(3)“只有乙中奖”的基本事件有(B1,A1),(B2,A1),(B3,A1),(B1,A2),(B2,A2),(B3,A2),共6种,故.
(4)“乙中奖”的基本事件有(A2,A1),(B1,A1),(B2,A1),(B3,A1),(Al,A2),(B1,A2),(B2,A2),(B3,A2),共8种,故.
【总结升华】
1、利用古典概型的计算公式时应注意两点:
(1)所有的基本事件必须是互斥的;
(2)m为事件A所包含的基本事件数,求m值时,要做到不重不漏.
2、古典概型解题步骤:
(1)阅读题目,搜集信息;
(2)判断是否是等可能事件,并用字母表示事件;
(3)求出基本事件总数和事件所包含的结果数;
(4)用公式求出概率并下结论.
举一反三:
【变式1】
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相邻整数的概率;
(Ⅱ)求取出的两个球上标号之和能被3整除的概率.
【答案】(Ⅰ) (Ⅱ)
【解析】设从甲、乙两个盒子中各取1个球,其数字分别为,用表示抽取结果,则所有可能有,,,,,,,,,,,,,,,,共16种.
(Ⅰ)所取两个小球上的数字为相邻整数的结果有, , ,, , ,共6种. 故所求概率.
(Ⅱ)所取两个球上的数字和能被3整除的结果有, , , , ,共5种. 故所求概率为.
【变式2】(2018 兰州模拟)一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同,随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
(注:若三个数a,b,c满足a≤b≤c,则称b为这三个数的中位数)
【答案】(1);(2)
【解析】(1)由题意,(a,b,c)所有的可能为:
(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),
(1,3,1),(1,3,2),(1,3,3),(2,1,1),(2,1,2),(2,1,3),
(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),
(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),
(3,3,1),(3,3,2),(3,3,3),共27种.
设“抽取的卡片上的数字满足a+b=c”为事件A,则事件A包括(1,1,2),(1,2,3),(2,1,3),共3种,
所以.
因此,“抽取的卡片上的数字满足a+b=c”的概率为.
(2)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,则事件包括(1,1,1,),(2,2,2),(3,3,3),共3种.
所以.
因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为.
要点四:几何概型
例4.(2018 福建安溪县模拟)某旅游公司为甲,乙两个旅游团提供三条不同的旅游线路,每个旅游团可任选其中一条旅游线路.
(1)求甲、乙两个旅游团所选旅游线路相同的概率.
(2)某天上午9时至10时,甲,乙两个旅游团都到同一个著名景点游览,20分钟后游览结束即离去.求两个旅游团在该著名景点相遇的概率.
【思路点拨】(1)列举法写出所有基本事件,从中找出符合条件的基本事件,利用基本事件个数比求概率;
(2)用平面区域分布表示实验及满足条件的实验,利用面积比求概率.
【答案】(1);(2)
【解析】(1)用1,2,3表示三条不同的旅游线路,事件用(甲,乙)表示.
基本事件:有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)共9个.
记“甲,乙两个旅游团所选旅游线路相同”为事件有(1,1),(2,2),(3,3)3个,
∴;
(2)设甲,乙两个旅游团到达著名景点的时刻分别为x,y,
则0≤x≤60,0≤y≤60,事件对应区域如图:
两个旅游团在该著名景点相遇,则满足|x-y|≤20,事件对应的区域为图中阴影部分,
∴两个旅游团在著名景点相遇的概率.
【总结升华】本题考查了古典概型的概率计算,考查了几何概型的概率计算,熟练掌握两种概型的特征及管理计算方法是解题的关键.
举一反三:
【变式1】在0~1之间随机选择两个数,这两个数对应的点把长度为1的线段分成了三条线段,试求这三条线段能构成三角形的概率.
【解析】设三条线段的长度分别为x,y,1-x-y,
则
即
在平面上建立如图所示的平面直角坐标系,直线x=0,y=0,y=-x+1围成如图所示三角形区域G(不包括边界),每一对(x,y)对应着G内的点(x,y),由题意知,每个试验结果出现的可能性相等,因此,试验属于几何概型.三条线段能构成三角形,当且仅当
即
因此图中的阴影区域g就表示“三条线段能构成三角形”,容易求得g的面积为,G的面积为,则P(这三条线段能构成三角形).
【变式2】已知关于x的二次函数.
(1)设集合P={-1,1,2,3,4,5}和Q={-2,-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数在区间[1,+∞)上是增函数的概率:
(2)设点(a,b)是区域内的随机点,求函数在区间[1,+∞)上是增函数的概率.
【思路点拨】(1)用古典概型的概率公式计算.(2)属于几何概型问题,用几何概型的知识求解.
【解析】(1)∵ 函数的图像的对称轴为,要使函数在区间[1,+∞)上为增函数,当且仅当a>0且,即2b≤a,a>0.
若a=1,则b=-2,-1;
若a=2,则b=-2,-1,1;
若a=3,则b=-2,-1,1;
若a=4,则b=-2,-1,1,2;
若a=5,则b=-2,-1,1,2.
∴ 满足条件的事件包含事件的个数是2+3+3+4+4=16.
∴ 所求事件的概率为.
(2)由(1)知,当且仅当2b≤a且a>0时,函数在区间[1,+∞)上为增函数,依条件可知试验的全部结果所构成的区域为构成所求事件的区域为如图所示阴影部分.
由得交点坐标为,
∴ 所求事件的概率为.
【总结升华】几何概型的概率问题关键是数形结合,将问题转化成与长度、角度、面积、体积等相关的类型解决.
【巩固练习】
1.一个射手进行射击,记事件E1:“脱靶”,E2:“中靶”,E3:“中靶环数大于4”,E4:“中靶环数不小于5”,则在上述事件中,互斥而不对立的事件共有( )
A.1对 B.2对 C.3对 D.4对
2.某校学生毕业后有回家待业,上大学和补习的三种方式,现取一个样本调查结果如图所示,若该校每一个学生上大学的概率为,则每个学生补习的概率为( )
A. B. C. D.
3.从一批羽毛球产品中任取一个,其质量小于4.8 g的概率为0.3,质量小于4.85g的概率为0.32,那么质量在[4.8,4.85)(g)范围内的概率是( )
A.0.62 B.0.38 C.0.02 D.0.68
4.先后抛掷硬币三次,则至少一次正面朝上的概率是( )
A. B. C. D.
5.(2018 江西上饶校级一模)从标有1,2,3,4,5,6的6张纸片中任取2张,那么这2张纸片数字之积为6的概率是( )
A. B. C. D.
6.如图所示,在两个圆盘中,指针落在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是( )
A. B. C. D.
7.一条河上有一个渡口,每隔一小时有一趟渡船,河的上游还有一座桥,某人到这个渡口等候渡船,他准备等候20分钟,如果20分钟渡船不到,他就要绕到上游从桥上过河,则他乘船过河的概率为( )
A. B. C. D.
8.任取一个三位数的正整数N,则log2N为一个正整数的概率是( )
A. B. C. D.
9.广告法对插广告时间有规定,某人对某台的电视节目作了长期的统计后得到结论,他任意时间打开电视看该台节目,看不到广告的概率约为,那么该台每小时约有_______分钟插播广告.
10.(2018 江苏泰州一模)袋子里有两个不同的红球和两个不同的白球,从中任取两个球,则这两个球颜色相同的概率为________.
11.如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积为________.
12.2盒中有1个红球和9个白球,它们除颜色不同外,其他方面没有什么差别.现由10人依次摸出1个球,设第1个人摸出的1个球是红球的概率为P1,…,第8个人摸出红球的概率是P8,则________.
13.对某电视机厂生产的电视机进行抽样检测的数据如下:
(1)计算表中优等品的各个频率.
(2)该厂生产的电视机优等品的概率约是多少?
14.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x,第二次出现的点数为y.
(1)求事件“x+y≤3”的概率;
(2)求事件“|x-y|=2”的概率.
15.(2018春 江苏无锡期末)如图,四边形ABCD由不等式组所围成的平面区域,动直线y=x+b与线段BC、CD分别交于M、N.
(1)现向四边形ABCD内丢一粒豆子,求豆子落在三角形MNC内的概率;
(2)若将横、纵坐标均为整数的点称为格点,记事件A为:在四边形ABCD内取一格点恰好落在三角形MNC(不含边界)内,若,求b的取值范围.
16.某初级中学共有学生2 000名,各年级男、女生人数如下表:
已知在全校学生中随机抽取1名,抽到八年级女生的概率是0.19.
(1)求x的值.
(2)现用分层抽样的方法在全校抽取48名学生,问应在九年级抽取多少名?
(3)已知y≥245,z≥245,求九年级中女生比男生多的概率.
【答案与解析】
参考答案
1.【答案】B
【解析】E1与E3,E1与E4均为互斥而不对立的事件.
2.【答案】C
【解析】设某校毕业生的人数为x人,则每个学生上大学的概率为,所以x=100,则补习生的人数为12人,所以每个学生补习的概率为.
3.【答案】C
【解析】记事件A、B分别为“质量小于4.8 g”与“质量在[4.8,4.85)(g)”,又记事件C为“质量小于4.85 g”,则C=A+B,且A与B互斥,所以P(C)=P(A)+P(B),即0.32=0.3+P(A),解得P(A)=0.02.
4. 【答案】D
【解析】至少一次正面朝上的对立事件的概率为
5.【答案】C.
【解析】从标有1,2,3,4,5,6的6张纸片中任取2张,不同的取法种数是12、13、14、15、16、23、24、25、26、34、35、36、45、46、56共15种;
其中这2张纸片数字之积为6的取法种数是23、16;
∴对应的概率是.
故选:C.
6.【答案】A
【解析】记a,b分别为两个指针所落在区域中的数,则所有可能结果(a,b)有(1,1),(1,2),(1,3).(1,7),(1,8),(1,9),(2,1),…,(7,8),(7,9),即共有6×6=36(个),而(a,b)中的a,b均为奇数有(1,1),(1,3),(1,7),(1,9),(3,1),(3,3),(3,7),(3,9),(5,1),(5,3),(5,7),(5,9),(7,1),(7,3),(7,7),(7,9),共4×4=16(个),所以由古典概型的概率的计算公式得所求概率为.
7.【答案】C
【解析】考虑一趟渡船离开到下一趟渡船到达之间的1个小时为基本事件的全部,由几何概型可以求得,此人乘船过河的概率为.
8.【答案】B
【解析】因为三位数的正整数N共有900个,其中为一个正整数的N只有:27,28,29三个,所以所求的概率为.
9.【答案】6
【解析】某人打开电视看该台节目,看到广告的概率约为,所以该台每小时约有60×6(分钟)插播广告.
10.【答案】
【解析】从中任取两个球共有红1红2,红1白1,红1白2,红2白1,红2白1,红2白2,白1白2,共6种取法,其中颜相同只有2种,
故从中任取两个球,则这两个球颜色相同的概率;
故答案为:.
11.【答案】
【解析】由几何概型的计算公式知,,则.
12.【答案】
【解析】虽然摸球的顺序有先后,但只需不让后摸的人知道先摸者摸出的结果,那么各个摸球者摸到红球的概率都是相等的,并不因摸球的顺序不同而影响其公平性.
13.【解析】(1)由频率公式及题意可计算出优等品的频率依次为0.8,0.92,0.96,0.95,0.956,0.954.
(2)由(1)知,计算出的优等品的频率虽然各不相同,但都是在常数0.95附近摆动,因此,可估计该厂的电视机优等品的概率约是0.95.
14.【解析】设(x,y)表示一个基本事件,则掷两次骰子包括:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…,(6,5),(6,6),共36个基本事件.
(1)用A表示事件“x+y≤3”,
则A的结果有(1,1),(1,2),(2,1),共3个基本事件,
∵ P(A)=.
答:事件“x+y≤3”的概率为.
(2)用B表示事件“|x-y|=2”,
则B的结果有(1,3),(2,4),(3,5),(4,6),(6,4),(5,3),(4,2),(3,1),共8个基本事件,
∴ P(B)=.
答:事件“|x-y|=2”的概率为.
15.【答案】(1);(2)-2<b≤-1.
【解析】(1)b=―3时,直线为y=x―3,此时N(3,0),M(0,―3),
∴,
∵,
∴豆子落在三角形MNC内的概率为;
(2)四边形ABCD内的格点共有25个,落在三角形MNC(不含边界)内的格点有6个,
∴-2<b≤-1.
16.【解析】(1)∵ ,∴ x=380.
(2)九年级人数为y+z=2000-(373+377+380+370)=500,
现用分层抽样的方法在全校抽取48名学生,应在九年级抽取的人数为:名.
(3)设九年级女生比男生多的事件为A,九年级女生、男生数记为(y,z);
由(2)知y+z=500,且y,z∈N,基本事件有:
(245,255)、(246,254)、(247,253)、…、(255,245),共11个,
事件A包含的基本事件有:(251,249)、(252,248)、(253,247)、(254,246)、(255,245),共5个,∴ .
