高中数学必修三知识讲解,巩固练习(复习补习,期末复习资料):01【基础】算法与程序框图
文档属性
| 名称 | 高中数学必修三知识讲解,巩固练习(复习补习,期末复习资料):01【基础】算法与程序框图 |

|
|
| 格式 | zip | ||
| 文件大小 | 695.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 10:57:04 | ||
图片预览




文档简介
算法与程序框图
【学习目标】
1.初步建立算法的概念;
2.让学生通过丰富的实例体会算法的思想;
3.让学生通过对具体问题的探究,初步了解算法的含义;
4.掌握程序框图的概念;
5.会用通用的图形符号表示算法,掌握算法的三个基本逻辑结构;
6.掌握画程序框图的基本规则,能正确画出程序框图.
【要点梳理】
要点一、算法的概念
1、算法的定义:
广义的算法是指完成某项工作的方法和步骤,那么我们可以说洗衣机的使用说明书是操作洗衣机的算法,菜谱是做菜的算法等等.
在数学中,现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
2、算法的特征:
(1)确定性:算法的每一步都应当做到准确无误、“不重不漏”.“不重”是指不是可有可无的、甚至无用的步骤,“不漏”是指缺少哪一步都无法完成任务.
(2)逻辑性:算法从开始的“第一步”直到“最后一步”之间做到环环相扣,分工明确,“前一步”是“后一步”的前提,“后一步”是“前一步”的继续.
(3)有穷性:算法要有明确的开始和结束,当到达终止步骤时所要解决的问题必须有明确的结果,也就是说必须在有限步内完成任务,不能无限制的持续进行.
(4)不唯一性:求解某一个问题的算法不一定是唯一的,对于一个问题可以有不同的算法.
3、设计算法的要求
(1)写出的算法,必须能解决一类问题(如:判断一个整数35是否为质数;求任意一个方程的近似解……),并且能够重复使用.
(2)要使算法尽量简单、步骤尽量少.
(3)要保证算法正确.且计算机能够执行,如:让计算机计算1×2×3×4×5是可以做到的.
4、算法的描述:
(1)自然语言:自然语言就是人们日常使用的语言,可以是汉语、英语或数学语言等.用自然语言描述算法的优点是通俗易懂,当算法中的操作步骤都是顺序执行时比较容易理解.缺点是如果算法中包含判断和转向,并且操作步骤较多时,就不那么直观清晰了.
(2)程序框图:所谓框图,就是指用规定的图形符号来描述算法,用框图描述算法具有直观、结构清晰、条理分明、通俗易懂、便于检查修改及交流等特点.
(3)程序语言:算法最终可以通过程序的形式编写出来,并在计算机上执行.
要点诠释:
算法的特点:思路简单清晰,叙述复杂,步骤繁琐,计算量大,完全依靠人力难以完成,而这些恰恰就是计算机的特长,它能不厌其烦地完成枯燥的、重复的繁琐的工作,正因为这些,现代算法的作用之一就是使计算机代替人完成某些工作,这也是我们学习算法的重要原因之一.
事实上,算法中出现的程序只是用基本的语句把程序的主要结构描述出来,与真正的程序还有差距,所以算法描述的许多程序并不能直接运行,要运行程序,还要把程序按照某种语言的严格要求重新改写才行.
要点二、程序框图
1、程序框图的概念:
程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.
2、构成程序框的图形符号及其作用
程序框
名称
功能
起止框
表示一个算法的起始和结束,是任何算法程序框图不可缺少的.
输入、输出框
表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置.
处理框
赋值、计算.算法中处理数据需要的算式、公式等,它们分别写在不同的用以处理数据的处理框内.
判断框
判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时在出口处则标明“否”或“N”.
流程线
算法进行的前进方向以及先后顺序
连结点
连接另一页或另一部分的框图
3、程序框图的构成
一个程序框图包括以下几部分:实现不同算法功能的相对应的程序框;带箭头的流程线;程序框内必要的说明文字.
4、算法的三种基本逻辑结构
(1)顺序结构
顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的.它是由若干个依次执行的步骤组成的,它是任何一个算法都离不开的一种基本算法结构.
见示意图和实例:
/
顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤.如在示意图中,A框和B框是依次执行的,只有在执行完A框指定的操作后,才能接着执行B框所指定的操作.
(2)条件结构
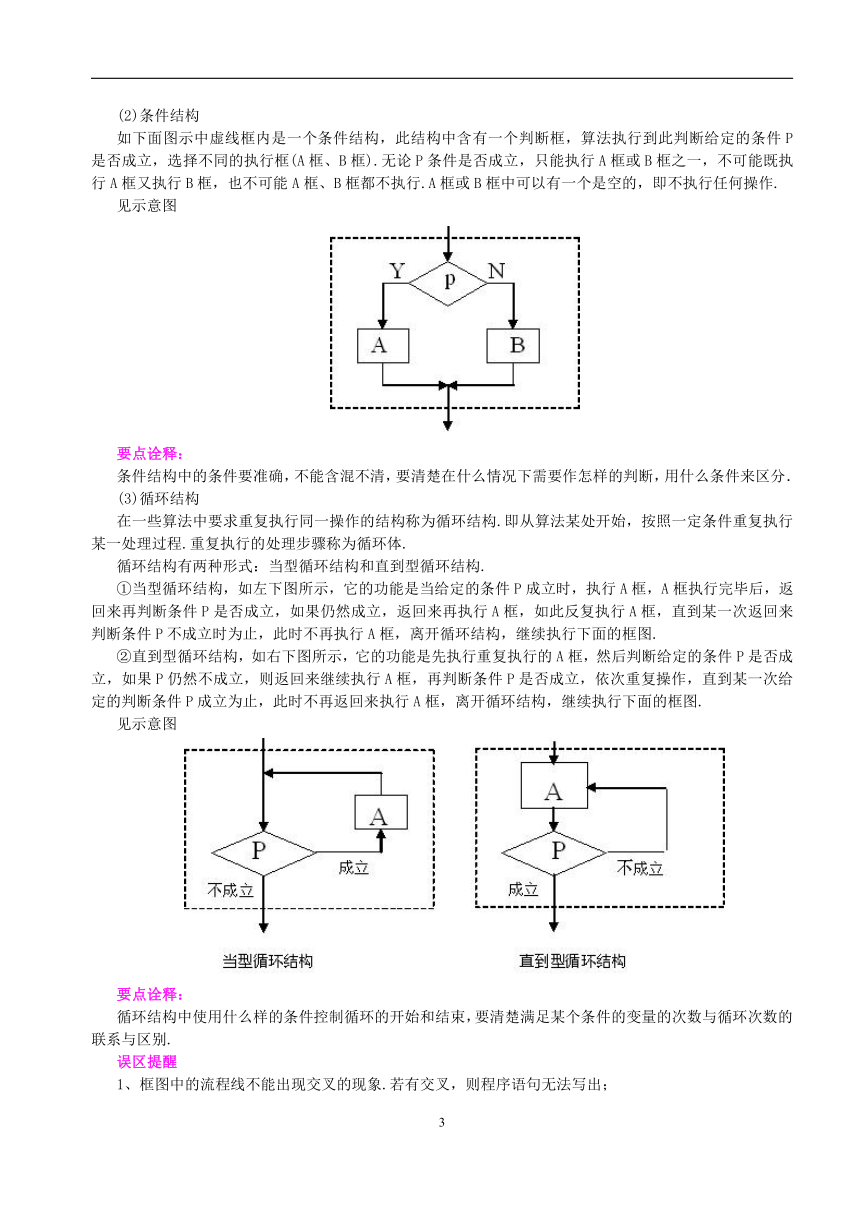
如下面图示中虚线框内是一个条件结构,此结构中含有一个判断框,算法执行到此判断给定的条件P是否成立,选择不同的执行框(A框、B框).无论P条件是否成立,只能执行A框或B框之一,不可能既执行A框又执行B框,也不可能A框、B框都不执行.A框或B框中可以有一个是空的,即不执行任何操作.
见示意图
/
要点诠释:
条件结构中的条件要准确,不能含混不清,要清楚在什么情况下需要作怎样的判断,用什么条件来区分.
(3)循环结构
在一些算法中要求重复执行同一操作的结构称为循环结构.即从算法某处开始,按照一定条件重复执行某一处理过程.重复执行的处理步骤称为循环体.
循环结构有两种形式:当型循环结构和直到型循环结构.
①当型循环结构,如左下图所示,它的功能是当给定的条件P成立时,执行A框,A框执行完毕后,返回来再判断条件P是否成立,如果仍然成立,返回来再执行A框,如此反复执行A框,直到某一次返回来判断条件P不成立时为止,此时不再执行A框,离开循环结构,继续执行下面的框图.
②直到型循环结构,如右下图所示,它的功能是先执行重复执行的A框,然后判断给定的条件P是否成立,如果P仍然不成立,则返回来继续执行A框,再判断条件P是否成立,依次重复操作,直到某一次给定的判断条件P成立为止,此时不再返回来执行A框,离开循环结构,继续执行下面的框图.
见示意图
/
要点诠释:
循环结构中使用什么样的条件控制循环的开始和结束,要清楚满足某个条件的变量的次数与循环次数的联系与区别.
误区提醒
1、框图中的流程线不能出现交叉的现象.若有交叉,则程序语句无法写出;
2、各种框图有其固定的格式和作用,不要乱用.如条件结构中不要忘了“是”与“否”,流程线不要忘记画箭头;
3、条件分支结构的方向要准确;
4、循环结构中,计数变量要赋初值,计数变量的自加不要忘记,自加多少不能弄错.另外计数变量一般只负责计数任务;
5、循环结构中循环的次数要严格把握,区分“<”与“≤”等.循环变量的取值与循环结构(当型与直到型)有关,需区分清楚.另外,同一问题用两种不同的结构解决时,其判断条件恰是相反的;
6、程序框图不要出现死循环(无限步的循环).
【典型例题】
类型一:算法的概念
例1.(1)下列描述不能看作算法的是( ).
A.做米饭需要刷锅,淘米,添水,加热这些步骤
B.洗衣机的使用说明书
C.解方程2x2+x-1=0
D.利用公式S=πr2,计算半径为4的圆的面积,就是计算π×42
(2)下列关于算法的说法:
①求解某一类问题的算法是唯一的;②算法必须在有限步操作之后停止;③算法的每一步操作必须是明确的,不能有歧义或模糊;④算法执行后一定产生明确的结果.
其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
【答案】(1)C (2)C
【解析】 (1)A、B、D都描述了解决问题的过程,可以看作算法.而C只描述了一个事实,没说明怎么解决问题,不是算法.
(2)根据算法的特征可以知道,算法要有明确的开始与结束,每一步操作都必须是明确而有效的,必须在有限步内得到明确的结果,所以②③④正确.而解决某一类问题的算法不一定是唯一的,故①错误.
【总结升华】算法一般是机械的,有时需要进行大量的重复计算,只要按部就班去做,总能算出结果.通常把算法过程称为“数学机械化”,数学机械化的最大优点是它可以借助计算机来完成.实际上处理任何问题都需要算法,如:中国象棋有中国象棋的棋谱、走法、胜负的评判准则;而国际象棋有国际象棋的棋谱、走法、胜负的评判准则;再比如申请出国有一系列的先后手续,购买物品也有相关的手续…….
举一反三:
【变式1】我们已学过的算法有求解一元二次方程的求根公式,加减消元法求二元一次方程组的解,二分法求出函数的零点等,对算法的描述有:①对一类问题都有效;②算法可执行的步骤必须是有限的;③算法可以一步一步地进行,每一步都有确切的含义;④是一种通法,只要按部就班地做,总能得到结果.以上算法的描述正确的有( ).
A.1个 B.2个 C.3个 D.4个
【答案】D
类型二:算法的描述
例2.写出求方程组的解的算法.
【解析】可利用消元法或代入法求解.
算法一:第一步:②×2+①,得到5x=14-4. ③
第二步,解方程③,可得x=2. ④
第三步,将④代入②,可得2+y=-2. ⑤
第四步,解⑤得y=-4.
第五步,得到方程组的解为
算法二:第一步,由②式移项可以得到x=-2-y. ③
第二步,把③代入①,得y=-4. ④
第三步,把④代入③,得x=2.
第四步,得到方程组的解为.
【总结升华】 通过求解二元一次方程组可知,求解某个问题的算法不一定唯一.对于具体的实例可以选择合适的算法,尽量做到“省时省力”,使所用的算法是最优算法.
举一反三:
【变式1】试描述求解三元一次方程组的算法步骤.
【解析】
算法1:第一步,①+③,得x=5. ④
第二步,将④分别代入①式和②式可得.
第三步,⑥-⑤,得y=-4. ⑦
第四步,将⑦代入⑤可得 z=11.
第五步,得到方程组的解为.
算法2:第一步,①+②,得2x-y=14. ④
第二步,②-③,得x-y=9. ⑤
第三步,④-⑤,得x=5. ⑥
第四步,将⑥代入⑤式,得y=-4. ⑦
第五步,将⑥和⑦代入①式,得z=11.
第六步,得到方程组的解为.
类型三:算法的设计
例3.设计一个算法,从3个互不相等的数中选出最小的一个数.,并用数学语言表达.
【解析】第一步:假定这3个数中第一个是“最小值”;
第二步:将第二个数与“最小值”比较,如果它小于此“最小值”,那么就用这个数取代“最小值”;
第三步:再重复第二步,将第三个数与最小值比较,如果它小于此“最小值”,那么就用这个数取代“最小值”;
第四步:此时的“最小值”就是三个数中的最小值,输出最小值.
所谓的算法,就是解决该类问题的一般步骤.
举一反三:
【变式1】任意给定一个正整数n,设计出判断n是否为质数的一个算法.
【解析】第一步,当n=1时,n既不是质数,也不是合数;
第二步,当n=2时,n是质数;
第三步,当n≥3时,从2到n-1依次判断是否存在n的因数(因数1除外),若存在,则n是合数;若不存在,则n是质数.
类型四:顺序结构的应用
例4.对于一个二次函数,求出顶点坐标.
【解析】算法步骤:
S1 用户输入二次函数的系数a,b,c;
S2 计算顶点坐标(赋值);
S3 输出顶点坐标.
算法框图:
举一反三:
【变式1】已知x=40,y=3.画出计算z=15x+8y的值的程序框图.
【答案】程序框图如下图所示.
/
类型五:条件结构的应用
例5.已知函数,写出求该函数的函数值的算法,并画出程序框图.
【解析】该函数是分段函数,因此当给出一个自变量x的值时,需先判断x的范围,然后确定利用哪一段的解析式求函数值.画程序框图时,必须采用条件分支结构,因为函数解析式分了三段,所以需要两个判断框,即进行两次判断.
算法如下:
第一步,输入x.
第二步,如果x<0,那么使y=2x-1,输出y;否则,执行第三步.
第三步,如果0≤x<1,那么使y=x2+1,输出y;否则,执行第四步.
第四步,y=x2+2x
第五步,输出y.
程序框图如下图所示.
/
【总结升华】凡是必须先根据条件作出判断,然后再决定进行哪一个步骤的问题,在画程序框图时,必须引入判断框,采用条件结构.而像本题求分段函数的函数值的程序框图的画法,如果是分两段的函数,只需引入一个判断框;如果是分三段的函数,需引入两个判断框;分四段的函数需引入三个判断框,依此类推.判断框内的内容是没有固定顺序的.
举一反三:
【变式1】已知函数, 写出求函数的任一函数值的一个算法并画出程序框图.
【解析】记y=f (x).
算法:
第一步:输入x.
第二步:如果x>0,那么使y=-1;如果x=0,那么使y=0;如果x<0,那么使y=1.
第三步:输出函数值y.
程序框图如下图所示.
/
【变式2】如果学生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”.用程序框图表示这一算法过程.
【答案】
类型六:循环结构的应用
例6.设计一个计算1+3+5+7+…+999的值的算法,并画出程序框图.
【解析】算法一:当型循环:第一步,令S=0,i=1.
第二步,若i≤999成立,则执行第三步;否则输出S,结束算法.
第三步,S=S+i.
第四步,i=i+2,返回第二步,程序框图如图(1).
/
算法二:直到型循环:第一步,令S=0,i=1.
第二步,S=S+i.
第三步,i=i+2.
第四步,若i不大于999,转第二步;否则,输出S,结束算法.程序框图如图1-1-8(2).
【总结升华】注意直到型循环和当型循环的区别.直到型循环先执行i=i+2,再判断i>999是否成立,若成立才输出S;而当型循环先判断i≤999是否成立,若成立,则执行i=i+2,直到条件i≤999不成立才结束循环,输出S.
举一反三:
【变式1】给出30个数:1,2,4,7,11,…,要计算这30个数的和,现已给出了该问题的程序框图如图所示,那么框图中判断框处①和执行框②处应分别填入( )
A.i≤30?;p=p+i-1 B.i≤31?;p=p+i+1
C.i≤31?;p=p+i D.i≤30?;p=p+i
【答案】D
【解析】由于要计算30个数的和,
故循环要执行30次,由于循环变量的初值为1,步长为1,故终值应为30
即①中应填写i≤30;
又由第1个数是1;
第2个数比第1个数大1,即1+1=2;
第3个数比第2个数大1,即2+2=4;
第4个数比第3个数大1,即4+3=7;…
故②中应填写p=p+i
故选:D.
【变式2】(2017春 河南周口期中)设计求1+3+5+7+…+31的算法,并画出相应的程序框图.
【解析】第一步:S=0;
第二步:i=1;
第三步:S=S+i;
第四步:i=i+2;
第五步:若i不大于31,返回执行第三步,否则执行第六步;
第六步:输出S值.
程序框图如图:
/
类型七:利用算法和程序框图解决实际问题
例7.北京获得了2008年第29届奥运会主办权.你知道在申办奥运会的最后阶段,国际奥委会是如何通过投票决定主办权归属的吗?
对选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票超过总票数的一半,那么该城市就获得主办权;如果所有申办城市得票数都不超过总票数的一半,则将得票最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止.试画出该过程的程序框图.
【解析】本题为算法中与现实生活相联系的题目,从选举的方法看,应选择循环结构来描述算法.
如图所示:
/
【总结升华】 解决与现实相关的问题时首先要理清题意,此循环结构中对用哪一个步骤控制循环,哪一个步骤作为循环体,要有清晰的思路.
举一反三:
【变式1】儿童乘坐火车时,若身高不超过1.1 m,则无需购票;若身高超过1.1 m,但不超过1.4 m,可买半票;若超过1.4 m,应买全票,请设计一个算法,并画出程序框图.
【解析】根据题意,该题的算法中应用条件结构,首先以身高为标准,分成买和免票,在买票中再分出半票和全票.
买票的算法步骤如下:
第一步:测量儿童身高h.
第二步:如果h≤1.1 m,那么免费乘车,否则若h≤1.4 m,则买半票,否则买全票.
程序框图如下图所示.
/
【总结升华】本题的程序框图中有两个判断点,一个是以1.1 m为判断点,1.1 m把身高分为两段,在大于1.1 m的一段中,1.4 m又将其分两段,因此1.4 m这个判断是套在1.1 m的判断里的.所以我们用到两个条件结构.
【巩固练习】
1.下列说法正确的是( ).
A.一个算法的步骤是可逆的
B.一个算法可以无止境地运算下去
C.完成一件事情的算法有且只有一种
D.设计算法要本着简单方便的原则
2.早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个过程.从下列选项中选出最好的一种算法( ).
A.第一步,洗脸刷牙.第二步,刷水壶.第三步,烧水.第四步,泡面.第五步,吃饭.第六步,听广播
B.第一步,刷水壶.第二步,烧水同时洗脸刷牙.第三步,泡面.第四步,吃饭.第五步,听广播
C.第一步,刷水壶.第二步,烧水同时洗脸刷牙.第三步,泡面.第四步,吃饭同时听广播
D.第一步,吃饭同时听广播.第二步,泡面.第三步,烧水同时洗脸刷牙.第四步,刷水壶
3.下面四种叙述能称为算法的是( )
A.在家里一般是妈妈做饭
B.做米饭需要刷锅、淘米、添水、加热这些步骤
C.在野外做饭叫野炊
D.做饭必须要有米
4.程序框图中“处理框”的功能是( )
A.赋值 B.计算 C.赋值或计算 D.判断某一条件是否成立
5.如下图(左)所示的是一个算法的程序框图,已知a1=3,输出的结果为7,则a2的值是( )
A.9 B.10 C.11 D.12
/
6.输入―1,按上图(右)所示的程序框图运行后,输出的结果是( )
A.―1 B.0 C.1 D.2
7.(2017 淮南模拟)下面的程序框图能判断任意输入的数x的奇偶性.其中判断框内的条件是( )
/
A.m=0 B.m=1 C.x=0 D.x=1
8.某程序框图如下图所示,该程序运行后输出的倒数第二个数是( )
A. B. C. D.
/
9.完成不等式的算法过程:
(1)将含的项移项至不等式的左边,将常数项移至不等式的右边,得 ;
(2)在不等式两边同时除以的系数,得 .
10.写出下列算法的功能.
(1)图(左)中算法的功能是(a>0,b>0)________;
(2)图(右)中算法的功能是______________________.
/
11.如图所示是求小于等于1000的所有正偶数的和的程序框图,则空白处①应为 ;②应为
.
/
12.(2018 马鞍山三模)如图是一算法的程序框图,若此程序运行结果为S=720,则在判断框中应填入关于k的判断条件是 .
13.(2017春 河南南阳月考)以下是某次考试中某班10名同学的数学成绩(单位:分)82,120,97,65,130,115,98,107,77,89.要求将90分以上的同学的平均分求出来.画出算法框图,并写出程序语句.
14.(2018春 娄底期中)已知一个三角形的三边边长为2,3,4,设计一个算法,求出它的面积.
15.火车站对乘客退票收取一定的费用,具体办法是:按票价每10元(不足10元按10元计算)核收2元;2元以下的票不退.试写出票价为x元的车票退掉后,返还的金额y元的算法的程序框图.
【答案与解析】
1.【答案】D
【解析】由算法的定义与特征可得.
2.【答案】C
【解析】因为A选项共用时间36 min,B选项共用时间31 min,C选项共用时间23 min,D选项的算法步骤不符合常理.
3.【答案】B
【解析】算法的特点:有穷性,确定性,顺序性与正确性,不唯一性,普通性
算法可以用自然语言、图形语言、程序语言来表示,同一问题可以用不同的算法来描述,但结果一定相同,
故选:B
4.【答案】C
5.【答案】C
【解析】 根据算法的程序框图可知此处求的是,因为输出的结果是7,所以a1+a2=14,又a1=3,从而a2=11.
6.【答案】B
【解析】根据程序框图应当执行“y=x2-1”这个处理框,从而有y=0,故选B.
7.【答案】B
【解析】由程序框图所体现的算法可知判断一个数是奇数还是偶数,看这个数除以2的余数是1还是0.
由图可知应该填m=1.
故选B.
8.【答案】C
【解析】由程序框图知,输出的数依次为3,2,,,.所以该程序运行后输出的倒数第二个数是.
9.【答案】(1);(2)
10.【答案】(1)求以a,b为直角边的直角三角形斜边c的长
(2)求两个实数a,b的和
【解析】这两个框图均为顺序结构,直接可看出答案.
11.【答案】
12.【答案】k≥8或k>7
【解析】S=720=1×10×9×8
所以循环体执行三次
则判断框中应填入关于k的判断条件是k≥8或k>7
故答案:k≥8或k>7
13.【解析】算法框图如下:
/
算法语句如下:
i=1
s=0
m=0
DO
INPUT x
IF x>=90 THEN
s=s+x
m=m+1
END IF
i=i+1
LOOP WHILE i<=10
P=s/m
PRINT P
END
14.【解析】由于已知三角形的三边长,可利用海伦公式求三角形的面积,具体算法如下:
第一步,令a=2,b=3,c=4
第二步,计算
第三步,利用公式,求出面积
第四步,输出S,结束程序
15.【解析】
【学习目标】
1.初步建立算法的概念;
2.让学生通过丰富的实例体会算法的思想;
3.让学生通过对具体问题的探究,初步了解算法的含义;
4.掌握程序框图的概念;
5.会用通用的图形符号表示算法,掌握算法的三个基本逻辑结构;
6.掌握画程序框图的基本规则,能正确画出程序框图.
【要点梳理】
要点一、算法的概念
1、算法的定义:
广义的算法是指完成某项工作的方法和步骤,那么我们可以说洗衣机的使用说明书是操作洗衣机的算法,菜谱是做菜的算法等等.
在数学中,现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
2、算法的特征:
(1)确定性:算法的每一步都应当做到准确无误、“不重不漏”.“不重”是指不是可有可无的、甚至无用的步骤,“不漏”是指缺少哪一步都无法完成任务.
(2)逻辑性:算法从开始的“第一步”直到“最后一步”之间做到环环相扣,分工明确,“前一步”是“后一步”的前提,“后一步”是“前一步”的继续.
(3)有穷性:算法要有明确的开始和结束,当到达终止步骤时所要解决的问题必须有明确的结果,也就是说必须在有限步内完成任务,不能无限制的持续进行.
(4)不唯一性:求解某一个问题的算法不一定是唯一的,对于一个问题可以有不同的算法.
3、设计算法的要求
(1)写出的算法,必须能解决一类问题(如:判断一个整数35是否为质数;求任意一个方程的近似解……),并且能够重复使用.
(2)要使算法尽量简单、步骤尽量少.
(3)要保证算法正确.且计算机能够执行,如:让计算机计算1×2×3×4×5是可以做到的.
4、算法的描述:
(1)自然语言:自然语言就是人们日常使用的语言,可以是汉语、英语或数学语言等.用自然语言描述算法的优点是通俗易懂,当算法中的操作步骤都是顺序执行时比较容易理解.缺点是如果算法中包含判断和转向,并且操作步骤较多时,就不那么直观清晰了.
(2)程序框图:所谓框图,就是指用规定的图形符号来描述算法,用框图描述算法具有直观、结构清晰、条理分明、通俗易懂、便于检查修改及交流等特点.
(3)程序语言:算法最终可以通过程序的形式编写出来,并在计算机上执行.
要点诠释:
算法的特点:思路简单清晰,叙述复杂,步骤繁琐,计算量大,完全依靠人力难以完成,而这些恰恰就是计算机的特长,它能不厌其烦地完成枯燥的、重复的繁琐的工作,正因为这些,现代算法的作用之一就是使计算机代替人完成某些工作,这也是我们学习算法的重要原因之一.
事实上,算法中出现的程序只是用基本的语句把程序的主要结构描述出来,与真正的程序还有差距,所以算法描述的许多程序并不能直接运行,要运行程序,还要把程序按照某种语言的严格要求重新改写才行.
要点二、程序框图
1、程序框图的概念:
程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.
2、构成程序框的图形符号及其作用
程序框
名称
功能
起止框
表示一个算法的起始和结束,是任何算法程序框图不可缺少的.
输入、输出框
表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置.
处理框
赋值、计算.算法中处理数据需要的算式、公式等,它们分别写在不同的用以处理数据的处理框内.
判断框
判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时在出口处则标明“否”或“N”.
流程线
算法进行的前进方向以及先后顺序
连结点
连接另一页或另一部分的框图
3、程序框图的构成
一个程序框图包括以下几部分:实现不同算法功能的相对应的程序框;带箭头的流程线;程序框内必要的说明文字.
4、算法的三种基本逻辑结构
(1)顺序结构
顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的.它是由若干个依次执行的步骤组成的,它是任何一个算法都离不开的一种基本算法结构.
见示意图和实例:
/
顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤.如在示意图中,A框和B框是依次执行的,只有在执行完A框指定的操作后,才能接着执行B框所指定的操作.
(2)条件结构
如下面图示中虚线框内是一个条件结构,此结构中含有一个判断框,算法执行到此判断给定的条件P是否成立,选择不同的执行框(A框、B框).无论P条件是否成立,只能执行A框或B框之一,不可能既执行A框又执行B框,也不可能A框、B框都不执行.A框或B框中可以有一个是空的,即不执行任何操作.
见示意图
/
要点诠释:
条件结构中的条件要准确,不能含混不清,要清楚在什么情况下需要作怎样的判断,用什么条件来区分.
(3)循环结构
在一些算法中要求重复执行同一操作的结构称为循环结构.即从算法某处开始,按照一定条件重复执行某一处理过程.重复执行的处理步骤称为循环体.
循环结构有两种形式:当型循环结构和直到型循环结构.
①当型循环结构,如左下图所示,它的功能是当给定的条件P成立时,执行A框,A框执行完毕后,返回来再判断条件P是否成立,如果仍然成立,返回来再执行A框,如此反复执行A框,直到某一次返回来判断条件P不成立时为止,此时不再执行A框,离开循环结构,继续执行下面的框图.
②直到型循环结构,如右下图所示,它的功能是先执行重复执行的A框,然后判断给定的条件P是否成立,如果P仍然不成立,则返回来继续执行A框,再判断条件P是否成立,依次重复操作,直到某一次给定的判断条件P成立为止,此时不再返回来执行A框,离开循环结构,继续执行下面的框图.
见示意图
/
要点诠释:
循环结构中使用什么样的条件控制循环的开始和结束,要清楚满足某个条件的变量的次数与循环次数的联系与区别.
误区提醒
1、框图中的流程线不能出现交叉的现象.若有交叉,则程序语句无法写出;
2、各种框图有其固定的格式和作用,不要乱用.如条件结构中不要忘了“是”与“否”,流程线不要忘记画箭头;
3、条件分支结构的方向要准确;
4、循环结构中,计数变量要赋初值,计数变量的自加不要忘记,自加多少不能弄错.另外计数变量一般只负责计数任务;
5、循环结构中循环的次数要严格把握,区分“<”与“≤”等.循环变量的取值与循环结构(当型与直到型)有关,需区分清楚.另外,同一问题用两种不同的结构解决时,其判断条件恰是相反的;
6、程序框图不要出现死循环(无限步的循环).
【典型例题】
类型一:算法的概念
例1.(1)下列描述不能看作算法的是( ).
A.做米饭需要刷锅,淘米,添水,加热这些步骤
B.洗衣机的使用说明书
C.解方程2x2+x-1=0
D.利用公式S=πr2,计算半径为4的圆的面积,就是计算π×42
(2)下列关于算法的说法:
①求解某一类问题的算法是唯一的;②算法必须在有限步操作之后停止;③算法的每一步操作必须是明确的,不能有歧义或模糊;④算法执行后一定产生明确的结果.
其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
【答案】(1)C (2)C
【解析】 (1)A、B、D都描述了解决问题的过程,可以看作算法.而C只描述了一个事实,没说明怎么解决问题,不是算法.
(2)根据算法的特征可以知道,算法要有明确的开始与结束,每一步操作都必须是明确而有效的,必须在有限步内得到明确的结果,所以②③④正确.而解决某一类问题的算法不一定是唯一的,故①错误.
【总结升华】算法一般是机械的,有时需要进行大量的重复计算,只要按部就班去做,总能算出结果.通常把算法过程称为“数学机械化”,数学机械化的最大优点是它可以借助计算机来完成.实际上处理任何问题都需要算法,如:中国象棋有中国象棋的棋谱、走法、胜负的评判准则;而国际象棋有国际象棋的棋谱、走法、胜负的评判准则;再比如申请出国有一系列的先后手续,购买物品也有相关的手续…….
举一反三:
【变式1】我们已学过的算法有求解一元二次方程的求根公式,加减消元法求二元一次方程组的解,二分法求出函数的零点等,对算法的描述有:①对一类问题都有效;②算法可执行的步骤必须是有限的;③算法可以一步一步地进行,每一步都有确切的含义;④是一种通法,只要按部就班地做,总能得到结果.以上算法的描述正确的有( ).
A.1个 B.2个 C.3个 D.4个
【答案】D
类型二:算法的描述
例2.写出求方程组的解的算法.
【解析】可利用消元法或代入法求解.
算法一:第一步:②×2+①,得到5x=14-4. ③
第二步,解方程③,可得x=2. ④
第三步,将④代入②,可得2+y=-2. ⑤
第四步,解⑤得y=-4.
第五步,得到方程组的解为
算法二:第一步,由②式移项可以得到x=-2-y. ③
第二步,把③代入①,得y=-4. ④
第三步,把④代入③,得x=2.
第四步,得到方程组的解为.
【总结升华】 通过求解二元一次方程组可知,求解某个问题的算法不一定唯一.对于具体的实例可以选择合适的算法,尽量做到“省时省力”,使所用的算法是最优算法.
举一反三:
【变式1】试描述求解三元一次方程组的算法步骤.
【解析】
算法1:第一步,①+③,得x=5. ④
第二步,将④分别代入①式和②式可得.
第三步,⑥-⑤,得y=-4. ⑦
第四步,将⑦代入⑤可得 z=11.
第五步,得到方程组的解为.
算法2:第一步,①+②,得2x-y=14. ④
第二步,②-③,得x-y=9. ⑤
第三步,④-⑤,得x=5. ⑥
第四步,将⑥代入⑤式,得y=-4. ⑦
第五步,将⑥和⑦代入①式,得z=11.
第六步,得到方程组的解为.
类型三:算法的设计
例3.设计一个算法,从3个互不相等的数中选出最小的一个数.,并用数学语言表达.
【解析】第一步:假定这3个数中第一个是“最小值”;
第二步:将第二个数与“最小值”比较,如果它小于此“最小值”,那么就用这个数取代“最小值”;
第三步:再重复第二步,将第三个数与最小值比较,如果它小于此“最小值”,那么就用这个数取代“最小值”;
第四步:此时的“最小值”就是三个数中的最小值,输出最小值.
所谓的算法,就是解决该类问题的一般步骤.
举一反三:
【变式1】任意给定一个正整数n,设计出判断n是否为质数的一个算法.
【解析】第一步,当n=1时,n既不是质数,也不是合数;
第二步,当n=2时,n是质数;
第三步,当n≥3时,从2到n-1依次判断是否存在n的因数(因数1除外),若存在,则n是合数;若不存在,则n是质数.
类型四:顺序结构的应用
例4.对于一个二次函数,求出顶点坐标.
【解析】算法步骤:
S1 用户输入二次函数的系数a,b,c;
S2 计算顶点坐标(赋值);
S3 输出顶点坐标.
算法框图:
举一反三:
【变式1】已知x=40,y=3.画出计算z=15x+8y的值的程序框图.
【答案】程序框图如下图所示.
/
类型五:条件结构的应用
例5.已知函数,写出求该函数的函数值的算法,并画出程序框图.
【解析】该函数是分段函数,因此当给出一个自变量x的值时,需先判断x的范围,然后确定利用哪一段的解析式求函数值.画程序框图时,必须采用条件分支结构,因为函数解析式分了三段,所以需要两个判断框,即进行两次判断.
算法如下:
第一步,输入x.
第二步,如果x<0,那么使y=2x-1,输出y;否则,执行第三步.
第三步,如果0≤x<1,那么使y=x2+1,输出y;否则,执行第四步.
第四步,y=x2+2x
第五步,输出y.
程序框图如下图所示.
/
【总结升华】凡是必须先根据条件作出判断,然后再决定进行哪一个步骤的问题,在画程序框图时,必须引入判断框,采用条件结构.而像本题求分段函数的函数值的程序框图的画法,如果是分两段的函数,只需引入一个判断框;如果是分三段的函数,需引入两个判断框;分四段的函数需引入三个判断框,依此类推.判断框内的内容是没有固定顺序的.
举一反三:
【变式1】已知函数, 写出求函数的任一函数值的一个算法并画出程序框图.
【解析】记y=f (x).
算法:
第一步:输入x.
第二步:如果x>0,那么使y=-1;如果x=0,那么使y=0;如果x<0,那么使y=1.
第三步:输出函数值y.
程序框图如下图所示.
/
【变式2】如果学生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”.用程序框图表示这一算法过程.
【答案】
类型六:循环结构的应用
例6.设计一个计算1+3+5+7+…+999的值的算法,并画出程序框图.
【解析】算法一:当型循环:第一步,令S=0,i=1.
第二步,若i≤999成立,则执行第三步;否则输出S,结束算法.
第三步,S=S+i.
第四步,i=i+2,返回第二步,程序框图如图(1).
/
算法二:直到型循环:第一步,令S=0,i=1.
第二步,S=S+i.
第三步,i=i+2.
第四步,若i不大于999,转第二步;否则,输出S,结束算法.程序框图如图1-1-8(2).
【总结升华】注意直到型循环和当型循环的区别.直到型循环先执行i=i+2,再判断i>999是否成立,若成立才输出S;而当型循环先判断i≤999是否成立,若成立,则执行i=i+2,直到条件i≤999不成立才结束循环,输出S.
举一反三:
【变式1】给出30个数:1,2,4,7,11,…,要计算这30个数的和,现已给出了该问题的程序框图如图所示,那么框图中判断框处①和执行框②处应分别填入( )
A.i≤30?;p=p+i-1 B.i≤31?;p=p+i+1
C.i≤31?;p=p+i D.i≤30?;p=p+i
【答案】D
【解析】由于要计算30个数的和,
故循环要执行30次,由于循环变量的初值为1,步长为1,故终值应为30
即①中应填写i≤30;
又由第1个数是1;
第2个数比第1个数大1,即1+1=2;
第3个数比第2个数大1,即2+2=4;
第4个数比第3个数大1,即4+3=7;…
故②中应填写p=p+i
故选:D.
【变式2】(2017春 河南周口期中)设计求1+3+5+7+…+31的算法,并画出相应的程序框图.
【解析】第一步:S=0;
第二步:i=1;
第三步:S=S+i;
第四步:i=i+2;
第五步:若i不大于31,返回执行第三步,否则执行第六步;
第六步:输出S值.
程序框图如图:
/
类型七:利用算法和程序框图解决实际问题
例7.北京获得了2008年第29届奥运会主办权.你知道在申办奥运会的最后阶段,国际奥委会是如何通过投票决定主办权归属的吗?
对选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票超过总票数的一半,那么该城市就获得主办权;如果所有申办城市得票数都不超过总票数的一半,则将得票最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止.试画出该过程的程序框图.
【解析】本题为算法中与现实生活相联系的题目,从选举的方法看,应选择循环结构来描述算法.
如图所示:
/
【总结升华】 解决与现实相关的问题时首先要理清题意,此循环结构中对用哪一个步骤控制循环,哪一个步骤作为循环体,要有清晰的思路.
举一反三:
【变式1】儿童乘坐火车时,若身高不超过1.1 m,则无需购票;若身高超过1.1 m,但不超过1.4 m,可买半票;若超过1.4 m,应买全票,请设计一个算法,并画出程序框图.
【解析】根据题意,该题的算法中应用条件结构,首先以身高为标准,分成买和免票,在买票中再分出半票和全票.
买票的算法步骤如下:
第一步:测量儿童身高h.
第二步:如果h≤1.1 m,那么免费乘车,否则若h≤1.4 m,则买半票,否则买全票.
程序框图如下图所示.
/
【总结升华】本题的程序框图中有两个判断点,一个是以1.1 m为判断点,1.1 m把身高分为两段,在大于1.1 m的一段中,1.4 m又将其分两段,因此1.4 m这个判断是套在1.1 m的判断里的.所以我们用到两个条件结构.
【巩固练习】
1.下列说法正确的是( ).
A.一个算法的步骤是可逆的
B.一个算法可以无止境地运算下去
C.完成一件事情的算法有且只有一种
D.设计算法要本着简单方便的原则
2.早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个过程.从下列选项中选出最好的一种算法( ).
A.第一步,洗脸刷牙.第二步,刷水壶.第三步,烧水.第四步,泡面.第五步,吃饭.第六步,听广播
B.第一步,刷水壶.第二步,烧水同时洗脸刷牙.第三步,泡面.第四步,吃饭.第五步,听广播
C.第一步,刷水壶.第二步,烧水同时洗脸刷牙.第三步,泡面.第四步,吃饭同时听广播
D.第一步,吃饭同时听广播.第二步,泡面.第三步,烧水同时洗脸刷牙.第四步,刷水壶
3.下面四种叙述能称为算法的是( )
A.在家里一般是妈妈做饭
B.做米饭需要刷锅、淘米、添水、加热这些步骤
C.在野外做饭叫野炊
D.做饭必须要有米
4.程序框图中“处理框”的功能是( )
A.赋值 B.计算 C.赋值或计算 D.判断某一条件是否成立
5.如下图(左)所示的是一个算法的程序框图,已知a1=3,输出的结果为7,则a2的值是( )
A.9 B.10 C.11 D.12
/
6.输入―1,按上图(右)所示的程序框图运行后,输出的结果是( )
A.―1 B.0 C.1 D.2
7.(2017 淮南模拟)下面的程序框图能判断任意输入的数x的奇偶性.其中判断框内的条件是( )
/
A.m=0 B.m=1 C.x=0 D.x=1
8.某程序框图如下图所示,该程序运行后输出的倒数第二个数是( )
A. B. C. D.
/
9.完成不等式的算法过程:
(1)将含的项移项至不等式的左边,将常数项移至不等式的右边,得 ;
(2)在不等式两边同时除以的系数,得 .
10.写出下列算法的功能.
(1)图(左)中算法的功能是(a>0,b>0)________;
(2)图(右)中算法的功能是______________________.
/
11.如图所示是求小于等于1000的所有正偶数的和的程序框图,则空白处①应为 ;②应为
.
/
12.(2018 马鞍山三模)如图是一算法的程序框图,若此程序运行结果为S=720,则在判断框中应填入关于k的判断条件是 .
13.(2017春 河南南阳月考)以下是某次考试中某班10名同学的数学成绩(单位:分)82,120,97,65,130,115,98,107,77,89.要求将90分以上的同学的平均分求出来.画出算法框图,并写出程序语句.
14.(2018春 娄底期中)已知一个三角形的三边边长为2,3,4,设计一个算法,求出它的面积.
15.火车站对乘客退票收取一定的费用,具体办法是:按票价每10元(不足10元按10元计算)核收2元;2元以下的票不退.试写出票价为x元的车票退掉后,返还的金额y元的算法的程序框图.
【答案与解析】
1.【答案】D
【解析】由算法的定义与特征可得.
2.【答案】C
【解析】因为A选项共用时间36 min,B选项共用时间31 min,C选项共用时间23 min,D选项的算法步骤不符合常理.
3.【答案】B
【解析】算法的特点:有穷性,确定性,顺序性与正确性,不唯一性,普通性
算法可以用自然语言、图形语言、程序语言来表示,同一问题可以用不同的算法来描述,但结果一定相同,
故选:B
4.【答案】C
5.【答案】C
【解析】 根据算法的程序框图可知此处求的是,因为输出的结果是7,所以a1+a2=14,又a1=3,从而a2=11.
6.【答案】B
【解析】根据程序框图应当执行“y=x2-1”这个处理框,从而有y=0,故选B.
7.【答案】B
【解析】由程序框图所体现的算法可知判断一个数是奇数还是偶数,看这个数除以2的余数是1还是0.
由图可知应该填m=1.
故选B.
8.【答案】C
【解析】由程序框图知,输出的数依次为3,2,,,.所以该程序运行后输出的倒数第二个数是.
9.【答案】(1);(2)
10.【答案】(1)求以a,b为直角边的直角三角形斜边c的长
(2)求两个实数a,b的和
【解析】这两个框图均为顺序结构,直接可看出答案.
11.【答案】
12.【答案】k≥8或k>7
【解析】S=720=1×10×9×8
所以循环体执行三次
则判断框中应填入关于k的判断条件是k≥8或k>7
故答案:k≥8或k>7
13.【解析】算法框图如下:
/
算法语句如下:
i=1
s=0
m=0
DO
INPUT x
IF x>=90 THEN
s=s+x
m=m+1
END IF
i=i+1
LOOP WHILE i<=10
P=s/m
PRINT P
END
14.【解析】由于已知三角形的三边长,可利用海伦公式求三角形的面积,具体算法如下:
第一步,令a=2,b=3,c=4
第二步,计算
第三步,利用公式,求出面积
第四步,输出S,结束程序
15.【解析】
