高中数学必修三知识讲解,巩固练习(复习补习,期末复习资料):06【提高】算法案例
文档属性
| 名称 | 高中数学必修三知识讲解,巩固练习(复习补习,期末复习资料):06【提高】算法案例 |
|
|
| 格式 | zip | ||
| 文件大小 | 230.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-18 00:00:00 | ||
图片预览





文档简介
算法案例
【学习目标】
1.理解辗转相除法与更相减损术中蕴含的数学原理,并能根据这些原理进行算法分析;
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序;
3.了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质;
4.了解各种进位制与十进制之间转换的规律,会利用各种进位制与十进制之间的联系进行各种进位制之间的转换.
【要点梳理】
要点一:辗转相除法
也叫欧几里德算法,它是由欧几里德在公元前300年左右首先提出的.利用辗转相除法求最大公约数的步骤如下:
第一步:用较大的数m除以较小的数n得到一个商q0和一个余数r0;
第二步:若r0=0,则n为m,n的最大公约数;若r0≠0,则用除数n除以余数r0得到一个商q1和一个余数r1;
第三步:若r1=0,则r0为m,n的最大公约数;若r1≠0,则用除数r0除以余数r1得到一个商q2和一个余数r2;
……
依次计算直至rn=0,此时所得到的rn-1即为所求的最大公约数.
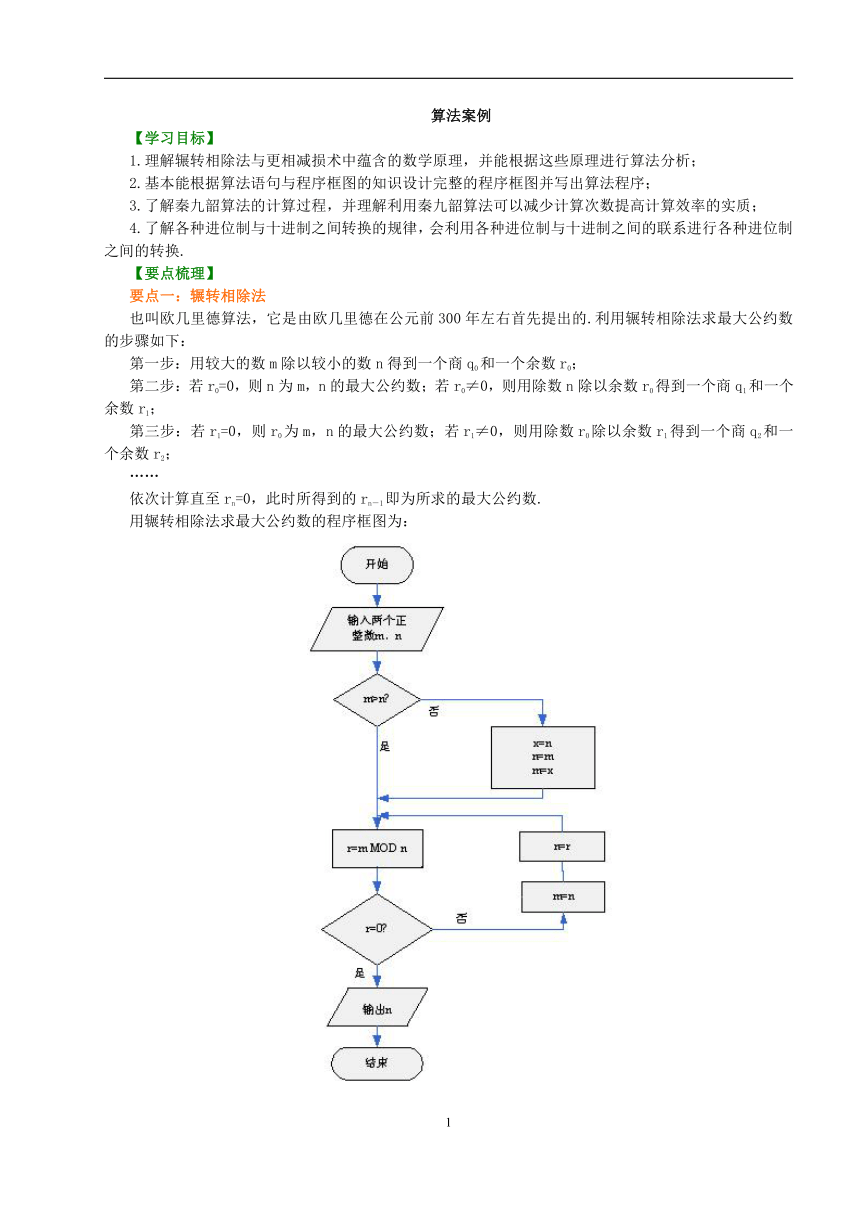
用辗转相除法求最大公约数的程序框图为:
/
程序:
INPUT “m=”;m
INPUT “n=”;n
IF mx=m
m=n
n=x
END IF
r=m MOD n
WHILE r<>0
r=m MOD n
m=n
n=r
WEND
PRINT n
END
要点诠释:
辗转相除法的基本步骤是用较大的数除以较小的数,考虑到算法中的赋值语句可以对同一变量多次赋值,我们可以把较大的数用变量m表示,把较小的数用变量n表示,这样式子就是一个反复执行的步骤,因此可以用循环结构实现算法.
要点二:更相减损术
我国早期也有解决求最大公约数问题的算法,就是更相减损术.
更相减损术求最大公约数的步骤如下:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.
翻译出来为:
第一步:任意给出两个正整数;判断它们是否都是偶数.若是,用2约简;若不是,执行第二步.
第二步:以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数.
理论依据:
由,得与有相同的公约数
更相减损术一般算法:
第一步,输入两个正整数;
第二步,如果,则执行,否则转到;
第三步,将的值赋予;
第四步,若,则把赋予,把赋予,否则把赋予,重新执行;
第五步,输出最大公约数.
程序:
INPUT “a=”,a
INPUT “b=”,b
WHILE a<>b
IF a>=b
a=a-b;
ELSE
b=b-a
WEND
END
PRINT b
或者
INPUT “请输入两个不相等的正整数”;a,b
i=0
WHILE a MOD 2=0 AND b MOD 2=0
a=a/2
b=b/2
i=i+1
WEND
DO
IF bt=a
a=b
b=t
END IF
c=a-b
a=b
b=c
LOOP UNTIL a=b
PRINT a^i
END
要点诠释:
用辗转相除法步骤较少,而更相减损术虽然有些步骤较长,但运算简单.
要点三:秦九韶计算多项式的方法
令,则有,其中.这样,我们便可由依次求出;
要点诠释:
显然,用秦九韶算法求n次多项式的值时只需要做n次乘法和n次加法运算
要点四:进位制
进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值.可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n进制.现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数.
对于任何一个数,我们可以用不同的进位制来表示.比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的.
表示各种进位制数一般在数字右下角加注来表示,如111001(2)表示二进制数,34(5)表示5进制数.
1.k进制转换为十进制的方法:
,把k进制数a转化为十进制数b的算法程序为:
INPUT “ a,k,n=”;a,k,n
i=1
b=0
WHILE i<=n
t=GET a[i]
b=b+t*k^(i-1)
i=i+1
WEND
PRINT b
END
2.十进制转化为k进制数b的步骤为:
第一步,将给定的十进制整数除以基数k,余数便是等值的k进制的最低位;
第二步,将上一步的商再除以基数k,余数便是等值的k进制数的次低位;
第三步,重复第二步,直到最后所得的商等于0为止,各次所得的余数,便是k进制各位的数,最后一次余数是最高位,即除k取余法.
要点诠释:
1、在k进制中,具有k个数字符号.如二进制有0,1两个数字.
2、在k进制中,由低位向高位是按“逢k进一”的规则进行计数.
3、非k进制数之间的转化一般应先转化成十进制,再将这个十进制数转化为另一种进制的数,有的也可以相互转化.
【典型例题】
类型一:辗转相除法与更相减损术
例1.分别用辗转相除法和更相减损术求378与90的最大公约数.
【答案】18
【解析】 用辗转相除法:
378=90×4+18,90=18×5.
∴378与90的最大公约数是18.
用更相减损术:
∵378与90都是偶数,
∴用2约分后得189和45.
189-45=144,144-45=99,99-45=54,54-45=9,45-9=36,36-9=27,27-9=18,18-9=9.
∴378与90的最大公约数为2×9=18.
【总结升华】比较辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显;
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.
由该题可以看出,辗转相除法得最大公约数的步骤较少.
对比两种方法控制好算法的结束,辗转相除法是到达余数为0,更相减损术是到达减数和差相等.
举一反三:
【变式1】(1)用更相减损术求两个正数84与72的最大公约数.
(2)利用辗转相除法求3869与6497的最大公约数与最小公倍数.
【解析】 (1) 因为84=21×4,72=18×4,
所以21-18=3,
18-3=15,
15-3=12,
12-3=9,
9-3=6,
6-3=3.
所以21和18的最大公约数等于3.
所以84和72的最大公约数等于12.
【总结升华】先约简,再求21与18的最大公约数,然后乘以约简的4得84与72的最大公约数.
(2)6497=3869×1+2628,
3869=2628×1+1241,
2628=1241×2+146,
1241=146×8+73,
146=73×2+0.
所以3 869与6 497的最大公约数为73,
最小公倍数为3 869×6497÷73=344341.
例2.求三个数:168,54,264的最大公约数.
【思路点拨】运用更相减损术或辗转相除法,先求168和54的最大公约数a,再求a与264的最大公约数.
【答案】6
【解析】
采用更相减损术先求168和54的最大公约数.
(168,54)→(114,54)→(60,54)→(6,54)→(6,48)→(6,42)→(6,36)→(6,30)→(6,24)→(6,18)→(6,12)→(6,6).
故168和54的最大公约数为6.
采用辗转相除法求6和264的最大公约数.
∵264=44×6+0,
∴6为264与6的最大公约数,也是这三个数的最大公约数.
【总结升华】求最大公约数通常有两种方法:一是辗转相除法;二是更相减损术,对于3个数的最大公约数的求法,则是先求其中两个数的最大公约数m,再求m与第三个数的最大公约数.同样可推广到求3个以上数的最大公约数.
举一反三:
【变式1】求三个数324,243,135的最大公约数.
【答案】27
【解析】∵324=243×1+81,
243=81×3+0,
∴324与243的最大公约数为81.
又135=81×1+54,
81=54×1+27,
54=27×2+0,
∴81与135的最大公约数为27.
∴三个数324,243,135的最大公约数为27.
更相减损术:
∵324-243=81,
243-81=162,
162-81=81,
∴81是324和243的最大公约数.
又135-81=54,
81-54=27,
54-27=27,
∴27是81与135的最大公约数.
∴三个数324,243,135的最大公约数为27.
例3.甲、乙、丙三种溶液分别重、、,现要将它们分别全部装入小瓶中,每个小瓶装入液体的质量相同,问每瓶最多装多少?
【思路点拨】由题意,每个小瓶最多能装的溶液的质量应是三种溶液质量的最大公约数.
【答案】
【解析】
先求147与343的最大公约数.
343-147=196,
196-147=49,
147-49=98,
98-49=49,
∴147与343的最大公约数是49.
再求49与133的最大公约数.
133-49=84,
84-49=35,
49-35=14,
35-14=21,
21-14=7,
14-7=7.
∴147,343,133的最大公约数是7.
故每瓶最多装.
【总结升华】本题关键是分析清楚题意,找出三个数的最大公约数.求三个以上(含三个数)的数的最大公约数时,可依次通过求两个数的最大公约数与第三个数的最大公约数来求得.
类型二:秦九韶算法
例4.(2018春 河北邯郸月考)用秦九韶算法求多项式当x=5时的值.
【思路点拨】利用秦九韶算法计算多项式的值,先将多项式转化为的形式,然后逐步计算到的值,即可得到答案.
【答案】2677
【解析】
,
,
,
,
.
所以f(5)=2677.
【总结升华】秦九韶算法的原理是
.
在运用秦九韶算法进行计算时,应注意每一步的运算结果,像这种一环扣一环的运算,如果错一步,则下一步,一直到最后一步就会全部算错.同学们在计算这种题时应格外小心.
举一反三:
【变式1】用秦九韶算法求多项式当x=2时的值.
【答案】1397
【解析】
.
v0=8,
v1=8×2+5=21,
v2=21×2 -0=42,
v3=42×2 -3=87,
v4=87×2+0=174,
v5=174×2+0=348,
v6=348×2+2=698,
v7=698×2+1=1397,
所以,当x=2时,多项式的值为1397.
【变式2】用秦九韶算法计算多项式在x=0.4时的值时,需做加法和乘法的次数和是( )
A.10 B.9 C.12 D.8
【答案】 C
【解析】 .
∴加法6次,乘法6次,
∴6+6=12(次),故选C.
类型三:进位制
例5.(1)试把十进制数136转化为二进制数;
(2)试把十进制数1 234转化为七进制数.
【答案】(1)10001000(2)(2)3412(7)
【解析】 (1)由于136=2×68+0,
68=2×34+0.
34=2×17+0.
17=2×8+1.
8=2×4+0.
4=2×2+0.
2=2×1+0.
1=2×0+1.
所以136=10001000(2).
(2)1234=7×176+2,
176=7×25+1.
25=7×3+4.
3=7×0+3.
所以1234=3412(7).
【总结升华】(1)应注意搞清每一次除法中的被除数、除数,当商为零时停止除法,把每步所得的余数倒着排成一个数,就是相应的二进制数.
(2)十进制数转化为七进制数与转化为二进制数的方法类似,要认真体会其原理.
举一反三:
【变式1】(1)把十进制数89转化为二进制数;
(2)将十进制数2l转化为五进制数.
【解析】(1)用除2取余法:
/
∴89=2×(2×(2×(2×(2×(2×(2×0+1)+0)+1)+1)+0)+0)+1=2×(2×(2×(2×2×(22×0+2+0)+1)+1)+0)+0)+1 =……=1×26+0×25+1×24+1×23+0×22×0×21+1×20=1011001(2)
(2)用除5取余法,可得
/
∴21=41(5).
例6.(2017春 湖南娄底月考)若二进制数100y011和八进制数x03相等,求x+y的值.
【思路点拨】直接利用进位制运算法则化简求解即可.
【答案】1
【解析】,
,
∴67+8y=64x+3,
∵y=0或1,x可以取1、2、3、4、5、6、7,
y=0时,x=1;y=1时,64x=72,无解;
∴x+y=1.
举一反三:
【变式1】在十进制中,,那么在五进制中数码2 004折合成十进制为( )
A.29 B.254 C.602 D.2 004
【答案】B
解析:,故选B.
【变式2】把四进制数2132化为七进制数________.
【答案】314(7)
【解析】先将“四进制”数2132(5)化为十进制数为
然后将十进制的158化为七进制:
158÷7=22余4,
22÷7=3余1,
3÷7=0余3,
所以,结果是314(7)
故答案为:314(7)
【巩固练习】
1.1337与382的最大公约数是( ).
A.3 B.382 C.191 D.201
2.用辗转相除法求得459和357的最大公约数是( ).
A.3 B.9 C.17 D.51
3.下列各数中最小的是( )
A. B. C. D.
4.(2017春 河南灵宝市月考)若用秦九韶算法求多项求当x=3时的值,则需要做乘法运算和加减法运算的次数分别为( )
A.4,2 B.5,3 C.5,2 D.6,2
5.把67转化为二进制数为( ).
A.1100001(2) B.1000011(2) C.110000(2) D.100011l(2)
6.(2018 湖北天门模拟)已知多项式,用秦九韶算法算f(5)时的值为( )
A.22 B.564.9 C.20 D.14130.2
7.已知一个k进制数132与十进制数30相等,那么k等于( ).
A.-7或4 B.-7 C.4 D.都不对
8. 计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制数的对应关系如下表:
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如,用十六进制表示:E+D=1B,则A×B等于( ).
A.6E B.72 C.5F D.B0
9.三个数的最大公约数是 .
10.(2018春 河南期中)若a=111111(2),b=210(6),c=1000(4),d=110(8),则a,b,c,d的大小顺序为________.
11.已知a=333,b=24,则使得a=bq+r(q,r均为自然数,且0≤r<b)成立的q和r的值分别为________.
12. 秦九韶的算法中有个一次式,若令,我们可以得到我们可以利用 结构来实现.
13.(2018春 河北卢龙县期中)用“更相减损术”求(1)中两数的最大公约数,用“辗转相除法”求(2)中两数的最大公约数.用秦九韶算法求函数,当x=3时的函数值.
(1)72,168;
(2)98,280.
14.古时候,当边境有敌人来犯时,守边的官兵通过在烽火台上举火向国内报告,如下图,若烽火台上点火,则用数字1表示,若不点火用数字0表示,约定二进制数对应的十进制数的单位是1000,请你计算一下,这组烽火台表示边境有多少敌人入侵?
/
15.设有甲、乙、丙三种溶液,质量分别为kg、kg、kg.要将它们分别全部装入小瓶中,每个小瓶装入液体的质量相同.每瓶最多装多少?
16.(2017春 甘肃临夏州月考)比较85(9)、210(6)、1000(4)、111111(2)这四个数的大小.
【答案与解析】
1.【答案】C
【解析】 1337=382×3+191,382=191×2+0,1337与382的最大公约数为191.
2.【答案】D
【解析】 ∵459=357×1+102,357=102×3+51,102=51×2+0,即51为459和357的最大公约数.
3.【答案】A
【解析】把这四个数都化为十进制数,,,,故选A.
4.【答案】C
【解析】∵f(x)=((((4x)x)x-1)x)x+2,
∴乘法要运算5次,加减法要运算2次.
故选C.
5.【答案】B
【解析】利用除2取余法易得67=1000011(2).
6.【答案】A
【解析】∵f(x)=((((4x+2)x+3.5)x―2.6)x+1.7)x―0.8,
∴,.
故选:A.
7. 【答案】C
【解析】∵132(k)=1×k2+3k+2=30,∴k=-7或k=4.又∵k>0,∴k=4.故选C.
8. 【答案】A
【解析】A×B用十进制可以表示为10×11=110,而110=6×16+14,所以用十六进制表示为6E,故选A.
9. 【答案】
【解析】
10.【答案】b>d>a>c.
【解析】∵;
;
;
.
∴b>d>a>c.
故答案为:b>d>a>c.
11.【答案】13,21
【解析】 用333除以24,商即为q,余数就是r.333=24×13+21.
12.【答案】;循环
13.【答案】(1)24;(2)14;(3)283
【解析】(1)∵168―72=96,
96―72=24,
72―24=48
48―24=24,
故72和168的最大公约数是24;
(2)∵280=2×98+84,
98=1×84+14,
84=6×14,
故98和280的最大公约数是14;
(3),
当x=3时
,
;
;
;
;
,
即x=3时的函数值为283.
14.【答案】27000
【解析】由题图可知,从左到右的五个烽火台,表示二进制数的自左到右的五个数位.这组烽火台表示的二进制数是11011(2),转化为十进制数为11011(2)=1×24+1×23+0×22+1×21+1×20=16+8+2+1=27.
又27×1000=27000,
所以,这组烽火台表示边境共有27000个敌人入侵.
15.【答案】
【解析】,,.
,,,
,,,
,,,
即与的最大公约数为.
,,,
,,,.
综上所述,、、的最大公约数是.
16.【答案】210(6)>85(9)>1000(4)>111111(2).
【解析】85(9)=8×9+5=77,
,
,
,
故210(6)>85(9)>1000(4)>111111(2).
【学习目标】
1.理解辗转相除法与更相减损术中蕴含的数学原理,并能根据这些原理进行算法分析;
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序;
3.了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质;
4.了解各种进位制与十进制之间转换的规律,会利用各种进位制与十进制之间的联系进行各种进位制之间的转换.
【要点梳理】
要点一:辗转相除法
也叫欧几里德算法,它是由欧几里德在公元前300年左右首先提出的.利用辗转相除法求最大公约数的步骤如下:
第一步:用较大的数m除以较小的数n得到一个商q0和一个余数r0;
第二步:若r0=0,则n为m,n的最大公约数;若r0≠0,则用除数n除以余数r0得到一个商q1和一个余数r1;
第三步:若r1=0,则r0为m,n的最大公约数;若r1≠0,则用除数r0除以余数r1得到一个商q2和一个余数r2;
……
依次计算直至rn=0,此时所得到的rn-1即为所求的最大公约数.
用辗转相除法求最大公约数的程序框图为:
/
程序:
INPUT “m=”;m
INPUT “n=”;n
IF m
m=n
n=x
END IF
r=m MOD n
WHILE r<>0
r=m MOD n
m=n
n=r
WEND
PRINT n
END
要点诠释:
辗转相除法的基本步骤是用较大的数除以较小的数,考虑到算法中的赋值语句可以对同一变量多次赋值,我们可以把较大的数用变量m表示,把较小的数用变量n表示,这样式子就是一个反复执行的步骤,因此可以用循环结构实现算法.
要点二:更相减损术
我国早期也有解决求最大公约数问题的算法,就是更相减损术.
更相减损术求最大公约数的步骤如下:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.
翻译出来为:
第一步:任意给出两个正整数;判断它们是否都是偶数.若是,用2约简;若不是,执行第二步.
第二步:以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数.
理论依据:
由,得与有相同的公约数
更相减损术一般算法:
第一步,输入两个正整数;
第二步,如果,则执行,否则转到;
第三步,将的值赋予;
第四步,若,则把赋予,把赋予,否则把赋予,重新执行;
第五步,输出最大公约数.
程序:
INPUT “a=”,a
INPUT “b=”,b
WHILE a<>b
IF a>=b
a=a-b;
ELSE
b=b-a
WEND
END
PRINT b
或者
INPUT “请输入两个不相等的正整数”;a,b
i=0
WHILE a MOD 2=0 AND b MOD 2=0
a=a/2
b=b/2
i=i+1
WEND
DO
IF bt=a
a=b
b=t
END IF
c=a-b
a=b
b=c
LOOP UNTIL a=b
PRINT a^i
END
要点诠释:
用辗转相除法步骤较少,而更相减损术虽然有些步骤较长,但运算简单.
要点三:秦九韶计算多项式的方法
令,则有,其中.这样,我们便可由依次求出;
要点诠释:
显然,用秦九韶算法求n次多项式的值时只需要做n次乘法和n次加法运算
要点四:进位制
进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值.可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n进制.现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数.
对于任何一个数,我们可以用不同的进位制来表示.比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的.
表示各种进位制数一般在数字右下角加注来表示,如111001(2)表示二进制数,34(5)表示5进制数.
1.k进制转换为十进制的方法:
,把k进制数a转化为十进制数b的算法程序为:
INPUT “ a,k,n=”;a,k,n
i=1
b=0
WHILE i<=n
t=GET a[i]
b=b+t*k^(i-1)
i=i+1
WEND
PRINT b
END
2.十进制转化为k进制数b的步骤为:
第一步,将给定的十进制整数除以基数k,余数便是等值的k进制的最低位;
第二步,将上一步的商再除以基数k,余数便是等值的k进制数的次低位;
第三步,重复第二步,直到最后所得的商等于0为止,各次所得的余数,便是k进制各位的数,最后一次余数是最高位,即除k取余法.
要点诠释:
1、在k进制中,具有k个数字符号.如二进制有0,1两个数字.
2、在k进制中,由低位向高位是按“逢k进一”的规则进行计数.
3、非k进制数之间的转化一般应先转化成十进制,再将这个十进制数转化为另一种进制的数,有的也可以相互转化.
【典型例题】
类型一:辗转相除法与更相减损术
例1.分别用辗转相除法和更相减损术求378与90的最大公约数.
【答案】18
【解析】 用辗转相除法:
378=90×4+18,90=18×5.
∴378与90的最大公约数是18.
用更相减损术:
∵378与90都是偶数,
∴用2约分后得189和45.
189-45=144,144-45=99,99-45=54,54-45=9,45-9=36,36-9=27,27-9=18,18-9=9.
∴378与90的最大公约数为2×9=18.
【总结升华】比较辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显;
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.
由该题可以看出,辗转相除法得最大公约数的步骤较少.
对比两种方法控制好算法的结束,辗转相除法是到达余数为0,更相减损术是到达减数和差相等.
举一反三:
【变式1】(1)用更相减损术求两个正数84与72的最大公约数.
(2)利用辗转相除法求3869与6497的最大公约数与最小公倍数.
【解析】 (1) 因为84=21×4,72=18×4,
所以21-18=3,
18-3=15,
15-3=12,
12-3=9,
9-3=6,
6-3=3.
所以21和18的最大公约数等于3.
所以84和72的最大公约数等于12.
【总结升华】先约简,再求21与18的最大公约数,然后乘以约简的4得84与72的最大公约数.
(2)6497=3869×1+2628,
3869=2628×1+1241,
2628=1241×2+146,
1241=146×8+73,
146=73×2+0.
所以3 869与6 497的最大公约数为73,
最小公倍数为3 869×6497÷73=344341.
例2.求三个数:168,54,264的最大公约数.
【思路点拨】运用更相减损术或辗转相除法,先求168和54的最大公约数a,再求a与264的最大公约数.
【答案】6
【解析】
采用更相减损术先求168和54的最大公约数.
(168,54)→(114,54)→(60,54)→(6,54)→(6,48)→(6,42)→(6,36)→(6,30)→(6,24)→(6,18)→(6,12)→(6,6).
故168和54的最大公约数为6.
采用辗转相除法求6和264的最大公约数.
∵264=44×6+0,
∴6为264与6的最大公约数,也是这三个数的最大公约数.
【总结升华】求最大公约数通常有两种方法:一是辗转相除法;二是更相减损术,对于3个数的最大公约数的求法,则是先求其中两个数的最大公约数m,再求m与第三个数的最大公约数.同样可推广到求3个以上数的最大公约数.
举一反三:
【变式1】求三个数324,243,135的最大公约数.
【答案】27
【解析】∵324=243×1+81,
243=81×3+0,
∴324与243的最大公约数为81.
又135=81×1+54,
81=54×1+27,
54=27×2+0,
∴81与135的最大公约数为27.
∴三个数324,243,135的最大公约数为27.
更相减损术:
∵324-243=81,
243-81=162,
162-81=81,
∴81是324和243的最大公约数.
又135-81=54,
81-54=27,
54-27=27,
∴27是81与135的最大公约数.
∴三个数324,243,135的最大公约数为27.
例3.甲、乙、丙三种溶液分别重、、,现要将它们分别全部装入小瓶中,每个小瓶装入液体的质量相同,问每瓶最多装多少?
【思路点拨】由题意,每个小瓶最多能装的溶液的质量应是三种溶液质量的最大公约数.
【答案】
【解析】
先求147与343的最大公约数.
343-147=196,
196-147=49,
147-49=98,
98-49=49,
∴147与343的最大公约数是49.
再求49与133的最大公约数.
133-49=84,
84-49=35,
49-35=14,
35-14=21,
21-14=7,
14-7=7.
∴147,343,133的最大公约数是7.
故每瓶最多装.
【总结升华】本题关键是分析清楚题意,找出三个数的最大公约数.求三个以上(含三个数)的数的最大公约数时,可依次通过求两个数的最大公约数与第三个数的最大公约数来求得.
类型二:秦九韶算法
例4.(2018春 河北邯郸月考)用秦九韶算法求多项式当x=5时的值.
【思路点拨】利用秦九韶算法计算多项式的值,先将多项式转化为的形式,然后逐步计算到的值,即可得到答案.
【答案】2677
【解析】
,
,
,
,
.
所以f(5)=2677.
【总结升华】秦九韶算法的原理是
.
在运用秦九韶算法进行计算时,应注意每一步的运算结果,像这种一环扣一环的运算,如果错一步,则下一步,一直到最后一步就会全部算错.同学们在计算这种题时应格外小心.
举一反三:
【变式1】用秦九韶算法求多项式当x=2时的值.
【答案】1397
【解析】
.
v0=8,
v1=8×2+5=21,
v2=21×2 -0=42,
v3=42×2 -3=87,
v4=87×2+0=174,
v5=174×2+0=348,
v6=348×2+2=698,
v7=698×2+1=1397,
所以,当x=2时,多项式的值为1397.
【变式2】用秦九韶算法计算多项式在x=0.4时的值时,需做加法和乘法的次数和是( )
A.10 B.9 C.12 D.8
【答案】 C
【解析】 .
∴加法6次,乘法6次,
∴6+6=12(次),故选C.
类型三:进位制
例5.(1)试把十进制数136转化为二进制数;
(2)试把十进制数1 234转化为七进制数.
【答案】(1)10001000(2)(2)3412(7)
【解析】 (1)由于136=2×68+0,
68=2×34+0.
34=2×17+0.
17=2×8+1.
8=2×4+0.
4=2×2+0.
2=2×1+0.
1=2×0+1.
所以136=10001000(2).
(2)1234=7×176+2,
176=7×25+1.
25=7×3+4.
3=7×0+3.
所以1234=3412(7).
【总结升华】(1)应注意搞清每一次除法中的被除数、除数,当商为零时停止除法,把每步所得的余数倒着排成一个数,就是相应的二进制数.
(2)十进制数转化为七进制数与转化为二进制数的方法类似,要认真体会其原理.
举一反三:
【变式1】(1)把十进制数89转化为二进制数;
(2)将十进制数2l转化为五进制数.
【解析】(1)用除2取余法:
/
∴89=2×(2×(2×(2×(2×(2×(2×0+1)+0)+1)+1)+0)+0)+1=2×(2×(2×(2×2×(22×0+2+0)+1)+1)+0)+0)+1 =……=1×26+0×25+1×24+1×23+0×22×0×21+1×20=1011001(2)
(2)用除5取余法,可得
/
∴21=41(5).
例6.(2017春 湖南娄底月考)若二进制数100y011和八进制数x03相等,求x+y的值.
【思路点拨】直接利用进位制运算法则化简求解即可.
【答案】1
【解析】,
,
∴67+8y=64x+3,
∵y=0或1,x可以取1、2、3、4、5、6、7,
y=0时,x=1;y=1时,64x=72,无解;
∴x+y=1.
举一反三:
【变式1】在十进制中,,那么在五进制中数码2 004折合成十进制为( )
A.29 B.254 C.602 D.2 004
【答案】B
解析:,故选B.
【变式2】把四进制数2132化为七进制数________.
【答案】314(7)
【解析】先将“四进制”数2132(5)化为十进制数为
然后将十进制的158化为七进制:
158÷7=22余4,
22÷7=3余1,
3÷7=0余3,
所以,结果是314(7)
故答案为:314(7)
【巩固练习】
1.1337与382的最大公约数是( ).
A.3 B.382 C.191 D.201
2.用辗转相除法求得459和357的最大公约数是( ).
A.3 B.9 C.17 D.51
3.下列各数中最小的是( )
A. B. C. D.
4.(2017春 河南灵宝市月考)若用秦九韶算法求多项求当x=3时的值,则需要做乘法运算和加减法运算的次数分别为( )
A.4,2 B.5,3 C.5,2 D.6,2
5.把67转化为二进制数为( ).
A.1100001(2) B.1000011(2) C.110000(2) D.100011l(2)
6.(2018 湖北天门模拟)已知多项式,用秦九韶算法算f(5)时的值为( )
A.22 B.564.9 C.20 D.14130.2
7.已知一个k进制数132与十进制数30相等,那么k等于( ).
A.-7或4 B.-7 C.4 D.都不对
8. 计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制数的对应关系如下表:
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如,用十六进制表示:E+D=1B,则A×B等于( ).
A.6E B.72 C.5F D.B0
9.三个数的最大公约数是 .
10.(2018春 河南期中)若a=111111(2),b=210(6),c=1000(4),d=110(8),则a,b,c,d的大小顺序为________.
11.已知a=333,b=24,则使得a=bq+r(q,r均为自然数,且0≤r<b)成立的q和r的值分别为________.
12. 秦九韶的算法中有个一次式,若令,我们可以得到我们可以利用 结构来实现.
13.(2018春 河北卢龙县期中)用“更相减损术”求(1)中两数的最大公约数,用“辗转相除法”求(2)中两数的最大公约数.用秦九韶算法求函数,当x=3时的函数值.
(1)72,168;
(2)98,280.
14.古时候,当边境有敌人来犯时,守边的官兵通过在烽火台上举火向国内报告,如下图,若烽火台上点火,则用数字1表示,若不点火用数字0表示,约定二进制数对应的十进制数的单位是1000,请你计算一下,这组烽火台表示边境有多少敌人入侵?
/
15.设有甲、乙、丙三种溶液,质量分别为kg、kg、kg.要将它们分别全部装入小瓶中,每个小瓶装入液体的质量相同.每瓶最多装多少?
16.(2017春 甘肃临夏州月考)比较85(9)、210(6)、1000(4)、111111(2)这四个数的大小.
【答案与解析】
1.【答案】C
【解析】 1337=382×3+191,382=191×2+0,1337与382的最大公约数为191.
2.【答案】D
【解析】 ∵459=357×1+102,357=102×3+51,102=51×2+0,即51为459和357的最大公约数.
3.【答案】A
【解析】把这四个数都化为十进制数,,,,故选A.
4.【答案】C
【解析】∵f(x)=((((4x)x)x-1)x)x+2,
∴乘法要运算5次,加减法要运算2次.
故选C.
5.【答案】B
【解析】利用除2取余法易得67=1000011(2).
6.【答案】A
【解析】∵f(x)=((((4x+2)x+3.5)x―2.6)x+1.7)x―0.8,
∴,.
故选:A.
7. 【答案】C
【解析】∵132(k)=1×k2+3k+2=30,∴k=-7或k=4.又∵k>0,∴k=4.故选C.
8. 【答案】A
【解析】A×B用十进制可以表示为10×11=110,而110=6×16+14,所以用十六进制表示为6E,故选A.
9. 【答案】
【解析】
10.【答案】b>d>a>c.
【解析】∵;
;
;
.
∴b>d>a>c.
故答案为:b>d>a>c.
11.【答案】13,21
【解析】 用333除以24,商即为q,余数就是r.333=24×13+21.
12.【答案】;循环
13.【答案】(1)24;(2)14;(3)283
【解析】(1)∵168―72=96,
96―72=24,
72―24=48
48―24=24,
故72和168的最大公约数是24;
(2)∵280=2×98+84,
98=1×84+14,
84=6×14,
故98和280的最大公约数是14;
(3),
当x=3时
,
;
;
;
;
,
即x=3时的函数值为283.
14.【答案】27000
【解析】由题图可知,从左到右的五个烽火台,表示二进制数的自左到右的五个数位.这组烽火台表示的二进制数是11011(2),转化为十进制数为11011(2)=1×24+1×23+0×22+1×21+1×20=16+8+2+1=27.
又27×1000=27000,
所以,这组烽火台表示边境共有27000个敌人入侵.
15.【答案】
【解析】,,.
,,,
,,,
,,,
即与的最大公约数为.
,,,
,,,.
综上所述,、、的最大公约数是.
16.【答案】210(6)>85(9)>1000(4)>111111(2).
【解析】85(9)=8×9+5=77,
,
,
,
故210(6)>85(9)>1000(4)>111111(2).
