人教A版数学选修2—1 2.3.2 双曲线的简单几何性质第一课时
文档属性
| 名称 | 人教A版数学选修2—1 2.3.2 双曲线的简单几何性质第一课时 |
|
|
| 格式 | zip | ||
| 文件大小 | 238.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-14 11:09:51 | ||
图片预览




文档简介
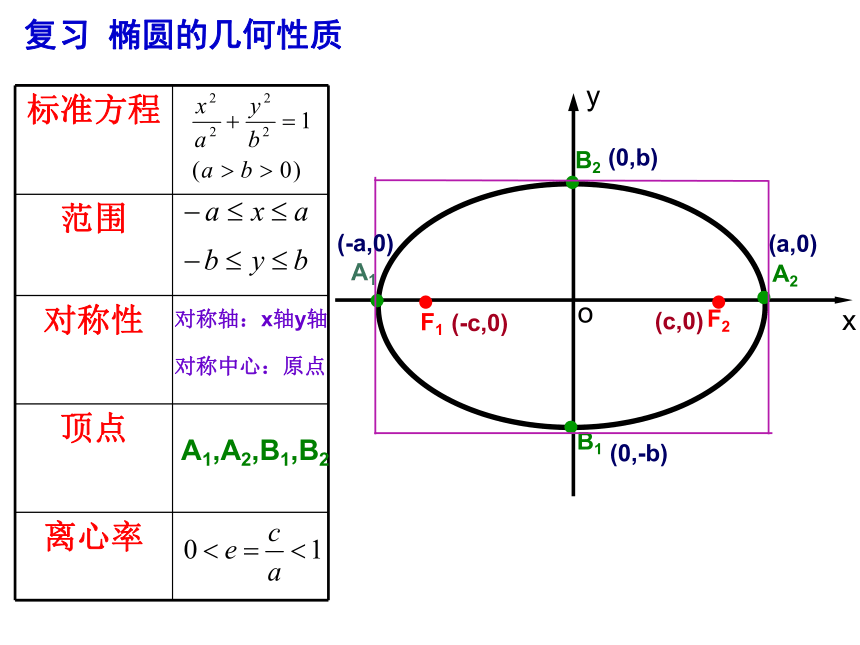
课件15张PPT。 2.3.2双曲线
的简单几何性质思考:
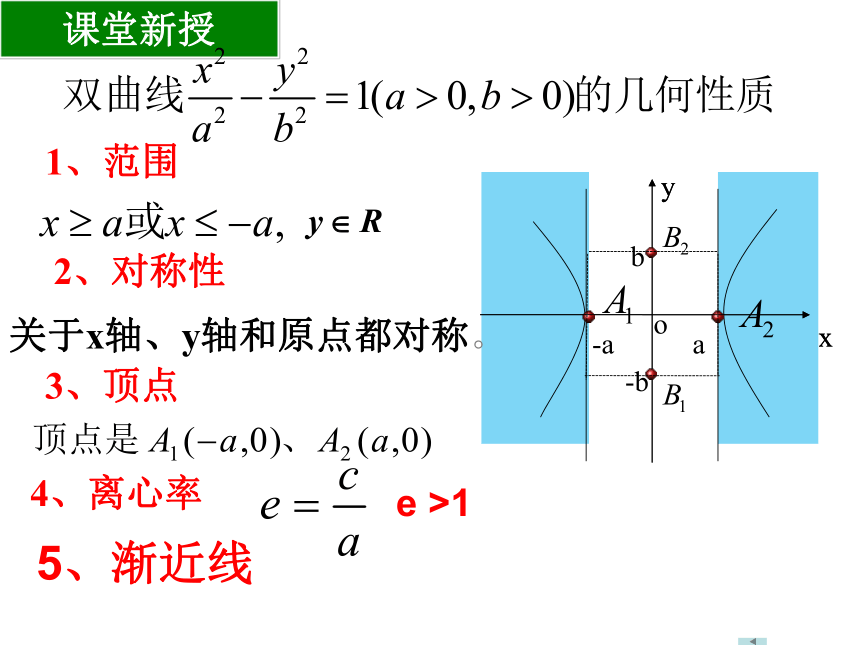
焦点在x轴上的椭圆的几何性质有哪些?
(从范围,对称性,顶点,离心率四个方面说明)学习目标:
?知识与技能:知道双曲线的几何性质,能根据性质
解决一些基本问题培养学生分析,归纳,推理的能力.
?过程与方法:与椭圆的性质类比中获得双曲线的
性质,进一步体会数形结合思想,掌握利用方程研究
曲线性质的方法.
?情感态度与价值观:通过类比的方法探索新知识,
培养学生学习数学的兴趣.
oyxF1F2A1A2B2B1复习 椭圆的几何性质对称轴:x轴y轴对称中心:原点A1,A2,B1,B2(-c,0)(c,0)(-a,0)(a,0)(0,-b)(0,b) 2、对称性 1、范围关于x轴、y轴和原点都对称。xy课堂新授 3、顶点4、离心率e >15、渐近线 双曲线的渐近线思考:
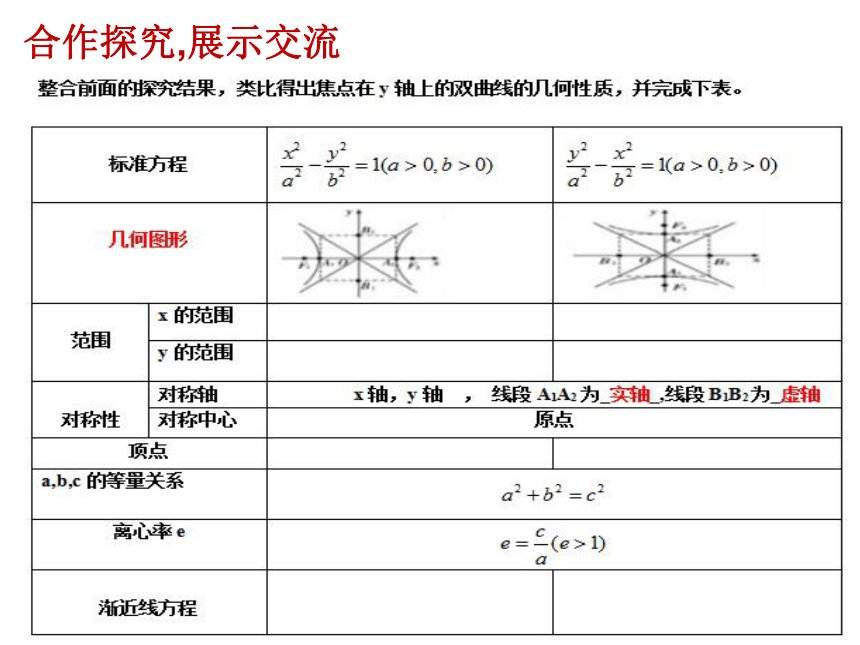
类比焦点在x轴上的双曲线的
几何性质,那么当焦点在y轴上
的双曲线的几何性质是什么?
请完成下面的表格(学案上).合作探究,展示交流
④离心率可以刻画椭圆的扁平程度,离心率e的变化对双曲线图形有什么影响?
①双曲线的焦点能在虚轴上吗?②双曲线的顶点就是双曲线与坐标轴的交点,
你认为对吗?③等轴双曲线的定义及离心率是什么?思考 A1(-a,0) , A2(a,0) ,
B1(0,b) , B2(0,-b) x ≥a 或 x ≤ -a对称轴:x轴,y轴
对称中心:原点A1(-a,0 ) 、A2(a,0)a2=c2-b2e=c/a e>1a2=b2+c2e=c/a 0对称中心:原点椭圆与双曲线的比较例题分析,拓展延伸解:拓展延伸:本节课我们学习了那些知识点?yF2B1A2A1B2 0xF1X=aX=-a yx oA2A1 B1B2F1 F2渐近线方程 双曲线的渐近线B1A2A1B2 0xF1X=aX=-a课后作业:
的简单几何性质思考:
焦点在x轴上的椭圆的几何性质有哪些?
(从范围,对称性,顶点,离心率四个方面说明)学习目标:
?知识与技能:知道双曲线的几何性质,能根据性质
解决一些基本问题培养学生分析,归纳,推理的能力.
?过程与方法:与椭圆的性质类比中获得双曲线的
性质,进一步体会数形结合思想,掌握利用方程研究
曲线性质的方法.
?情感态度与价值观:通过类比的方法探索新知识,
培养学生学习数学的兴趣.
oyxF1F2A1A2B2B1复习 椭圆的几何性质对称轴:x轴y轴对称中心:原点A1,A2,B1,B2(-c,0)(c,0)(-a,0)(a,0)(0,-b)(0,b) 2、对称性 1、范围关于x轴、y轴和原点都对称。xy课堂新授 3、顶点4、离心率e >15、渐近线 双曲线的渐近线思考:
类比焦点在x轴上的双曲线的
几何性质,那么当焦点在y轴上
的双曲线的几何性质是什么?
请完成下面的表格(学案上).合作探究,展示交流
④离心率可以刻画椭圆的扁平程度,离心率e的变化对双曲线图形有什么影响?
①双曲线的焦点能在虚轴上吗?②双曲线的顶点就是双曲线与坐标轴的交点,
你认为对吗?③等轴双曲线的定义及离心率是什么?思考 A1(-a,0) , A2(a,0) ,
B1(0,b) , B2(0,-b) x ≥a 或 x ≤ -a对称轴:x轴,y轴
对称中心:原点A1(-a,0 ) 、A2(a,0)a2=c2-b2e=c/a e>1a2=b2+c2e=c/a 0
