人教A版数学必修4 1.4.1 正弦函数、余弦函数的图象(共15张ppt)
文档属性
| 名称 | 人教A版数学必修4 1.4.1 正弦函数、余弦函数的图象(共15张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 740.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-14 00:00:00 | ||
图片预览



文档简介
课件15张PPT。1.4.1 正弦函数、余弦函数的图象 三角函数三角函数线正弦函数
复习:
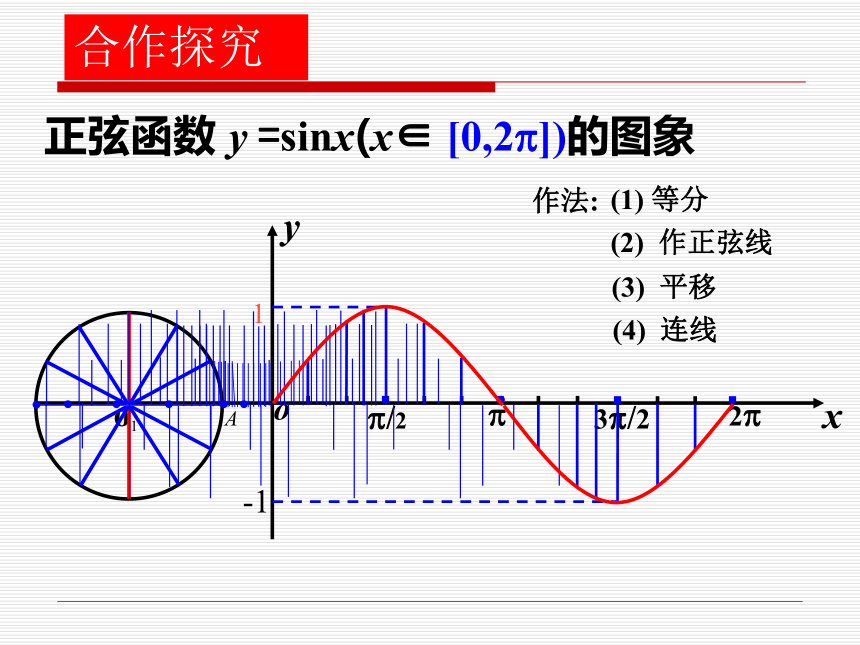
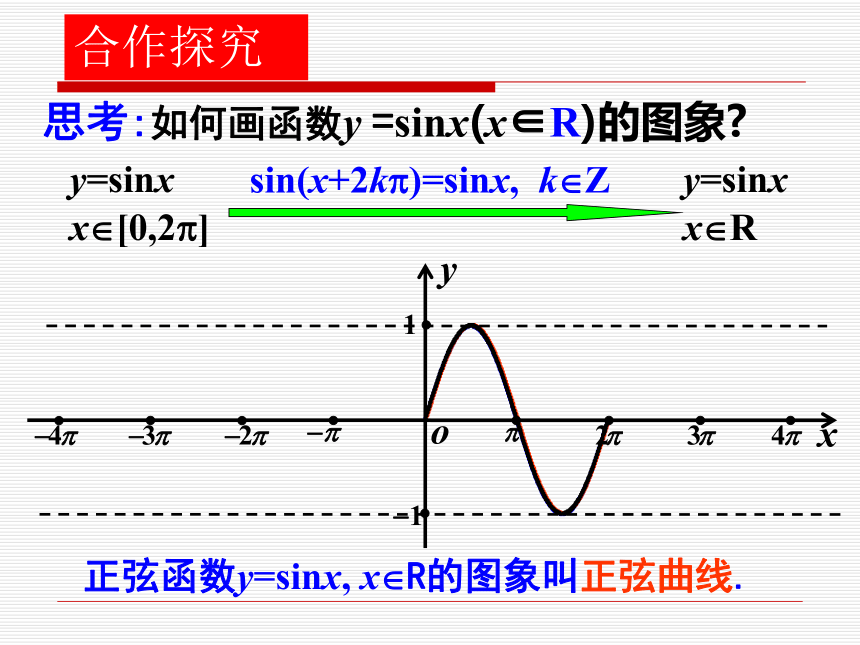
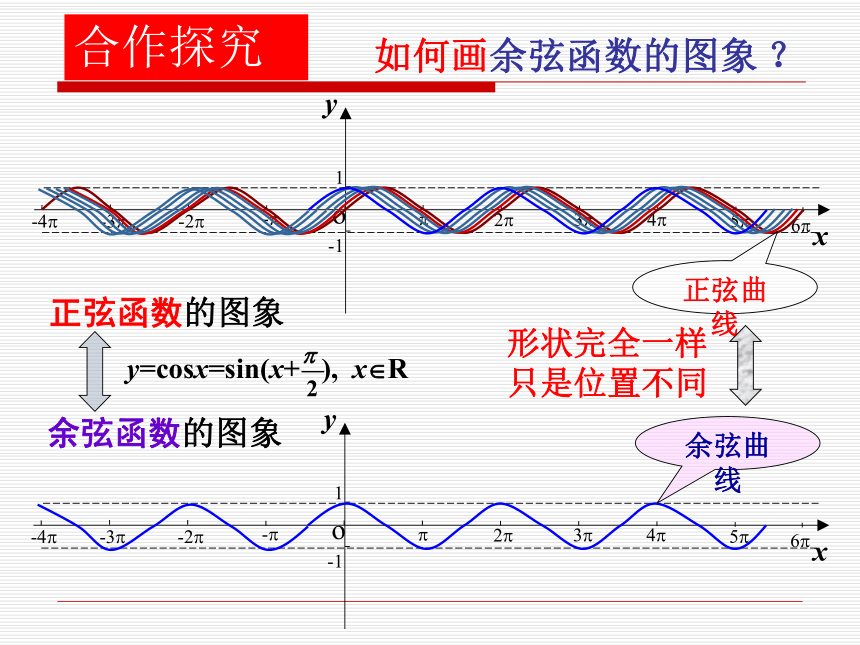
1.在单位圆中,角?的正弦线、余弦线、正切线分别是什么??PMsin?=MP正弦线MP如何在直角坐标系中作出点 OPMxy.思考:正弦函数 y =sinx(x∈ [0,2?])的图象o1A.......作法:(1) 等分(2) 作正弦线(3) 平移(4) 连线合作探究 思考:如何画函数y =sinx(x∈R)的图象?y=sinx x?[0,2?]y=sinx x?Rsin(x+2k?)=sinx, k?Z正弦函数y=sinx, x?R的图象叫正弦曲线.合作探究 如何画余弦函数的图象 ?余弦函数的图象 正弦函数的图象 y=cosx=sin(x+ ), x?R余弦曲线正弦曲线形状完全一样只是位置不同合作探究 在精确度要求不太高时,如何快捷地作出正弦函数的图象呢?
在作出正弦函数的图象时,应抓住哪些
关键点?思考图象与x轴的交点图象的最高点图象的最低点图象中关键点五点法作图?简图作法(“五点法”作图)
①列表(列出对图象形状起关键作用的五点坐标)
②描点(定出五个关键点)
③连线(用光滑的曲线顺次连结五个点)五点法作图1-1(1) 列表(2) 描点(3) 连线请你试试用五点法画出函数
的图象.余弦函数的“五点法作图”01-101描点作图10-101-1010-1思考:能否从图象变换的角度出发得到(1)(2)的图象?典型举例 0 ? 2 ?思考题 在同一坐标系内,用五点法分别画出函数
y= sinx,x?[0, 2?] 和 y= cosx,x?[ , ]的简图:y=sinx,x?[0, 2?]y= cosx,x?[ , ] 向左平移 个单位长度100-10 0 ? 1. 正弦曲线、余弦曲线作法2.正弦曲线和余弦曲线之间的区别与联系;小结 (1)查找单位圆中的三角函数线和三角函数的图象资料.
(2)预习1.4.2作业
复习:
1.在单位圆中,角?的正弦线、余弦线、正切线分别是什么??PMsin?=MP正弦线MP如何在直角坐标系中作出点 OPMxy.思考:正弦函数 y =sinx(x∈ [0,2?])的图象o1A.......作法:(1) 等分(2) 作正弦线(3) 平移(4) 连线合作探究 思考:如何画函数y =sinx(x∈R)的图象?y=sinx x?[0,2?]y=sinx x?Rsin(x+2k?)=sinx, k?Z正弦函数y=sinx, x?R的图象叫正弦曲线.合作探究 如何画余弦函数的图象 ?余弦函数的图象 正弦函数的图象 y=cosx=sin(x+ ), x?R余弦曲线正弦曲线形状完全一样只是位置不同合作探究 在精确度要求不太高时,如何快捷地作出正弦函数的图象呢?
在作出正弦函数的图象时,应抓住哪些
关键点?思考图象与x轴的交点图象的最高点图象的最低点图象中关键点五点法作图?简图作法(“五点法”作图)
①列表(列出对图象形状起关键作用的五点坐标)
②描点(定出五个关键点)
③连线(用光滑的曲线顺次连结五个点)五点法作图1-1(1) 列表(2) 描点(3) 连线请你试试用五点法画出函数
的图象.余弦函数的“五点法作图”01-101描点作图10-101-1010-1思考:能否从图象变换的角度出发得到(1)(2)的图象?典型举例 0 ? 2 ?思考题 在同一坐标系内,用五点法分别画出函数
y= sinx,x?[0, 2?] 和 y= cosx,x?[ , ]的简图:y=sinx,x?[0, 2?]y= cosx,x?[ , ] 向左平移 个单位长度100-10 0 ? 1. 正弦曲线、余弦曲线作法2.正弦曲线和余弦曲线之间的区别与联系;小结 (1)查找单位圆中的三角函数线和三角函数的图象资料.
(2)预习1.4.2作业
