人教A版数学必修4 2.1 平面向量的实际背景及基本概念(共30张ppt)
文档属性
| 名称 | 人教A版数学必修4 2.1 平面向量的实际背景及基本概念(共30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-14 11:17:15 | ||
图片预览








文档简介
课件30张PPT。平面向量的实际背景及基本概念1.掌握向量的意义、表示方法以及有关概念.
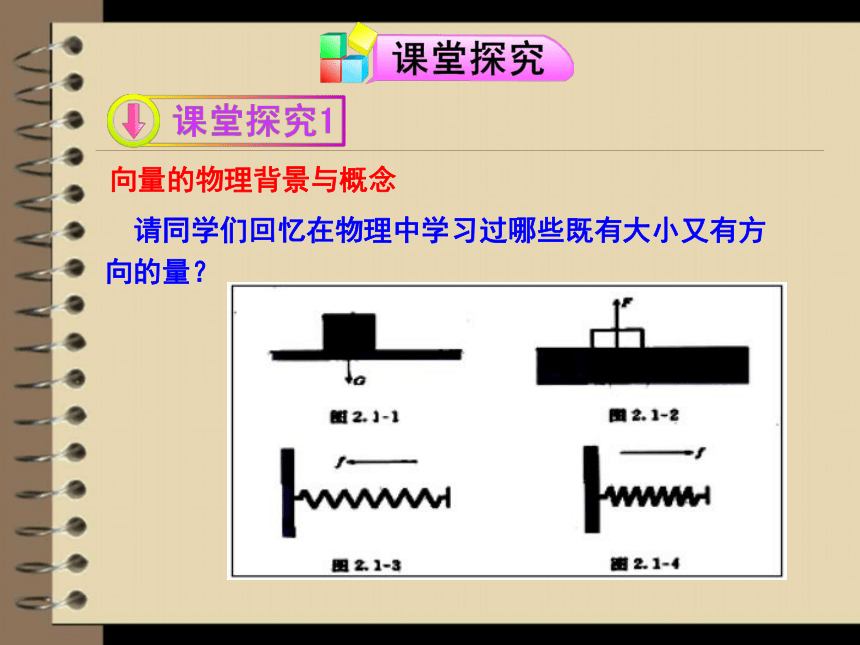
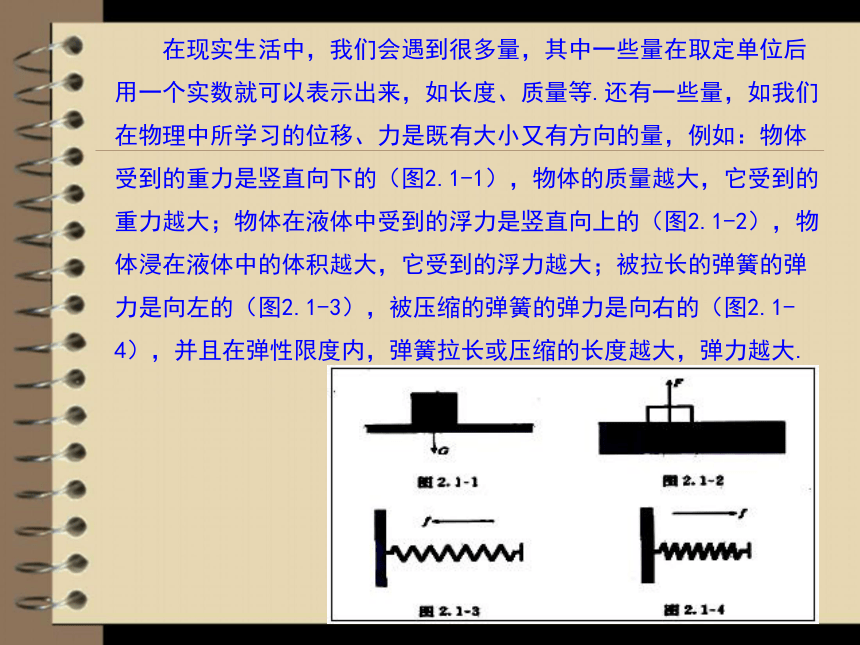
2.能作一个向量与已知向量相等,根据图形判定向量是否平行. 同学们都知道,数学是一门基础学科,是解决其它一些学科问题的有力工具.其实数学的很多理论是由其它学科的一些知识抽象而来的.成为理论后又反过来对其它学科起作用.比如同学们学习的物理,它与数学就有非常密切的关系.唉, 哪儿去了?嘻嘻!大笨猫!AB老鼠由A向东北方向以每秒6米的速度逃窜,如果猫由B向正东方向以每秒10米速度追赶,那么猫能否抓到老鼠?为什么?2.1平面向量的实际背景 及基本概念 请同学们回忆在物理中学习过哪些既有大小又有方向的量? 向量的物理背景与概念 在现实生活中,我们会遇到很多量,其中一些量在取定单位后用一个实数就可以表示出来,如长度、质量等.还有一些量,如我们在物理中所学习的位移、力是既有大小又有方向的量,例如:物体受到的重力是竖直向下的(图2.1-1),物体的质量越大,它受到的重力越大;物体在液体中受到的浮力是竖直向上的(图2.1-2),物体浸在液体中的体积越大,它受到的浮力越大;被拉长的弹簧的弹力是向左的(图2.1-3),被压缩的弹簧的弹力是向右的(图2.1-4),并且在弹性限度内,弹簧拉长或压缩的长度越大,弹力越大.一、向量的定义既有大小,又有方向的量叫做向量.数量只有大小,可以进行代数运算、比较大小;向量有方向,大小,不能比较大小.思考:年龄,身高,面积,体积,质量是向量吗?为什么?
二、向量的表示方法有向线段 (起点、 )(1)几何表示法: a ,b,(2)字母表示法: 方向、长度问题:“向量就是有向线段,有向线段就是向量.”的说
法对吗?不对,①向量只有大小和方向两个要素;与起点无关:只要大小和方向相同,则这两个向量就是相同的向量;②有向线段有起点、大小和方向三个要素,起点不同,尽管大小和方向相同,也是不同的有向线段.三、向量的有关概念1.向量的长度(模):向量AB的大小,也就是向量 的长度(或称模). |AB|记作2.两个特殊向量: 问:在平面上把所有单位向量的起点平移到同一点P,那么它们的终点的集合组成什么图形?零向量---长度为0的向量叫做零向量,记作 0.单位向量---长度等于1个单位的向量叫作单位向量. 数学中的向量与起点无关,用有向线段表示向量时,起点可以取任意位置。
所以,数学中的向量也叫自由向量。特别提示:四、向量间的关系各向量的终点与直线l之间有什么关系?问:把一组平行于直线l的向量的起点平移到直线l上的一点O ,这时它们是不是平行向量?Ol .扎实认真 勤学苦练 例1.如图,试根据图中的比例尺以及三地的位置,在图中分别用向量表示A地至B、C两地的位移,并求出A地至B、C两地的实际距离(精确到1km). 200km . 表示A地至C地的位移,且 280km .【解析】: 表示A地至B地的位移,且【变式训练1】在某次军事演习中,红方一支装甲分队为完成对蓝军的穿插包围,先从A处出发向西迂回了100 km到达B地,然后又改变方向向北偏西40°走了200 km到达C地,最后又改变方向,向东突进100 km到达D处,完成了对蓝军的包围.
(1)作出向量
(2)求出【审题指导】作图时既要考虑向量的大小,又要考虑其方向及起点,为此可建立平面直角坐标系,在坐标系中作图求解.【规范解答】(1)向量 如图所示: (2)由题意,例2.如图,设O是正六边形ABCDEF的中心,分别写出图中与 平行的向量.
【解析】:方向相同
或相反判断下列说法的正误.
①向量 与 是平行向量,则向量 与 不是平行向量;
②单位向量都相同;
③任一向量与它的相反向量(长度相同,方向相反的向量)不相等;(×)(×)(×)同学们:再努力一下,你就成功了!【能力1】下列说法正确的是( )
(A)若 ∥ ,则 与 的方向相同或相反
(B)若 ∥ , ∥ ,则 ∥
(C)若两个单位向量平行,则这两个单位向量相同
(D)若两个向量相同,则这两个向量平行
【审题指导】解决此类问题的主要依据是相关概念.利用平行向量、单位向量的概念逐个判断.【答案】选D.【能力2】零向量与单位向量的关系是______(填“平行”、“垂直”、“无关”).
【解析】由于我们规定:零向量与任何向量平行,所以零向量与单位向量“垂直”、“无关”是错误的.
答案:平行【能力3】如图,以1×2方格纸中的格点(各线段的交点)为起点和终点的向量中,
(1)写出与 平行的向量;
(2)写出与 模相等的向量.
【解析】(1)与 平行的向量为
与 平行的向量为
(2)与 模相等的向量
零向量、单位向量的概念: 平行向量的定义.
2.能作一个向量与已知向量相等,根据图形判定向量是否平行. 同学们都知道,数学是一门基础学科,是解决其它一些学科问题的有力工具.其实数学的很多理论是由其它学科的一些知识抽象而来的.成为理论后又反过来对其它学科起作用.比如同学们学习的物理,它与数学就有非常密切的关系.唉, 哪儿去了?嘻嘻!大笨猫!AB老鼠由A向东北方向以每秒6米的速度逃窜,如果猫由B向正东方向以每秒10米速度追赶,那么猫能否抓到老鼠?为什么?2.1平面向量的实际背景 及基本概念 请同学们回忆在物理中学习过哪些既有大小又有方向的量? 向量的物理背景与概念 在现实生活中,我们会遇到很多量,其中一些量在取定单位后用一个实数就可以表示出来,如长度、质量等.还有一些量,如我们在物理中所学习的位移、力是既有大小又有方向的量,例如:物体受到的重力是竖直向下的(图2.1-1),物体的质量越大,它受到的重力越大;物体在液体中受到的浮力是竖直向上的(图2.1-2),物体浸在液体中的体积越大,它受到的浮力越大;被拉长的弹簧的弹力是向左的(图2.1-3),被压缩的弹簧的弹力是向右的(图2.1-4),并且在弹性限度内,弹簧拉长或压缩的长度越大,弹力越大.一、向量的定义既有大小,又有方向的量叫做向量.数量只有大小,可以进行代数运算、比较大小;向量有方向,大小,不能比较大小.思考:年龄,身高,面积,体积,质量是向量吗?为什么?
二、向量的表示方法有向线段 (起点、 )(1)几何表示法: a ,b,(2)字母表示法: 方向、长度问题:“向量就是有向线段,有向线段就是向量.”的说
法对吗?不对,①向量只有大小和方向两个要素;与起点无关:只要大小和方向相同,则这两个向量就是相同的向量;②有向线段有起点、大小和方向三个要素,起点不同,尽管大小和方向相同,也是不同的有向线段.三、向量的有关概念1.向量的长度(模):向量AB的大小,也就是向量 的长度(或称模). |AB|记作2.两个特殊向量: 问:在平面上把所有单位向量的起点平移到同一点P,那么它们的终点的集合组成什么图形?零向量---长度为0的向量叫做零向量,记作 0.单位向量---长度等于1个单位的向量叫作单位向量. 数学中的向量与起点无关,用有向线段表示向量时,起点可以取任意位置。
所以,数学中的向量也叫自由向量。特别提示:四、向量间的关系各向量的终点与直线l之间有什么关系?问:把一组平行于直线l的向量的起点平移到直线l上的一点O ,这时它们是不是平行向量?Ol .扎实认真 勤学苦练 例1.如图,试根据图中的比例尺以及三地的位置,在图中分别用向量表示A地至B、C两地的位移,并求出A地至B、C两地的实际距离(精确到1km). 200km . 表示A地至C地的位移,且 280km .【解析】: 表示A地至B地的位移,且【变式训练1】在某次军事演习中,红方一支装甲分队为完成对蓝军的穿插包围,先从A处出发向西迂回了100 km到达B地,然后又改变方向向北偏西40°走了200 km到达C地,最后又改变方向,向东突进100 km到达D处,完成了对蓝军的包围.
(1)作出向量
(2)求出【审题指导】作图时既要考虑向量的大小,又要考虑其方向及起点,为此可建立平面直角坐标系,在坐标系中作图求解.【规范解答】(1)向量 如图所示: (2)由题意,例2.如图,设O是正六边形ABCDEF的中心,分别写出图中与 平行的向量.
【解析】:方向相同
或相反判断下列说法的正误.
①向量 与 是平行向量,则向量 与 不是平行向量;
②单位向量都相同;
③任一向量与它的相反向量(长度相同,方向相反的向量)不相等;(×)(×)(×)同学们:再努力一下,你就成功了!【能力1】下列说法正确的是( )
(A)若 ∥ ,则 与 的方向相同或相反
(B)若 ∥ , ∥ ,则 ∥
(C)若两个单位向量平行,则这两个单位向量相同
(D)若两个向量相同,则这两个向量平行
【审题指导】解决此类问题的主要依据是相关概念.利用平行向量、单位向量的概念逐个判断.【答案】选D.【能力2】零向量与单位向量的关系是______(填“平行”、“垂直”、“无关”).
【解析】由于我们规定:零向量与任何向量平行,所以零向量与单位向量“垂直”、“无关”是错误的.
答案:平行【能力3】如图,以1×2方格纸中的格点(各线段的交点)为起点和终点的向量中,
(1)写出与 平行的向量;
(2)写出与 模相等的向量.
【解析】(1)与 平行的向量为
与 平行的向量为
(2)与 模相等的向量
零向量、单位向量的概念: 平行向量的定义.
