五年级数学下册4.4正方体长方体的表面积教案沪教版
文档属性
| 名称 | 五年级数学下册4.4正方体长方体的表面积教案沪教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 135.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-13 21:57:57 | ||
图片预览


文档简介
正方体、长方体的表面积
【教学目标】
[认知目标]:
知道物体外部所有面的总面积叫做它的表面积。
能正确计算正方体和长方体的表面积。
[能力目标]
让学生自主探究正方体和长方体表面积的计算方法。
[情感目标]
通过实际的操作过程,体验学习的快乐。
【教学重点】
掌握与理解正方体、长方体表面积的含义及计算表面积的方法。
【教学难点】
正方体、长方体表面积的推导过程。
【教学准备】
教学课件、长方体、正方体的附页等。
【教学过程】
复习导入:
正方形的面积计算公式是什么?
板书:正方形的面积
S = a2
请学生观察老师手中的正方体,回答问题?
(1)正方体有几个面?
(2)有什么特征?
(3)如何计算它们的面积?
这节课让我们学习有关求正方体面积的知识。
揭示课题:正方体的面积
【说明:让学生回忆有关正方体特征的知识,承上启下引导出本堂课的学习内容,激发学生学习的积极性。】
探究新知:
正方体的表面积。
小胖将一个棱成为5厘米的正方体盒子沿着棱切开,得到一个正方体表面的展开图。
先仔细观察正方体表面的展开图,然后回答问题?
正方体表面的展开图是由六个什么形状的面组成的?
这六个面的形状都相同吗?
面积都相等吗?
面积的总和是多少?
这个正方体表面的展开图有6个正方形的面,它们的形状都相同,面积都相等。
面积的总和 = 6 × ( 棱成 × 棱长)
= 6 ×( 5 × 5)
= 150( cm3)
正方体有六个大小相同的正方形面,六个面的面积总和称为正方体的表面积。
小结。
【说明:充分让学生通过已有的知识和经验,小组合作,主动探究求正方体的表面积。】
练一练:
求下面正方体的表面积?
正方体的棱长为6dm,求它的表面积。
解: S = 6 a2
=6×6×6
=216(cm2)
答:它的表面积是216平方厘米。
正方体的棱成为7cm,求它的表面积。
探一探,练一练:
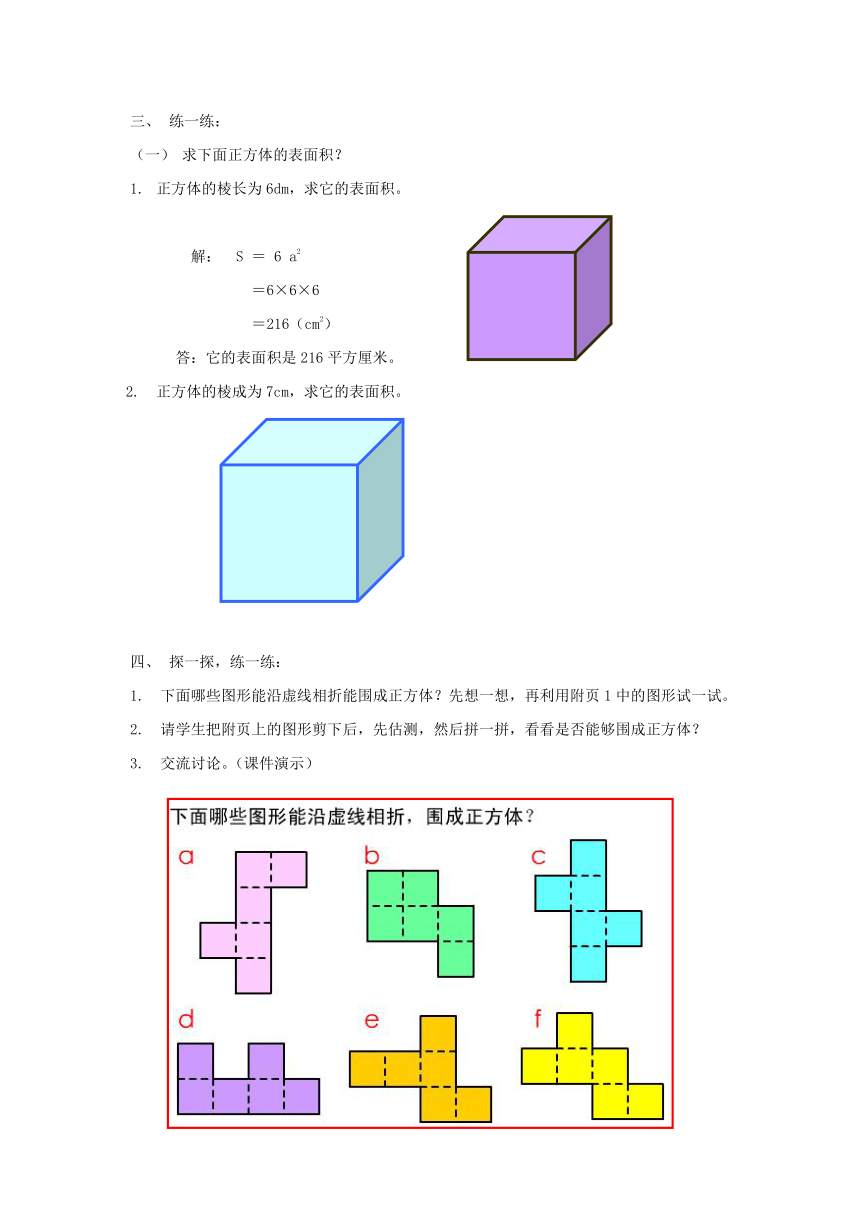
下面哪些图形能沿虚线相折能围成正方体?先想一想,再利用附页1中的图形试一试。
请学生把附页上的图形剪下后,先估测,然后拼一拼,看看是否能够围成正方体?
交流讨论。(课件演示)
其中:a、c、e、f这四幅能够拼成正方体。
b和d的图形不能拼成正方体。
小亚用1立方厘米的正方体积木搭出了一个棱长为3厘米的正方体,并且将它的表面涂上了红色。
三面涂上红色的1立方厘米的正方体积木有多少个?
两面涂上红色的1立方厘米的正方体积木有多少个?
一面涂上红色的1立方厘米的正方体积木有多少个?
没有面涂上红色的1立方厘米的正方体积木有多少个?
学生讨论交流,请学生可以用小正方体搭一搭,找出规律。
利用课件反馈。
小结。
【说明:这里的正方体的展开图并不是这一节的重点,只是为了能帮助学生推导出表面积,并相应地积累空间经验,并在思路上能从“立体”——“平面”——“立体”。第4题计数时要讲究策略:三面有颜色的在八个角上,共8块;两面有颜色的在各条棱上,每条棱上只有1块,共12块;一面有颜色的在6个面的中心,共6块;没有颜色的,只有1块,在“中心”。】
巩固练习:
看图练习:
下面的正方体的棱长为5m,先求它的表面积,再求体积。
下面正方体的棱长为0.7dm,先求它的表面积,再求体积。
下面图形中哪些能围成正方体?哪些不能围成正方体?
拓展小练习:
正方体的表面积是96平方厘米,它的一个面的面积是多少平方厘米?它的棱长是多少厘米?
做一个棱长为7dm的正方体无盖木盒,需要多少平方分米的木板?
用一根长60厘米的铁丝,围成一个正方体的小铁筐,在外面贴上手工纸,需要多少平方厘米的手工纸?它的体积是多少?
用3块棱长为3厘米的小正方体拼成一个长方体,面积减少多少平方厘米?
做一个正方体的玻璃金鱼缸,棱长为80厘米,需要多少平方厘米的玻璃?
正方体的棱长是6cm,它的表面积和体积相比较,情况怎样?
一个棱长为4厘米的正方体,在它的角上挖掉一块棱成为2厘米的小正方体(如下图),它的表面积发生了什么变化?是增加、减少、相等还是无法确定?
小结。
【说明:通过练一练和拓展小练习,让学生进一步巩固求正方体表面积的计算方法。】
总结:
师:说说今天我们学习了什么知识,发现了什么,对我们有何帮助?你对你今天的学习评价如何?
a2
a2
a2
a2
a2
a2
a
a
a
