黑龙江大庆市万宝学校(五四制)2018-2019学年八年级下学期期末考试数学试题(Word版含答案)
文档属性
| 名称 | 黑龙江大庆市万宝学校(五四制)2018-2019学年八年级下学期期末考试数学试题(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 264.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-14 13:43:57 | ||
图片预览



文档简介
大庆市万宝学校2018-2019学年下学期八年级期末考试
数学试题
考生注意:1、考试时间:120分钟
2、全卷共 27 道小题,满分 120
选择题(每小题3分,共计30分)
1.已知关于x的方程x2-kx-6=0的一个根为x=3,则实数k的值为( ???)
A.1 B. C.2 D.
2.一元二次方程x=2x的根是 ( )
A.x=0
B.x=2
C.x =0,x=2
D.无实数根
3.在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是( )
A.
B.
C.
D.
4.下列四幅图形中,表示两颗小树在同一时刻阳光下的影子的图形可能是( )
5.已知反比例函数,在每个象限内y随着x的增大而增大,点P(a-1, 2)在这个反比例函数上,a的值可以是(???)
A.0 B.1 C.2 D.3
6.如图,在菱形ABCD中,DE⊥AB,,BE=2,则tan∠DBE的值是(??? )
B.2 C. D.
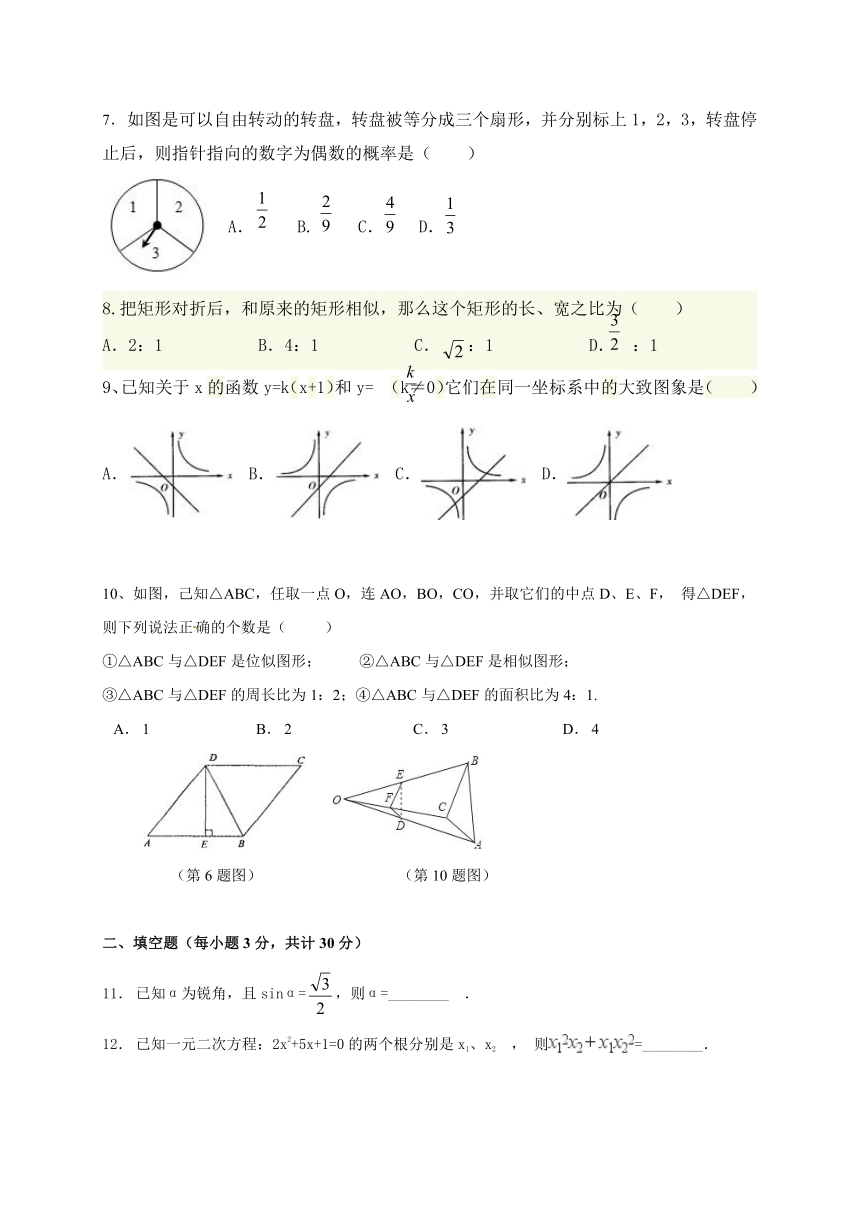
7.如图是可以自由转动的转盘,转盘被等分成三个扇形,并分别标上1,2,3,转盘停止后,则指针指向的数字为偶数的概率是( ) A. B. C. D.
8.把矩形对折后,和原来的矩形相似,那么这个矩形的长、宽之比为(? )
A.2:1????? B.4:1????? C.:1????? D. :1
9、已知关于x的函数y=k(x+1)和y= (k≠0)它们在同一坐标系中的大致图象是( )
A.
B.
C.
D.
10、如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D、E、F, 得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形;? ? ②△ABC与△DEF是相似图形; ③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
A.1 B.2 C.3 D.4
(第6题图) (第10题图)
二、填空题(每小题3分,共计30分)
11.已知α为锐角,且sinα=,则α=________?.
12.已知一元二次方程:2x2+5x+1=0的两个根分别是x1、x2 , 则=________.
13.已知(﹣1,y1)(﹣2,y2)(, y3)都在反比例函数y=﹣的图象上,则y1 、y2 、 y3的大小关系是________ .
14.如图,小芳和爸爸正在散步,爸爸身高1.8m,他在地面上的影长为2.1m,若小芳比爸爸矮0.3m,则她的影长为
15..在△ABC中,若∠A、∠B满足|cosA- |+(sinB- )2=0,则∠C=
16.如图,正比例函数y=ax的图象与反比例函数y=的图象相交于点A,B,若点A的坐标为(﹣2,3),则点B的坐标为________?
(第16题图) (第17题图) (第18题图)
17.如图,点A在双曲线y= 上,AB⊥y轴于B,S△ABO =3,则k=
18.若干桶方便面摆放在桌子上,实物图片左边所给的是它的三视图,则这一堆方便面共有_______桶。
19.如图,C为线段AB上的一点,△ACM、△CBN都是等边三角形,若AC=3,BC=2,则△MCD与△BND的面积比为
20.如图,在Rt△ABC中,AC=8,BC=6,直线l经过C,且l∥AB,P为l上一个动点,若△ABC与△PAC相似,则PC=________?
(第19题图) (第20题图)
三、解答题(共计60分)
21.(8分)(1)解方程:x2+3x-4=0 (2) 计算:
22.(8分)如图,在△ABC中,D为AC边上一点,∠DBC=∠A. (1)求证:△BDC∽△ABC; (2)如果BC=, AC=3,求CD的长. ?
23.(8分)一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有任何其他区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取出红球的概率是
(1)取出白球的概率是多少? (2)如果袋中的白球有18只,那么袋中的红球有多少只?
24.(8分)如图,在平行四边形中,E是AB延长线上的一点,DE交BC于点F.已知 ,,求△CDF的面积.
(8分)钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10海里,求AC的距离.(结果保留根号)
26.(8分)如图,已知A(﹣4,n),B(1,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.、(1)求△AOB的面积;(2)求不等式kx+b﹣<0的解集(请直接写出答案).
27.(12分)如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y= 的图象在第一象限内的交点为M,若△OBM的面积为1.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
大庆市万宝学校2018-2019学年上学期八年级期末考试答案
填空题
1—5 ACADA 6-10 BDCCC
填空题 11、60° 12、 13、 14、1.75m 15、75° 16、(2,-3) 17、6 18、6 19、9:4 20、10或6.4
解答题
(1) (2)
(1)证明:∵∠DBC=∠A
∠DCB=∠BAC????
∴△ACD∽△ABC?.? -
(2)解:∵△ACD∽△ABC
∴BC:AC=CD:BC?????? -
∵BC=,AC=3
∴CD=2来.????????????????
1.=?
2.设袋中的红球有只,则有
???(或)???????
解得?????????????????????????????
所以,袋中的红球有6只.
24.、
.25.解:作BD⊥AC交AC的延长线于D, 由题意得,∠BCD=45°,BC=10海里, ∴CD=BD=10海里, ∵AB=20海里,BD=10海里, ∴AD= =10, ∴AC=AD﹣CD=10﹣10海里. 答:AC的距离为(10﹣10)海里.
26..解:(1)∵反比例函数y=(m≠0)过点B(1,﹣4), ∴m=1×(﹣4)=﹣4, ∴y=﹣, 将x=﹣4,y=n代入反比例解析式得:n=1, ∴A(﹣4,1), ∴将A与B坐标代入一次函数解析式得:, 解得:, ∴y=﹣x﹣3; 在直线y=﹣x﹣3中,当y=0时,x=﹣3, ∴C(﹣3,0),即OC=3, ∴S△AOB=S△AOC+S△COB=(3×1+3×4)=; (2)不等式kx+b﹣<0的解集是﹣4<x<0或x>1.
数学试题
考生注意:1、考试时间:120分钟
2、全卷共 27 道小题,满分 120
选择题(每小题3分,共计30分)
1.已知关于x的方程x2-kx-6=0的一个根为x=3,则实数k的值为( ???)
A.1 B. C.2 D.
2.一元二次方程x=2x的根是 ( )
A.x=0
B.x=2
C.x =0,x=2
D.无实数根
3.在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是( )
A.
B.
C.
D.
4.下列四幅图形中,表示两颗小树在同一时刻阳光下的影子的图形可能是( )
5.已知反比例函数,在每个象限内y随着x的增大而增大,点P(a-1, 2)在这个反比例函数上,a的值可以是(???)
A.0 B.1 C.2 D.3
6.如图,在菱形ABCD中,DE⊥AB,,BE=2,则tan∠DBE的值是(??? )
B.2 C. D.
7.如图是可以自由转动的转盘,转盘被等分成三个扇形,并分别标上1,2,3,转盘停止后,则指针指向的数字为偶数的概率是( ) A. B. C. D.
8.把矩形对折后,和原来的矩形相似,那么这个矩形的长、宽之比为(? )
A.2:1????? B.4:1????? C.:1????? D. :1
9、已知关于x的函数y=k(x+1)和y= (k≠0)它们在同一坐标系中的大致图象是( )
A.
B.
C.
D.
10、如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D、E、F, 得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形;? ? ②△ABC与△DEF是相似图形; ③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
A.1 B.2 C.3 D.4
(第6题图) (第10题图)
二、填空题(每小题3分,共计30分)
11.已知α为锐角,且sinα=,则α=________?.
12.已知一元二次方程:2x2+5x+1=0的两个根分别是x1、x2 , 则=________.
13.已知(﹣1,y1)(﹣2,y2)(, y3)都在反比例函数y=﹣的图象上,则y1 、y2 、 y3的大小关系是________ .
14.如图,小芳和爸爸正在散步,爸爸身高1.8m,他在地面上的影长为2.1m,若小芳比爸爸矮0.3m,则她的影长为
15..在△ABC中,若∠A、∠B满足|cosA- |+(sinB- )2=0,则∠C=
16.如图,正比例函数y=ax的图象与反比例函数y=的图象相交于点A,B,若点A的坐标为(﹣2,3),则点B的坐标为________?
(第16题图) (第17题图) (第18题图)
17.如图,点A在双曲线y= 上,AB⊥y轴于B,S△ABO =3,则k=
18.若干桶方便面摆放在桌子上,实物图片左边所给的是它的三视图,则这一堆方便面共有_______桶。
19.如图,C为线段AB上的一点,△ACM、△CBN都是等边三角形,若AC=3,BC=2,则△MCD与△BND的面积比为
20.如图,在Rt△ABC中,AC=8,BC=6,直线l经过C,且l∥AB,P为l上一个动点,若△ABC与△PAC相似,则PC=________?
(第19题图) (第20题图)
三、解答题(共计60分)
21.(8分)(1)解方程:x2+3x-4=0 (2) 计算:
22.(8分)如图,在△ABC中,D为AC边上一点,∠DBC=∠A. (1)求证:△BDC∽△ABC; (2)如果BC=, AC=3,求CD的长. ?
23.(8分)一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有任何其他区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取出红球的概率是
(1)取出白球的概率是多少? (2)如果袋中的白球有18只,那么袋中的红球有多少只?
24.(8分)如图,在平行四边形中,E是AB延长线上的一点,DE交BC于点F.已知 ,,求△CDF的面积.
(8分)钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10海里,求AC的距离.(结果保留根号)
26.(8分)如图,已知A(﹣4,n),B(1,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.、(1)求△AOB的面积;(2)求不等式kx+b﹣<0的解集(请直接写出答案).
27.(12分)如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y= 的图象在第一象限内的交点为M,若△OBM的面积为1.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
大庆市万宝学校2018-2019学年上学期八年级期末考试答案
填空题
1—5 ACADA 6-10 BDCCC
填空题 11、60° 12、 13、 14、1.75m 15、75° 16、(2,-3) 17、6 18、6 19、9:4 20、10或6.4
解答题
(1) (2)
(1)证明:∵∠DBC=∠A
∠DCB=∠BAC????
∴△ACD∽△ABC?.? -
(2)解:∵△ACD∽△ABC
∴BC:AC=CD:BC?????? -
∵BC=,AC=3
∴CD=2来.????????????????
1.=?
2.设袋中的红球有只,则有
???(或)???????
解得?????????????????????????????
所以,袋中的红球有6只.
24.、
.25.解:作BD⊥AC交AC的延长线于D, 由题意得,∠BCD=45°,BC=10海里, ∴CD=BD=10海里, ∵AB=20海里,BD=10海里, ∴AD= =10, ∴AC=AD﹣CD=10﹣10海里. 答:AC的距离为(10﹣10)海里.
26..解:(1)∵反比例函数y=(m≠0)过点B(1,﹣4), ∴m=1×(﹣4)=﹣4, ∴y=﹣, 将x=﹣4,y=n代入反比例解析式得:n=1, ∴A(﹣4,1), ∴将A与B坐标代入一次函数解析式得:, 解得:, ∴y=﹣x﹣3; 在直线y=﹣x﹣3中,当y=0时,x=﹣3, ∴C(﹣3,0),即OC=3, ∴S△AOB=S△AOC+S△COB=(3×1+3×4)=; (2)不等式kx+b﹣<0的解集是﹣4<x<0或x>1.
同课章节目录
