人教版高中数学必修5同步练习题、期中、期末复习资料、补习资料:06【基础】正余弦定理在解三角形中的应用
文档属性
| 名称 | 人教版高中数学必修5同步练习题、期中、期末复习资料、补习资料:06【基础】正余弦定理在解三角形中的应用 |  | |
| 格式 | zip | ||
| 文件大小 | 454.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-30 11:09:38 | ||
图片预览




文档简介
正弦、余弦定理在三角形中的应用
【学习目标】
1.进一步巩固正弦定理和余弦定理,并能综合运用两个定理解决三角形的有关问题;
2.学会用方程思想解决有关三角形的问题,提高综合运用知识的能力和解题的优化意识.
【要点梳理】
要点一、正弦定理和余弦定理的概念
①正弦定理公式:
(其中R表示三角形的外接圆半径)
②余弦定理公式:
第一形式:
第二形式:
要点二、三角形的面积公式
① ;
②;
要点三、利用正、余弦定理解三角形
已知两边和一边的对角或已知两角及一边时,通常选择正弦定理来解三角形;已知两边及夹角或已知三边时,通常选择余弦定理来解三角形.特别是求角时尽量用余弦定理来求,尽量避免分类讨论.
在中,已知和A时,解的情况主要有以下几类:
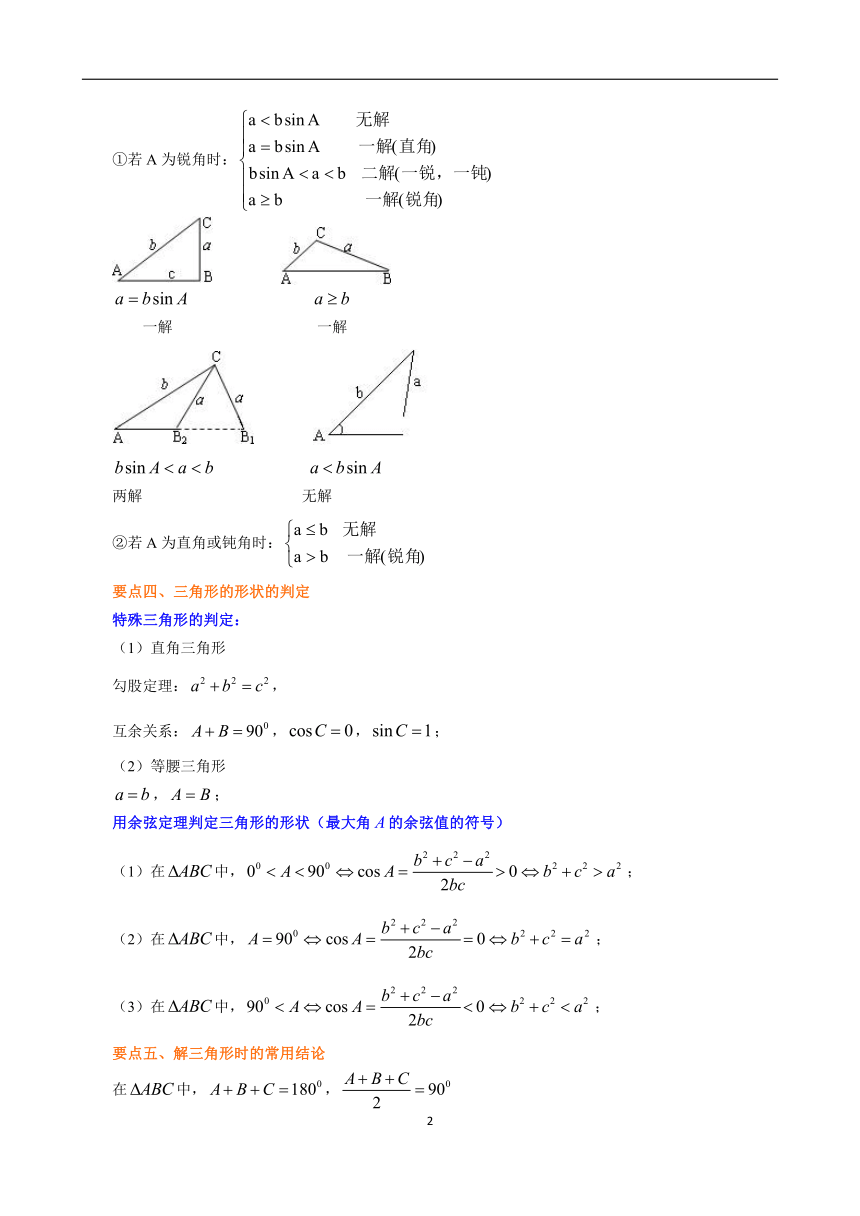
①若A为锐角时:
/ /
一解 一解
/ /
两解 无解
②若A为直角或钝角时:
要点四、三角形的形状的判定
特殊三角形的判定:
(1)直角三角形
勾股定理:,
互余关系:,,;
(2)等腰三角形
,;
用余弦定理判定三角形的形状(最大角的余弦值的符号)
(1)在中,;
(2)在中,;
(3)在中,;
要点五、解三角形时的常用结论
在中,,
(1)在中
(2)互补关系:,
,
;
(3)互余关系:,
,
.
【典型例题】
类型一:利用正、余弦定理解三角形
例1. 在中,已知下列条件,解三角形.
(1), , ;
(2),,.
【思路点拨】
(1)题中利用正弦定理先求,再求和;
(2)题中利用余弦定理求;求可以利用余弦定理,也可以利用正弦定理。
【解析】
(1)∵,
法一:∵,∴,即,
∴,,.
法二:∵, ∴或,
①当时,,;
②当时,(舍去).
(2)∵
∴
法一:∵
∴,
法二:∵
又∵,即
∴,有,
∴,.
【总结升华】
①解三角形时,可以依据题意画出恰当的示意图,然后正确选择正、余弦定理解答;
②解三角形时,要留意三角形内角和为180°、同一个三角形中大边对大角等性质的应用。
举一反三:
【变式1】 △ABC中,已知c=1,b=,∠B=45°,求∠C和a.
【答案】∵,(舍)
或由正弦定理得:.
【变式2】在中, 求角;
【答案】.
【变式3】在中,若,,,求角和.
【答案】根据余弦定理:,
∵,
∴,。
例2、(2018 浙江)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知/.
(1)求tanC的值;
(2)若△ABC的面积为3,求b的值。
【答案】(1)2;(2)3.
【思路分析】(1)根据正弦定理可将条件中的边之间的关系转化为角之间满足的关系,再将式子作三角恒等变形即可求解;(2)根据条件首先求得sinB的值,再结合正弦定理以及三角形面积的计算公式即可求解.
【解析】(1)由及正弦定理得,∴-cos2B=sin2C,
又由,即,得-cos2B=sin2C=2sinCcosC,解得tanC=2;
(2)由tanC=2,C∈(0,π)得,
又,由正弦定理得,
又,故b=3.
【总结升华】
对于求解三角形的题目,一般都可有两种思路:边化角或角化成边,但要根据结论的形式选择转成边或者角。
举一反三:
【变式】△ABC中,A=45°,a=2,求b和B,C.
【答案】
解法一 :正弦定理
由
若C=60°,则B=75°,
若C=120°,则B=15°,
解法二:余弦定理
若
若
解法三:正余弦定理
若
∵b>c>a,所以B>C>A,所以B=75°,C=60°;
若
∵c>a>b,所以C>A>B,所以B=15°,C=120°.
类型二:正、余弦定理的综合应用
例3.已知△ABC 中,试判断△ABC的形状.
【思路点拨】
题目中给的是角与边的混合关系式,可用正弦定理化简成单一的角的关系;也可以用正弦定理、余弦定理化简成单一的边的关系,然后判断.
【解析】
方法一:用余弦定理化角为边的关系
由得,
整理得,
即,
当时,为等腰三角形;
当即时,则为直角三角形;
综上:为等腰或直角三角形。
方法二:用正弦定理化边为角的关系
由正弦定理得:
即,
∵,
∴
即
∵
∴或,即或
故为等腰三角形或直角三角形。
【总结升华】
(1)要判断三角形的形状特征,必须深入研究边与边的大小关系:是否两边相等?是否三边相等?是否符合勾股定理?还要研究角与角的大小关系:是否两个角相等?是否三个角相等?有无直角或钝角?
(2)解题的思想方法是:从条件出发,利用正、余弦定理等进行代换、转化、化简、运算,找出边与边的关系或角与角的关系,从而作出正确判断。
(3)一般有两种转化方向:要么转化为边,要么转化为角。
(4)判断三角形形状时,用边做、用角做均可。一般地,题目中给的是角,就用角做;题目中给的是边,就用边做,边角之间的转换可用正弦定理或余弦定理。
(5),不要丢解。
举一反三:
【变式1】根据下列条件,试判断△ABC的形状.
(1)bcosA=acosB;(2)a=2bcosC
【答案】
(1)解法一:正弦定理
由bcosA=acosB得2RsinBcosA=2RsinAcosB,
即sin(B-A)=0,于是B=A,
∴△ABC为等腰三角形.
解法二:余弦定理
由bcosA=acosB得,即a2=b2,
所以a=b,△ABC为等腰三角形.
(2)解法一:正弦定理
由a=2bcosC得2RsinA=4RsinBcosC,有sin(B+C)=2sinBcosC,得出sin(B-C)=0,
即B=C,△ABC为等腰三角形;
解法二:余弦定理
由a=2bcosC得,得b2=c2,
即b=c,△ABC等腰三角形.
【变式2】在△ABC中,根据下列条件决定三角形形状.
(1);(2).
【答案】
(1)由
,
则该三角形为直角三角形;
(2)∵,
∴,
由正弦定理得:,
∵中,, ,
∴,即,
∴或,即:或,
∴是等腰三角形或直角三角形.
例4. (2017 四川理)在△ABC中,角A,B,C所对的边分别是a,b,c,且.
(I)证明:;
(II)若,求.
【答案】(I)略(II)4
【思路点拨】第一问,利用正弦定理,将边角进行转化,结合诱导公式进行证明;第二问,利用余弦定理解出,在根据平方关系解出,代入已知中,解出的值。
【解析】(I)根据正弦定理,可设
则
代入中,有
,变形可得
在中,由 ,有
所以
(II)由已知,,根据余弦定理,有
由(),
所以
故
举一反三:
【变式】(2017 天津文)在中,内角所对应的边分别为a,b,c,已知.
(Ⅰ)求B;
(Ⅱ)若,求sinC的值.
【答案】(Ⅰ)在中,由,可得,又由得
,
所以 得
(Ⅱ)由得 则,
所以
例5.锐角 中,a,b,c分别是角A,B,C的对边。
若求的大小
取最大值时,求的大小
【思路点拨】在(1)中,将所给边的关系式化简变形后,根据结构形式可判断出应该用余弦定理。
【解析】(1)∵, ∴,
故由余弦定理得
∵A是锐角三角形的内角,所以
∴
(2)=
当且仅当时取等号
∴
【总结升华】
对于三角形中边角的最大值或最小值问题可以运用正弦定理或余弦定理建立所求变量与三角形的角或边之间的函数关系,利用正、余弦函数的有界性或二次函数的知识解决问题
举一反三:
【变式1】已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)(sinA-sinB)=(c-b)sinC,则△ABC面积的最大值为 .
答案:
解析:∵△ABC中, a=2,且(2+b)(sinA-sinB)=(c-b)sinC,
∴利用正弦定理可得 4-b2=(c-b)c,即 b2+c2-bc=4.
再利用基本不等式可得 4≥2bc-bc=bc,∴bc≤4,当且仅当b=c=2时,取等号,
此时,△ABC为等边三角形,它的面积为bc·sinA=,
故答案为:.
【变式2】在中,三内角满足的方程
有两个相等的根。
求证:角B不大于
(2)当角B取最大值时,判断的形状
【答案】
(1)由韦达定理得即,
由正弦定理,有2b=a+c
由余弦定理得
∴
(2)当角B取最大值时,,且a=c,易知为正三角形
【巩固练习】
一、选择题
1.(2017 新课标Ⅲ理)在/中,/,BC边上的高等于/,则/( )
A./ B./ C./ D./
2.中,若,则有( )
A. B. C. D.、大小不能确定
3.在△ABC中,若a=7,b=3,c=8,则△ABC的面积等于( )
A.12 B.
C.28 D.
4.边长为的三角形的最大角与最小角的和是( )
A. B. C. D.
5.钝角三角形ABC的面积是,AB=1,BC=,则AC=( )
A. 5 B. C. 2 D. 1
二、填空题
6. 在中,已知,则的度数为 .
7. (2017 新课标Ⅱ理) /的内角/的对边分别为/,若/,/,/,则/ .
8.在△ABC中,A=60°,AC=4,BC=,则△ABC的面积等于 .
9. 在△ABC中,角A,B,C所对应的边分别为a,b,c,已知bcosC+ccosB=2b,则= .
10. 锐角△ABC的面积为,BC=4,CA=3,则AB=________.
11.在△ABC中,三边a,b,c与面积S的关系式为a2+4S=b2+c2,则角A为________.
三、解答题
12.已知a=3/,c=2,B=150°,求边b的长及S△.
13.(2018 江苏)在△ABC中,已知AB=2,AC=3,A=60°.
(1)求BC的长;
(2)求sin2C的值.
14. 已知的三角内角、、有2B=A+C,三边、、满足.
求证:.
15. (2017 浙江理)在△ABC中,内角A,B,C所对的边分别为a,b,c. 已知b+c=2a cos B.
(I)证明:A=2B;
(II)若△ABC的面积,求角A的大小.
【答案与解析】
1. 答案: C
解析:设/边上的高线为/,则/,所以/,/.由余弦定理,知/,故选C.
2. 答案: C
解析:∵,∴由正弦定理有,
即,整理得
即, ∴
3答案: D
.解析: 由余弦定理可得cos A=,A=60°,∴S△ABC=bcsin A
=.故选D.
4. 答案:B
解析: 设中间角为,则为所求
5. 答案:B
解析:∵钝角三角形ABC的面积是,AB=c=1,BC=a=,
∴S=acsinB=,即sinB=,
当B为钝角时,cosB=-=-,
利用余弦定理得:AC2=AB2+BC2-2AB?BC?cosB=1+2+2=5,即AC=,
当B为锐角时,cosB==,
利用余弦定理得:AC2=AB2+BC2-2AB?BC?cosB=1+2-2=1,即AC=1,
此时AB2+AC2=BC2,即△ABC为直角三角形,不合题意,舍去,
则AC=.
故选:B.
6.解析:∵,∴,
∴,∴
7.解析:∵ ,且为三角形内角,所以
= ,又因为 所以
.
8. 答案:.
解析:∵△ABC中,A=60°,AC=4,BC=,
由正弦定理得:,
∴,解得sinB=1,
∴B=90°,C=30°,
∴△ABC的面积=
故答案为:.
9. 答案:2
解析:将bcosC+ccosB=2b,利用正弦定理化简得:sinBcosC+sinCcosB=2sinB,
即sin(B+C)=2sinB,
∵sin(B+C)=sinA,
∴sinA=2sinB,
利用正弦定理化简得:a=2b,则=2.
故答案为:2
10. 答案:
解析: 由三角形面积公式得
×3×4·sin C=,sin C=.
又∵△ABC为锐角三角形
∴C=60°.
根据余弦定理
AB2=16+9-2×4×3×=13.
AB=.
11. 答案: 45°
解析: a2=b2+c2-2bccos A,又已知a2+4S=b2+c2,故S=bccos A=bcsin A,从而sin A=cos A,tan A=1,A=45°.
12. 解析:b2=a2+c2-2accosB=(3/)2+22-2·3/·2·(-/)=49.
∴ b=7,
S△=/acsinB=/×3/×2×/=//.
13. 解析:
(1)由余弦定理知,
,所以.
(2)由正弦定理知,,所以.
因为AB<BC,所以C为锐角,则.
因此.
14.解析:
∵且,∴,,
∵, ∴,即,
又∵, ∴ ,
即 ,
∴,
∵ , ∴,即,
故.
15. 解析:(1)由正弦定理可得
故 =
所以,
又 ,故 ,所以
或B= ,
因此(舍去) 或
所以
(II)由得,故有
,
因,得.
又,,所以.
当时,;
当时,.
综上,或.
【学习目标】
1.进一步巩固正弦定理和余弦定理,并能综合运用两个定理解决三角形的有关问题;
2.学会用方程思想解决有关三角形的问题,提高综合运用知识的能力和解题的优化意识.
【要点梳理】
要点一、正弦定理和余弦定理的概念
①正弦定理公式:
(其中R表示三角形的外接圆半径)
②余弦定理公式:
第一形式:
第二形式:
要点二、三角形的面积公式
① ;
②;
要点三、利用正、余弦定理解三角形
已知两边和一边的对角或已知两角及一边时,通常选择正弦定理来解三角形;已知两边及夹角或已知三边时,通常选择余弦定理来解三角形.特别是求角时尽量用余弦定理来求,尽量避免分类讨论.
在中,已知和A时,解的情况主要有以下几类:
①若A为锐角时:
/ /
一解 一解
/ /
两解 无解
②若A为直角或钝角时:
要点四、三角形的形状的判定
特殊三角形的判定:
(1)直角三角形
勾股定理:,
互余关系:,,;
(2)等腰三角形
,;
用余弦定理判定三角形的形状(最大角的余弦值的符号)
(1)在中,;
(2)在中,;
(3)在中,;
要点五、解三角形时的常用结论
在中,,
(1)在中
(2)互补关系:,
,
;
(3)互余关系:,
,
.
【典型例题】
类型一:利用正、余弦定理解三角形
例1. 在中,已知下列条件,解三角形.
(1), , ;
(2),,.
【思路点拨】
(1)题中利用正弦定理先求,再求和;
(2)题中利用余弦定理求;求可以利用余弦定理,也可以利用正弦定理。
【解析】
(1)∵,
法一:∵,∴,即,
∴,,.
法二:∵, ∴或,
①当时,,;
②当时,(舍去).
(2)∵
∴
法一:∵
∴,
法二:∵
又∵,即
∴,有,
∴,.
【总结升华】
①解三角形时,可以依据题意画出恰当的示意图,然后正确选择正、余弦定理解答;
②解三角形时,要留意三角形内角和为180°、同一个三角形中大边对大角等性质的应用。
举一反三:
【变式1】 △ABC中,已知c=1,b=,∠B=45°,求∠C和a.
【答案】∵,(舍)
或由正弦定理得:.
【变式2】在中, 求角;
【答案】.
【变式3】在中,若,,,求角和.
【答案】根据余弦定理:,
∵,
∴,。
例2、(2018 浙江)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知/.
(1)求tanC的值;
(2)若△ABC的面积为3,求b的值。
【答案】(1)2;(2)3.
【思路分析】(1)根据正弦定理可将条件中的边之间的关系转化为角之间满足的关系,再将式子作三角恒等变形即可求解;(2)根据条件首先求得sinB的值,再结合正弦定理以及三角形面积的计算公式即可求解.
【解析】(1)由及正弦定理得,∴-cos2B=sin2C,
又由,即,得-cos2B=sin2C=2sinCcosC,解得tanC=2;
(2)由tanC=2,C∈(0,π)得,
又,由正弦定理得,
又,故b=3.
【总结升华】
对于求解三角形的题目,一般都可有两种思路:边化角或角化成边,但要根据结论的形式选择转成边或者角。
举一反三:
【变式】△ABC中,A=45°,a=2,求b和B,C.
【答案】
解法一 :正弦定理
由
若C=60°,则B=75°,
若C=120°,则B=15°,
解法二:余弦定理
若
若
解法三:正余弦定理
若
∵b>c>a,所以B>C>A,所以B=75°,C=60°;
若
∵c>a>b,所以C>A>B,所以B=15°,C=120°.
类型二:正、余弦定理的综合应用
例3.已知△ABC 中,试判断△ABC的形状.
【思路点拨】
题目中给的是角与边的混合关系式,可用正弦定理化简成单一的角的关系;也可以用正弦定理、余弦定理化简成单一的边的关系,然后判断.
【解析】
方法一:用余弦定理化角为边的关系
由得,
整理得,
即,
当时,为等腰三角形;
当即时,则为直角三角形;
综上:为等腰或直角三角形。
方法二:用正弦定理化边为角的关系
由正弦定理得:
即,
∵,
∴
即
∵
∴或,即或
故为等腰三角形或直角三角形。
【总结升华】
(1)要判断三角形的形状特征,必须深入研究边与边的大小关系:是否两边相等?是否三边相等?是否符合勾股定理?还要研究角与角的大小关系:是否两个角相等?是否三个角相等?有无直角或钝角?
(2)解题的思想方法是:从条件出发,利用正、余弦定理等进行代换、转化、化简、运算,找出边与边的关系或角与角的关系,从而作出正确判断。
(3)一般有两种转化方向:要么转化为边,要么转化为角。
(4)判断三角形形状时,用边做、用角做均可。一般地,题目中给的是角,就用角做;题目中给的是边,就用边做,边角之间的转换可用正弦定理或余弦定理。
(5),不要丢解。
举一反三:
【变式1】根据下列条件,试判断△ABC的形状.
(1)bcosA=acosB;(2)a=2bcosC
【答案】
(1)解法一:正弦定理
由bcosA=acosB得2RsinBcosA=2RsinAcosB,
即sin(B-A)=0,于是B=A,
∴△ABC为等腰三角形.
解法二:余弦定理
由bcosA=acosB得,即a2=b2,
所以a=b,△ABC为等腰三角形.
(2)解法一:正弦定理
由a=2bcosC得2RsinA=4RsinBcosC,有sin(B+C)=2sinBcosC,得出sin(B-C)=0,
即B=C,△ABC为等腰三角形;
解法二:余弦定理
由a=2bcosC得,得b2=c2,
即b=c,△ABC等腰三角形.
【变式2】在△ABC中,根据下列条件决定三角形形状.
(1);(2).
【答案】
(1)由
,
则该三角形为直角三角形;
(2)∵,
∴,
由正弦定理得:,
∵中,, ,
∴,即,
∴或,即:或,
∴是等腰三角形或直角三角形.
例4. (2017 四川理)在△ABC中,角A,B,C所对的边分别是a,b,c,且.
(I)证明:;
(II)若,求.
【答案】(I)略(II)4
【思路点拨】第一问,利用正弦定理,将边角进行转化,结合诱导公式进行证明;第二问,利用余弦定理解出,在根据平方关系解出,代入已知中,解出的值。
【解析】(I)根据正弦定理,可设
则
代入中,有
,变形可得
在中,由 ,有
所以
(II)由已知,,根据余弦定理,有
由(),
所以
故
举一反三:
【变式】(2017 天津文)在中,内角所对应的边分别为a,b,c,已知.
(Ⅰ)求B;
(Ⅱ)若,求sinC的值.
【答案】(Ⅰ)在中,由,可得,又由得
,
所以 得
(Ⅱ)由得 则,
所以
例5.锐角 中,a,b,c分别是角A,B,C的对边。
若求的大小
取最大值时,求的大小
【思路点拨】在(1)中,将所给边的关系式化简变形后,根据结构形式可判断出应该用余弦定理。
【解析】(1)∵, ∴,
故由余弦定理得
∵A是锐角三角形的内角,所以
∴
(2)=
当且仅当时取等号
∴
【总结升华】
对于三角形中边角的最大值或最小值问题可以运用正弦定理或余弦定理建立所求变量与三角形的角或边之间的函数关系,利用正、余弦函数的有界性或二次函数的知识解决问题
举一反三:
【变式1】已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)(sinA-sinB)=(c-b)sinC,则△ABC面积的最大值为 .
答案:
解析:∵△ABC中, a=2,且(2+b)(sinA-sinB)=(c-b)sinC,
∴利用正弦定理可得 4-b2=(c-b)c,即 b2+c2-bc=4.
再利用基本不等式可得 4≥2bc-bc=bc,∴bc≤4,当且仅当b=c=2时,取等号,
此时,△ABC为等边三角形,它的面积为bc·sinA=,
故答案为:.
【变式2】在中,三内角满足的方程
有两个相等的根。
求证:角B不大于
(2)当角B取最大值时,判断的形状
【答案】
(1)由韦达定理得即,
由正弦定理,有2b=a+c
由余弦定理得
∴
(2)当角B取最大值时,,且a=c,易知为正三角形
【巩固练习】
一、选择题
1.(2017 新课标Ⅲ理)在/中,/,BC边上的高等于/,则/( )
A./ B./ C./ D./
2.中,若,则有( )
A. B. C. D.、大小不能确定
3.在△ABC中,若a=7,b=3,c=8,则△ABC的面积等于( )
A.12 B.
C.28 D.
4.边长为的三角形的最大角与最小角的和是( )
A. B. C. D.
5.钝角三角形ABC的面积是,AB=1,BC=,则AC=( )
A. 5 B. C. 2 D. 1
二、填空题
6. 在中,已知,则的度数为 .
7. (2017 新课标Ⅱ理) /的内角/的对边分别为/,若/,/,/,则/ .
8.在△ABC中,A=60°,AC=4,BC=,则△ABC的面积等于 .
9. 在△ABC中,角A,B,C所对应的边分别为a,b,c,已知bcosC+ccosB=2b,则= .
10. 锐角△ABC的面积为,BC=4,CA=3,则AB=________.
11.在△ABC中,三边a,b,c与面积S的关系式为a2+4S=b2+c2,则角A为________.
三、解答题
12.已知a=3/,c=2,B=150°,求边b的长及S△.
13.(2018 江苏)在△ABC中,已知AB=2,AC=3,A=60°.
(1)求BC的长;
(2)求sin2C的值.
14. 已知的三角内角、、有2B=A+C,三边、、满足.
求证:.
15. (2017 浙江理)在△ABC中,内角A,B,C所对的边分别为a,b,c. 已知b+c=2a cos B.
(I)证明:A=2B;
(II)若△ABC的面积,求角A的大小.
【答案与解析】
1. 答案: C
解析:设/边上的高线为/,则/,所以/,/.由余弦定理,知/,故选C.
2. 答案: C
解析:∵,∴由正弦定理有,
即,整理得
即, ∴
3答案: D
.解析: 由余弦定理可得cos A=,A=60°,∴S△ABC=bcsin A
=.故选D.
4. 答案:B
解析: 设中间角为,则为所求
5. 答案:B
解析:∵钝角三角形ABC的面积是,AB=c=1,BC=a=,
∴S=acsinB=,即sinB=,
当B为钝角时,cosB=-=-,
利用余弦定理得:AC2=AB2+BC2-2AB?BC?cosB=1+2+2=5,即AC=,
当B为锐角时,cosB==,
利用余弦定理得:AC2=AB2+BC2-2AB?BC?cosB=1+2-2=1,即AC=1,
此时AB2+AC2=BC2,即△ABC为直角三角形,不合题意,舍去,
则AC=.
故选:B.
6.解析:∵,∴,
∴,∴
7.解析:∵ ,且为三角形内角,所以
= ,又因为 所以
.
8. 答案:.
解析:∵△ABC中,A=60°,AC=4,BC=,
由正弦定理得:,
∴,解得sinB=1,
∴B=90°,C=30°,
∴△ABC的面积=
故答案为:.
9. 答案:2
解析:将bcosC+ccosB=2b,利用正弦定理化简得:sinBcosC+sinCcosB=2sinB,
即sin(B+C)=2sinB,
∵sin(B+C)=sinA,
∴sinA=2sinB,
利用正弦定理化简得:a=2b,则=2.
故答案为:2
10. 答案:
解析: 由三角形面积公式得
×3×4·sin C=,sin C=.
又∵△ABC为锐角三角形
∴C=60°.
根据余弦定理
AB2=16+9-2×4×3×=13.
AB=.
11. 答案: 45°
解析: a2=b2+c2-2bccos A,又已知a2+4S=b2+c2,故S=bccos A=bcsin A,从而sin A=cos A,tan A=1,A=45°.
12. 解析:b2=a2+c2-2accosB=(3/)2+22-2·3/·2·(-/)=49.
∴ b=7,
S△=/acsinB=/×3/×2×/=//.
13. 解析:
(1)由余弦定理知,
,所以.
(2)由正弦定理知,,所以.
因为AB<BC,所以C为锐角,则.
因此.
14.解析:
∵且,∴,,
∵, ∴,即,
又∵, ∴ ,
即 ,
∴,
∵ , ∴,即,
故.
15. 解析:(1)由正弦定理可得
故 =
所以,
又 ,故 ,所以
或B= ,
因此(舍去) 或
所以
(II)由得,故有
,
因,得.
又,,所以.
当时,;
当时,.
综上,或.
