人教版高中数学必修5同步练习题、期中、期末复习资料、补习资料:08【提高】解三角形应用举例
文档属性
| 名称 | 人教版高中数学必修5同步练习题、期中、期末复习资料、补习资料:08【提高】解三角形应用举例 |

|
|
| 格式 | zip | ||
| 文件大小 | 555.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-30 11:10:16 | ||
图片预览



文档简介
解三角形应用举例
【学习目标】
1.能够利用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的问题;
2.提高运用所学知识解决实际问题的能力,并初步掌握数学建模的思想方法;
3.掌握运用正弦定理、余弦定理解决几何计算问题的方法.
【学习策略】
解斜三角形的知识主要用于测量及航海两大类型问题.实际应用中,首先要弄清题意,画出直观示意图,将实际问题转化为解三角形的问题,再确定是哪类解三角形问题,即应用哪个定理来解决.
【要点梳理】
要点一、解三角形应用题的步骤
解三角形在实际中应用非常广泛,如测量、航海、几何、物理等方面都要用到解三角形的知识,解题时应认真分析题意,并做到算法简练,算式工整,计算正确.其解题的一般步骤是:
(1)准确理解题意,尤其要理解应用题中的有关名词和术语;明确已知和所求,理清量与量之间的关系;
(2)根据题意画出示意图,并将已知条件在图形中标出,将实际问题抽象成解三角形模型;
(3) 分析与所研究的问题有关的一个或几个三角形,正确运用正弦定理和余弦定理,有顺序的求解;
(4)将三角形的解还原为实际问题,注意实际问题中的单位及近似计算要求,回答实际问题.
要点二、解三角形应用题的基本思路
实际问题 画图 数学问题 解三角形 数学问题的解 检验 实际问题的解
要点三、实际问题中的一些名词、术语
仰角和俯角
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫仰角,目标视线在水平视线下方时叫俯角,如图所示:
/
坡角和坡度
坡面与地平面所成的角度,叫做坡角;坡面的铅直高度和水平宽度的比叫做坡度或者坡比,常用字母i表示。坡比是坡角的正切值。
方位角与方向角:
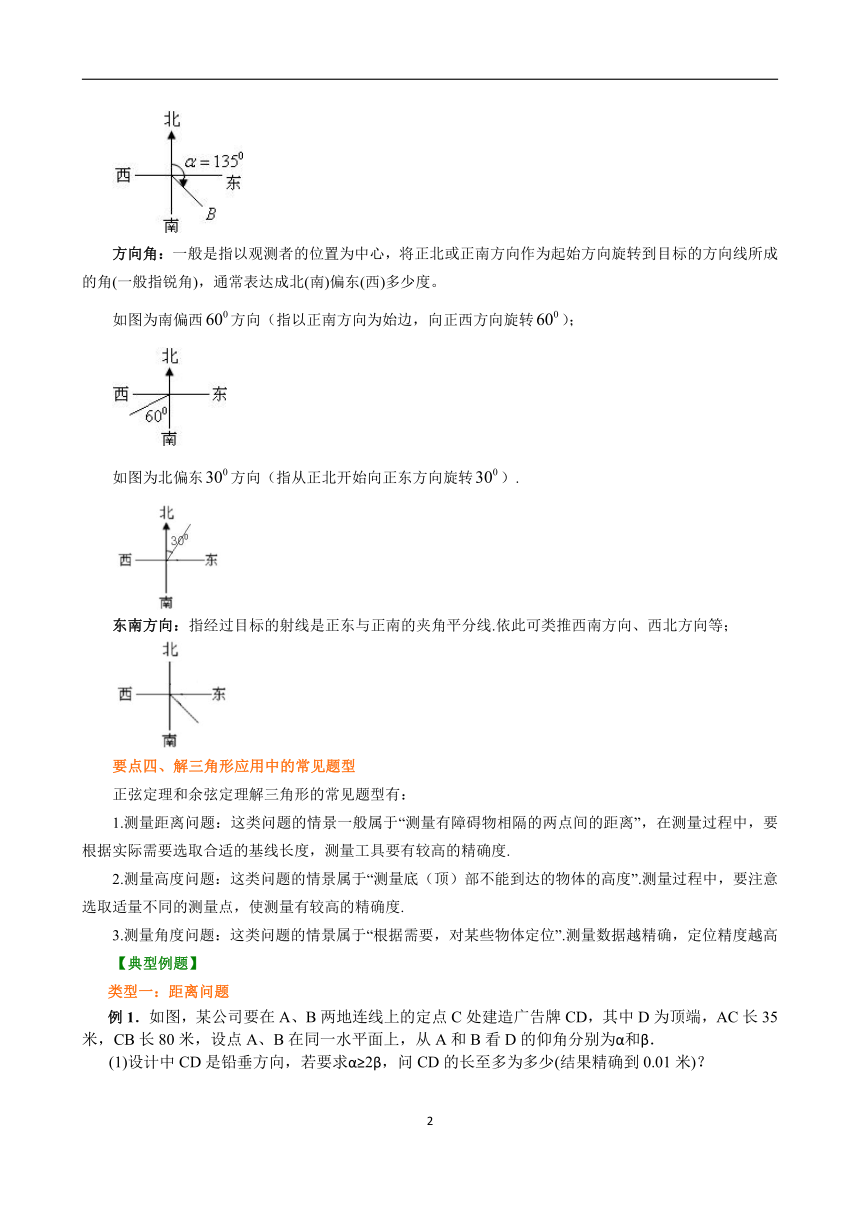
方位角:一般指正北方向线顺时针到目标方向线的水平角。方位角的取值范围为0°~360°。
如图,点的方位角是。
/
方向角:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)多少度。
如图为南偏西方向(指以正南方向为始边,向正西方向旋转);
/
如图为北偏东方向(指从正北开始向正东方向旋转).
/
东南方向:指经过目标的射线是正东与正南的夹角平分线.依此可类推西南方向、西北方向等;
/
要点四、解三角形应用中的常见题型
正弦定理和余弦定理解三角形的常见题型有:
1.测量距离问题:这类问题的情景一般属于“测量有障碍物相隔的两点间的距离”,在测量过程中,要根据实际需要选取合适的基线长度,测量工具要有较高的精确度.
2.测量高度问题:这类问题的情景属于“测量底(顶)部不能到达的物体的高度”.测量过程中,要注意选取适量不同的测量点,使测量有较高的精确度.
3.测量角度问题:这类问题的情景属于“根据需要,对某些物体定位”.测量数据越精确,定位精度越高
【典型例题】
类型一:距离问题
例1.如图,某公司要在A、B两地连线上的定点C处建造广告牌CD,其中D为顶端,AC长35米,CB长80米,设点A、B在同一水平面上,从A和B看D的仰角分别为α和β.
(1)设计中CD是铅垂方向,若要求α≥2β,问CD的长至多为多少(结果精确到0.01米)?
(2)施工完成后,CD与铅垂方向有偏差,现在实测得α=38.12°,β=18.45°,求CD的长(结果精确到0.01米).
/
【答案】(1) 28.28米.(2) 26.93米.
【思路点拨】
(1)这是一道关于求两点之间的距离问题。题目条件告诉了边AC、CB的长以及以A、C为顶点的两个角,根据正切函数的定义及性质得到一个关于x的不等式,解之得到CD的长度。(2)根据三角形的内角和定理和正弦定理,解得CD的长。
【解析】(1)设CD的长为x米,则tanα=,tanβ=,
∵,
∴tanα≥tan2β,
∴,
即,
解得0,
即CD的长至多为28.28米.
(2)设DB=a,DA=b,CD=m,
则∠ADB=180°-α-β=123.43°,
由正弦定理得,
即,
∴,
答:CD的长为26.93米.
【总结升华】
1. 此题虽为解三角形问题的简单应用,但关键是把未知边所处的三角形找到,在转换过程中应注意排除题目中非数学因素的干扰,将数量关系从题目准确地提炼出来.
2. 解三角形的应用题时,通常会遇到两种情况:
(1)已知量与未知量全部集中在一个三角形中,依次利用正弦定理或余弦定理解之。
(2)已知量与未知量涉及两个或几个三角形,这时需要选择条件足够的三角形优先研究,再逐步在其余的三角形中求出问题的解。
3. 在研究三角形时,灵活根据两个定理可以寻找到多种解决问题的方案,但有些过程较繁复,如何找到最优的方法,最主要的还是分析两个定理的特点,结合题目条件来选择最佳的计算方式。
举一反三:
【变式1】如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN= m.
/
【答案】△ABC中,∵∠BAC=45°,∠ABC=90°,BC=100,
∴AC==100.
△AMC中,∵∠MAC=75°,∠MCA=60°,
∴∠AMC=45°,由正弦定理可得,
即 ,解得AM=100.
Rt△AMN中,MN=AM?sin∠MAN=100×sin60°=150(m),
故答案为:150.
【变式2】为了开凿隧道,要测量隧道上D、E间的距离,为此在山的一侧选取适当点C,如图,测得CA=400m,CB=600m, ∠ACB=60°,又测得A、B两点到隧道口的距离AD=80m,BE=40m(A、D、E、B在一条直线上),计算隧道DE的长.
【答案】在△ABC中,CA=400m,CB=600m, ∠ACB=60°,
由余弦定理得
∴
∴
答:隧道长约为409.2m.
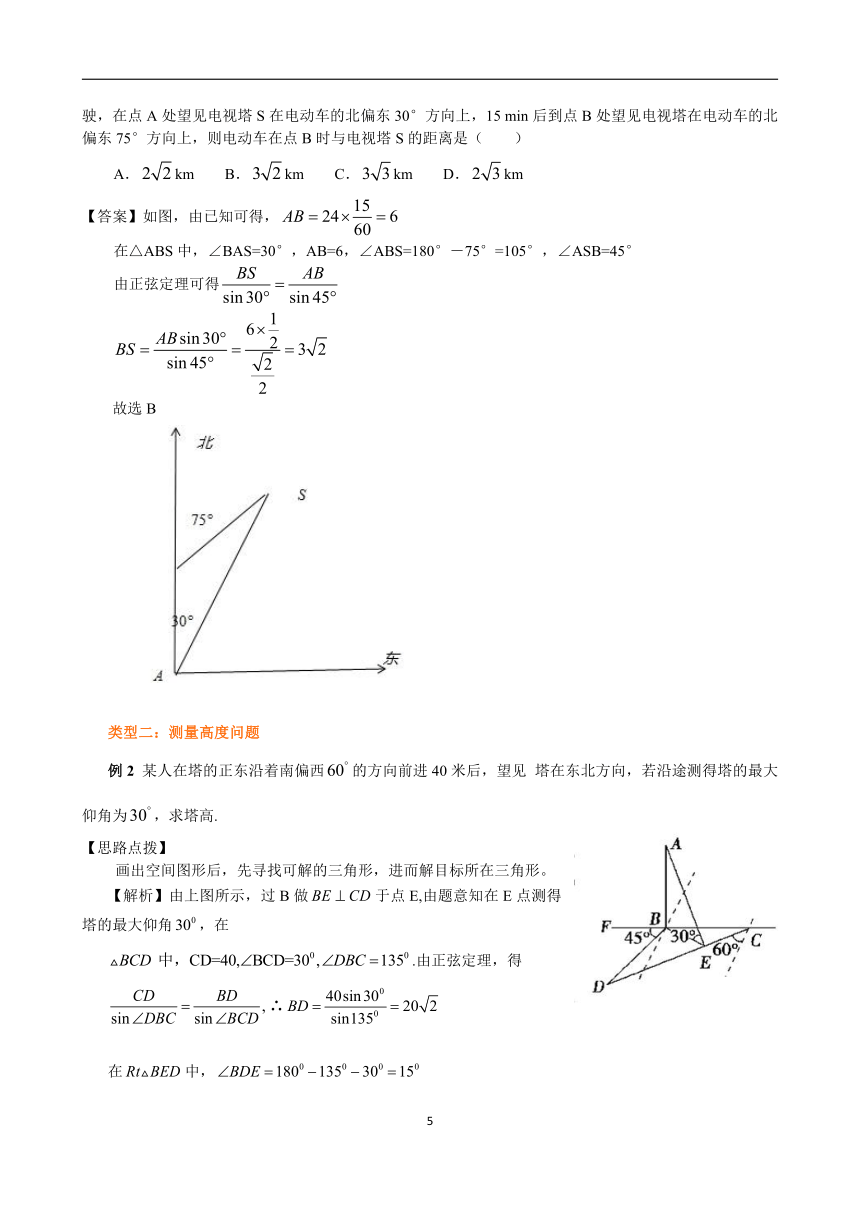
【变式3】(2017春 邢台校级期中)张晓华同学骑电动自行车以24 km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15 min后到点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是( )
A.km B.km C.km D.km
【答案】如图,由已知可得,
在△ABS中,∠BAS=30°,AB=6,∠ABS=180°-75°=105°,∠ASB=45°
由正弦定理可得
故选B
/
类型二:测量高度问题
例2 某人在塔的正东沿着南偏西的方向前进40米后,望见 塔在东北方向,若沿途测得塔的最大仰角为,求塔高.
【思路点拨】
画出空间图形后,先寻找可解的三角形,进而解目标所在三角形。
【解析】由上图所示,过B做于点E,由题意知在E点测得塔的最大仰角,在
.由正弦定理,得
∴
在中,
∴
在中,∴(米)
故所求塔高为米
【总结升华】 测量高度是在与地面垂直的竖直平面内构造三角形,在依条件结合正弦定理和余弦定理来解,解决测量高度的问题时,常出现仰角与俯角的问题,要注意它们的区别与联系.
举一反三:
【变式1】(2017 绵阳校级模拟)如图,无人机在离地面高200 m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为________m。
/
【答案】在Rt△ABC中,∠ACB=∠DAC=45°,∠ABC=90°,AB=200,
∴,
∵∠MCN=60°,∴∠ACM=180°-∠MCN-∠ACN=75°,
∵∠MAC=15°+45°=60°,∴∠AMC=180°-∠MAC-∠ACM=45°。
在△MAC中,由正弦定理得,即
解得。
∵,
∴。
故答案为:300。
【变式2】在某点B处测得建筑物AE的顶端A的仰角为,沿BE方向前进30m,至点C处测得顶端A的仰角为2,再继续前进10m至D点,测得顶端A的仰角为4,求的大小和建筑物AE的高。
【答案】所求角,建筑物高度为15m。
类型三:方位角问题
例3 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路南侧远处一山顶D在西偏北的方向上,行驶后到达B处,测得此山顶在西偏北的方向上,仰角为,求此山的高度CD.
/
【思路点拨】
欲求出CD,只需在BCD中求出BD或BC,而在BCD中先求BC边比较适合;或设CD=x,列方程解答.
【解析】方法一:在ABC中, ,,,
根据正弦定理: = ,有,
∴ .
方法二:设CD=x,则,
根据正弦定理: = ,有,
∴,解得,即.
【总结升华】正确地画出其空间示意图是解题的关键.
举一反三:
【变式1】两灯塔A、B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏西30,灯塔B在观察站C南偏西60,则A、B之间的距离为 ;
【答案】;
/
如图,,,。
【变式2】如图示,已知两座灯塔A和B与海洋观察站C的距离都等于,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( ? )
/
A. ? B. C.? D.
【答案】B
类型四:航海问题
例4如图所示,在海岸A处,发现北偏东45°方向,距A为()km的B处有一艘走私船.在A处北偏西75°方向,距A为2 km的C处的缉私船奉命以km/h的速度追截走私船.此时走私船正以10km/h的速度从B处向北偏东30°方向逃窜,则缉私船沿什么方向能最快追上走私船?并求出所需要的时间.
/
【思路点拨】这里必须弄清楚三个概念:
(1)方位角;
(2)沿什么方向追,即按什么方位角航行;
(3)最快追上,即应理解为按直线航行,且两船所用时间相等,画出示意图,即可求出CD的方位角及由C到D所需航行的时间.
【解析】设缉私船追上走私船需,则,.
由余弦定理,得
,
由正弦定理,得,
∴,而,
∴
∴,.
∴,即,∴
答:缉私船向东偏北方向,只需便能追上走私船.
【总结升华】航海问题中关键是方向角的表示,最好要参照方向坐标,准确的画出图形.
举一反三:
【变式1】如图A,B是海面上位于东西方向相距5(3+)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救,其航行速度为30海里/小时,求该救援船到达D点需要多长时间?
【答案】 由题意知AB=5(3+)海里,∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30°)=105°,
在△DAB中,由正弦定理得
∴DB
=
=
=10 (海里)
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°
BC=20海里
在△DBC中,由余弦定理得
CD2=BD2+BC2-2BD·BC·cos∠DBC
=300+1 200-2×10×20×=900
∴CD=30(海里),则需要的时间t==1(小时)
答:救援船到达D点需要1小时.
【变式2】如图所示,海中小岛A的周围38海里内有暗礁,某船正由北向南航行,在B处测得小岛A在船的南偏东,航行30海里后,在C处测得小岛A在船的南偏东,如果此船不改变航向,继续向南航行,有无触礁危险?
【答案】船继续向南航行,有无触礁的危险,取决于A到直线BC的距离与38海里的大小.于是,只要先算出AC(或AB),再算出A到BC所在直线的距离,将它与38海里比较即得问题的解.
在中,,,,
∴,
由正弦定理知:,∴
∴
于是A到BC所在直线的距离为(海里)
它大于38海里,所以继续向南航行无触礁危险.
【巩固练习】
选择题
1.如图,设A,B两点在河的两岸,一测量者在A的同侧,在A所在的河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
A. m B. m
C. m D. m
2.(2017春 孝感期中)如图,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=100米,点C位于BD上,则山高AB等于( )
A.100米 B.米 C.米 D.米
3.如图,从气球A上测得正前方的河流的两岸B、C的俯角分别为75°、30°,此时气球的高是60m,则河流的宽度BC等于( )
/
A.240(-1)m B. 180(-1)m C. 120(-1)m D. 30(+1)m
4.如右图,为了测量隧道口AB的长度,给定下列四组数据,测量时应当用数据( )
A.α,a,b B.α,β,a
C.a,b,γ D.α,β,b
5.有一长为10m的斜坡,倾斜角为,在不改变坡高和坡顶的前提下,要通过加长坡面的方法将它的倾斜角改为,则坡底要延长( )
A.5m B.10m C.m D.m
6.(2017 遂宁模拟改编)海轮“和谐号”从A处以每小时21海里的速度出发,海轮“奋斗号”在A处北偏东45°的方向,且与A相距10海里的C处,沿北偏东105°的方向以每小时9海里的速度行驶,则海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为( )小时。
A. B. C. D.1
填空题
7. 一艘船以的速度向正北方向航行,船在处看见灯塔在船的东北方向上,后船在处看见灯塔在船的北偏东的方向上,这时,船与灯塔的距离 ;
8. (2018 湖北高考)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=_________m.
/
9. 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于 m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,≈1.73)
/
解答题
10.如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时,两船之间的距离最短?
/
11.为保障高考的公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1千米处不能收到手机信号,检查员抽查某市一考点,在考点正西约1.732千米有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以每小时12千米的速度沿公路行驶,问最长需要多少分钟,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
12.一辑私艇发现在北偏东45°方向,距离12海里的海里上有一走私船正以10海里/小时的速度沿南偏东75°方向逃窜,若辑私艇的速度为14海里,辑私艇沿北偏东 的方向追去,若要在最短的时间内追上该走私船,求追及所需的时间和角的正弦值.
13. 如图,A、B是水平面上的两个点,相距800m,在A点测得山顶C的仰角为25°,∠BAD=110°,又在B点测得∠ABD=40°,其中D是点C在水平面上的垂足,求山高CD.(精确到1m)
14.如图,一艘海轮从A出发,沿北偏东的方向航行后到达海岛B,然后从B出发,沿北偏东的方向航行后达到海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?
/
15. 如图所示,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上的一个动点,以PC为边作等边△PCD,且点D与圆心O分别在PC的两侧,求四边形OPDC面积的最大值.
16. (2017 南通模拟)如图,景点A在景点B的正北方向2千米处,景点C在景点D的正东方向千米处。
(1)游客甲沿CA从景点C出发行至景点B相距千米的点P处,记∠PBC=α,求sinα的值;
(2)甲沿CA从景点C出发前往景点A,乙沿AB从景点A出发前往景B,甲乙同时出发,甲的速度为1千米/小时,乙的速度为2千米/小时。若甲乙两人这间通过对讲机联系,对讲机在该景区内的最大通话距离为3千米,问有多长时间两人不能通话?(精确到0.1小时,参考数据:)
/
【答案与解析】
1.答案: A
解析:在△ABC中,AC=50,∠ACB=45°,∠CAB=105°
∴∠ABC=30°,由正弦定理:
∴AB==m.故选A.
2. 答案: D
解析:设AB=x m,则由题意,∠D=30°,∠ACB=45°,
在Rt△ABC中,BC=AB=x,
在Rt△ADB中,DB=CD+BC=100+x,
∴,即,解得。
∴山AB的高度为米。
故选D。
3. 答案:C
解析:如图,
/
由图可知,∠DAB=15°,
∵
在Rt△ADB中,又AD=60,
∴DB=AD?tan15°=60×(2-)=120-60.
在Rt△ADB中,∠DAC=60°,AD=60,
∴DC=AD?tan60°=60.
∴BC=DC-DB=60-(120-60)=120()(m).
∴河流的宽度BC等于120()m.
故选:C.
4. 答案: C
解析: 由A与B不可到达,故不易测量α,β,故选C.
5. 答案: C
解析:在△ABB’中由正弦定理,得
6. 答案: B
解析:设海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为x小时,
/
如图,则由已知得△ABC中,AC=10,AB=21x,BC=9x,∠ACB=120°,
由余弦定理得:(21x)2=100+(9x)2-2×10×9x×cos120°,
整理,得36x2―9x―10=0,
解得或(舍)。
∴海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为小时。
故选:B.
7. 答案:;
如图所示:
/
,,,
在中,根据正弦定理。
8. 答案:/.
解析:
在△ABC中,∠CAB=30°,∠ACB=75°-30°=45°,
根据正弦定理知,,
即,
所以,故应填.
9. 答案:;
解析
过A点作AD垂直于CB的延长线,垂足为D,
则Rt△ACD中,∠C=30°,AD=46m
∴.
又∵Rt△ABD中,∠ABD=67°,可得
∴BC=CD-BD=79.58-19.5=60.08≈60m
故答案为:60m
/
10.解析:设航行x小时后甲船到达C点,乙船到达D点,在△BCD中,BC=(100-50x)海里,BD=30x海里(), ∠CBD=60°,由余弦定理得:
∴当(小时)时,CD2最小,从而得CD最小
∴航行小时,两船之间距离最近.
11.解析: 如图所示,考点为A,检查开始处为B,设公路上C、D两点到考点的距离为1千米.
/
在△ABC中,AB=≈1.732,AC=1,∠ABC=30°,
由正弦定理sin∠ACB=·AB=,
∴∠ACB=120°(∠ACB=60°不合题意),
∴∠BAC=30°,∴BC=AC=1,
在△ACD中,AC=AD,∠ACD=60°,
∴△ACD为等边三角形,∴CD=1.
∵×60=5,∴在BC上需5分钟,CD上需5分钟.
答:最长需要5分钟检查员开始收不到信号,并持续至少5分钟才算合格.
12. 解析:如图所示,A、C分别表示辑私艇,走私船的位置,设经x小时后在B处追上.
则AB=14x,BC=10x,∠ACB=120°
由得x=2.
故AB=28,BC=20
即所需时间2小时,为.
13.
解析:在△ABD中,∠ADB=180°-110°-40°=30°,
由正弦定理得.
在Rt△ACD中,CD=ADtan25°≈480(m).
答:山高约为480m.
14、解析:在中, ,
根据余弦定理,
根据正弦定理, ,
有,
∵ ∴
所以 ,
答:此船应该沿北偏东的方向航行,需要航行
15. 解析:设∠POB=,四边形面积为y,则在△POC中,由余弦定理得:?
PC2=OP2+OC2-2OP·OCcos=5-4cos?
∴y=S△OPC+S△PCD=+(5-4cos)
=2sin(-)+
∴当-=即=时,ymax=2+.
16. 解析:(1)在Rt△ABC中,AB=2,,∴∠C=30°
在△PBC中,由余弦定理得BC2+PC2-2BC·PC·cos30°=BP2,即
化简,得PC2-6PC+5=0,解得PC=1或PC=5(舍去)
在△PBC中,由正弦定理得,即
∴。
(2)Rt△ABC中,BA=2,,
设甲出发后的时间为t小时,则由题意可知0≤t≤4,设甲在线段CA上的位置为点M,AM=4-t
在△PBC中,由余弦定理得BC2+PC2-2BC·PC·cos30°=BP2,
即,化简得PC2-6PC+5=0
解得PC=1或PC=5(舍去)
①当1≤t≤4时,乙在景点B处,甲在线段PA上,甲乙间的距离d≤BP<3,此时不合题意;
②当0≤t<1时,设乙在线段AB上的位置为点Q,则AQ=2t
在△AMQ中,由余弦定理得,MQ2=(4―t)2+(2t)2―2×2t(4-t)×cos60°=7t2-16t+16
令MQ>3即MQ2>9,得7t2-16t+7>0,解得或
∴
综上,当时,甲、乙间的距离大于3米。
又,故两人不能通话的时间大约为0.6小时
【学习目标】
1.能够利用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的问题;
2.提高运用所学知识解决实际问题的能力,并初步掌握数学建模的思想方法;
3.掌握运用正弦定理、余弦定理解决几何计算问题的方法.
【学习策略】
解斜三角形的知识主要用于测量及航海两大类型问题.实际应用中,首先要弄清题意,画出直观示意图,将实际问题转化为解三角形的问题,再确定是哪类解三角形问题,即应用哪个定理来解决.
【要点梳理】
要点一、解三角形应用题的步骤
解三角形在实际中应用非常广泛,如测量、航海、几何、物理等方面都要用到解三角形的知识,解题时应认真分析题意,并做到算法简练,算式工整,计算正确.其解题的一般步骤是:
(1)准确理解题意,尤其要理解应用题中的有关名词和术语;明确已知和所求,理清量与量之间的关系;
(2)根据题意画出示意图,并将已知条件在图形中标出,将实际问题抽象成解三角形模型;
(3) 分析与所研究的问题有关的一个或几个三角形,正确运用正弦定理和余弦定理,有顺序的求解;
(4)将三角形的解还原为实际问题,注意实际问题中的单位及近似计算要求,回答实际问题.
要点二、解三角形应用题的基本思路
实际问题 画图 数学问题 解三角形 数学问题的解 检验 实际问题的解
要点三、实际问题中的一些名词、术语
仰角和俯角
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫仰角,目标视线在水平视线下方时叫俯角,如图所示:
/
坡角和坡度
坡面与地平面所成的角度,叫做坡角;坡面的铅直高度和水平宽度的比叫做坡度或者坡比,常用字母i表示。坡比是坡角的正切值。
方位角与方向角:
方位角:一般指正北方向线顺时针到目标方向线的水平角。方位角的取值范围为0°~360°。
如图,点的方位角是。
/
方向角:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)多少度。
如图为南偏西方向(指以正南方向为始边,向正西方向旋转);
/
如图为北偏东方向(指从正北开始向正东方向旋转).
/
东南方向:指经过目标的射线是正东与正南的夹角平分线.依此可类推西南方向、西北方向等;
/
要点四、解三角形应用中的常见题型
正弦定理和余弦定理解三角形的常见题型有:
1.测量距离问题:这类问题的情景一般属于“测量有障碍物相隔的两点间的距离”,在测量过程中,要根据实际需要选取合适的基线长度,测量工具要有较高的精确度.
2.测量高度问题:这类问题的情景属于“测量底(顶)部不能到达的物体的高度”.测量过程中,要注意选取适量不同的测量点,使测量有较高的精确度.
3.测量角度问题:这类问题的情景属于“根据需要,对某些物体定位”.测量数据越精确,定位精度越高
【典型例题】
类型一:距离问题
例1.如图,某公司要在A、B两地连线上的定点C处建造广告牌CD,其中D为顶端,AC长35米,CB长80米,设点A、B在同一水平面上,从A和B看D的仰角分别为α和β.
(1)设计中CD是铅垂方向,若要求α≥2β,问CD的长至多为多少(结果精确到0.01米)?
(2)施工完成后,CD与铅垂方向有偏差,现在实测得α=38.12°,β=18.45°,求CD的长(结果精确到0.01米).
/
【答案】(1) 28.28米.(2) 26.93米.
【思路点拨】
(1)这是一道关于求两点之间的距离问题。题目条件告诉了边AC、CB的长以及以A、C为顶点的两个角,根据正切函数的定义及性质得到一个关于x的不等式,解之得到CD的长度。(2)根据三角形的内角和定理和正弦定理,解得CD的长。
【解析】(1)设CD的长为x米,则tanα=,tanβ=,
∵,
∴tanα≥tan2β,
∴,
即,
解得0,
即CD的长至多为28.28米.
(2)设DB=a,DA=b,CD=m,
则∠ADB=180°-α-β=123.43°,
由正弦定理得,
即,
∴,
答:CD的长为26.93米.
【总结升华】
1. 此题虽为解三角形问题的简单应用,但关键是把未知边所处的三角形找到,在转换过程中应注意排除题目中非数学因素的干扰,将数量关系从题目准确地提炼出来.
2. 解三角形的应用题时,通常会遇到两种情况:
(1)已知量与未知量全部集中在一个三角形中,依次利用正弦定理或余弦定理解之。
(2)已知量与未知量涉及两个或几个三角形,这时需要选择条件足够的三角形优先研究,再逐步在其余的三角形中求出问题的解。
3. 在研究三角形时,灵活根据两个定理可以寻找到多种解决问题的方案,但有些过程较繁复,如何找到最优的方法,最主要的还是分析两个定理的特点,结合题目条件来选择最佳的计算方式。
举一反三:
【变式1】如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN= m.
/
【答案】△ABC中,∵∠BAC=45°,∠ABC=90°,BC=100,
∴AC==100.
△AMC中,∵∠MAC=75°,∠MCA=60°,
∴∠AMC=45°,由正弦定理可得,
即 ,解得AM=100.
Rt△AMN中,MN=AM?sin∠MAN=100×sin60°=150(m),
故答案为:150.
【变式2】为了开凿隧道,要测量隧道上D、E间的距离,为此在山的一侧选取适当点C,如图,测得CA=400m,CB=600m, ∠ACB=60°,又测得A、B两点到隧道口的距离AD=80m,BE=40m(A、D、E、B在一条直线上),计算隧道DE的长.
【答案】在△ABC中,CA=400m,CB=600m, ∠ACB=60°,
由余弦定理得
∴
∴
答:隧道长约为409.2m.
【变式3】(2017春 邢台校级期中)张晓华同学骑电动自行车以24 km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15 min后到点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是( )
A.km B.km C.km D.km
【答案】如图,由已知可得,
在△ABS中,∠BAS=30°,AB=6,∠ABS=180°-75°=105°,∠ASB=45°
由正弦定理可得
故选B
/
类型二:测量高度问题
例2 某人在塔的正东沿着南偏西的方向前进40米后,望见 塔在东北方向,若沿途测得塔的最大仰角为,求塔高.
【思路点拨】
画出空间图形后,先寻找可解的三角形,进而解目标所在三角形。
【解析】由上图所示,过B做于点E,由题意知在E点测得塔的最大仰角,在
.由正弦定理,得
∴
在中,
∴
在中,∴(米)
故所求塔高为米
【总结升华】 测量高度是在与地面垂直的竖直平面内构造三角形,在依条件结合正弦定理和余弦定理来解,解决测量高度的问题时,常出现仰角与俯角的问题,要注意它们的区别与联系.
举一反三:
【变式1】(2017 绵阳校级模拟)如图,无人机在离地面高200 m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为________m。
/
【答案】在Rt△ABC中,∠ACB=∠DAC=45°,∠ABC=90°,AB=200,
∴,
∵∠MCN=60°,∴∠ACM=180°-∠MCN-∠ACN=75°,
∵∠MAC=15°+45°=60°,∴∠AMC=180°-∠MAC-∠ACM=45°。
在△MAC中,由正弦定理得,即
解得。
∵,
∴。
故答案为:300。
【变式2】在某点B处测得建筑物AE的顶端A的仰角为,沿BE方向前进30m,至点C处测得顶端A的仰角为2,再继续前进10m至D点,测得顶端A的仰角为4,求的大小和建筑物AE的高。
【答案】所求角,建筑物高度为15m。
类型三:方位角问题
例3 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路南侧远处一山顶D在西偏北的方向上,行驶后到达B处,测得此山顶在西偏北的方向上,仰角为,求此山的高度CD.
/
【思路点拨】
欲求出CD,只需在BCD中求出BD或BC,而在BCD中先求BC边比较适合;或设CD=x,列方程解答.
【解析】方法一:在ABC中, ,,,
根据正弦定理: = ,有,
∴ .
方法二:设CD=x,则,
根据正弦定理: = ,有,
∴,解得,即.
【总结升华】正确地画出其空间示意图是解题的关键.
举一反三:
【变式1】两灯塔A、B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏西30,灯塔B在观察站C南偏西60,则A、B之间的距离为 ;
【答案】;
/
如图,,,。
【变式2】如图示,已知两座灯塔A和B与海洋观察站C的距离都等于,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( ? )
/
A. ? B. C.? D.
【答案】B
类型四:航海问题
例4如图所示,在海岸A处,发现北偏东45°方向,距A为()km的B处有一艘走私船.在A处北偏西75°方向,距A为2 km的C处的缉私船奉命以km/h的速度追截走私船.此时走私船正以10km/h的速度从B处向北偏东30°方向逃窜,则缉私船沿什么方向能最快追上走私船?并求出所需要的时间.
/
【思路点拨】这里必须弄清楚三个概念:
(1)方位角;
(2)沿什么方向追,即按什么方位角航行;
(3)最快追上,即应理解为按直线航行,且两船所用时间相等,画出示意图,即可求出CD的方位角及由C到D所需航行的时间.
【解析】设缉私船追上走私船需,则,.
由余弦定理,得
,
由正弦定理,得,
∴,而,
∴
∴,.
∴,即,∴
答:缉私船向东偏北方向,只需便能追上走私船.
【总结升华】航海问题中关键是方向角的表示,最好要参照方向坐标,准确的画出图形.
举一反三:
【变式1】如图A,B是海面上位于东西方向相距5(3+)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救,其航行速度为30海里/小时,求该救援船到达D点需要多长时间?
【答案】 由题意知AB=5(3+)海里,∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30°)=105°,
在△DAB中,由正弦定理得
∴DB
=
=
=10 (海里)
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°
BC=20海里
在△DBC中,由余弦定理得
CD2=BD2+BC2-2BD·BC·cos∠DBC
=300+1 200-2×10×20×=900
∴CD=30(海里),则需要的时间t==1(小时)
答:救援船到达D点需要1小时.
【变式2】如图所示,海中小岛A的周围38海里内有暗礁,某船正由北向南航行,在B处测得小岛A在船的南偏东,航行30海里后,在C处测得小岛A在船的南偏东,如果此船不改变航向,继续向南航行,有无触礁危险?
【答案】船继续向南航行,有无触礁的危险,取决于A到直线BC的距离与38海里的大小.于是,只要先算出AC(或AB),再算出A到BC所在直线的距离,将它与38海里比较即得问题的解.
在中,,,,
∴,
由正弦定理知:,∴
∴
于是A到BC所在直线的距离为(海里)
它大于38海里,所以继续向南航行无触礁危险.
【巩固练习】
选择题
1.如图,设A,B两点在河的两岸,一测量者在A的同侧,在A所在的河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
A. m B. m
C. m D. m
2.(2017春 孝感期中)如图,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=100米,点C位于BD上,则山高AB等于( )
A.100米 B.米 C.米 D.米
3.如图,从气球A上测得正前方的河流的两岸B、C的俯角分别为75°、30°,此时气球的高是60m,则河流的宽度BC等于( )
/
A.240(-1)m B. 180(-1)m C. 120(-1)m D. 30(+1)m
4.如右图,为了测量隧道口AB的长度,给定下列四组数据,测量时应当用数据( )
A.α,a,b B.α,β,a
C.a,b,γ D.α,β,b
5.有一长为10m的斜坡,倾斜角为,在不改变坡高和坡顶的前提下,要通过加长坡面的方法将它的倾斜角改为,则坡底要延长( )
A.5m B.10m C.m D.m
6.(2017 遂宁模拟改编)海轮“和谐号”从A处以每小时21海里的速度出发,海轮“奋斗号”在A处北偏东45°的方向,且与A相距10海里的C处,沿北偏东105°的方向以每小时9海里的速度行驶,则海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为( )小时。
A. B. C. D.1
填空题
7. 一艘船以的速度向正北方向航行,船在处看见灯塔在船的东北方向上,后船在处看见灯塔在船的北偏东的方向上,这时,船与灯塔的距离 ;
8. (2018 湖北高考)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=_________m.
/
9. 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于 m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,≈1.73)
/
解答题
10.如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时,两船之间的距离最短?
/
11.为保障高考的公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1千米处不能收到手机信号,检查员抽查某市一考点,在考点正西约1.732千米有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以每小时12千米的速度沿公路行驶,问最长需要多少分钟,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
12.一辑私艇发现在北偏东45°方向,距离12海里的海里上有一走私船正以10海里/小时的速度沿南偏东75°方向逃窜,若辑私艇的速度为14海里,辑私艇沿北偏东 的方向追去,若要在最短的时间内追上该走私船,求追及所需的时间和角的正弦值.
13. 如图,A、B是水平面上的两个点,相距800m,在A点测得山顶C的仰角为25°,∠BAD=110°,又在B点测得∠ABD=40°,其中D是点C在水平面上的垂足,求山高CD.(精确到1m)
14.如图,一艘海轮从A出发,沿北偏东的方向航行后到达海岛B,然后从B出发,沿北偏东的方向航行后达到海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?
/
15. 如图所示,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上的一个动点,以PC为边作等边△PCD,且点D与圆心O分别在PC的两侧,求四边形OPDC面积的最大值.
16. (2017 南通模拟)如图,景点A在景点B的正北方向2千米处,景点C在景点D的正东方向千米处。
(1)游客甲沿CA从景点C出发行至景点B相距千米的点P处,记∠PBC=α,求sinα的值;
(2)甲沿CA从景点C出发前往景点A,乙沿AB从景点A出发前往景B,甲乙同时出发,甲的速度为1千米/小时,乙的速度为2千米/小时。若甲乙两人这间通过对讲机联系,对讲机在该景区内的最大通话距离为3千米,问有多长时间两人不能通话?(精确到0.1小时,参考数据:)
/
【答案与解析】
1.答案: A
解析:在△ABC中,AC=50,∠ACB=45°,∠CAB=105°
∴∠ABC=30°,由正弦定理:
∴AB==m.故选A.
2. 答案: D
解析:设AB=x m,则由题意,∠D=30°,∠ACB=45°,
在Rt△ABC中,BC=AB=x,
在Rt△ADB中,DB=CD+BC=100+x,
∴,即,解得。
∴山AB的高度为米。
故选D。
3. 答案:C
解析:如图,
/
由图可知,∠DAB=15°,
∵
在Rt△ADB中,又AD=60,
∴DB=AD?tan15°=60×(2-)=120-60.
在Rt△ADB中,∠DAC=60°,AD=60,
∴DC=AD?tan60°=60.
∴BC=DC-DB=60-(120-60)=120()(m).
∴河流的宽度BC等于120()m.
故选:C.
4. 答案: C
解析: 由A与B不可到达,故不易测量α,β,故选C.
5. 答案: C
解析:在△ABB’中由正弦定理,得
6. 答案: B
解析:设海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为x小时,
/
如图,则由已知得△ABC中,AC=10,AB=21x,BC=9x,∠ACB=120°,
由余弦定理得:(21x)2=100+(9x)2-2×10×9x×cos120°,
整理,得36x2―9x―10=0,
解得或(舍)。
∴海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为小时。
故选:B.
7. 答案:;
如图所示:
/
,,,
在中,根据正弦定理。
8. 答案:/.
解析:
在△ABC中,∠CAB=30°,∠ACB=75°-30°=45°,
根据正弦定理知,,
即,
所以,故应填.
9. 答案:;
解析
过A点作AD垂直于CB的延长线,垂足为D,
则Rt△ACD中,∠C=30°,AD=46m
∴.
又∵Rt△ABD中,∠ABD=67°,可得
∴BC=CD-BD=79.58-19.5=60.08≈60m
故答案为:60m
/
10.解析:设航行x小时后甲船到达C点,乙船到达D点,在△BCD中,BC=(100-50x)海里,BD=30x海里(), ∠CBD=60°,由余弦定理得:
∴当(小时)时,CD2最小,从而得CD最小
∴航行小时,两船之间距离最近.
11.解析: 如图所示,考点为A,检查开始处为B,设公路上C、D两点到考点的距离为1千米.
/
在△ABC中,AB=≈1.732,AC=1,∠ABC=30°,
由正弦定理sin∠ACB=·AB=,
∴∠ACB=120°(∠ACB=60°不合题意),
∴∠BAC=30°,∴BC=AC=1,
在△ACD中,AC=AD,∠ACD=60°,
∴△ACD为等边三角形,∴CD=1.
∵×60=5,∴在BC上需5分钟,CD上需5分钟.
答:最长需要5分钟检查员开始收不到信号,并持续至少5分钟才算合格.
12. 解析:如图所示,A、C分别表示辑私艇,走私船的位置,设经x小时后在B处追上.
则AB=14x,BC=10x,∠ACB=120°
由得x=2.
故AB=28,BC=20
即所需时间2小时,为.
13.
解析:在△ABD中,∠ADB=180°-110°-40°=30°,
由正弦定理得.
在Rt△ACD中,CD=ADtan25°≈480(m).
答:山高约为480m.
14、解析:在中, ,
根据余弦定理,
根据正弦定理, ,
有,
∵ ∴
所以 ,
答:此船应该沿北偏东的方向航行,需要航行
15. 解析:设∠POB=,四边形面积为y,则在△POC中,由余弦定理得:?
PC2=OP2+OC2-2OP·OCcos=5-4cos?
∴y=S△OPC+S△PCD=+(5-4cos)
=2sin(-)+
∴当-=即=时,ymax=2+.
16. 解析:(1)在Rt△ABC中,AB=2,,∴∠C=30°
在△PBC中,由余弦定理得BC2+PC2-2BC·PC·cos30°=BP2,即
化简,得PC2-6PC+5=0,解得PC=1或PC=5(舍去)
在△PBC中,由正弦定理得,即
∴。
(2)Rt△ABC中,BA=2,,
设甲出发后的时间为t小时,则由题意可知0≤t≤4,设甲在线段CA上的位置为点M,AM=4-t
在△PBC中,由余弦定理得BC2+PC2-2BC·PC·cos30°=BP2,
即,化简得PC2-6PC+5=0
解得PC=1或PC=5(舍去)
①当1≤t≤4时,乙在景点B处,甲在线段PA上,甲乙间的距离d≤BP<3,此时不合题意;
②当0≤t<1时,设乙在线段AB上的位置为点Q,则AQ=2t
在△AMQ中,由余弦定理得,MQ2=(4―t)2+(2t)2―2×2t(4-t)×cos60°=7t2-16t+16
令MQ>3即MQ2>9,得7t2-16t+7>0,解得或
∴
综上,当时,甲、乙间的距离大于3米。
又,故两人不能通话的时间大约为0.6小时
