人教A版数学选修2—1 3.1.4 空间向量的正交分解及其坐标表示(共14张ppt)
文档属性
| 名称 | 人教A版数学选修2—1 3.1.4 空间向量的正交分解及其坐标表示(共14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 278.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-15 00:00:00 | ||
图片预览






文档简介
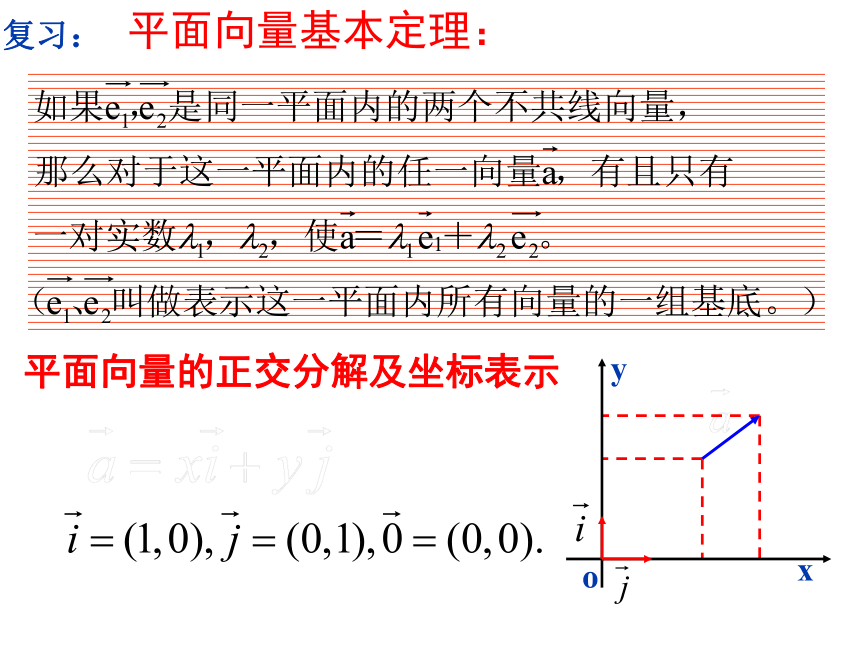
课件14张PPT。3.1.4空间向量的正交 分解及其坐标表示平面向量基本定理:平面向量的正交分解及坐标表示复习:情景引入在上述视频中,一消防官兵特别行动小组接到命令,由此往南500米,再往东400米处的某大厦5楼发生火灾.行动小组迅速赶到现场,经过1个多小时的奋战,终于将大火扑灭.火灾的发源地点是由消防官兵驻地“南500米”“东400米”“5楼”三个量确定.设 是向南的单位向量, 是向东的单位向量, 是向上的单位向量.问题1:这三个向量能作为该空间的一组基底吗?提 示:能.问题2:若每层楼高3米,请把“发生火灾”的位置由向量 表示出来? 提示: =500 +400 +15 .
在空间中,能得出类似的结论:任意不共面的三个向量都可做为空间的一个基底。一、空间向量基本定理: 如果三个向量 不共面,那么对空间任一向量 ,存在一个唯一的有序实数组x,y,z,使都叫做基向量(1)任意不共面的三个向量都可做为空间的一个基底。注:对于基底{a,b,c},除了应知道a,b,c不共面,
还应明确: (2) 由于可视 为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 。(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关连的不同概念。已知空间四边形OABC,其对角线为OB,AC,M,N,分别是对边OA,BC的中点,点P,Q是线段MN三等分点,用基向量OA,OB,OC表示向量OP,OQ.空间向量基本定理的考查例11、已知向量{a,b,c}是空间的一个基底.
求证:向量a+b,a-b,c能构成空间的一个基底.练习 由此可知,如果 是空间两两垂直的向量,那么,对空间任一向量 ,存在一个有序实数组 {x,y,z}使得
我们称 为向量 在
上的分向量。这种分解我们把它叫做空间向量的正交分解.二、空间直角坐标系下空间向量的直角坐标xyzOA(x,y,z)e1e2e3 空间向量的直角坐标: 给定一个空间坐标系和向量 ,且设e1,e2,e3为坐标向量,由空间向量基本定理,存在唯一的有序实数组(x,y, z)使
p = xe1+ye2+ze3
有序数组( x, y, z)叫做p在空间直角坐标系O--xyz中的坐标,记作.P=(x,y,z)其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标.
例2、
1、在空间坐标系o-xyz中, ( 分别是与x轴、 y轴、 z轴的正方向相同的单位向量)则 的坐标为 。
空间直角坐标的考查COBC'AO'B'A'yz2.如图,边长为1的正方体OABC-O’A’B’C’中,
AB’的中点为M,BC’的中点为N,求下列向量
的坐标:MN 1.空间向量基本定理.
在空间,具有大小和方向的量如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.2.基底与基向量.
空间任意三个不共面向量都可以做空间向量的一个基底.一个基底指一个向量组,一个基向量是指基底中的某一个向量.3.空间向量的正交分解.
能从正交基底到空间直角坐标系转换.
在空间中,能得出类似的结论:任意不共面的三个向量都可做为空间的一个基底。一、空间向量基本定理: 如果三个向量 不共面,那么对空间任一向量 ,存在一个唯一的有序实数组x,y,z,使都叫做基向量(1)任意不共面的三个向量都可做为空间的一个基底。注:对于基底{a,b,c},除了应知道a,b,c不共面,
还应明确: (2) 由于可视 为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 。(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关连的不同概念。已知空间四边形OABC,其对角线为OB,AC,M,N,分别是对边OA,BC的中点,点P,Q是线段MN三等分点,用基向量OA,OB,OC表示向量OP,OQ.空间向量基本定理的考查例11、已知向量{a,b,c}是空间的一个基底.
求证:向量a+b,a-b,c能构成空间的一个基底.练习 由此可知,如果 是空间两两垂直的向量,那么,对空间任一向量 ,存在一个有序实数组 {x,y,z}使得
我们称 为向量 在
上的分向量。这种分解我们把它叫做空间向量的正交分解.二、空间直角坐标系下空间向量的直角坐标xyzOA(x,y,z)e1e2e3 空间向量的直角坐标: 给定一个空间坐标系和向量 ,且设e1,e2,e3为坐标向量,由空间向量基本定理,存在唯一的有序实数组(x,y, z)使
p = xe1+ye2+ze3
有序数组( x, y, z)叫做p在空间直角坐标系O--xyz中的坐标,记作.P=(x,y,z)其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标.
例2、
1、在空间坐标系o-xyz中, ( 分别是与x轴、 y轴、 z轴的正方向相同的单位向量)则 的坐标为 。
空间直角坐标的考查COBC'AO'B'A'yz2.如图,边长为1的正方体OABC-O’A’B’C’中,
AB’的中点为M,BC’的中点为N,求下列向量
的坐标:MN 1.空间向量基本定理.
在空间,具有大小和方向的量如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc.2.基底与基向量.
空间任意三个不共面向量都可以做空间向量的一个基底.一个基底指一个向量组,一个基向量是指基底中的某一个向量.3.空间向量的正交分解.
能从正交基底到空间直角坐标系转换.
