人教A版数学选修2—1 1.1.3 四种命题间的相互关系(共20张ppt)
文档属性
| 名称 | 人教A版数学选修2—1 1.1.3 四种命题间的相互关系(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 564.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-15 00:00:00 | ||
图片预览








文档简介
课件20张PPT。四种命题间的相互关系知识回顾交换原命题的条件和结论,所得的命题是________ 。
同时否定原命题的条件和结论,所得的命题是_______。
注意:区分否命题和命题的否定
交换原命题的条件和结论,并且同时否定,所得的命题是__________ 。逆命题否命题逆否命题三个概念否命题是否条件、否结论;而命题的否定是只否结论。
原命题:
逆命题:
否命题:
(命题的否定:
逆否命题:若 p, 则 q
若 q, 则 p
若 ┐p, 则┐q
若 p, 则┐q )
若 ┐q, 则┐p四种命题形式: 路边苦李小故事
古时候有个人叫王戎,7岁那年的某一天和小伙伴在路边玩,看见一棵李子树上的果实多得把树枝都快压断了,小伙伴们都跑去摘,只有王戎站着没动.他说:“李子是苦的,我不吃.”小伙伴摘来一尝,李子果然苦的没法吃.
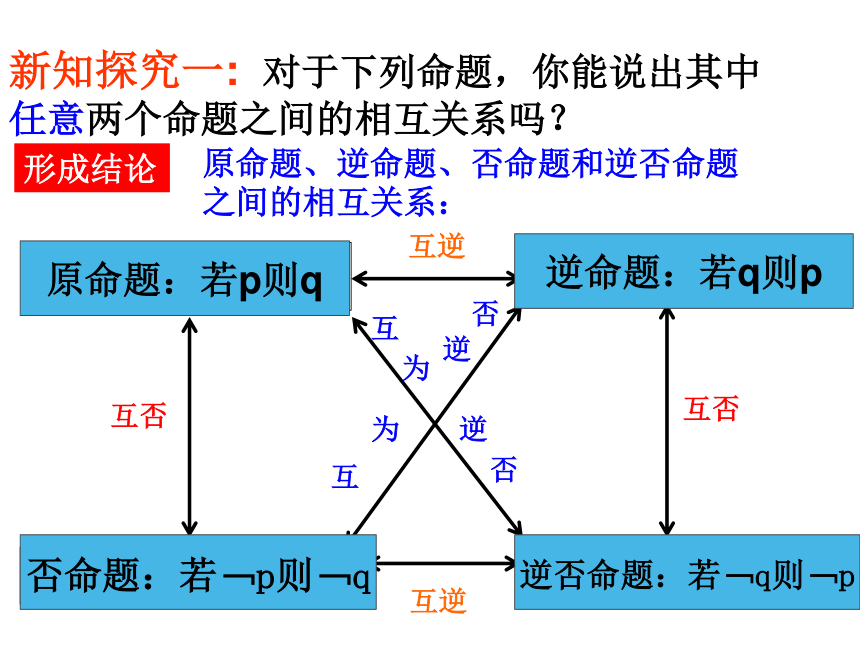
古时候有个人叫王戎,7岁那年的某一天和小伙伴在路边玩,看见一棵李子树上的果实多得把树枝都快压断了,小伙伴们都跑去摘,只有王戎站着没动.他说:“李子是苦的,我不吃.”小伙伴摘来一尝,李子果然苦的没法吃.小伙伴问王戎:“这就怪了!你又没有吃,怎么知道李子是苦的啊?”王戎说:“树长在路边,如果李子不是苦的, 就不会有这么多李子!李子现在还那么多,所以啊,肯定李子是苦的,不好吃!”下面让我们进入今天的学习(1)若a=0,则ab=0.(2)若ab=0,则a=0.(3)若a≠0,则ab≠0.(4)若ab≠0,则a≠0.原命题:若p则q逆命题:若q则p否命题:若﹁p则﹁q逆否命题:若﹁q则﹁p形成结论原命题、逆命题、否命题和逆否命题之间的相互关系:新知探究一: 对于下列命题,你能说出其中
任意两个命题之间的相互关系吗?理论迁移②和③ ①和③ ①和② 若一个四边形是正方形,则它的四条边相等;在下列横线上,填写“互逆”“互否”“互为逆否”
(1)命题:“若q则┐p”与命题“若┐q则p”______
(2)命题:“若┐p则q”与命题“若q则┐p”______
(3)命题:“若┐q则p”与命题“若┐p则q”______
互为逆否 互逆 互否跟踪练习1.若命题p的否命题为q,命题p的逆否命题为r,则q与r的关系是( )
A.互为逆命题 B.互为否命题
C.互为逆否命题 D.以上都不正确解:设命题p为“若m,则n”,则其否命题q是“若¬m,则¬n”;则其逆否命题r是“若¬n,则¬m”;故q与r的的关系是互逆命题。故选A.能力提升以“若x2-3x+2=0,则x=2”为原命题,写出其逆命题,否命题与逆否命题,并判断真假
原命题:若x2-3x+2=0,则x=2;若x=2,则x2-3x+2=0;若x2-3x+2≠0,则x≠2;若x≠2,则x2-3x+2≠0.(假)(假)(真)(真)
思考:四种命题的真假性之间是否有什么规律呢?
新知探究二:逆命题:逆否命题:
否命题:一般的,四种命题的真假性,有且仅有以下 四种情况: 四种命题的真假性之间的关系 两个命题互为逆否命题,它们有相同的真假性;
两个命题为互逆或互否命题,它们的真假性没有 关系。形成结论形成结论四种命题间以及真假的关系:原命题
若p则q逆命题
若q则p否命题
若﹁ p则﹁ q逆否命题
若﹁ q则﹁p互为逆否 同真同假互为逆否 同真同假例2.判断下列说法是否正确。1)一个命题的逆命题为真,它的逆否命题不一定为真。(对)2)一个命题的否命题为真,则原命题一定为假。(错)3)一个命题的原命题为假,它的逆命题一定为假。(错)4)一个命题的逆否命题为假,它的否命题为假。(错)例题讲解如果一个命题的逆命题为假命题,则它的否命题( )
A. 一定是假命题 B.不一定是假命题
C. 一定是真命题 D.有可能是真命题
跟踪练习2AA.①②③④ B.①③④
C.②③④ D.①④
互为逆否命题同真同假的应用例3.B判断命题“已知a,x为实数,若关于x的不等式x2+(2a+1)x+a2+2≤0的解集非空,则a≥1”的逆否命题的真假.等价命题的应用跟踪练习3.法二: 解:原命题的逆否命题是:
已知a,x为实数,若a<1,则关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集.判断其真假如下:
抛物线y=x2+(2a+1)x+a2+2的图象开口向上,
判别式Δ=(2a+1)2-4(a2+2)=4a-7.
因为a<1,所以4a-7<0. Δ<0
所以关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集.
故原命题的逆否命题为真.【提升总结】因为原命题和它的逆否命题有相同的 真假性,所以当直接证明某一命题为真命题有困难 时,可以通过证明它的逆否命题为真命题,来间接证明原命题为真命题.例4. 求证:若 x 2+y 2=0,则x =y =0.不妨设x ≠0,所以x 2+ y 2 >0,也就是说x 2+ y 2 ≠0. 因此,原命题的逆否命题为真命题,从而原命题为真命题.
逆否命题:若x,y不同时为0, 则x2+y2 ≠0若x,y不同时为0,则x,y中至少有一个不为0,证明:则x 2>0,求证:若a2-b2+2a-4b-3 0,则 a-b 1跟踪练习4.这节课你收获了什么?想一想:结合教学目标:
1、这节课我们收获了哪些知识?
2、这节课我们用到了哪些数学方法?
同时否定原命题的条件和结论,所得的命题是_______。
注意:区分否命题和命题的否定
交换原命题的条件和结论,并且同时否定,所得的命题是__________ 。逆命题否命题逆否命题三个概念否命题是否条件、否结论;而命题的否定是只否结论。
原命题:
逆命题:
否命题:
(命题的否定:
逆否命题:若 p, 则 q
若 q, 则 p
若 ┐p, 则┐q
若 p, 则┐q )
若 ┐q, 则┐p四种命题形式: 路边苦李小故事
古时候有个人叫王戎,7岁那年的某一天和小伙伴在路边玩,看见一棵李子树上的果实多得把树枝都快压断了,小伙伴们都跑去摘,只有王戎站着没动.他说:“李子是苦的,我不吃.”小伙伴摘来一尝,李子果然苦的没法吃.
古时候有个人叫王戎,7岁那年的某一天和小伙伴在路边玩,看见一棵李子树上的果实多得把树枝都快压断了,小伙伴们都跑去摘,只有王戎站着没动.他说:“李子是苦的,我不吃.”小伙伴摘来一尝,李子果然苦的没法吃.小伙伴问王戎:“这就怪了!你又没有吃,怎么知道李子是苦的啊?”王戎说:“树长在路边,如果李子不是苦的, 就不会有这么多李子!李子现在还那么多,所以啊,肯定李子是苦的,不好吃!”下面让我们进入今天的学习(1)若a=0,则ab=0.(2)若ab=0,则a=0.(3)若a≠0,则ab≠0.(4)若ab≠0,则a≠0.原命题:若p则q逆命题:若q则p否命题:若﹁p则﹁q逆否命题:若﹁q则﹁p形成结论原命题、逆命题、否命题和逆否命题之间的相互关系:新知探究一: 对于下列命题,你能说出其中
任意两个命题之间的相互关系吗?理论迁移②和③ ①和③ ①和② 若一个四边形是正方形,则它的四条边相等;在下列横线上,填写“互逆”“互否”“互为逆否”
(1)命题:“若q则┐p”与命题“若┐q则p”______
(2)命题:“若┐p则q”与命题“若q则┐p”______
(3)命题:“若┐q则p”与命题“若┐p则q”______
互为逆否 互逆 互否跟踪练习1.若命题p的否命题为q,命题p的逆否命题为r,则q与r的关系是( )
A.互为逆命题 B.互为否命题
C.互为逆否命题 D.以上都不正确解:设命题p为“若m,则n”,则其否命题q是“若¬m,则¬n”;则其逆否命题r是“若¬n,则¬m”;故q与r的的关系是互逆命题。故选A.能力提升以“若x2-3x+2=0,则x=2”为原命题,写出其逆命题,否命题与逆否命题,并判断真假
原命题:若x2-3x+2=0,则x=2;若x=2,则x2-3x+2=0;若x2-3x+2≠0,则x≠2;若x≠2,则x2-3x+2≠0.(假)(假)(真)(真)
思考:四种命题的真假性之间是否有什么规律呢?
新知探究二:逆命题:逆否命题:
否命题:一般的,四种命题的真假性,有且仅有以下 四种情况: 四种命题的真假性之间的关系 两个命题互为逆否命题,它们有相同的真假性;
两个命题为互逆或互否命题,它们的真假性没有 关系。形成结论形成结论四种命题间以及真假的关系:原命题
若p则q逆命题
若q则p否命题
若﹁ p则﹁ q逆否命题
若﹁ q则﹁p互为逆否 同真同假互为逆否 同真同假例2.判断下列说法是否正确。1)一个命题的逆命题为真,它的逆否命题不一定为真。(对)2)一个命题的否命题为真,则原命题一定为假。(错)3)一个命题的原命题为假,它的逆命题一定为假。(错)4)一个命题的逆否命题为假,它的否命题为假。(错)例题讲解如果一个命题的逆命题为假命题,则它的否命题( )
A. 一定是假命题 B.不一定是假命题
C. 一定是真命题 D.有可能是真命题
跟踪练习2AA.①②③④ B.①③④
C.②③④ D.①④
互为逆否命题同真同假的应用例3.B判断命题“已知a,x为实数,若关于x的不等式x2+(2a+1)x+a2+2≤0的解集非空,则a≥1”的逆否命题的真假.等价命题的应用跟踪练习3.法二: 解:原命题的逆否命题是:
已知a,x为实数,若a<1,则关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集.判断其真假如下:
抛物线y=x2+(2a+1)x+a2+2的图象开口向上,
判别式Δ=(2a+1)2-4(a2+2)=4a-7.
因为a<1,所以4a-7<0. Δ<0
所以关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集.
故原命题的逆否命题为真.【提升总结】因为原命题和它的逆否命题有相同的 真假性,所以当直接证明某一命题为真命题有困难 时,可以通过证明它的逆否命题为真命题,来间接证明原命题为真命题.例4. 求证:若 x 2+y 2=0,则x =y =0.不妨设x ≠0,所以x 2+ y 2 >0,也就是说x 2+ y 2 ≠0. 因此,原命题的逆否命题为真命题,从而原命题为真命题.
逆否命题:若x,y不同时为0, 则x2+y2 ≠0若x,y不同时为0,则x,y中至少有一个不为0,证明:则x 2>0,求证:若a2-b2+2a-4b-3 0,则 a-b 1跟踪练习4.这节课你收获了什么?想一想:结合教学目标:
1、这节课我们收获了哪些知识?
2、这节课我们用到了哪些数学方法?
