人教版高中数学必修5同步练习题、期中、期末复习资料、补习资料:24【提高】一元二次不等式
文档属性
| 名称 | 人教版高中数学必修5同步练习题、期中、期末复习资料、补习资料:24【提高】一元二次不等式 |
|
|
| 格式 | zip | ||
| 文件大小 | 419.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-30 00:00:00 | ||
图片预览




文档简介
一元二次不等式及其解法
【学习目标】
1.掌握一元二次不等式的解法,体会数形结合的思想;
2.理解一元二次不等式、一元二次方程与二次函数之间的关系;
3.能利用一元二次不等式解决简单的实际问题.
【要点梳理】
要点一、一元二次不等式及一元二次不等式的解集
只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.比如:.一元二次不等式的一般形式:或.
设一元二次方程的两根为且,则不等式的解集为,不等式的解集为
要点诠释:讨论一元二次不等式或其解法时要保证成立.
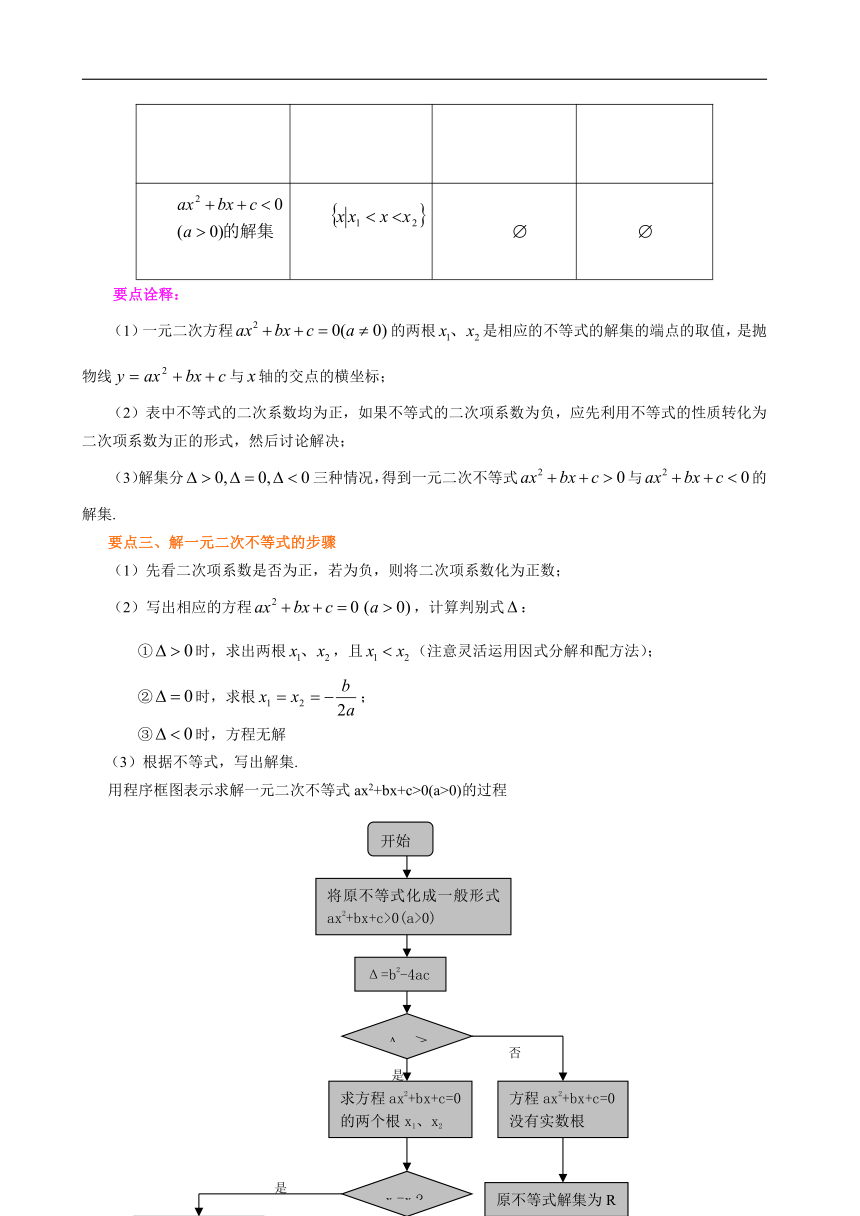
要点二、一元二次不等式与相应函数、方程之间的联系
对于一元二次方程的两根为且,设,它的解按照,,可分三种情况,相应地,二次函数的图像与轴的位置关系也分为三种情况.因此我们分三种情况来讨论一元二次不等式或的解集.
二次函数
()的图象
有两相异实根
有两相等实根
无实根
要点诠释:
(1)一元二次方程的两根是相应的不等式的解集的端点的取值,是抛物线与轴的交点的横坐标;
(2)表中不等式的二次系数均为正,如果不等式的二次项系数为负,应先利用不等式的性质转化为二次项系数为正的形式,然后讨论解决;
(3)解集分三种情况,得到一元二次不等式与的解集.
要点三、解一元二次不等式的步骤
(1)先看二次项系数是否为正,若为负,则将二次项系数化为正数;
(2)写出相应的方程,计算判别式:
①时,求出两根,且(注意灵活运用因式分解和配方法);
②时,求根;
③时,方程无解
(3)根据不等式,写出解集.
用程序框图表示求解一元二次不等式ax2+bx+c>0(a>0)的过程
要点诠释:
1.解一元二次不等式首先要看二次项系数a是否为正;若为负,则将其变为正数;
2.若相应方程有实数根,求根时注意灵活运用因式分解和配方法;
3.写不等式的解集时首先应判断两根的大小,若不能判断两根的大小应分类讨论;
4.根据不等式的解集的端点恰为相应的方程的根,我们可以利用韦达定理,找到不等式的解集与其系数之间的关系;
5.若所给不等式最高项系数含有字母,还需要讨论最高项的系数.
【典型例题】
类型一:一元二次不等式的解法
例1. 解下列一元二次不等式
(1); (2); (3)
【思路点拨】转化为相应的函数,数形结合解决,或利用符号法则解答.
【解析】
(1)方法一:
因为
所以方程的两个实数根为:,
函数的简图为:
/
因而不等式的解集是.
方法二: 或
解得 或 ,即或.
因而不等式的解集是.
(2)方法一:
因为,
方程的解为.
函数的简图为:
/
所以,原不等式的解集是
方法二:(当时,)
所以原不等式的解集是
(3)方法一:
原不等式整理得.
因为,方程无实数解,
函数的简图为:
/
所以不等式的解集是.
所以原不等式的解集是.
方法二:∵
∴原不等式的解集是.
【总结升华】
1. 初学二次不等式的解法应尽量结合二次函数图象来解决,培养并提高数形结合的分析能力;
2. 当时,用配方法,结合符号法则解答比较简洁(如第2、3小题);当且是一个完全平方数时,利用因式分解和符号法则比较快捷,(如第1小题).
3. 当二次项的系数小于0时,一般都转化为大于0后,再解答.
举一反三:
【变式1】已知函数 解不等式f(x)>3.
【答案】由题意知或
解得:x>1.
故原不等式的解集为{x|x>1}.
【变式2】解不等式:
【答案】原不等式可化为不等式组
,即,即,
解得
∴原不等式的解集为.
类型二:含字母系数的一元二次不等式的解法
例2.解关于x的不等式:ax2-x+1>0
【解析】若a=0,原不等式化为-x+1>0,解集为{x|x<1};
若a≠0,原不等式为关于x的一元二次不等式.
方程的判别式△=1-4a
(Ⅰ)当△=1-4a<0,即时,方程没有实数根,
故函数的图象开口向上,与x轴没有交点,其简图如下:
/
所以,此时不等式的解集为实数集R;
(Ⅱ)当△=1-4a=0,即时,方程有两个相等实数根x=2,
故函数的图象开口向上,与x轴有唯一交点(2,0),其简图如下:
/
所以,此时不等式的解集为;
(Ⅲ)当△=1-4a>0,即时,方程有两个不等实数根
,,
①当时,函数的图象开口向上,
与x轴有两个不同的交点,且,其简图如下:
/
所以,此时不等式的解集为;
②当a<0时,函数的图象开口向下,
与x轴有两个不同的交点,且,其简图如下:
/
所以,此时不等式的解集为;
综上所述:
a<0时,原不等式解集为;
a=0时,原不等式解集为;
时,原不等式解集为;
时,原不等式解集为;
时,原不等式解集为实数集R.
【总结升华】对含字母的二元一次不等式,一般有这样几步:
①定号:对二次项系数大于零和小于零分类,确定了二次曲线的开口方向;
②求根:求相应方程的根.当无法判断判别式与0的关系时,要引入讨论,分类求解;
③定解:根据根的情况写出不等式的解集;当无法判断两根的大小时,引入讨论.
举一反三:
【变式1】(2018 天津校级模拟)已知2a+1<0,关于x的不等式的解集是( )
A.{x|x>5a或x<-a} B.{x|-aC. {x|x<5a或x>-a} D.{x|5a 【答案】不等式可化为
(x-5a)(x+a)>0;
∵方程(x-5a)(x+a)的两根为
且2a+1<0,∴a<-,
∴ 5a<-a
∴原不等式的解集为{x|x<5a或x>-a}。
故选C.
【变式2】求不等式12x2-ax>a2(a∈R)的解集.
【答案】
当a>0时,不等式的解集为;
当a=0时,不等式的解集为{x|x∈R且x≠0};
当a<0时,不等式的解集为.
【变式3】(2018秋 太原校级期中)已知集合A={x|x2―2ax―8a2≤0}。
(1)当a=1时,求集合;
(2)若a>0,且,求实数a的取值范围。
【答案】(1)当a=1时,x2―2ax―8a2≤0化为x2―2x―8≤0,
解得:-2≤x≤4。
∴A={x|-2≤x≤4}。
;
(2)由x2―2ax―8a2≤0,且a>0,得-2a≤x≤4a。
∴A={x|-2a≤x≤4a}。
由,得
,解得。
∴实数a的取值范围是。
例3.解关于x的不等式:ax2-(a+1)x+1<0.
【思路点拨】
解不等式时首先应判断两根的大小,若不能判断两根的大小应分类讨论;
【解析】若a=0,原不等式-x+1<0x>1;
若a<0,原不等式或x>1;
若a>0,原不等式,
其解的情况应由与1的大小关系决定,故
(1)当a=1时,原不等式;
(2)当a>1时,原不等式;
(3)当0<a<1时,原不等式
综上所述:
当a<0,解集为;
当a=0时,解集为{x|x>1};
当0<a<1时,解集为;
当a=1时,解集为;
当a>1时,解集为.
【总结升华】熟练掌握一元二次不等式的解法是解不等式的基础,对最高项含有字母系数的不等式,要注意按字母的取值情况进行分类讨论,分类时要“不重不漏”.
举一反三:
【变式1】解关于x的不等式:(ax-1)(x-2)≥0;
【答案】当a=0时,x∈(-(,2].
当a≠0时,方程(ax-1)(x-2)=0两根为
①当a>0时,
若, 即时,;
若, 即时,x∈R;
若, 即时,.
②当a<0时,则有:, ∴ .
【变式2】解关于x的不等式:ax2+2x-1<0;
【答案】当a=0时,.
当a≠0时,Δ=4+4a=4(a+1),
①a>0时,则Δ>0,.
②a<0时,
若a<0,△<0, 即a<-1时,x∈R;
若a<0,△=0, 即a=-1时,x∈R且x≠1;
若a<0,△>0, 即 -1类型三:一元二次不等式的逆向运用
例4. 不等式的解集为,求关于的不等式的解集.
【思路点拨】
由二次不等式的解集为可知:4、5是方程的二根,故由韦达定理可求出、的值,从而解得.
【解析】由题意可知方程的两根为和
由韦达定理有,
∴,
∴化为,即
,解得,
故不等式的解集为.
【总结升华】二次方程的根是二次函数的零点,也是相应的不等式的解集的端点.根据不等式的解集的端点恰为相应的方程的根,我们可以利用韦达定理,找到不等式的解集与其系数之间的关系,这一点是解此类题的关键.
举一反三:
【变式1】(2018 浙江校级模拟)设关于x的不等式(ax-1)(x+1)<0(a∈R)的解集为{x|-1 A.-2 B.-1 C.0 D.1
【答案】∵关于x的不等式(ax-1)(x+1)<0(a∈R)的解集为{x|-1∴对应一元二次方程(ax-1)(x+1)=0的两个实数根为-1和1,
∴或x=-1,
即a的值是1,故选D。
【变式2】已知的解为,试求、,并解不等式.
【答案】由韦达定理有:,,∴,.
∴代入不等式得,
即,,解得,
故不等式的解集为:.
【变式3】已知关于的不等式的解集为,求关于的不等式的解集.
【答案】由韦达定理有:,解得,
代入不等式得
,即,解得或.
∴的解集为:.
类型四:不等式的恒成立问题
例5.已知关于x的不等式(m2+4m-5)x2-4(m-1)x+3>0对一切实数x恒成立,求实数m的取值范围.
【思路点拨】
不等式对一切实数恒成立,即不等式的解集为R,要解决这个问题还需要讨论二次项的系数。
【解析】
(1)当m2+4m-5=0时,m=1或m=-5
若m=1,则不等式化为3>0, 对一切实数x成立,符合题意.
若m=-5,则不等式为24x+3>0,不满足对一切实数x均成立,所以m=-5舍去.
(2)当m2+4m-5≠0即 m≠1且m≠-5时,
由此一元二次不等式的解集为R知,抛物线y=(m2+4m-5)x2-4(m-1)x+3开口向上,且与x轴无交点,
所以,
即, ∴ 1 综上所述,实数m的取值范围是{m|1≤m<19}.
【总结升华】情况(1)是容易忽略的,所以当我们遇到二次项系数含有字母时,一般需讨论.
举一反三:
【变式1】 若关于的不等式的解集为空集,求的取值范围.
【答案】关于的不等式的解集为空集
即的解集为R
当时,原不等式为:,即,不符合题意,舍去.
当时,原不等式为一元二次不等式,只需且,
即,解得,
综上,的取值范围为:.
【变式2】已知不等式ax2+4x+a>1-2x2对一切实数x恒成立,
求实数a的取值范围.
【答案】原不等式等价于(a+2)x2+4x+a-1>0对一切实数恒成立,
显然a=-2时,解集不是R,因此a≠-2,
从而有
整理,得
解得a>2.
故a的取值范围是(2,+∞).
【巩固练习】
一、选择题
1.(2018 四川模拟)若不等式x2+ax+b<0的解集为(―1,2),则ab的值为( )
A.―1 B.1 C.―2 D.2
2.若0<t<1,则不等式的解集为( )
A. B.
C. D.
3.已知不等式ax2-bx-1≥0的解集是,则不等式x2-bx-a<0的解集是( )
A.(2,3) B.(-∞,2)∪(3,+∞)
C. D.
4.在R上定义运算?:x?y=x(1-y).若不等式(x-a)?(x+a)<1对任意实数x恒成立,则( )
A.-1<a<1 B.0<a<2
C. D.
5.不等式x2-ax-b<0的解集是{x|2<x<3},则bx2-ax-1>0的解集是( )
A. B. C. D.
6.(2018 天津校级模拟)设0A. -1二、填空题
7.若函数是定义在(0,+∞)上的增函数,且对一切x>0,y>0都有f(xy)=f(x)+f(y),则不等式f(x+6)+f(x)<2f(4)的解集为________.
8.如果关于x的方程x2-(m-1)x+2-m=0的两根为正实数,则m的取值范围是________.
9.(2018 杭州校级模拟)正实数x,y满足:,则x2+y2-10xy的最小值为________。
10. 已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值是 .
三、解答题
11.解下列不等式
(1)2x2+7x+3>0; (2)-x2+8x-3>0;
12. 不等式mx2+1>mx 的解集为实数集R,求实数m的取值范围.
13. 解关于x的不等式m2x2+2mx-3<0(其中m∈R).
14.已知,
(1)如果对一切x∈R,f(x)>0恒成立,求实数a的取值范围;
(2)如果对x∈[-3,1],f(x)>0恒成立,求实数a的取值范围.
15. 已知a为实数,A为不等式x2-(2a+1)x+(a+2)(a-1)≥0的解集,B为不等式x2-a(a+1)x+a3<0的解集.
(1)用区间表示A和B;
(2)是否存在实数a,使A∪B=R?并证明你的结论.
16. (2018 辽宁)设函数f(x)=2|x-1|+x-1,g(x)=16x2-8x+1.记f(x)≤1的解集为M,g(x)≤4的解集为N.
(Ⅰ)求M;
(Ⅱ)当x∈M∩N时,证明:x2f(x)+x[f(x)]2≤.
【答案与解析】
1.【答案】D
【解析】不等式x2+ax+b<0的解集为(―1,2),
所以方程x2+ax+b=0的实数根为―1和2,
所以,解得a=―1,b=―2,
所以ab=―1×(-2)=2。
故选D。
2.【答案】 D
【解析】 ∵0<t<1,∴,∴
∴.
3. 【答案】 A
【解析】 由题意知,是ax2-bx-1=0的两实根,
∴.解得.
∴x2-bx-a<0?x2-5x+6<0?2<x<3.
4. 【答案】 C
【解析】 因为(x-a)?(x+a)=(x-a)(1-x-a),又不等式(x-a)?(x+a)<1对任意实数x恒成立,所以(x-a)(1-x-a)<1对任意实数x恒成立,即x2-x-a2+a+1>0对任意实数x恒成立,所以Δ=(-1)2-4(-a2+a+1)<0,解得,故选C.
5.【答案】C
【解析】由题意得,方程x2-ax-b=0的两根为x=2,x=3,由韦达定理得,,求得
,从而解得bx2-ax-1>0的解集为
6. 【答案】C
【解析】关于x的不等式,即,∵0[(a+1)x-b][(a-1)x+b]<0的解集中的整数恰有3个,所以a>1,
∴不等式的解集为,所以解集里的整数是-2,-1,0三个。
∴
∴
∵b<1+a, ∴2a-2<1+a, ∴a<3,
综上,17.【答案】 {x|0<x<2}
【解析】 由已知得f(x+6)+f(x)=f[x(x+6)],
2f(4)=f(4)+f(4)=f(4×4)=f(16),
∴原不等式等价于.
8.【答案】
【解析】由题意得:
,解得
9. 【答案】 ―36
【解析】由得x+y=xy,
平方得x2+y2+2xy=(xy)2,
即x2+y2=―2xy+(xy)2,
则x2+y2―10xy=(xy)2―2xy―10xy=(xy)2―12xy=(xy―6)2―36,
当xy=6时,有最小值,即最小值为―36,
故答案为:―36。
10. 【答案】
【解析】∵a+b+c=0,a2+b2+c2=1,
∴b+c=-a,b2+c2=1-a2,
∴bc?(2bc)
[(b+c)2-(b2+c2)]
=a2
∴b、c是方程:x2+ax+a2=0的两个实数根,
∴△≥0
∴a2-4(a2)≥0,即a2≤
∴,即a的最大值为
故答案为:.
11.【解析】
(1)因为Δ=72-4×2×3=25>0,
所以方程2x2+7x+3=0有两个不等实根x1=-3,.
又二次函数y=2x2+7x+3的图象开口向上,
所以原不等式的解集为.
(2)因为Δ=82-4×(-1)×(-3)=52>0,
所以方程-x2+8x-3=0有两个不等实根
,.
又二次函数y=-x2+8x-3的图象开口向下,
所以原不等式的解集为.
12.【答案】{m|0≤m<4}
【解析】
当m=0时,不等式即为1>0,满足条件.
当m≠0时,若不等式的解集为R,则应有, 解得0<m<4.
综上,m的取值范围是{m|0≤m<4}.
13.【解析】 当m=0时,原不等式可化为-3<0,其对一切x∈R都成立,
所以原不等式的解集为R.
当m≠0时,m2>0,
由m2x2+2mx-3<0,得(mx-1)(mx+3)<0,
即,
若m>0,则,
所以原不等式的解集为;
若m<0,则,
所以原不等式的解集为.
综上所述,当m=0时,原不等式的解集为R;
当m>0时,原不等式的解集为;
当m<0时,原不等式的解集为.
14.【解析】
(1)由题意得:△=,即0(2)由x∈[-3,1],f(x)>0得,有如下两种情况:
或
综上所述:.
15. 【解析】 不等式x2-(2a+1)x+(a+2)(a-1)≥0可以转化为[x-(a+2)][x-(a-1)]≥0,不等式x2-a(a+1)x+a3<0可以转化为(x-a)(x-a2)<0.
(1)因为对任意实数a都有a-1<a+2,
所以A=(-∞,a-1]∪[a+2,+∞).
当a2≥a,即a≥1或a≤0时,B=(a,a2);
当a2<a,即0<a<1时,B=(a2,a).
(2)要使A∪B=R,则
当a≥1或a≤0时,需,该不等式组无解;
当0<a<1时,需,该不等式组无解.
所以不存在实数a,使得A∪B=R.
16. 【解析】(Ⅰ)由f(x)=2|x-1|+x-1≤1 可得 ①,或 ②.
解①求得1≤x≤,解②求得 0≤x<1.
综上,原不等式的解集为[0,].
(Ⅱ)由g(x)=16x2-8x+1≤4,求得-≤x≤,∴N=[-,],∴M∩N=[0,].
∵当x∈M∩N时,f(x)=1-x,x2f(x)+x[f(x)]2 =xf(x)[x+f(x)]
=-≤,
故要证的不等式成立.
【学习目标】
1.掌握一元二次不等式的解法,体会数形结合的思想;
2.理解一元二次不等式、一元二次方程与二次函数之间的关系;
3.能利用一元二次不等式解决简单的实际问题.
【要点梳理】
要点一、一元二次不等式及一元二次不等式的解集
只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.比如:.一元二次不等式的一般形式:或.
设一元二次方程的两根为且,则不等式的解集为,不等式的解集为
要点诠释:讨论一元二次不等式或其解法时要保证成立.
要点二、一元二次不等式与相应函数、方程之间的联系
对于一元二次方程的两根为且,设,它的解按照,,可分三种情况,相应地,二次函数的图像与轴的位置关系也分为三种情况.因此我们分三种情况来讨论一元二次不等式或的解集.
二次函数
()的图象
有两相异实根
有两相等实根
无实根
要点诠释:
(1)一元二次方程的两根是相应的不等式的解集的端点的取值,是抛物线与轴的交点的横坐标;
(2)表中不等式的二次系数均为正,如果不等式的二次项系数为负,应先利用不等式的性质转化为二次项系数为正的形式,然后讨论解决;
(3)解集分三种情况,得到一元二次不等式与的解集.
要点三、解一元二次不等式的步骤
(1)先看二次项系数是否为正,若为负,则将二次项系数化为正数;
(2)写出相应的方程,计算判别式:
①时,求出两根,且(注意灵活运用因式分解和配方法);
②时,求根;
③时,方程无解
(3)根据不等式,写出解集.
用程序框图表示求解一元二次不等式ax2+bx+c>0(a>0)的过程
要点诠释:
1.解一元二次不等式首先要看二次项系数a是否为正;若为负,则将其变为正数;
2.若相应方程有实数根,求根时注意灵活运用因式分解和配方法;
3.写不等式的解集时首先应判断两根的大小,若不能判断两根的大小应分类讨论;
4.根据不等式的解集的端点恰为相应的方程的根,我们可以利用韦达定理,找到不等式的解集与其系数之间的关系;
5.若所给不等式最高项系数含有字母,还需要讨论最高项的系数.
【典型例题】
类型一:一元二次不等式的解法
例1. 解下列一元二次不等式
(1); (2); (3)
【思路点拨】转化为相应的函数,数形结合解决,或利用符号法则解答.
【解析】
(1)方法一:
因为
所以方程的两个实数根为:,
函数的简图为:
/
因而不等式的解集是.
方法二: 或
解得 或 ,即或.
因而不等式的解集是.
(2)方法一:
因为,
方程的解为.
函数的简图为:
/
所以,原不等式的解集是
方法二:(当时,)
所以原不等式的解集是
(3)方法一:
原不等式整理得.
因为,方程无实数解,
函数的简图为:
/
所以不等式的解集是.
所以原不等式的解集是.
方法二:∵
∴原不等式的解集是.
【总结升华】
1. 初学二次不等式的解法应尽量结合二次函数图象来解决,培养并提高数形结合的分析能力;
2. 当时,用配方法,结合符号法则解答比较简洁(如第2、3小题);当且是一个完全平方数时,利用因式分解和符号法则比较快捷,(如第1小题).
3. 当二次项的系数小于0时,一般都转化为大于0后,再解答.
举一反三:
【变式1】已知函数 解不等式f(x)>3.
【答案】由题意知或
解得:x>1.
故原不等式的解集为{x|x>1}.
【变式2】解不等式:
【答案】原不等式可化为不等式组
,即,即,
解得
∴原不等式的解集为.
类型二:含字母系数的一元二次不等式的解法
例2.解关于x的不等式:ax2-x+1>0
【解析】若a=0,原不等式化为-x+1>0,解集为{x|x<1};
若a≠0,原不等式为关于x的一元二次不等式.
方程的判别式△=1-4a
(Ⅰ)当△=1-4a<0,即时,方程没有实数根,
故函数的图象开口向上,与x轴没有交点,其简图如下:
/
所以,此时不等式的解集为实数集R;
(Ⅱ)当△=1-4a=0,即时,方程有两个相等实数根x=2,
故函数的图象开口向上,与x轴有唯一交点(2,0),其简图如下:
/
所以,此时不等式的解集为;
(Ⅲ)当△=1-4a>0,即时,方程有两个不等实数根
,,
①当时,函数的图象开口向上,
与x轴有两个不同的交点,且,其简图如下:
/
所以,此时不等式的解集为;
②当a<0时,函数的图象开口向下,
与x轴有两个不同的交点,且,其简图如下:
/
所以,此时不等式的解集为;
综上所述:
a<0时,原不等式解集为;
a=0时,原不等式解集为;
时,原不等式解集为;
时,原不等式解集为;
时,原不等式解集为实数集R.
【总结升华】对含字母的二元一次不等式,一般有这样几步:
①定号:对二次项系数大于零和小于零分类,确定了二次曲线的开口方向;
②求根:求相应方程的根.当无法判断判别式与0的关系时,要引入讨论,分类求解;
③定解:根据根的情况写出不等式的解集;当无法判断两根的大小时,引入讨论.
举一反三:
【变式1】(2018 天津校级模拟)已知2a+1<0,关于x的不等式的解集是( )
A.{x|x>5a或x<-a} B.{x|-a
(x-5a)(x+a)>0;
∵方程(x-5a)(x+a)的两根为
且2a+1<0,∴a<-,
∴ 5a<-a
∴原不等式的解集为{x|x<5a或x>-a}。
故选C.
【变式2】求不等式12x2-ax>a2(a∈R)的解集.
【答案】
当a>0时,不等式的解集为;
当a=0时,不等式的解集为{x|x∈R且x≠0};
当a<0时,不等式的解集为.
【变式3】(2018秋 太原校级期中)已知集合A={x|x2―2ax―8a2≤0}。
(1)当a=1时,求集合;
(2)若a>0,且,求实数a的取值范围。
【答案】(1)当a=1时,x2―2ax―8a2≤0化为x2―2x―8≤0,
解得:-2≤x≤4。
∴A={x|-2≤x≤4}。
;
(2)由x2―2ax―8a2≤0,且a>0,得-2a≤x≤4a。
∴A={x|-2a≤x≤4a}。
由,得
,解得。
∴实数a的取值范围是。
例3.解关于x的不等式:ax2-(a+1)x+1<0.
【思路点拨】
解不等式时首先应判断两根的大小,若不能判断两根的大小应分类讨论;
【解析】若a=0,原不等式-x+1<0x>1;
若a<0,原不等式或x>1;
若a>0,原不等式,
其解的情况应由与1的大小关系决定,故
(1)当a=1时,原不等式;
(2)当a>1时,原不等式;
(3)当0<a<1时,原不等式
综上所述:
当a<0,解集为;
当a=0时,解集为{x|x>1};
当0<a<1时,解集为;
当a=1时,解集为;
当a>1时,解集为.
【总结升华】熟练掌握一元二次不等式的解法是解不等式的基础,对最高项含有字母系数的不等式,要注意按字母的取值情况进行分类讨论,分类时要“不重不漏”.
举一反三:
【变式1】解关于x的不等式:(ax-1)(x-2)≥0;
【答案】当a=0时,x∈(-(,2].
当a≠0时,方程(ax-1)(x-2)=0两根为
①当a>0时,
若, 即时,;
若, 即时,x∈R;
若, 即时,.
②当a<0时,则有:, ∴ .
【变式2】解关于x的不等式:ax2+2x-1<0;
【答案】当a=0时,.
当a≠0时,Δ=4+4a=4(a+1),
①a>0时,则Δ>0,.
②a<0时,
若a<0,△<0, 即a<-1时,x∈R;
若a<0,△=0, 即a=-1时,x∈R且x≠1;
若a<0,△>0, 即 -1
例4. 不等式的解集为,求关于的不等式的解集.
【思路点拨】
由二次不等式的解集为可知:4、5是方程的二根,故由韦达定理可求出、的值,从而解得.
【解析】由题意可知方程的两根为和
由韦达定理有,
∴,
∴化为,即
,解得,
故不等式的解集为.
【总结升华】二次方程的根是二次函数的零点,也是相应的不等式的解集的端点.根据不等式的解集的端点恰为相应的方程的根,我们可以利用韦达定理,找到不等式的解集与其系数之间的关系,这一点是解此类题的关键.
举一反三:
【变式1】(2018 浙江校级模拟)设关于x的不等式(ax-1)(x+1)<0(a∈R)的解集为{x|-1
【答案】∵关于x的不等式(ax-1)(x+1)<0(a∈R)的解集为{x|-1
∴或x=-1,
即a的值是1,故选D。
【变式2】已知的解为,试求、,并解不等式.
【答案】由韦达定理有:,,∴,.
∴代入不等式得,
即,,解得,
故不等式的解集为:.
【变式3】已知关于的不等式的解集为,求关于的不等式的解集.
【答案】由韦达定理有:,解得,
代入不等式得
,即,解得或.
∴的解集为:.
类型四:不等式的恒成立问题
例5.已知关于x的不等式(m2+4m-5)x2-4(m-1)x+3>0对一切实数x恒成立,求实数m的取值范围.
【思路点拨】
不等式对一切实数恒成立,即不等式的解集为R,要解决这个问题还需要讨论二次项的系数。
【解析】
(1)当m2+4m-5=0时,m=1或m=-5
若m=1,则不等式化为3>0, 对一切实数x成立,符合题意.
若m=-5,则不等式为24x+3>0,不满足对一切实数x均成立,所以m=-5舍去.
(2)当m2+4m-5≠0即 m≠1且m≠-5时,
由此一元二次不等式的解集为R知,抛物线y=(m2+4m-5)x2-4(m-1)x+3开口向上,且与x轴无交点,
所以,
即, ∴ 1
【总结升华】情况(1)是容易忽略的,所以当我们遇到二次项系数含有字母时,一般需讨论.
举一反三:
【变式1】 若关于的不等式的解集为空集,求的取值范围.
【答案】关于的不等式的解集为空集
即的解集为R
当时,原不等式为:,即,不符合题意,舍去.
当时,原不等式为一元二次不等式,只需且,
即,解得,
综上,的取值范围为:.
【变式2】已知不等式ax2+4x+a>1-2x2对一切实数x恒成立,
求实数a的取值范围.
【答案】原不等式等价于(a+2)x2+4x+a-1>0对一切实数恒成立,
显然a=-2时,解集不是R,因此a≠-2,
从而有
整理,得
解得a>2.
故a的取值范围是(2,+∞).
【巩固练习】
一、选择题
1.(2018 四川模拟)若不等式x2+ax+b<0的解集为(―1,2),则ab的值为( )
A.―1 B.1 C.―2 D.2
2.若0<t<1,则不等式的解集为( )
A. B.
C. D.
3.已知不等式ax2-bx-1≥0的解集是,则不等式x2-bx-a<0的解集是( )
A.(2,3) B.(-∞,2)∪(3,+∞)
C. D.
4.在R上定义运算?:x?y=x(1-y).若不等式(x-a)?(x+a)<1对任意实数x恒成立,则( )
A.-1<a<1 B.0<a<2
C. D.
5.不等式x2-ax-b<0的解集是{x|2<x<3},则bx2-ax-1>0的解集是( )
A. B. C. D.
6.(2018 天津校级模拟)设0
7.若函数是定义在(0,+∞)上的增函数,且对一切x>0,y>0都有f(xy)=f(x)+f(y),则不等式f(x+6)+f(x)<2f(4)的解集为________.
8.如果关于x的方程x2-(m-1)x+2-m=0的两根为正实数,则m的取值范围是________.
9.(2018 杭州校级模拟)正实数x,y满足:,则x2+y2-10xy的最小值为________。
10. 已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值是 .
三、解答题
11.解下列不等式
(1)2x2+7x+3>0; (2)-x2+8x-3>0;
12. 不等式mx2+1>mx 的解集为实数集R,求实数m的取值范围.
13. 解关于x的不等式m2x2+2mx-3<0(其中m∈R).
14.已知,
(1)如果对一切x∈R,f(x)>0恒成立,求实数a的取值范围;
(2)如果对x∈[-3,1],f(x)>0恒成立,求实数a的取值范围.
15. 已知a为实数,A为不等式x2-(2a+1)x+(a+2)(a-1)≥0的解集,B为不等式x2-a(a+1)x+a3<0的解集.
(1)用区间表示A和B;
(2)是否存在实数a,使A∪B=R?并证明你的结论.
16. (2018 辽宁)设函数f(x)=2|x-1|+x-1,g(x)=16x2-8x+1.记f(x)≤1的解集为M,g(x)≤4的解集为N.
(Ⅰ)求M;
(Ⅱ)当x∈M∩N时,证明:x2f(x)+x[f(x)]2≤.
【答案与解析】
1.【答案】D
【解析】不等式x2+ax+b<0的解集为(―1,2),
所以方程x2+ax+b=0的实数根为―1和2,
所以,解得a=―1,b=―2,
所以ab=―1×(-2)=2。
故选D。
2.【答案】 D
【解析】 ∵0<t<1,∴,∴
∴.
3. 【答案】 A
【解析】 由题意知,是ax2-bx-1=0的两实根,
∴.解得.
∴x2-bx-a<0?x2-5x+6<0?2<x<3.
4. 【答案】 C
【解析】 因为(x-a)?(x+a)=(x-a)(1-x-a),又不等式(x-a)?(x+a)<1对任意实数x恒成立,所以(x-a)(1-x-a)<1对任意实数x恒成立,即x2-x-a2+a+1>0对任意实数x恒成立,所以Δ=(-1)2-4(-a2+a+1)<0,解得,故选C.
5.【答案】C
【解析】由题意得,方程x2-ax-b=0的两根为x=2,x=3,由韦达定理得,,求得
,从而解得bx2-ax-1>0的解集为
6. 【答案】C
【解析】关于x的不等式,即,∵0
∴不等式的解集为,所以解集里的整数是-2,-1,0三个。
∴
∴
∵b<1+a, ∴2a-2<1+a, ∴a<3,
综上,1
【解析】 由已知得f(x+6)+f(x)=f[x(x+6)],
2f(4)=f(4)+f(4)=f(4×4)=f(16),
∴原不等式等价于.
8.【答案】
【解析】由题意得:
,解得
9. 【答案】 ―36
【解析】由得x+y=xy,
平方得x2+y2+2xy=(xy)2,
即x2+y2=―2xy+(xy)2,
则x2+y2―10xy=(xy)2―2xy―10xy=(xy)2―12xy=(xy―6)2―36,
当xy=6时,有最小值,即最小值为―36,
故答案为:―36。
10. 【答案】
【解析】∵a+b+c=0,a2+b2+c2=1,
∴b+c=-a,b2+c2=1-a2,
∴bc?(2bc)
[(b+c)2-(b2+c2)]
=a2
∴b、c是方程:x2+ax+a2=0的两个实数根,
∴△≥0
∴a2-4(a2)≥0,即a2≤
∴,即a的最大值为
故答案为:.
11.【解析】
(1)因为Δ=72-4×2×3=25>0,
所以方程2x2+7x+3=0有两个不等实根x1=-3,.
又二次函数y=2x2+7x+3的图象开口向上,
所以原不等式的解集为.
(2)因为Δ=82-4×(-1)×(-3)=52>0,
所以方程-x2+8x-3=0有两个不等实根
,.
又二次函数y=-x2+8x-3的图象开口向下,
所以原不等式的解集为.
12.【答案】{m|0≤m<4}
【解析】
当m=0时,不等式即为1>0,满足条件.
当m≠0时,若不等式的解集为R,则应有, 解得0<m<4.
综上,m的取值范围是{m|0≤m<4}.
13.【解析】 当m=0时,原不等式可化为-3<0,其对一切x∈R都成立,
所以原不等式的解集为R.
当m≠0时,m2>0,
由m2x2+2mx-3<0,得(mx-1)(mx+3)<0,
即,
若m>0,则,
所以原不等式的解集为;
若m<0,则,
所以原不等式的解集为.
综上所述,当m=0时,原不等式的解集为R;
当m>0时,原不等式的解集为;
当m<0时,原不等式的解集为.
14.【解析】
(1)由题意得:△=,即0
或
综上所述:.
15. 【解析】 不等式x2-(2a+1)x+(a+2)(a-1)≥0可以转化为[x-(a+2)][x-(a-1)]≥0,不等式x2-a(a+1)x+a3<0可以转化为(x-a)(x-a2)<0.
(1)因为对任意实数a都有a-1<a+2,
所以A=(-∞,a-1]∪[a+2,+∞).
当a2≥a,即a≥1或a≤0时,B=(a,a2);
当a2<a,即0<a<1时,B=(a2,a).
(2)要使A∪B=R,则
当a≥1或a≤0时,需,该不等式组无解;
当0<a<1时,需,该不等式组无解.
所以不存在实数a,使得A∪B=R.
16. 【解析】(Ⅰ)由f(x)=2|x-1|+x-1≤1 可得 ①,或 ②.
解①求得1≤x≤,解②求得 0≤x<1.
综上,原不等式的解集为[0,].
(Ⅱ)由g(x)=16x2-8x+1≤4,求得-≤x≤,∴N=[-,],∴M∩N=[0,].
∵当x∈M∩N时,f(x)=1-x,x2f(x)+x[f(x)]2 =xf(x)[x+f(x)]
=-≤,
故要证的不等式成立.
